\(P3379\) 【模板】最近公共祖先(\(LCA\))
\(LCA\)常见的四种求法
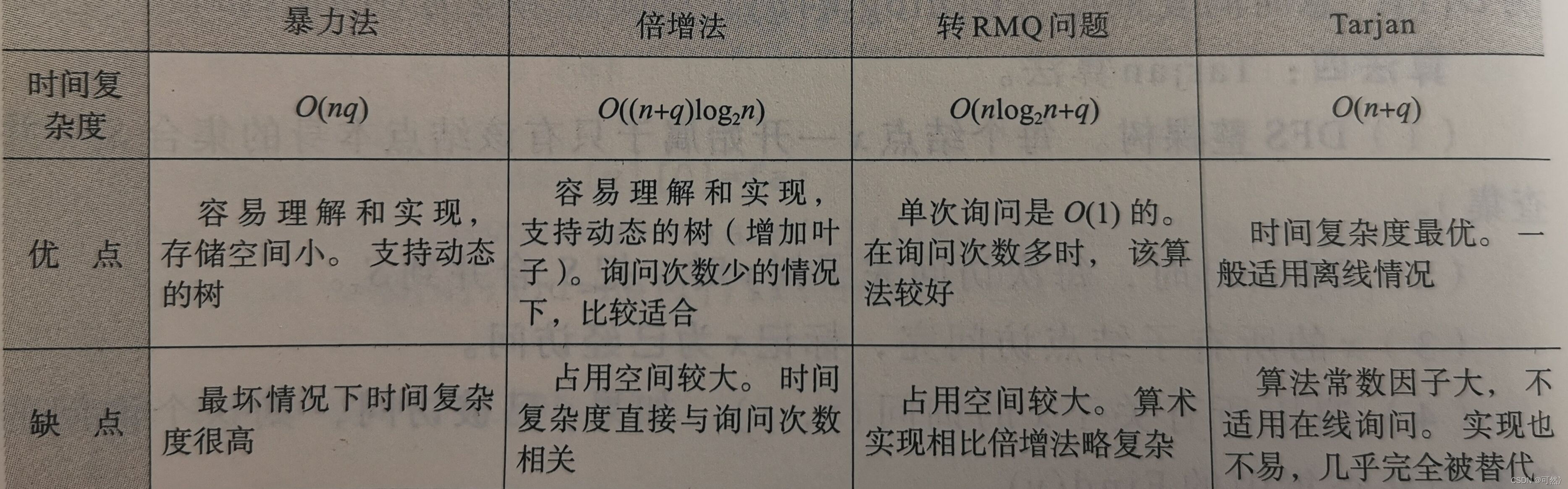
一、暴力
操作步骤:
① 求出每个结点的深度
② 询问两个结点是否重合,若重合,则\(LCA\)已经求出
③ 否则,选择两个点中深度较大的一个,并移动到它的父亲
int depth[N];
int fa[N];
void bfs(int root) {
queue<int> q;
q.push(root);
depth[root] = 1;
fa[root] = -1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!depth[v]) {
depth[v] = depth[u] + 1;
fa[v] = u;
q.push(v);
}
}
}
}
int lca(int a, int b) {
while (a != b) {
if (depth[a] >= depth[b])
a = fa[a];
else
b = fa[b];
}
return a;
}
二、倍增求\(LCA\)
#include <bits/stdc++.h>
using namespace std;
const int N = 500010, M = N << 1;
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
int depth[N];
int f[N][20];
void bfs(int root) {
queue<int> q;
q.push(root);
depth[root] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!depth[v]) {
depth[v] = depth[u] + 1;
f[v][0] = u;
q.push(v);
for (int k = 1; k <= 19; k++) f[v][k] = f[f[v][k - 1]][k - 1];
}
}
}
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int k = 19; k >= 0; k--)
if (depth[f[a][k]] >= depth[b]) a = f[a][k];
if (a == b) return a;
for (int k = 19; k >= 0; k--)
if (f[a][k] != f[b][k])
a = f[a][k], b = f[b][k];
return f[a][0];
}
int main() {
#ifndef ONLINE_JUDGE
freopen("P3379.in", "r", stdin);
#endif
memset(h, -1, sizeof h);
// Q:为什么上面的数组开20,每次k循环到19?
// 答: cout << log2(500000) << endl;
int n, m, s;
scanf("%d %d %d", &n, &m, &s);
int a, b;
for (int i = 1; i < n; i++) {
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
bfs(s);
while (m--) {
scanf("%d %d", &a, &b);
cout << lca(a, b) << endl;
}
return 0;
}
三、\(Tarjan\)算法求\(LCA\)
什么是\(Tarjan\)(离线)算法呢?顾名思义,就是在一次遍历中把所有询问一次性解决,所以其时间复杂度是\(O(n+q)\)。
\(Tarjan\)算法的优点在于 相对稳定,时间 复杂度也比较居中,也很 容易理解。
下面详细介绍一下\(Tarjan\)算法的基本思路:
- 任选一个点为根节点,从根节点开始
- 记\(u\)已被访问过
- 遍历该点\(u\)所有子节点\(j\)
- 若是\(j\)还有子节点,返回\(3\),否则下一步
- 合并\(j\)到\(u\)家族
- 寻找与当前点\(u\)有询问关系的点\(v,id\),
- 若是\(v\)已经被访问过了,\(lca[id]=find(v)\)
遍历的话需要用到\(dfs\)来遍历(我相信来看的人都懂吧...),至于合并,最优化的方式就是利用 并查集 来合并两个节点。
下面上伪代码:
//merge和find为并查集合并函数和查找函数
tarjan(u){
st[u] = true;
for each(u,v){ //访问所有u子节点v
tarjan(v); //继续往下遍历
p[v] = find(u);//合并v到u上
}
for each(u,v){ //访问所有和u有询问关系的v
如果v被访问过;
u,v的最近公共祖先为find(v);
}
}
个人感觉这样还是有很多人不太理解,所以我打算模拟一遍给大家看。
建议拿着纸和笔跟着我的描述一起模拟!!
假设我们有一组数据 \(9\)个节点 \(8\)条边 联通情况如下:
\(1-2,1-3,2-4,2-5,3-6,5-7,5-8,7-9\) 即下图所示的树
设我们要查找最近公共祖先的点为\(9-8,4-6,7-5,5-3\)
设\(f[]\)数组为并查集的父亲节点数组,初始化\(f[i]=i,vis[]\)数组为是否访问过的数组,初始为\(0\);

下面开始模拟过程:
取\(1\)为 根节点,往下搜索 发现有两个儿子\(2\)和\(3\);
先搜\(2\),发现\(2\)有两个儿子\(4\)和\(5\),先搜索\(4\),发现\(4\)没有子节点,则寻找与其有关系的点;
发现\(6\)与\(4\)有关系,但是\(vis[6]=0\),即\(6\)还没被搜过,所以 不操作;
发现没有和\(4\)有询问关系的点了,返回此前一次搜索,更新\(vis[4]=1\);

表示\(4\)已经被搜完,更新\(f[4]=2\),继续搜\(5\),发现\(5\)有两个儿子\(7\)和\(8\);
先搜\(7\),发现\(7\)有一个子节点\(9\),搜索\(9\),发现没有子节点,寻找与其有关系的点;
发现\(8\)和\(9\)有关系,但是\(vis[8]=0\),即\(8\)没被搜到过,所以不操作;
发现没有和\(9\)有询问关系的点了,返回此前一次搜索,更新\(vis[9]=1\);
表示\(9\)已经被搜完,更新\(f[9]=7\),发现\(7\)没有没被搜过的子节点了,寻找与其有关系的点;
发现\(5\)和\(7\)有关系,但是\(vis[5]=0\),所以 不操作;
发现没有和\(7\)有关系的点了,返回此前一次搜索,更新\(vis[7]=1\);

表示\(7\)已经被搜完,更新\(f[7]=5\),继续搜\(8\),发现\(8\)没有子节点,则寻找与其有关系的点;
发现\(9\)与\(8\)有关系,此时\(vis[9]=1\),则他们的最近公共祖先为\(find(9)=5\);
(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)
发现没有与\(8\)有关系的点了,返回此前一次搜索,更新\(vis[8]=1\);
表示\(8\)已经被搜完,更新\(f[8]=5\),发现\(5\)没有没搜过的子节点了,寻找与其有关系的点;

发现\(7\)和\(5\)有关系,此时\(vis[7]=1\),所以他们的最近公共祖先为\(find(7)=5\);
(\(find(7)\)的顺序为f[7]=5-->f[5]=5 return 5;)
又发现\(5\)和\(3\)有关系,但是\(vis[3]=0\),所以不操作,此时\(5\)的子节点全部搜完了;
返回此前一次搜索,更新\(vis[5]=1\),表示\(5\)已经被搜完,更新\(f[5]=2\);
发现\(2\)没有未被搜完的子节点,寻找与其有关系的点;
又发现没有和\(2\)有关系的点,则此前一次搜索,更新\(vis[2]=1\);

表示\(2\)已经被搜完,更新\(f[2]=1\),继续搜\(3\),发现\(3\)有一个子节点\(6\);
搜索\(6\),发现\(6\)没有子节点,则寻找与\(6\)有关系的点,发现\(4\)和\(6\)有关系;
此时\(vis[4]=1\),所以它们的最近公共祖先为\(find(4)=1\);
(\(find(4)\)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)
发现没有与\(6\)有关系的点了,返回此前一次搜索,更新\(vis[6]=1\),表示\(6\)已经被搜完了;

更新\(f[6]=3\),发现\(3\)没有没被搜过的子节点了,则寻找与\(3\)有关系的点;
发现\(5\)和\(3\)有关系,此时\(vis[5]=1\),则它们的最近公共祖先为\(find(5)=1\);
(\(find(5)\)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)
发现没有和\(3\)有关系的点了,返回此前一次搜索,更新\(vis[3]=1\);

更新\(f[3]=1\),发现\(1\)没有被搜过的子节点也没有有关系的点,此时可以退出整个\(dfs\)了。
经过这次\(dfs\)我们得出了所有的答案,有没有觉得很神奇呢?是否对\(Tarjan\)算法有更深层次的理解了呢?
\(Code\)
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 500010, M = N << 1;
//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
vector<PII> query[N]; // query[u]: first:询问的另一个顶点; second:询问的编号
int n, m, s;
int p[N]; // 并查集数组
bool st[N]; // tarjan算法求lca用到的是否完成访问的标识
int lca[N]; // 结果数组
int find(int x) {
if (p[x] != x) p[x] = find(p[x]); //路径压缩
return p[x];
}
void tarjan(int u) {
// ① 标识u已访问
st[u] = true;
//② 枚举u的临边,tarjan没有访问过的点
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!st[j]) {
tarjan(j);
//③ 完成访问后,j点加入u家族
p[j] = u;
}
}
//④ 每个已完成访问的点,记录结果
for (auto q : query[u]) {
int v = q.first, id = q.second;
if (st[v]) lca[id] = find(v);
}
}
int main() {
memset(h, -1, sizeof h);
scanf("%d %d %d", &n, &m, &s);
int a, b;
for (int i = 1; i < n; i++) {
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
for (int i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
query[a].push_back({b, i});
query[b].push_back({a, i});
}
//初始化并查集
for (int i = 1; i <= n; i++) p[i] = i;
tarjan(s);
//输出答案
for (int i = 1; i <= m; i++) printf("%d\n", lca[i]);
return 0;
}
四、RMQ+ST
//3.95s / 227.49MB / 1.67KB C++14 (GCC 9) O2
#include<bits/stdc++.h>
using namespace std;
const int N=500005;
vector<int>vec[N];
//记录每个结点可以走向哪些结点
int f[N*2][21],mem[N*2][21],depth[N*2],first[N],vis[N*2],lg[N];
//f:记录深度序列区间中的最小深度
//mem:记录 找到深度序列区间中的最小深度 时的对应结点(在欧拉序列中)
//depth:在dfs过程中记录遍历到每个点时的对应深度
//first:记录每个结点第一次出现时在欧拉序列中的位置
//vis:欧拉序列
//lg;lg[i]==log_{2}{i}+1
int cnt=0,n,m,s;
//cnt:每走到一个点计一次数
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void dfs(int now,int dep)
{
if(!first[now]) first[now]=++cnt;//第一次遍历到该点
depth[cnt]=dep,vis[cnt]=now;
for(int i=0;i<vec[now].size();i++)
{
if(first[vec[now][i]]) continue;//是该结点的父节点,跳过
else dfs(vec[now][i],dep+1);
++cnt;
depth[cnt]=dep,vis[cnt]=now;//深搜完了vec[now][i]下的分支,回到当前结点 now
}
}
void RMQ()
{
for(int i=1;i<=cnt;i++)
{
lg[i]=lg[i-1]+((1<<lg[i-1])==i);
f[i][0]=depth[i];//区间长度为1时,该区间内深度的最小值就是该结点的深度
mem[i][0]=vis[i];
}
for(int j=1;(1<<j)<=cnt;j++)//枚举的区间长度倍增
for(int i=1;i+(1<<j)-1<=cnt;i++)//枚举合法的每个区间起点
{
if(f[i][j-1]<f[i+(1<<(j-1))][j-1])//深度最小的点在前半个区间
{
f[i][j]=f[i][j-1];
mem[i][j]=mem[i][j-1];
}
else//深度最小的后半个区间
{
f[i][j]=f[i+(1<<(j-1))][j-1];
mem[i][j]=mem[i+(1<<(j-1))][j-1];
}
}
}
int ST(int x,int y)
{
int l=first[x],r=first[y];//找到输入的两个结点编号对应在欧拉序列中第一次出现的位置
if(l>r) swap(l,r);
int k=lg[r-l+1]-1;
if(f[l][k]<f[r-(1<<k)+1][k]) return mem[l][k];
else return mem[r-(1<<k)+1][k];
}
int main()
{
n=read(),m=read(),s=read();
for(int i=1;i<n;i++)
{
int a,b;
a=read(),b=read();
vec[a].push_back(b);
vec[b].push_back(a);
}
dfs(s,0);//打表,给first、depth、vis赋值,给RMQ奠定基础
/*cout<<"各结点第一次出现的位置:"<<endl;
for(int i=1;i<=n;i++)
cout<<first[i]<<' ';
cout<<endl;
cout<<"欧拉序列:"<<endl;
for(int i=1;i<=2*n;i++)
cout<<vis[i]<<' ';
cout<<endl;
cout<<"深度序列"<<endl;
for(int i=1;i<=2*n;i++)
cout<<depth[i]<<' ';
cout<<endl;*/
RMQ();//打表,给f和mem赋值 ,给ST奠定基础
while(m--)
{
int x,y;
x=read(),y=read();
printf("%d\n",ST(x,y));
}
return 0;
}