\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019）]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第二册同步巩固，难度2颗星！

基础知识

基本事实4

(1) 内容
平行与同一条直线的两条直线平行.这性质通常叫做平行线的传递性.
 
(2) 符号表述
\(a || b\) ，\(b || c⟹ a || c\).
 

等角定理

(1) 内容
如果空间中两个角的两条边分别对应平行，那么这两个角相等或互补.
 
(2) 证明
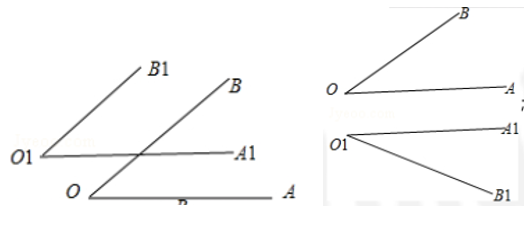
若在空间中，\(AB||A'B'\)，\(AC||A'C'\)，证明在下图\(1\)中\(∠BAC=∠B' A' C'\)，在下图\(2\)中\(∠BAC+∠B' A' C'=180^{\circ}\).

证明 分别在\(∠BAC\)和\(∠B' A' C'\)的两边上截取\(AD\)，\(AE\)和\(AD'\)，\(AE'\)，使得\(AD=A' D'\)，\(AE=A' E'\)，
连接\(AA'\)，\(DD'\)，\(EE'\)，\(DE\)，\(D' E'\)，
\(\because A D \| A^{\prime} D^{\prime}\)，且\(\because A D = A^{\prime} D^{\prime}\)，
\(\therefore\)四边形\(ADD' A'\)是平行四边形，\(\therefore AA'||DD'\)，
同理可证\(AA'||EE'\)，\(\therefore DD'||EE'\)，
\(\therefore\) 四边形\(DD' E' E\)是平行四边形，\(\therefore DE=D' E'\)，
\(\therefore △ADE≅△A' D' E'\)，\(\therefore ∠BAC=∠B' A' C'\).

第二种情况类似证明.
 

基本方法

【题型1】 基本事实4

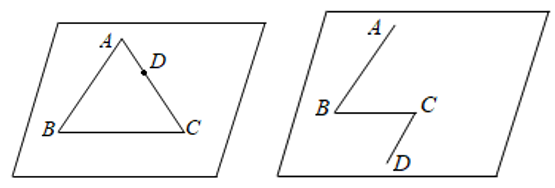
【典题1】如图，空间四边形\(ABCD\)，\(E\)、\(H\)分别是\(AB\)、\(CD\)的中点，\(F\)、\(G\)分别是\(BC\)、\(CD\)上的点，且\(\dfrac{C F}{C B}=\dfrac{C G}{C D}\)，求证: 直线\(EH\)与直线\(FG\)平行.

解析 \(\because E\)、\(H\)分别是\(AB\)、\(CD\)的中点，则\(EH∥BD\)，
\(\because F\)、\(G\)分别是\(BC\)、\(CD\)上的点，且\(\dfrac{C F}{C B}=\dfrac{C G}{C D}\)，\(∠C=∠C\)，
\(\therefore ∆CFG∼∆CBD\)，
\(\therefore ∠CFG=∠CBD\)，\(\therefore FG∥BD\)，
\(\therefore EH∥FG\)，
故直线\(EH\)与直线\(FG\)平行.
点拨
1.通过中位线或相似三角形证明直线平行；
2.通过平行线的传递性证明直线平行，这是一种间接的方法.
 

【巩固练习】

1.若直线\(a∥b\)，\(c\)，\(d\)为不重合的两条直线，且\(a∥c\)，\(b∥d\)，则\(c\)与\(d\)的位置关系是\(\underline{\quad \quad}\) .
 

2.如图，空间四边形\(ABCD\)中，\(E\)，\(F\)，\(G\)，\(H\)分别是\(AB\)，\(BC\)，\(CD\)，\(DA\)的中点．
求证：四边形\(EFGH\)是平行四边形．

 

3.已知棱长为\(a\)的正方体\(ABCD-ABCD'\)中，\(M\)，\(N\)分别为 \(CD\)，\(AD\)的中点.
求证: 四边形\(MNAC\)是梯形.

 

参考答案

1. 答案 平行
   解析 因为\(a∥b\)且\(a∥c\)，
   根据平行线的传递性知\(b\)，\(c\)平行或重合，
   又因为\(b∥d\)，
   再次利用平行线的传递性知\(c\)，\(d\)平行或重合
   因为\(c\)，\(d\)为不重合的两条直线，所以\(c∥d\).

2. 证明 连接\(BD\)，因为\(EH\)是\(△ABD\)的中位线，
   
   所以\(EH∥BD\)，且\(EH=\dfrac{1}{2} BD\)．
   同理\(FG∥BD\)，且\(FG=\dfrac{1}{2} BD\)．
   所以\(EH∥FG\)，且\(EH=FG\)．
   所以四边形\(EFGH\)是平行四边形．

3. 证明 如图所示:
   
   连接\(AC\)，由正方体的性质可知\(AA'=CC'\)，\(AA'∥CC'\)，
   \(\therefore\)四边形\(AA' C' C\)为平行四边形，\(\therefore A' C'=AC\)，\(A' C'∥AC\)，
   又\(\because M\)，\(N\)分别为 \(CD\)，\(AD\)的中点，
   \(\therefore MN∥AC\)，且\(MN=\dfrac{1}{2} AC\)，
   \(\therefore MN∥A' C'\)且\(MN≠A' C'\)，
   \(\therefore\)四边形\(MNA' C'\)是梯形.
    

【题型2】等角定理

【典题1】 如图，\(△ABC\)和\(△A' B' C'\)的对应顶点的连线\(AA'\)，\(BB'\)，\(CC'\)交于同一点\(O\)，且\(\dfrac{A O}{O A^{\prime}}=\dfrac{B O}{O B^{\prime}}=\dfrac{C O}{O C^{\prime}}=\dfrac{2}{3}\).

  (1) 求证:\(A' B' ∥AB\)，\(A' C' ∥AC\)，\(B' C'∥BC\);
  (2) 求\(\dfrac{S_{\triangle A B C}}{S_{\triangle A^{\prime} B^{\prime} C^{\prime}}}\)的值.
解析 (1)\(\because AA'∩BB'=O\)且\(\dfrac{A O}{A^{\prime} O}=\dfrac{B O}{B^{\prime} O}=\dfrac{2}{3}\) ，
\(\therefore AB∥A' B'\)， 同理，\(AC∥A' C'\)，\(BC∥B' C'\) ."
(2)\(A' B'∥AB\)，\(A' C'∥AC\)，
由图知:\(AB\)和\(A' B'\)，\(AC\)和\(A' C\)方向相反，
\(\therefore ∠BAC=∠B' A' C'\)，
同理\(∠ABC=∠A' B' C'\)， \(∠ACB=∠A' C' B'\)，
\(\therefore △ABC∼△A' B' C'\)，
\(\therefore \dfrac{A B}{A^{\prime} B^{\prime}}=\dfrac{A O}{O A^{\prime}}=\dfrac{2}{3}\)，
\(\therefore \dfrac{S_{\triangle A B C}}{S_{\triangle A^{\prime} B^{\prime} C^{\prime}}}=\left(\dfrac{2}{3}\right)^2=\dfrac{4}{9}\).
 

【巩固练习】

1.已知\(∠BAC=30^{\circ}\)，\(AB∥A'B'\)，\(AC∥A'C'\)，则\(∠B'A'C'=\)(　　 )
  A．\(30^{\circ}\) \(\qquad \qquad \qquad \qquad\) B．\(150^{\circ}\) \(\qquad \qquad \qquad \qquad\) C．\(30^{\circ}\)或\(150^{\circ}\) \(\qquad \qquad \qquad \qquad\) D．大小无法确定
 

2.不在同一个平面内的两个三角形的三组对应边分别平行，则这两个三角形 ( )
  A.一定是全等三角形 \(\qquad \qquad\) B.一定是相似但不全等的三角形
  C.一定是相似或全等的三角形 \(\qquad \qquad\) D.可能不全等或相似
 

3.如图，三棱柱\(ABC-A_1 B_1 C_1\)中，\(M\)，\(N\)，\(P\)分别为\(AA_1\)，\(BB_1\)，\(CC_1\)的中点.
求证:\(∠MC_1 N=∠APB\).

 
 

4.长方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(E\)，\(F\)分别为棱\(AA_1\)，\(CC_1\)的中点.

  (1) 求证: \(D_1 E||BF\)；
  (2) 求证: \(∠B_1 BF=∠A_1 ED_1\).
 
 
 

参考答案

1. 答案 \(C\)
   解析 已知\(∠BAC=30^{\circ}\)，\(AB∥A'B'\)，\(AC∥A'C'\)，
   当角的方向相同时，\(∠B' A' C'=30^{\circ}\)，
   当角的方向相反时，\(∠B' A' C'=150^{\circ}\)，
   故选：\(C\)．

2. 答案 \(C\)
   解析 根据等角定理可知，这两个三角形的三个角，分别对应相等，所以这两个三角形一定相似或全等.故选: \(C\).

3. 证明 因为\(N\)，\(P\)分别是 \(BB_1\)，\(CC_1\)的中点，
   所以\(BN||C_1 P\)，\(BN=C_1 P\)，所以四边形\(BPC_1 N\)为平行四边形，所以\(C_1 N||BP\).
   同理可证 \(C_1 M||AP\).
   又 \(∠MC_1 N\)与\(∠APB\)方向相同，所以\(∠MC_1 N=∠APB\).

4. 证明 (1) 如图，取\(BB_1\)的中点\(M\)，连接 \(EM\) ，\(C_1 M\)."
   
   在矩形\(ABB_1 A_1\)中，易得\(EM||A_1 B_1\)，\(EM=A_1 B_1\)，
   因为\(A_1 B_1 ||C_1 D_1\)，\(A_1 B_1=C_1 D_1\)， 所以\(EM||C_1 D_1\)，\(EM=C_1 D_1\)，
   所以四边形\(EMC_1 D_1\)为平行四边形， 所以 \(D_1 E||MC_1\).
   在矩形 \(BCC_1 B_1\)中，易得\(MB||C_1 F\)，\(MB=C_1 F\).
   所以四边形\(MBFC_1\)为平行四边形，
   所以\(BF||MC_1\)， 所以 \(D_1 E||BF\).
   (2) 因为 \(D_1 E||BF\)，\(BB_1 ||EA_1\) ，
   又\(∠B_1 BF\)与\(∠A_1 ED_1\)的对应边方向相同，
   所以\(∠B_1 BF=∠A_1 ED_1\).
    

分层练习

【A组---基础题】

1.已知直线\(a∥\)直线\(b\)，直线\(b∥\)直线\(c\)，直线\(c∥\)直线\(d\)，则\(a\)与\(d\)的位置关系是 ( )
  A.平行 \(\qquad \qquad \qquad\) B.相交 \(\qquad \qquad \qquad\) C. 异面 \(\qquad \qquad \qquad\) D.不确定
 

2.若\(∠AOB=∠A_1 O_1 B_1\)，且\(OA∥O_1 A_1\)，\(OA\)与\(O_1 A_1\)方向相同，则下列结论正确的有( )
  A. \(OB∥O_1 B_1\)且方向相同 \(\qquad \qquad\) B. \(OB∥O_1 B_1\)，方向可能不同
  C. \(OB\)与\(O_1 B_1\)不平行 \(\qquad \qquad\) D. \(OB\)与\(O_1 B_1\)不一定平行
 

3.空间中有三条线段\(AB\)，\(BC\)，\(CD\)，且\(∠ABC=∠BCD\)，那么直线\(AB\)与\(CD\)的位置关系是(　　)
  A．平行 \(\qquad \qquad \qquad\qquad \qquad\) B．异面
  C．相交或平行 \(\qquad \qquad \qquad \qquad\) D．平行或异面或相交均有可能
 

4.(多选)下列命题中，错误的结论有 ( )
  A.如果一个角的两边与另一个角的两边分别平行，那么这两个角相等
  B. 如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角(或直角)相等
  C.如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补
  D.如果两条直线同时平行于第三条直线，那么这两条直线互相平行
 

5.设\(∠A\)与\(∠B\)的两边分别平行，若\(∠A=45^{\circ}\)，则\(∠B\)的大小为\(\underline{\quad \quad}\)．
 

6.对角线互相垂直的空间四边形\(ABCD\)各边中点分别为\(M\)、\(N\)、\(P\)、\(Q\)，则四边形\(MNPQ\)是\(\underline{\quad \quad}\)．
 

7.如图所示，在空间四边形\(ABCD\)中，\(E\)，\(H\)分别为\(AB\)，\(AD\)的中点，\(F\)，\(G\)分别是\(BC\)，\(CD\)上的点，且\(\dfrac{C F}{C B}=\dfrac{C G}{C D}=\dfrac{2}{3}\)，若\(BD=6cm\)，梯形\(EFGH\)的面积为\(28 \mathrm{~cm}^2\)，则平行线\(EH\)，\(FG\)间的距离为\(\underline{\quad \quad}\) .

 

8.如图所示，在三棱柱\(ABC-A_1 B_1 C_1\)中，\(E\)，\(F\)，\(G\)，\(H\)分别是\(AB\)，\(AC\)，\(A_1 B_1\)，\(A_1 C_1\)的中点，求证:\(B\)，\(C\)，\(H\)，\(G\)四点共面.

 

9.在如图所示的正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(E\)，\(F\)，\(E_1\)，\(F_1\)分别是棱\(AB\)，\(AD\)，\(B_1 C_1\)，\(C_1 D_1\)的中点，

求证:(1) \(EF||E_1 F_1\)且\(EF=E_1 F_1\)，\(\qquad \qquad\) (2)\(∠EA_1 F=∠EE_1 CF_1\).
 
 
 

10.如图，在正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(M\)，\(M_1\)分别是棱\(AD\)和\(A_1 D_1\)的中点．

  (1)求证：四边形\(BB_1 M_1 M\)为平行四边形；
  (2)求证：\(∠BMC=∠B_1 M_1 C_1\)．
 
 

参考答案

1. 答案 \(A\)
   解析 \(\because a∥b\)，\(b∥c\)，\(\therefore a∥c\).又\(c∥d\)，\(\therefore a∥d\).故选: \(A\).

2. 答案 \(D\)
   解析 如图，
   
   当\(∠AOB=∠A_1 O_1 B_1\)时，且\(OA∥O_1 A_1\)，\(OA\)与\(O_1 A_1\)的方向相同，\(OB\)与 \(O_1 B_1\)是不一定平行，
   故选: \(D\)

3. 答案 \(D\)
   解析 如图可知\(AB\)，\(CD\)有相交，平行，异面三种情况，
   故选：\(D\)．
   

4. 答案 \(AC\)
   解析 对于选项\(A\)：如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，故选项\(A\)错误；
   对于选项\(B\)：由等角定理可知\(B\)正确；
   对于选项\(C\): 如果一个角的两边和另一个角的两边分别垂直，这两个角的关系不确定，既可能相等也可能互补，也可能既不相等，也不互补.反例如图，在立方体中，\(∠A_1 D_1 C_1\)与\(∠A_1 BC_1\)满足\(A_1 D_1⊥A_1 B\)，\(C_1 D_1⊥C_1 B\)，但是\(\angle A_1 D_1 C_1=\dfrac{\pi}{2}\)，\(\angle A_1 B C_1=\dfrac{\pi}{3}\)，二者不相等也不互补.故选项\(C\)错误.
   
   对于选项\(D\): 如果两条直线同时平行于第三条直线，那么这两条直线平行，故选项\(D\)正确.
   故选:\(AC\).

5. 答案 \(45^{\circ}\)或 \(135^{\circ}\)
   解析 \(\because ∠α\)的两边和\(∠β\)的两边分别平行，
   \(\therefore ∠α\)与\(∠β\)相等或互补，
   \(\because ∠α=45^{\circ}\)，
   \(\therefore ∠β=45^{\circ}\)或\(\angle \beta=180^{\circ}-45^{\circ}=135^{\circ}\).

6. 答案 矩形
   解析 如图所示．
   \(\because\)点\(M\)、\(N\)、\(P\)、\(Q\)分别是四条边的中点，
   \(\therefore MN=\dfrac{1}{2} AC\)且\(MN|| AC\)，\(PQ=\dfrac{1}{2} AC\)且\(PQ||\dfrac{1}{2} AC\)，
   \(\therefore MN=PQ\)且\(MN|| PQ\)，
   \(\therefore\)四边形\(MNPQ\)是平行四边形．
   又\(\because BD∥MQ\)，\(AC⊥BD\)，
   \(\therefore MN⊥MQ\)，\(\therefore\)平行四边形\(MNPQ\)是矩形．
   故答案为：矩形．
   

7. 答案 \(8 cm\)
   解析 \(\because E\)，\(H\)分别为\(AB\)，\(AD\)的中点，\(F\)，\(G\)分别是\(BC\)，\(CD\)上的点，且\(\dfrac{C F}{C B}=\dfrac{C G}{C D}=\dfrac{2}{3}\)，\(BD=6cm\)，
   \(\therefore EH=3\)， \(F G=6 \times \dfrac{2}{3}=4\)
   设\(EH\)，\(FG\)间的距离为\(h\)，
   则 \(S_{\text {梯形 } E F G H^{-}} \dfrac{(E H+F G) h}{2}=28\)，得\(h=8(cm)\)，
   故答案为\(8 cm\).

8. 证明 \(\because G\)，\(H\)分别是\(A_1 B_1\)，\(A_1 C_1\)的中点，
   \(\therefore GH\)是\(△A_1 B_1 C_1\)的中位线，
   \(\therefore GH∥B_1 C_1\)，
   又\(\because B_1 C_1∥BC\)，\(\therefore GH∥B\)C，
   \(\therefore B\)，\(C\)，\(H\)，\(G\)四点共面.

9. 证明 (1)连接\(BD\)，\(B_1 D_1\)，在\(△ABD\)中，
   因为\(E_1\)，\(F\)分别为\(AB\)，\(AD\)的中点，
   所以\(EF=\dfrac{1}{2} BD\)且\(EF|| BD\)，
   同理\(E_1 F_1=\dfrac{1}{2} B_1 D_1\)且\(E_1 F_1|| B_1 D_1\)，
   在正方体\(ABCD-A_1 B_1 C_1 D_1\)中，因为\(AA_1||DD_1\)且\(AA_1=DD_1\)，\(AA_1||BB_1\)且\(AA_1=BB_1\)，
   所以\(B_1 B||DD_1\) 且\(B_1 B=DD_1\)，
   所以四边形\(BDD_1 B_1\)是平行四边形，所以\(BD||B_1 D_1\)且\(BD=B_1 D_1\)，
   所以\(EF||E_1 F_1\)且\(EF=E_1 F_1\).
   (2)取\(A_1 B_1\)的中点\(M\)，连接\(BM\)，\(F_1 M\)，
   因为\(MF_1||B_1 C_1\)且\(MF_1=B_1 C_1\)，\(B_1 C_1||BC\)且\(B_1 C_1=BC\)，
   所以\(MF_1||BC\)且\(MF_1=BC\)，
   所以四边形\(BCF_1 M\)是平行四边形，所以\(MB||CF_1\)，
   因为\(A_1 M||EB\)，所以四边形\(EBMA_1\)是平行四边形，所以\(A_1 E||MB\) ，
   所以\(A_1 E||CF_1\)，
   同理可证:\(A_1 F||E_1 C\)，
   又\(∠EA_1 F\)与\(∠F_1 CE_1\)两边的方向均相反，
   所以\(∠EA_1 F=∠E_1 CF_1\).

10. 证明 (1)在正方形\(ADD_1 A_1\)中，\(M\)，\(M_1\)分别是棱\(AD\)和\(A_1 D_1\)的中点，
    \(\therefore MM_1∥AA_1\)．又\(\because AA_1∥BB_1\)，
    \(\therefore MM_1||BB_1\)，且\(\therefore MM_1=BB_1\)，
    \(\therefore\) 四边形\(BB_1 M_1 M\)为平行四边形．
    (2)由(1)知四边形\(BB_1 M_1 M\)为平行四边形，\(\therefore B_1 M_1∥BM\)．
    同理可得四边形\(CC_1 M_1 M\)为平行四边形，\(\therefore C_1 M_1∥CM\)．
    由平面几何知识可知，\(∠BMC\)和\(∠B_1 M_1 C_1\)都是锐角，
    \(\therefore ∠BMC=∠B_1 M_1 C_1\)．

本栏目推荐文章
• c++ opencv直线检测
• 求空间直线与平面的交点
• 定点、定值、定直线，"三定"问题的灵魂
• 计算两竖直直线与椭圆围成部分面积
• 直线系方程
• 直线和圆的方程
• 【Python】【OpenCV】检测直线和圆
• 交点 - 射线与线段交点 - 直线方程方式
• 如何在latex画直线
• 经典的圆上的点到直线距离为定值的个数问题

直线直线css 直线opencv 方程 直线 点到 直线 坐标 点到 直线 直线canvas 交点 公式 直线 代码 直线 实例 电机maxwell 直线latex 交点 直线cgal