第二章:矢量
矢量(Vector)是用于构建2D和3D属性的正式数学单元。单词Vector有两个不同但相关的含义,在线性代数中,Vector被称为“向量”,而在几何中,Vector被称为“矢量”。
1. 向量和其他无聊东西的数学定义
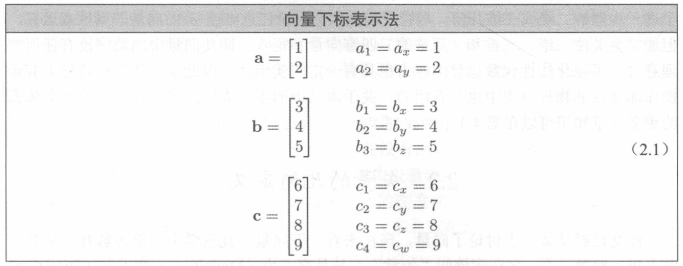
在数学上,向量只不过是一个数字的数组。向量的维度表示包含的向量的数量,它可以是任何正维度。标量也可以被认为是一维的向量。
主要处理向量和矩阵的数学分支称为线性代数,对于3D数学,我们主要关注向量和向量运算的几何解释。
2. 矢量的几何定义
从几何学上讲,矢量是具有大小和方向的有向线段。
矢量的大小是指矢量的长度,矢量可以具有任何非负长度。
矢量的方向描述矢量在空间指向的方向。
矢量可以用来描述相对位置,但矢量本身没有位置,可以在选择任何地方的图形上表示它们,只要正确表示其长度和方向即可。

3. 使用笛卡尔坐标指定矢量
对于任何给定的矢量维度,都有一个特殊的矢量,称为零矢量。它是唯一一个大小为零且没有方向的矢量。我们将零矢量描绘为点,但不要因此把它看作一个“点”。“点”有一个位置但没有实际的尺寸或厚度,因此,“点”和“矢量”具有不同的目的。概念上,“点”指定的是位置,而“矢量”指定的是位移。

4. 相对位置
当提到相对位置,自然而然就会引出一个问题:那“绝对位置”是什么?但其实,并不存在这个东西,我们总要在某些参考系下讨论位置。所幸,绝对位置并不重要,就像我们也不知道自己在宇宙中的确切位置。
由此可得,任何指定位置的方法都必须是相对的,点也是相对的,这样我们就可以推导出点和矢量之间的关系:矢量\(\begin{bmatrix}x,y\end{bmatrix}\)给出了从原点到点\(\begin{pmatrix}x,y\end{pmatrix}\)的位移。
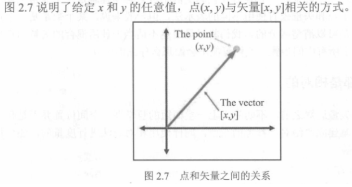
点和矢量在概念上是不同的,而在数学上是等价的,注意不要混淆。
5. 负矢量
让任何维度地矢量变负,可以简单地让矢量的每个分量变负。

矢量变负会产生大小相同但方向相反的矢量。
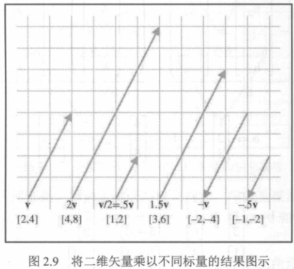
6. 标量和矢量的乘法
矢量与标量相乘,只要简单地用标量乘上矢量的每个分量即可。
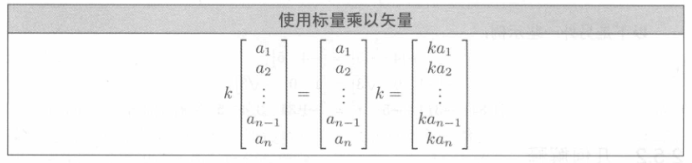
矢量也可以除以非零标量,相当于乘上标量的倒数。

几何解释:将矢量乘上标量\(k\)具有将长度缩放\(\begin{vmatrix}k\end{vmatrix}\)因子的效果。
7. 矢量的加法和减法
只要两个矢量具有相同的维度,就可以进行相加。加法的规则:只要使用它们相应的分量相加即可。

矢量的减法可以理解为加上一个负矢量。
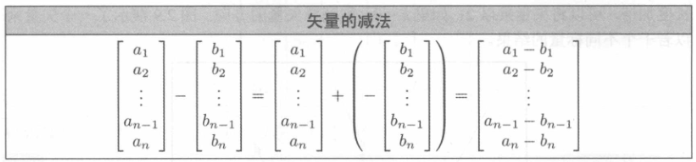
几何解释:矢量加法的三角形法则。
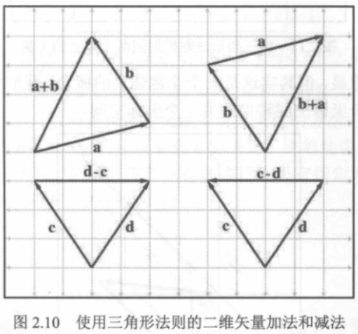
矢量减法 \(b-a\) 产生的是从\(a\)到\(b\)的矢量。
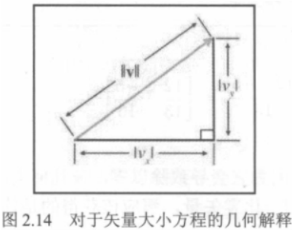
8. 矢量大小
矢量中没有明确表示大小(例如二维矢量\(\begin{pmatrix}3,4\end{pmatrix}\)的大小既不是3也不是4,而是5),所以我们必须计算它。矢量的大小也称为矢量的长度或范数。矢量的大小是矢量分量的平方和的平方根。

几何解释:位移的直线长度
9. 单位矢量
单位矢量,也称为归一化矢量,是大小为1的矢量。当我们只关注矢量的方向而不是大小时,用它就很方便。
对于任何非零矢量\(v\),可以计算指向与\(v\)相同方向的单位矢量,此过程被称为矢量的归一化。

以二维矢量为例,看看归一化的几何解释:
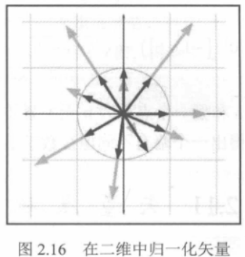
10. 距离公式
两点之间的距离将等于从一点到另一点的矢量的长度。以三维为例:

11. 矢量点积
矢量之间也能进行乘法,而且有两种类型的乘法:一种是点积,也称为内积;另一种是乘积,也称为叉积。
点积在从图形、模拟到AI的各个方面都很有用。此外,点积与许多其他运算具有重要关系,例如矩阵乘法、信号卷积、统计相关和傅里叶变化(心跳骤停)。
“点积”的名称来自矢量乘积表示法中使用的点符号:\(\vec{a}·\vec{b}\),在执行矢量点积运算时,不能再像标量相乘那样省略了。
两个矢量的点积是相应分量的乘积之和,得到的是一个标量。矢量点积是可以交换的:\(\vec{a}·\vec{b} = \vec{b}·\vec{a}\)

现在来讨论点积的更重要的方面:几何意义。它几乎是3D数学的每个方面的基础。
- 点积可以作为投影: 点积\(\vec{a}·\vec{b}\) 等于\(\vec{b}\) 投影到平行于 \(\vec{a}\) 的任何线上的有符号长度,再乘上\(\vec{a}\)的长度。(如果想知道为什么,可以看看这个视频)
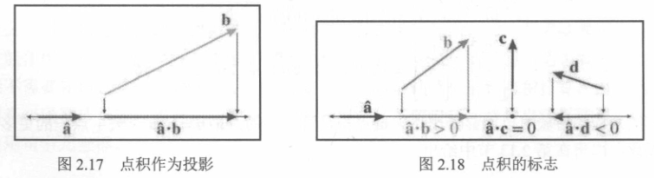
点积的结果是标量,但其符号可以给予我们对两个矢量的相对方向的粗略分类。

点积作为投影的一个常见用法是将矢量分成与另一个矢量平行和垂直的分量。假设 \(\hat{x}\) 作为单位矢量,而 \(\vec{b}\) 具有任意长度,使用点积,可以将\(\vec{b}\)分为\(\vec{b}_{||}\)和\(\vec{b}_{⊥}\),使得\(\vec{b}=\vec{b}_{||}+\vec{b}_{⊥}\)

- 点积与截取角度的关系:两个矢量\(\vec{a}\)和\(\vec{b}\)的点积等于矢量之间角度\(\theta\)的余弦,乘上矢量的长度:\(\vec{a}·\vec{b}=\|\vec{a}\|\|\vec{b}\|\cos\theta\)
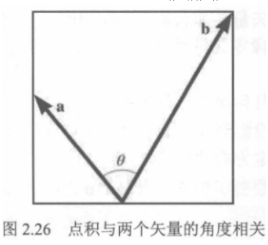
通过反三角函数也很容易求得\(\theta\),如果只需要\(\vec{a}\)和\(\vec{b}\)的相对方向的分类,那么只需要点积的符号即可,这和第一点几何意义中提到的相同。

12. 矢量叉积
叉积只能再三维中应用(作者原话啊)。与点积类似,它的名字来自于表达式:\(\vec{a}\times\vec{b}\),同样叉乘符号不能省略。与点积不同的是,叉积没有交换律,也没有结合律。
叉积与点积具有相同的运算符优先级:乘法发生在加减法之前。当点积与叉积一起使用时,叉积优先(不优先就没法算了):\(\vec{a}·\vec{b}\times\vec{c}=\vec{a}·(\vec{b}\times\vec{c})\)。这种运算也被称为三重积。
叉积将产生一个垂直于原始两个矢量的矢量,计算公式:
叉积的最重要用途之一是创建一个垂直于平面的矢量。
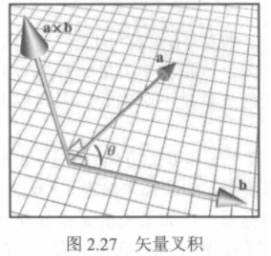
叉积结果矢量的大小等于由两个矢量形成的平行四边形面积。(很容易证明,就不赘述了)

至于叉积的方向,要根据所对应的坐标系是左手还是右手,而用对应的手来比划。梦回高中物理课的安培定则