根号算法

文章内容多摘自 Alex_wei 、 不分解的AgOH 以及 Pecco

一、根号分治

介绍

根号分治是一种分类讨论的思想。对于一个规模为 \(x\) 的问题，如果我们能在 \(O(x)\) 和 \(O(\frac{n}{x})\) 的时间内解决，可以考虑根号分治：当 \(x\leq \sqrt n\) 的时候采用 \(O(x)\) 的算法，\(x > \sqrt n\) 的时候采用 \(O(\frac{n}{x})\) 的算法。这样的时间复杂度是 \(O(q\sqrt n)\) 的，\(q\) 是询问组数。

对于大多数题目而言，一般的步骤是这样：对于暴力能在 \(O(\sqrt n)\) 时间解决的询问，直接用暴力解决，对于不能的问题，考虑通过一些复杂度不超过 \(O(n\sqrt n)\) 的 预处理 来\(O(1)\) 回答询问。

例题

CF797E Array Queries

P3396 哈希冲突

二、分块

块！

介绍

分块其实也是一种思想，把一个整体划分成若干个小块，对于整块打标记，对于零散块单独处理。而利用这个思想处理区间问题的其中一个数据结构就是 块状数组。

块状数组把一个长度为 \(n\) 的序列分成 \(a\) 块，每块的长度为 \(\frac{n}{a}\) 。对于一次区间操作，对区间内部的整块进行整体操作，对区间边缘的零散块单独暴力处理。

要分成多少个块呢？如果块数太少，区间中整块的数量太少，需要暴力处理离散块的时间就多，时间复杂度不能承受；如果块数太多，块长太短，那就失去整体处理的意义。类似于根号分治的，我们取块数为 \(\sqrt n\) ，这样在最坏的情况下，我们要处理 \(\sqrt n\) 个整块和长度为 \(\frac{2n}{\sqrt n}\) 的离散块进行处理。总时间复杂度是 \(O(q\sqrt n)\) 的，这是一种 根号算法。具体就是这个口诀

算法流程

预处理

这里以数列分块入门4为例

给出一个长为 \(n\) 的数列，以及 \(n\) 个操作，操作涉及区间加法，区间求和。

首先划分出每个块的占地范围，由于序列长度可能不是一个完全平方数，那么最后有一小块会漏掉，把这一块纳入最后一块即可。

s = sqrt(n);
for(re int i=1;i<=s;i++)
{
	st[i] = n / s * (i-1) + 1;//每个块的初始位置
	ed[i] = n / s * i;//每个块的终止位置
}
ed[s] = n;

之后，我们为每个元素确定所属块

for(re int i=1;i<=s;i++)
	for(re int j=st[i];j<=ed[i];j++)
		block[j] = i;//下标为j的元素属于第i块

以上是每个分块题都需要预处理的部分，另外不同的题可能还要预处理每个块的大小，块内排序等等信息。

在上文预处理的基础上，这个题中我们还要预处理出 sum 数组表示第 \(i\) 块的和，siz 数组表示每个块的长度。

for(re int i=1;i<=s;i++)
{
	siz[i] = ed[i] - st[i] + 1;
	for(re int j=st[i];j<=ed[i];j++)
		block[j] = i , sum[i] += a[j];
}

区间修改

秉持着 散块打暴力，整块上标记的思想。对于 \(x,y\) 在同一块的时候，因为块长小于 \(\sqrt n\) ，所以直接暴力。

if(block[x] == block[y])
{
	for(re int i=x;i<=y;i++)
	{
		a[i] += k;
		sum[block[i]] += k;
	}
}

对于 \(x,y\) 不在同一个区间的情况，我们先对左右两个零散块暴力处理，对于整块打标记。

for(re int i=x;i<=ed[block[x]];i++)
{
	a[i] += k;
	sum[block[i]] += k;
}
for(re int i=st[block[y]];i<=y;i++)
{
	a[i] += k;
	sum[block[i]] += k;
}
for(re int i=block[x]+1;i<=block[y]-1;i++) tag[i] += k;

区间查询

类似。对于 \(x,y\) 在同一块的时候，直接暴力。

if(block[x] == block[y])
{
	for(re int i=x;i<=y;i++) 
		ans += a[i] + tag[block[i]];//别忘了标记
}

对于 \(x,y\) 不在同一个区间的情况，还是先对左右两个零散块暴力求和，然后对于整块利用乘法结合律快速求解。

for(re int i=x;i<=ed[block[x]];i++) 
	ans += a[i] + tag[block[i]];
for(re int i=st[block[y]];i<=y;i++) 
	ans += a[i] + tag[block[i]];
for(re int i=block[x]+1;i<=block[y]-1;i++) ans += sum[i] + tag[i] * siz[i];
			

以上就是分块解决问题的普遍思路，最关键的还是这个 散块暴力，整块标记的思想。

例题

LOJ分块入门九题

洛谷题单

三、莫队

介绍

莫队算法是一种可以解决大部分区间离线问题的 离线算法 ，它的主要思想基于分块。所以时间复杂度也是 \(O(n \sqrt n)\) 的，虽然有可能会被卡，但是它好写啊。

莫队算法是对 询问 进行分块，所以题目必须可以离线，像蒲公英那样强制在线的就只能用分块或其他算法解决了。

1.普通莫队.

算法思想

先把所有询问的 \([l,r]\) 读入，然后把这些询问按照左端点进行排序,然后分成 \(\sqrt n\) 块。在每一个块的内部再按照右端点进行排序。

如此，我们可以得出：相邻两个询问的左端点变化在 \(\sqrt n\) 以内，而右端点是单调的。我们以上一次询问的回答为基础，那么每个块内只需要花费 \(O(\sqrt n)\) 的费用移动左端点，而整块中右端点增长的范围之和为 \(O(n)\) ，所以在 \(O(n\sqrt n)\) 的范围内解决问题。

简而言之，对于 \(L\) ，在每个块内变 \(\sqrt n\) ，一共跨过 \(\sqrt n\) 个块，所以变化的复杂度是 \(O(n)\) 的；对于 \(R\) ，在每个块内变 \(n\) ，一共跨过 \(\sqrt n\) 个块，所以变化的复杂度是 \(O(n\sqrt n)\) 的。综上，时间复杂度就是 \(O(n\sqrt n)\) 的。

实际上，莫队也是一种暴力，只不过它通过减少左右指针的移动次数，实现了复杂度上的优化。

算法流程

以SP3267 D-Query为例。

首先如上文所说，给询问分块后排序。

int n,q,s,res;
int a[N],t[N];
int st[SqrtN],ed[SqrtN],block[N],ans[N];
struct node{
	int l,r,id;
}p[N];

il bool cmp(node a,node b)
{
	if(block[a.l] == block[b.l]) return a.r < b.r;
	else return a.l < b.l;//上文提到的排序方式
}

il void init()
{
	s = sqrt(n);
	for(re int i=1;i<=s;i++)
	{
		st[i] = n / s * (i-1) + 1;
		ed[i] = n / s * i;
	}
	ed[s] = n;
	for(re int i=1;i<=s;i++)
		for(re int j=st[i];j<=ed[i];j++)
			block[j] = i;
	sort(p+1,p+q+1,cmp);
}

signed main()
{
	n = read() , q = read();
	for(re int i=1;i<=n;i++) a[i] = read();
	for(re int i=1;i<=q;i++) p[i] = (node){read(),read(),i};//离线处理
	init();
}

然后，遍历所有答案，取值。

int l = 1 , r = 0;
for(re int i=1;i<=q;i++)
{
	while(p[i].l < l) Add(--l);//移动左右指针，在移动的同时计算贡献
	while(p[i].r > r) Add(++r);
	while(p[i].l > l) Del(l++);
	while(p[i].r < r) Del(r--);
	ans[p[i].id] = res;
}
for(re int i=1;i<=q;i++) cout << ans[i] << "\n";
	

其中 Add 和 Del 函数就是每个分块题的不同之处。你需要根据不同的题目条件从而 \(O(1)\) 的计算出移动指针产生的贡献，这个题中 Add 和 Del 函数如下：

il void Add(int x)
{
	x = a[x];//t数组就相当于一个桶
	if(t[x] == 0) res++;//没出现过，答案++
	t[x]++;
}

il void Del(int x)
{
	x = a[x];
	if(t[x] == 1) res--;//这个数删去后区间里就没这个数了，答案--
	t[x]--;
}

这个题的 Add 和 Del 函数还是蛮好理解的。但是别的题就不一定了，这两个函数的灵活性十分之高，需要根据不同题目来书写。

一个常数优化：奇偶性优化

代码是这样的

il bool cmp(node a,node b)
{
	return (block[a.l] ^ block[b.l]) ? a.l < b.l : (block[a.l]&1) ? a.r < b.r : a.r > b.r;
}

什么意思呢？对于不同块，还是按照左端点排序；对于同块，如果是奇数块，将右端点从小到大排序，如果是偶数块，将右端点从大到小排序。这实际上就是让右指针的变化能从大到小从小到大的连起来，减少变换次数。实测能优化 \(25\%\) 左右。

莫队和值域分块结合

首先来道例题。P4867

给定一个长度为 \(n\) 的序列 \(a_1,a_2,\dots,a_n\)，\(m\) 次询问 \(l,r,a,b\) ,每次输出 \(a_l - a_r\) 中，权值 \(\in[a,b]\) 的种类数。

如果单纯的用莫队，我们很难在一个可接受的复杂度内去处理区间内的跟权值有关的问题。这就要上我们的值域分块了。

值域分块，顾名思义，把值域进行分块。给定一个 sum[i] 数组，表示在当前这个\([l,r]\)区间内,第 \(i\) 个块所代表的值域中的数出现的个数。显然插入是 \(O(1)\) ，查询是 \(O(\sqrt n)\) 的，这样我们就能在 \(O(n\sqrt m+m\sqrt n)\) 的时间复杂度内解决此题了。其中\(n\sqrt m\) 是莫队的复杂度，\(m\sqrt n\) 是值域分块的复杂度。

有些时候值域可能是 \(10^9\) ,那就先离散化再进行分块。

code:

#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e5 + 5;
const int M = 1e6 + 5;
const int SqrtN = 316 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

//分块复杂度是O(nsqrtm)的，值域分块离散化后每次的复杂度是O(msqrtn)的，总的加起来就是O(nsqrtm+msqrtn)

int a[N],block[N],st[SqrtN],ed[SqrtN],sum[SqrtN],cnt[N];
int n,m,s;
struct node{
	int l,r,a,b,id;
}p[M]; int ans[M];

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

il bool cmp(node a,node b)
{
	return (block[a.l] ^ block[b.l]) ? a.l < b.l : (block[a.l]&1) ? a.r < b.r : a.r > b.r; 
}

il void init()
{
	s = sqrt(n);
	for(re int i=1;i<=s;i++)
	{
		st[i] = n / s * (i-1) + 1;
		ed[i] = n / s * i;
	}
	ed[s] = n;
	for(re int i=1;i<=s;i++)
		for(re int j=st[i];j<=ed[i];j++)
			block[j] = i;
	sort(p+1,p+m+1,cmp);
}

il void Add(int x)
{//在O(1)修改贡献的时候顺便统计sum数组
	cnt[x]++;
	if(cnt[x] == 1) sum[block[x]]++;
}

il void Del(int x)
{
	cnt[x]--;
	if(cnt[x] == 0) sum[block[x]]--;
}

il int Query(int x,int y)
{
	int res = 0;
	if(block[x] == block[y])
	{
		for(re int i=x;i<=y;i++)
			res += (cnt[i] > 0);//散块就判断cnt数组是否大于0即可
	}
	else
	{
		for(re int i=x;i<=ed[block[x]];i++) res += (cnt[i] > 0);
		for(re int i=st[block[y]];i<=y;i++) res += (cnt[i] > 0);
		for(re int i=block[x]+1;i<=block[y]-1;i++) res += sum[i];//整块加sum[i]
	}
	return res;
}

signed main()
{
	n = read() , m = read();
	for(re int i=1;i<=n;i++) a[i] = read();
	for(re int i=1;i<=m;i++) p[i] = (node){read(),read(),read(),read(),i};
	init();
	int l = 1 , r = 0;
	for(re int i=1;i<=m;i++)
	{
		while(p[i].l < l) Add(a[--l]);
		while(p[i].r > r) Add(a[++r]);
		while(p[i].l > l) Del(a[l++]);
		while(p[i].r < r) Del(a[r--]);//前面是莫队
		ans[p[i].id] = Query(p[i].a,p[i].b);//分块sqrtn查询
	}
	for(re int i=1;i<=m;i++) cout << ans[i] << "\n";
	return 0;
}

2.带修莫队

介绍

带修莫队，顾名思义，就是有修改操作的莫队。莫队虽然不能解决强制在线的问题，但是对于有修改操作的离线问题，还是绰绰有余的。

算法思想

带修莫队其实就是在普通莫队每次查询的 \((l,r)\) 二元组的基础上再加上一个时间轴 \(t\) ，构成一个三元组 \((l,r,t)\) ，表示在查询 \([l,r]\) 前进行了 \(t(1 \leq t \leq q)\) 次修改操作。这就相当于是把询问分成了一个个版本。所以每次计算贡献的时候，还要考虑版本的不同，如果不同，就要补上更换版本的贡献。

算法流程

首先和普通莫队不同的是它的排序方式，按以下步骤进行。

• 按左端点 \(L\) 排序，如果 \(L\) 同块，再按 \(R\) 排序；如果 \(R\) 同块，再按 \(t\) 排序。

这样就能尽量减少三个指针的移动次数。

il bool cmp(node a,node b)
{
	if(block[a.l] != block[b.l]) return a.l < b.l;
	if(block[a.r] != block[b.r]) return a.r < b.r;
	return a.ver < b.ver;
}

其次是块的大小，对于带修莫队，块长一般是 \(n^{\frac{2}{3}}\) ，具体证明在这，此时莫队的时间复杂度是 \(O(n^{\frac{5}{3}})\)。

再有就是指针的移动，这里以数颜色这道题为例。

通常 \(t\) 指针的移动是放在 \(l,r\) 指针之后的，change 操作就是用来计算更换版本得到的贡献的，这里有一个很巧妙的点：对于一次版本的更改，我这一次把颜色 \(A\) 改为了 \(B\)，那么可能后续操作还要再改回来，也就是把 \(B\) 改为 \(A\) ，所以每次版本更改直接交换两种颜色就好

il void Change(int tim,int id)
{//c[i].pos代表第i次修改操作修改的位置,c[i].val则表示修改成啥了
	if(q[id].l <= c[tim].pos && c[tim].pos <= q[id].r)//判断这次修改会不会对答案产生贡献
	{
		if(--cnt[a[c[tim].pos]] == 0) res--;
		if(++cnt[c[tim].val] == 1) res++;
	}
	swap(a[c[tim].pos],c[tim].val);//无论产不产生贡献，都要swap
}

for(re int i=1;i<=qnum;i++)
{
	while(q[i].l < l) Add(a[--l]);
	while(q[i].r > r) Add(a[++r]);
	while(q[i].l > l) Del(a[l++]);
	while(q[i].r < r) Del(a[r--]);
	while(t < q[i].ver) Change(++t,i);
	while(t > q[i].ver) Change(t--,i);
	ans[q[i].id] = res;
}

这就是带修莫队相较于普通莫队的更改之处，其实没啥大变化，就是处理了版本对于答案的影响而已。

3.树上莫队

介绍

树上莫队，无非就是把序列问题搬到了树上。所以我们要做的就是再把它给搬回到序列上(。

算法思想&流程

怎么搬呢？两种方法，适用于不同情况。

首先引入两个定义：dfs序和欧拉序。

dfs序：每个节点在 dfs 中的进栈的时间序列。

欧拉序：每个节点在 dfs 中的进栈和出栈的时间序列。

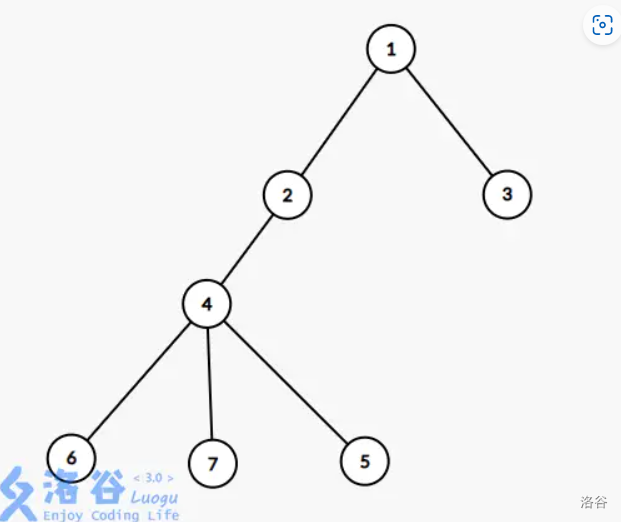
(by eee_hoho)

这个图中以 \(1\) 为根，dfs序为 (1,2,4,6,7,5,3)，欧拉序为 (1,2,4,6,6,7,7,5,5,4,2,3,3,1)。可见，欧拉序的长度是点数的两倍。

求链贡献

对于链的贡献，我们一般用欧拉序来解决，设 \(st_i\) 表示 \(i\) 点入栈的时间戳，\(ed_i\) 表示 \(i\) 点出栈的时间戳。每次询问链 \((u,v)\) 的贡献(u的深度小于v的深度，如果不的话swap一下)。

• 若 \(LCA(u,v) = u\) ，则拿出 \(st_u\) 和 \(st_v\) 之间的区间。比如 \(u=2,v=7\) ，那么 \(st_2-st_7\) 的序列就为 \(2,4,6,6,7\) ，我们可以看到，对于点 \(6\) ,在欧拉序中出现了两次，说明其不属于入栈后就又退出了，所以它不属于这个链。因此我们在统计的时候忽略出现 \(2\) 次的点的贡献。最终统计的就是 \(2,4,7\)。

  为什么？因为 \(v\) 在 \(u\) 的子树之中，要想从 \(u\) 遍历到 \(v\) 肯定已经走过了 \(u\) 和 \(v\) 之间的点，而要想记录这些点的贡献，就不能让欧拉序走到它们回退的时候，所以到 \(st_v\) 终止即可，保证每个点的贡献都能计算到。

• 若 \(LCA(u,v) \not= u\) , 说明 \(v\) 不在 \(u\) 的子树中。这时候我们拿出 \(ed_u - st_v\) 这一段序列即可。比如 \(u=4,v=3\) ，那么 \(ed_4-st_3\) 的序列就为 \(4,2,3\)。最终统计的就是 \(4,2,3\)。

  为什么？因为从 \(ed_u\) 开始，往后的就是 \(u\) 所在的子树回退的过程和进入其他子树的过程,就能保证 \(u\) 到根上的点只出现一次；到 \(st_v\) 结束就能保证从根到 \(v\) 上的点只出现一次。但是我们发现，\(LCA\) 的贡献没有计算，因为 \(LCA\) 的进入时间早于 \(ed_u\) , 而退回时间又晚于 \(st_v\) ，因此需要加上贡献后统计答案。而又因为我们统计的这段序列中，\(LCA\) 的贡献其实是多加进来的，所以要在下次计算贡献之前再把它的贡献减去。

• 由上边我们可以知道，我们需要求得 \(LCA\) ,这里我用倍增做的，在预处理的同时处理欧拉序。

• 如何忽略出现两次的点的贡献：我们给一个标记 \(used_i\) ,如果 \(used_i\) 为 \(1\) ，表明出现过一次了，这次需要减去贡献；反之，加上它的贡献。求完后 used[i] ^= 1 即可。

• 分块的时候大小是 \(2n\) ，因为欧拉序的长度是 \(2n\) 。

核心代码：

il bool cmp(node a,node b)
{
	return (a.l/blo ^ b.l/blo) ? a.l < b.l : ((a.l/blo)&1) ? a.r < b.r : a.r > b.r; 
}

il void dfs(int x,int fa)
{
	f[x][0] = fa , dep[x] = dep[fa] + 1;
	st[x] = ++tot , s[tot] = x;//记录st和ed数组以及记录欧拉序中的每个位置代表的哪个数
	for(re int i=head[x];i;i=edge[i].next)
	{
		int y = edge[i].v;
		if(y == fa) continue;
		dfs(y,x);
	}
	ed[x] = ++tot , s[tot] = x;
}

il void init()//预处理倍增数组

il int LCA(int x,int y)//倍增求LCA

il void Add(int x)//O(1)修改

il void Del(int x)//O(1)修改

il void calc(int x)
{
	used[x] ? Del(a[x]) : Add(a[x]);
	used[x] ^= 1;
}

int main()
{
	//一大堆读入
	for(re int i=1;i<=m;i++)
	{
		u = read() , v = read();
		if(st[u] > st[v]) swap(u,v);//保证u深度较小
		int lca = LCA(u,v);//l,r,lca,id
		if(u == lca) q[i] = (node){st[u],st[v],0,i};//第一种情况
		else q[i] = (node){ed[u],st[v],lca,i};//第二种情况
	}
	sort(q+1,q+m+1,cmp);
	int l = 1 , r = 0;
	for(re int i=1;i<=m;i++)
	{//因为l，r是在欧拉序上移动，而计算贡献要的是欧拉序上这个点的贡献，这就是s数组的意义
		while(l > q[i].l) calc(s[--l]);
		while(r < q[i].r) calc(s[++r]);
		while(l < q[i].l) calc(s[l++]);
		while(r > q[i].r) calc(s[r--]);
		if(q[i].lca) calc(q[i].lca);//看看是否是第二种情况
		ans[q[i].id] = res;
		if(q[i].lca) calc(q[i].lca);
	}
}

求子树贡献

因为 dfs序 有着很好的性质：一段子树内dfs序连续，所以我们计算子树贡献不必用欧拉序，直接记录 dfs 序就行了。在 dfs 中稍微改变一下即可。计算的时候也就用不上 \(used\) 数组了

il void dfs(int x,int fa)
{
	st[x] = ++tot , s[tot] = x;
	for(re int i=head[x];i;i=edge[i].next)
	{
		int y = edge[i].v;
		if(y == fa) continue;
		dfs(y,x);
	}
	ed[x] = tot;//这次dfs走完后，tot就是这棵子树最后一个点的时间戳
}
int main()
{
	for(re int i=1;i<=m;i++)
	{
		while(l > q[i].l) Add(s[--l]);
		while(r < q[i].r) Add(s[++r]);
		while(l < q[i].l) Del(s[l++]);
		while(r > q[i].r) Del(s[r--]);
		//记录答案
	}
}

和带修莫队结合

其实也没啥区别，就是这俩板子掺和在一起，无非就是加了个时间维度更麻烦了(。还要注意块长。

例:SP32952，P4074

和值域分块结合

也是跟普通莫队结合值域分块一样的。只不过码量++。

例：CF1479D

和带修莫队+值域分块结合

码码码！P4175

4.回滚莫队

介绍

回滚莫队用于解决一些插入好更新贡献，而删除不好更新贡献的题目。它的基本思路就是把删除变成插入。

算法思想

回滚莫队是以普通莫队的排序方式解决问题的。
对于右端点，我们在每一个块内可以保证递增，所以贡献计算容易。而对于左端点，则不能保证是单调的了，这样难免会出现删除操作，怎么办呢？

对于这一个块内的操作，我们把初始的 \(l\) 指针放在它下一个块的初始位置，这样每次询问的时候，左端点都是向左拓展的，这样就巧妙的化删除为插入。等到这一个块内操作处理完了，要到下一个块的时候，\(l\) 指针再设到下下个块的初始位置，以此类推。这就是回滚莫队的主要思想。

回滚莫队中的信息分文两种：临时信息和永久信息。对于一个块内的操作，\(l\) 每次都要向左拓展，这些拓展的区域称为临时信息，这些信息只适用于一次询问，询问后就要清空；而 \(r\) 指针在一个块内单调递增，所以它存储的是永久信息，这些信息适用于一个块内的询问，等到 \(l\) 指针移动到下一个块的时候，再在线性的时间内把永久信息删除。

算法流程

给个图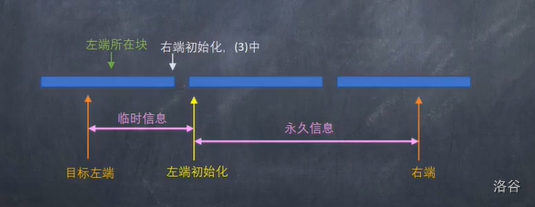 by 电音抖腿不能改

• 1. 首先，按照普通莫队的排序方式排好序，由于算法本身的原因，不能用奇偶性优化。
• 2. 如果当前询问 \(l\) 和 \(r\) 指针在同一块内，暴力回答即可。
• 3. 如果这次的询问和 \(l\) 在同一块内，证明 \(l\) 得往右跨一个块了。我们清空永久信息，移动 \(l\) 指针
• 4. 右端向右移动，更新永久信息
• 5. 左端向左移动，更新临时信息，将临时信息和永久信息合并得到结果。

考虑复杂度：对于 \(l\) ，每次最多移动 \(\sqrt n\) 次，一共要跨 \(\sqrt n\) 个块，复杂度 \(O(n)\) ；对于 \(r\) ,在一个块内更新贡献和最后删除永久信息都是 \(O(n)\) 的，一共要跨 \(\sqrt n\) 个块，复杂度 \(O(n\sqrt n)\) 。综上，回滚莫队的时间复杂度还是熟悉的 \(O(n\sqrt n)\)。

以 歴史の研究一题为例，我们用 \(cnt_i\) 和 \(tempcnt_i\) 分别存储永久信息和临时信息中 \(i\) 的出现个数，最后计算的时候将二者加起来乘以原数得到答案。

il void brute_force(int x,int y,int id)
{
	tempMax = 0;
	for(re int i=x;i<=y;i++) tempcnt[a[i]]++;
	for(re int i=x;i<=y;i++) tempMax = max(tempMax,num[i]*tempcnt[a[i]]);
	ans[id] = tempMax;
	for(re int i=x;i<=y;i++) tempcnt[a[i]]--;
	return ;
}

signed main()
{
	//一堆预处理
	for(re int i=1;i<=m;i++)
	{
	  if(block[q[i].l] == block[q[i].r]) 
     {
        brute_force(q[i].l,q[i].r,q[i].id); 
        continue; 
     }//步骤二
	  if(block[q[i].l]+1 != lastblock)//lastblock表示l指针所在的块
	  {
			Max = 0 , lastblock = block[q[i].l] + 1;
			memset(cnt , 0 , sizeof cnt);//步骤三
			l = st[lastblock] , r = l-1;
		}
		while(r < q[i].r) Add(++r);//步骤4
		tempMax = Max;
		for(re int j=q[i].l;j<=l-1;j++)
		{
			tempcnt[a[j]]++;
			tempMax = max(tempMax,(tempcnt[a[j]]+cnt[a[j]])*num[j]);
		}//步骤五
		for(re int j=q[i].l;j<=l-1;j++) tempcnt[a[j]] = 0;//清空临时信息
		ans[q[i].id] = tempMax;
	}

总结

根号类的算法是一些比较暴力的算法，但是它好写啊。以上的东西基本上包含了分块和莫队的全部算法。当然莫队还有二次离线等神仙操作，等以后水平上来了再去学习。

本栏目推荐文章
• 2024/1/13 算法笔记
• Openharmony 跑 CV 算法
• .NET中的加密算法总结(自定义加密Helper类续)
• 算法练习题
• 算法学习Day26组合总和、分割回文串
• （坚持每天写算法）基础算法复习与学习part1基础算法1-7——高精度减法（处理t=1和t>1代码的写法，t为操作次数）
• 【SPFA】最短路的一种算法
• 基于融合语义信息改进的内容推荐算法。Improved content recommendation algorithm integrating semantic information.
• 秦九韶算法学习笔记
• [RFC6238] TOTP: 基于时间的一次性密码生成算法

根号 算法根号 算法 笔记 根号 算法 根号 根号 函数 个数 根号 做法 根号 积分 数学2023 根号 做法335f abc 根号remainder problem 根号sugoroku 335f abc 根号lt ab