题目
题目描述
在一个圆形操场的四周摆放 \(N\) 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 \(2\) 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 \(N\) 堆石子合并成 \(1\) 堆的最小得分和最大得分。
输入格式
数据的第 \(1\) 行是正整数 \(N\),表示有 \(N\) 堆石子。
第 \(2\) 行有 \(N\) 个整数,第 \(i\) 个整数 \(a_i\) 表示第 \(i\) 堆石子的个数。
输出格式
输出共 \(2\) 行,第 \(1\) 行为最小得分,第 \(2\) 行为最大得分。
样例 #1
样例输入 #1
4 4 5 9 4样例输出 #1
43 54提示
\(1\leq N\leq 100\),\(0\leq a_i\leq 20\)。
解题思路
这是一道区间\(dp\)的模板题(好像所有人接触到区间dp都是通过这一道题的吧)
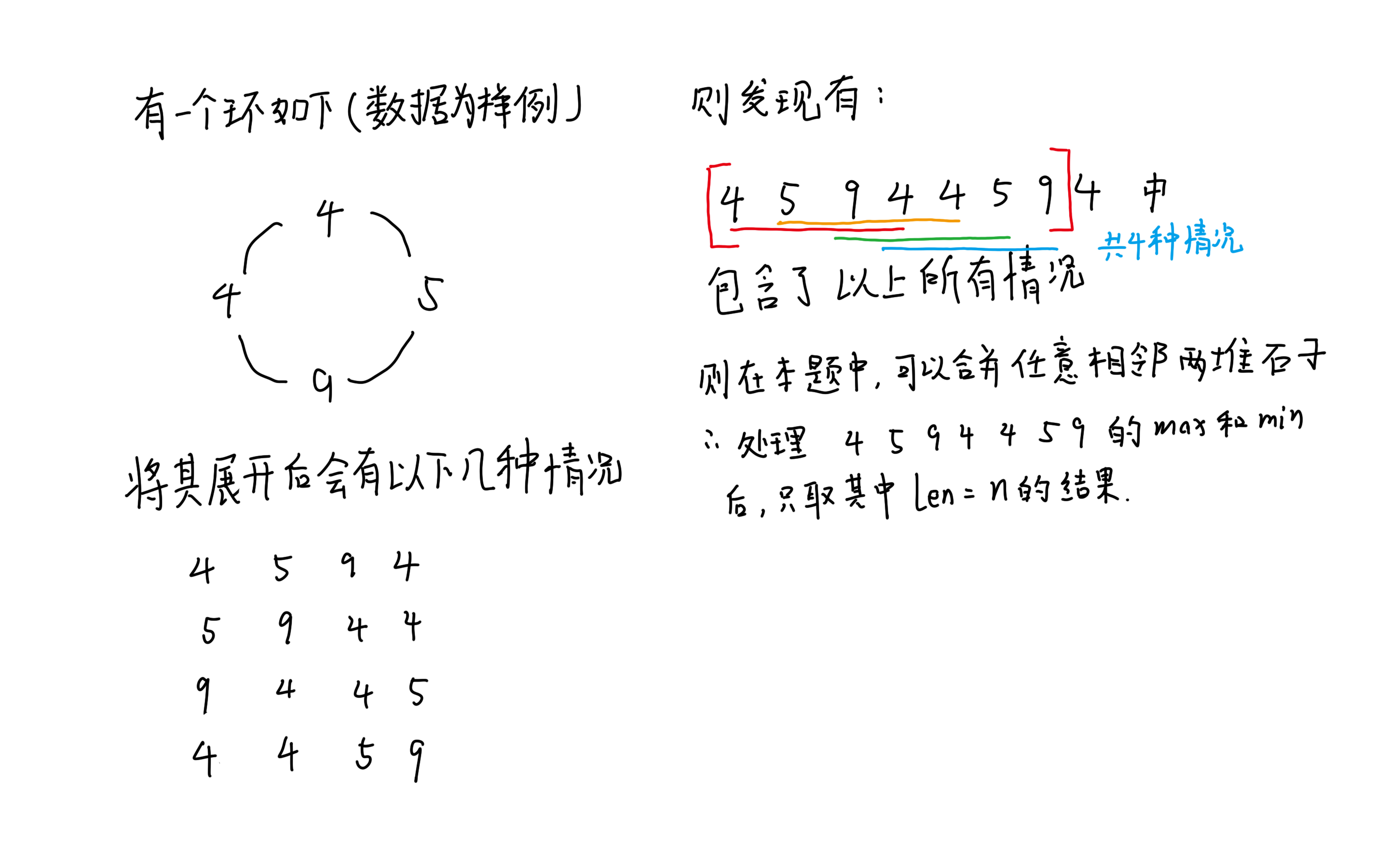
关于\(n\)堆石子围成一个环
关于环的基本解决方法无非就是两种,第一种就是将环展开后复制一遍并接到原来的后面,第二种则是用指针或数据结构直接模拟环。当然,最简单的办法还是第一种。
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
a[n+i]=a[i];//将环展开并且复制一遍
}
for(int i=1;i<=2*n;i++){
sum[i]=sum[i-1]+a[i];//求前缀和
}
求合并所产生的最大值
为什么是动态规划
合并石子的过程当我们把它展开成为一条链以后,就变成了求所有长度为\(n\)的石子堆合并后能够产生的最大值,而每一段石子都是由两堆合并而来的(相当于两段石子)。很明显,这样的子段具有重叠性(子问题的重叠性),就不能够用分治的思想来做了(子问题重叠后用搜索会重复经过某一个状态,导致时间复杂度很大)。(当然记忆化搜索也可以)
而同时这个问题也具备最优子结构的特性,就是当某一段和其他段合并时,无论得到的结果是否是最终的最优结果,就当前来说,这一段的最优值就是这一次合并后的最优值。
很显然,这个问题也没有后效性,求解这一段的最优解并不会影响其他结果。
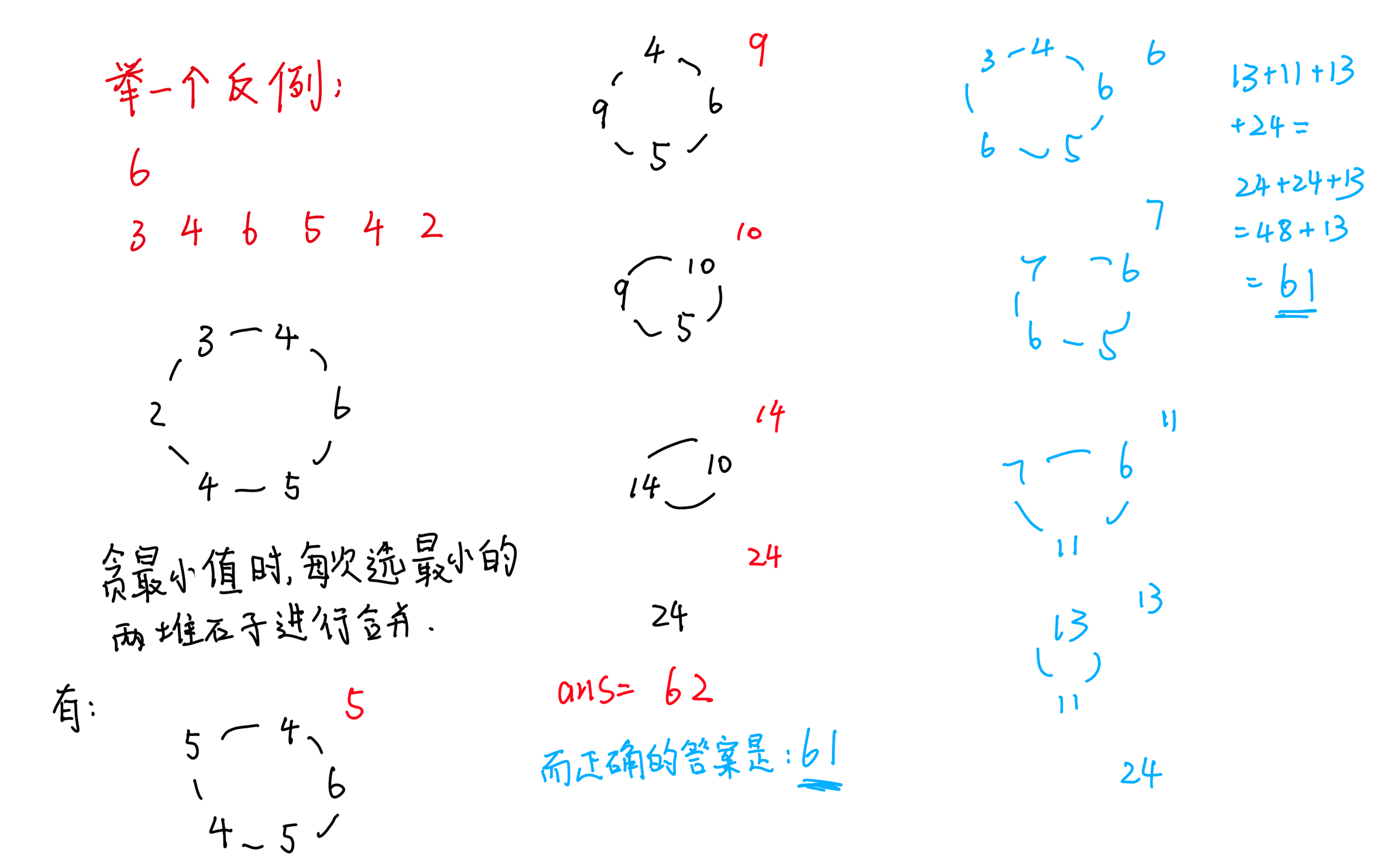
为什么不是贪心
区间dp的思路
首先是区间\(dp\)最基本的思路:f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+val)
区间\(dp\),顾名思义,就是求解某一个区间的(最值?)问题,而这一个区间是由两段合并而来的,这两段可以任意划分。
由转移式,我们很容易发现我们需要先求出区间长度较小的\(dp\)值,然后一步一步将区间的长度变大,最后得到我们需要的区间答案。于是,我们就有了以下代码:
//先要处理环
for(int i=2;i<=n;i++){//枚举每一种长度,每次只会算这一种长度的串的最值
for(int j=1;j<=n-i+1;j++){//枚举开始位置
for(int k=j;k<=j+i-2;k++){//枚举断开的位置
f[j][j+i-1]=max(f[j][j+i-1],f[j][k]+f[k+1][j+i-1]+sum[j+i-1]-sum[j-1]);
}
}
}
第一层循环从小到大枚举区间的长度,第二层循环枚举这个区间开始的位置,然后第三层循环枚举\(k\),即这个区间可能组成的方式(枚举划分点)。
对于这一道题而言,因为我们事先将环展开成为了链,而这个链的长度应该为\(2\times n-1\),然而实际上我们取\(2\times n\)也没有什么问题,只是会和第一种情况重复。又因为我们最后要求的区间长度只是为\(n\),所以代码实际上长这样:
for(int i=2;i<=n;i++){
for(int j=1;j<=2*n-i+1;j++){//这里改了一下
for(int k=j;k<=j+i-2;k++){
f[j][j+i-1]=max(f[j][j+i-1],f[j][k]+f[k+1][j+i-1]+sum[j+i-1]-sum[j-1]);
}
}
}
以上是针对于求石子合并所产生的最大值。其实求解最小值的思路也差不多,只是我们需要先将长度为二及以上的区间赋值为一个比较大的数(比如说\(inf\))。然后就可以得到以下代码:
for(int i=1;i<=2*n;i++){
for(int j=1;j<=2*n;j++){
if(i!=j) l[i][j]=inf;
}
}
for(int i=2;i<=n;i++){
for(int j=1;j<=2*n-i+1;j++){
for(int k=j;k<=j+i-2;k++){
f[j][j+i-1]=max(f[j][j+i-1],f[j][k]+f[k+1][j+i-1]+sum[j+i-1]-sum[j-1]);
l[j][j+i-1]=min(l[j][j+i-1],l[j][k]+l[k+1][j+i-1]+sum[j+i-1]-sum[j-1]);
}
}
}
以上就是这一道题的核心代码(没有优化)太弱啦
最后的代码
#include<bits/stdc++.h>
// #pragma GCC optimize(2)
const int inf=0x7fffffff;
using namespace std;
int read(){
int x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return ;
}
int n,a[300],sum[300],f[300][300],l[300][300];
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
a[n+i]=a[i];
}
for(int i=1;i<=2*n;i++){
sum[i]=sum[i-1]+a[i];
}
for(int i=1;i<=2*n;i++){
for(int j=1;j<=2*n;j++){
if(i!=j) l[i][j]=inf;
}
}
//先要处理环
for(int i=2;i<=n;i++){//枚举每一种长度,每次只会算这一种长度的串的最值
for(int j=1;j<=2*n-i+1;j++){//枚举开始位置
for(int k=j;k<=j+i-2;k++){//枚举断开的位置
f[j][j+i-1]=max(f[j][j+i-1],f[j][k]+f[k+1][j+i-1]+sum[j+i-1]-sum[j-1]);
l[j][j+i-1]=min(l[j][j+i-1],l[j][k]+l[k+1][j+i-1]+sum[j+i-1]-sum[j-1]);
}
}
}
int ansm=-inf;
int ansl=inf;
for(int i=1;i<=n;i++){
ansm=max(ansm,f[i][i+n-1]);
ansl=min(ansl,l[i][i+n-1]);
}
cout<<ansl<<endl<<ansm<<endl;
return 0;
}