通信题还没做。
JOISC19 D1T1 試験 (Examination)
双 log 很简单。但是单 log 才是这题的本质。
我们进行一些补集转换。我们能算的是什么?我们能算一条边在边界上的直角边平行于坐标轴的直角三角形数点,我们能算长方形数点。
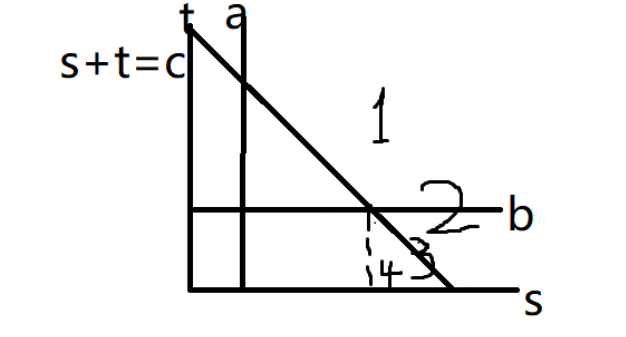
我们要算 1 的点数,那相当于 2 的点数减去 3 的点数再加上 4 的点数。这三个都是可以直接扫描线算的。
https://qoj.ac/submission/80220
JOISC2019 D1T2 聚会 Meetings
想出的做法比较垃圾。考虑维护目前点组成的虚树,然后重剖。钦定根为 1,我们找到 \(1\) 的重儿子 \(1\to r\),问 \((1,r,x)\),设结果为 \(w\)。如果问到的结果不在虚树内,那么就把 \(w\) 加入,然后 \(x\) 挂在 \(w\) 上(加入时在链上二分);如果结果为 \(x\),那么就代表在链上,直接二分;如果结果为链上的 \(y\),那么就递归在 \(y\) 子树问;如果为 \(r\) 就直接挂在 \(r\) 上;否则继续处理次重儿子。就这样做下去。复杂度感觉很奇怪,但是常数是很小的,所以也过去了。
JOISC19 D1T3 ナン (Naan)
日常不会做 ad-hoc。
我们把每个人的 \(n\) 等分点给全部求出来,设为 \(x_0=0,x_1,\dots,x_{n-1},x_n=l\)。那么对于第 \(i\) 段,我们找到 \(x_i\) 最小的剩余的那个人,把 \(x_i\) 作为第 \(i\) 个划分点 \(y_i\)。由于 \(y_{i-1}\) 一定 \(\le x_{i-1}\),所以这一段是满足要求的。
嗯,结束了!
https://qoj.ac/submission/80398
JOISC19 ふたつのアンテナ (Two Antennas)
考虑扫描线。我们不妨只算 \(h_j<h_i\) 的贡献,然后再反过来做一次就可以了。我们首先考虑以 \(i\) 作为时间,维护每个 \(j\) 在这个时刻是否存在。\(j\) 在 \(j+l_i\) 时插入,\(j+r_i\) 时删除,那么 \(i\) 的贡献就是 \(h_i\) 减去 \([i-r_i,i-l_i]\) 区间的 \(\min h_j\)。然后我们考虑如何处理区间问询。我们一样,每个线段树节点维护区间历史最大答案,而我们一个 \(i\) 相当于更新 \([i-r_i,i-l_i]\) 的答案。每个区间维护一个 tag,表示目前最大的覆盖这个区间的 \(h_i\),然后我们每次下放 tag 的时候就用这个 tag 去更新区间的历史最大答案(注意下方完了 tag 要直接删掉,不然可能会和后来插入的 \(j\) 一起更新答案,这是非法的)。
https://qoj.ac/submission/82201
JOISC19 ふたつの料理 (Two Dishes)
好题!
考虑一个暴力 DP:\(f(i,j)\) 表示前 \(i\) 个 \(A\),前 \(j\) 个 \(B\),最大价值。将 \(a,b\) 前缀和。令 \(A_i=S_i-a_i\),\(B_j\) 同理,那么式子化成 \(f(i,j)=\max \{f(i-1,j)+[b_j\le A_i],f(i,j-1)+[a_i\le B_j]\}\)。我们考虑记录 \(p_i=\max_j s.t. b_j\le A_i\),\(q_i\) 同理。钦定 \(j +\) 为右,\(i+\) 为下,即我们考虑向右走一步时,只有在 \((i,p_i)\) 之下时才会有贡献;考虑向下走一步时,只有在 \((q_j,j)\) 之上时才会右贡献。我们把所有 \(p\) 的贡献先加上然后取反,这样就能变成只有在点上面才能有贡献了。我们相当于就是要最大化路径覆盖的点之和。即假设我们的路径可以用一些 \((i,s_i)\) 表示,那么 \((x_u,y_u)\) (\((x_u,y_u)=(i-1,p_i+1)\) 或 \((q_i,i)\))产生贡献当且仅当 \(s_{x_u}\ge y_u\)。也就是说我们 \(i +1\) 的时候,会加上目前的点的左侧的贡献,即设 \(t_{i,j}\) 表示 \((i,[1,j])\) 的点的贡献和,那么稍微修改一下 \(f\) 的定义,使 \(f\) 不记录当前行的点的贡献,于是 \(f_{i,j}=\max \{f_{i,j-1},f_{i-1,j}+t_{i-1,j}\}\)。我们把 \(f_{i,j-1}\) 展开来,可以得到 \(f_{i,j}=\max_{k\le j} \{f_{i-1,k}+t_{i-1,k}\}\),相当于每一个 \((i-1,*)\) 的贡献点都会让一个后缀加,然后我们最后再给 \(f_i\) 做一次前缀 max 操作。我们考虑 \(f\) 的差分数组 \(g\),那么 \((i-1,j)\) 的贡献点的贡献为使 \(g_j\) 加上一个值,做前缀 max 操作相当于从右往左扫,然后遇到负数就和后面的正数去干成零。于是我们需要维护一个支持单点修改和区间赋 \(0\) 的线段树。
要注意线段树二分不能写假。
https://qoj.ac/submission/82471
JOISC19 指定都市 (Designated Cities)
考虑一个做法:钦定一个根,然后我们根必选,其它就是相当于一个选 \(k\) 条链使得其覆盖长度最大的问题了。
然后有一个很重要的观察!我们选 \(k\) 个点的方案,对于 \(k>2\),都是会继承上 \(k-1\) 的方案的!
这道题做不出来的问题在于这个东西,它在 \(k=1\) 的时候是特例,但对于 \(k>2\) 就是完全是对的。有一个很好的启发:当我们需要观察一些结论的时候,试图深入一些!
https://qoj.ac/submission/82592
JOISC19 ランプ (Lamps)
智障了好久。首先一些结论:\(\text{xor}\) 一定会垫在覆盖之后。于是我们需要去想到一个 DP:\(f(i,S)\) 表示目前考虑到 \([1,i]\), \(i\) 被操作覆盖的形态是 \(S\),然后就可以直接 DP 了。
https://qoj.ac/submission/82619
JOISC19 時をかけるビ太郎 (Bitaro, who Leaps through Time)
感觉比较 Educational 的题。
首先全部变换成 \([l_i-i-1,r_i-i-1]\)。然后相当于就是对于一个初始的 $a $,然后我们不断做 \(a=\max (a,l)\),\(a=\min(a,r)\),其中后者对答案会产生贡献。
考虑做一个信息的合并。对于两个相交的区间,我们发现它和这两个区间的交是等价的。而对于两个不交的区间 \(P_1,P_2\),我们依次走过 \(P_1,P_2\),我们发现无论我们从哪里开始走,经过这两个区间后得到的 \(x'\) 都和初始的 \(x\) 无关。而我们从初始往右走,在走到第一次区间无交集前,\(a\) 的贡献一定可以用一个 \(\max(0,a-x)\) 表示;走到第一次区间无交集之后,贡献就固定下来了。所以我们考虑记录在第一次遇到无交集前的 \(x\) 以及最后会从哪里出去 \(y\)。
我们考虑如何去描述这样的信息。我们可以敏锐地观察到,这样的信息是满足结合率的!所以对于链上的一个区间 \([x,y]\),区间 \([l_x,r_x],[l_{x+1},r_{x+1}],\dots,[l_{y,r_y}]\) 合并出来的结果只有两种:
- 这些区间存在一个交集。于是我们记录这些区间的交集,记其为 \((A,x,y)\)。
- 这些区间不存在交集。于是我们记录第一次无交集前的 \(x=\min(r)\),以及最后会从哪来出去 \(y\),以及第一次无交集之后的贡献 \(z\),记其为 \((B,x,y,z)\)。
我们定义一个函数 \(f(a,S)\),其中 \(S\) 为 \(A\) 或 \(B\) 类型,返回对于初始的 \(a\),经过 \(S\) 之后的位置。同理 \(g(a,S)\) 表示贡献。
现在考虑这些信息的合并:
- \(A_l+A_r\)
- \(x_r\le y_l\) 时,结果为区间的交;
- \(y_l\le x_r\) 时,结果为 \((B,y_l,x_r,0)\);
- \(y_r\le x_l\) 时,结果为 \((B,x_l,y_r,x_l-y_r)\)。
- \(B_l+B_r=(B,x_l,y_r,g(y_l,B_r)+z_l)\)。
- \(B_l+A_r=(B,x_l,f(y_l,A_r),g(y_l,A_r)+z_l)\)。
- \(A_l+B_r\)
- \(y _l\le x_r\) 时,结果为 \((B,y_l,y_r,z_r)\)。
- \(x_r\le x_l\) 时,结果为 \((B,x_l,y_r,x_l-x_r+z_r)\)。
- 否则,结果为 \(B_r\)。
https://qoj.ac/submission/83287
JOISC19 合併 (Mergers)
首先每个州会覆盖其形成的一棵虚树。合并两个虚树多覆盖的边相当于两个虚树的根的路径。我们处理出哪些边没有被覆盖,然后我们相当于就是要用尽量少的路径覆盖这些边。我们可以直接处理出这些边形成的虚树的叶节点数就行了。
https://qoj.ac/submission/83518
JOISC19 ケーキの貼り合わせ (Cake 3)
我们对所有蛋糕按 \(c\) 从小到大排序,那么我们就是需要选择一个区间 \([l,r]\),使得区间中最大的 \(m\) 个值加上 \(2c_r-2c_l\) 最大。这个关于 \(m\) 的凸性是没有的,但是每个右端点的最优的左端点一定是单调增的,于是整体二分分治即可。
https://qoj.ac/submission/83542
JOISC2019 Day4 Minerals 矿物
首先考虑一种分治方法:我们花 \(n\) 次问询把它分成左部和右部。然后每次我们取一半的左部,问一下右部,然后把那些能和这一半的左部匹配起来的递归下去,把不能匹配的和另一半左部递归下去。这个'取'的操作,可能是加入一些左部点,也可能是删去一些左部点,取决于进入递归时的情况。
这样做问询次数是 \(n+1.5n\log n\) 的。过不了。
然后加入这两个大优化,优化完了就能很轻松地过去了!
- 我们观察到我们每次操作左部的次数是 \(pn\)(\(0<p<1\)),那么我们的问询次数 \(T(n)=T(pn)+T((1-p)n)+(1+p)n\)。这个并不是在 \(p=0.5\) 时取到最值。应该是大概取 \(0.36\) 附近的一个数取到最值。可以求导求精确值。
- 我们每次实际上并不需要问完所有的 \(b\)。一旦和左部匹配的取满了,或者和左部配不上的取满了,那么剩下的都不用问了。