博弈论学习笔记-526互联

引入

OI 中的博弈论主要研究的是公平组合游戏。

什么是公平组合游戏（\(\text{Impartial Game}\)）？

游戏有两个人参与，双方轮流作出决策，双方均知道完整的游戏信息。
任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关。
游戏中同一个状态不能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。

也就是说，公平组合游戏不存在平局状态，对于游戏中某一状态，一定存在先手必胜或是先手必败。

一个前提

两个人都是绝对聪明的，不用考虑某位玩家随机走的情况。

基本模型

巴什博弈

有一堆石子，共 \(n\) 个，两个人轮流从这堆物品中取走至少 \(1\) 个，至多 \(m\) 个石子，第一个无法行动的玩家失败。

若 \((m + 1)\ | \ n\)，则先手必败，否则先手必胜。

证明：

若 \(n \leq m\)，先手可以一次取完所有，先手必胜。
若 \(n=m+1\)，因为一次最多只能选 \(m\) 个，所以无论先手拿走几个，后手都能拿走剩下的部分，即先手必败。
若 \(n = (m+1)r\)，先手拿走 \(k(1\leq k \leq m)\) 个，那么后者再拿走 \(m+1-k\) 个，就剩下 \((m+1)(r-1)\) 个，每次减少 \(m+1\)，后手按照这样的策略继续进行，后手必胜。
若 \(n = (m+1)r+s\)，其中 \(r\) 为任意自然数且 \(s \leq m\)，那么先手先拿走 \(s\) 个，就变成了第 \(3\) 条的状态，但对于新状态，此时的先手是原本游戏的后手。新状态中先手必败，所以原本游戏中先手必胜。

~~（感觉巴什博弈经常会作为酒桌游戏出现）~~

威佐夫博弈

有两堆石子，两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，第一个无法行动的玩家失败。

定义奇异局势：先手必败的局面。

两个人如果都采用正确操作，那么面对非奇异局势，先手必胜；反之，则后手必胜。

给出一个局势 \((a,b)\)，如何判断该局势是否为奇异局势。

利用公式：\(a= \left\lfloor \frac{\sqrt{5}+1}{2}(b-a) \right\rfloor\) 时，该局势为奇异局势。

~~证明不会。~~

Nim 博弈

有 \(n\) 堆石子，每堆有 \(a_i\) 个，两个玩家轮流取走任意一堆的任意个物品，但不能不取，第一个无法行动的玩家失败。

局面为先手必败，当且仅当各堆石子数量异或和为 \(0\)。

下面以 \(\text{Nim}\) 博弈来详细解释公平组合游戏。

博弈图和状态

如果将每个状态视为一个节点，再从每个状态向它的后继状态连边，我们就可以得到一个博弈状态图。

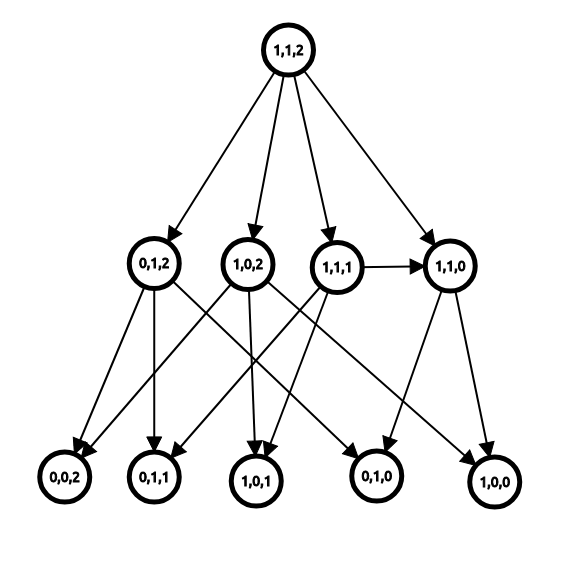
一个状态的儿子就是它的后继状态。

定义： 必胜状态 为 先手必胜的状态，必败状态 为 先手必败的状态。

但要注意我们下面所说的先手，指的是从当前状态开始向其后继状态转移的先手，而非整场游戏的先手。

通过推理，我们可以得到如下三条定理：

定理 1：没有后继状态的状态是必败状态。

如果无法向下一个状态转移，所以先手无法行动，该状态是必败状态。

定理 2：一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。

如果该状态有一个后继状态是必败状态，那么先手可以通过转移到该后继状态使得当前状态的后手必败，所以当前状态是必胜状态。

定理 3：一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。

如果当前状态的后继状态存在必败状态，先手就可以转移到该必败状态，那么当前状态的先手就得以胜利，所以该状态不是必败状态。

所以，如果一个状态的后继状态中存在必败状态，那么该状态不可能是必败状态。

Nim 和

我们可以通过画博弈图判断该局面是否先手必胜，但是时间复杂度太高。

我们定义 \(\text{Nim}\) 和为 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n\)。

当且仅当 \(\text{Nim}\) 和为 \(0\) 时，该局面为必败状态，否则该状态为必胜状态。

证明

以下给出的三个定理即为上面三个定理的形式化。

定理 1：没有后继状态的状态是必败状态。

如果一个状态没有后继状态，那么这个状态只能是全为 \(0\) 的局面（即所有石子都被拿走），此时 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n=0\)，符合该局面为必败状态。

定理 2：对于 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n \neq 0\) 的局面，一定存在某种移动使得 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n = 0\)。

我们假设 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n=k,k \neq 0\)，存在后继状态使得 \(a_i\) 改为 \(a_i'\)，则 \(a_i'=a_i \oplus k\)。

假设 \(k\) 的二进制最高位位 \(d\)，那么有 \(2^d \leq k < 2^{d+1}\)。由于最终异或和为 \(0\)，又根据异或的归零律，所以一定存在奇数个 \(a_i\) 的二进制第 \(d\) 位为 \(1\)。那么满足这个条件的 \(a_i\) 由于二进制下第 \(d\) 位为 \(1\)，而 \(a_i \oplus k\) 二进制下第 \(d\) 位为 \(0\) 且第 \(d\) 位为最高位，所以 \(a_i > a_i \oplus k\)，这个移动合法。

定理 3：对于 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n=0\) 的局面，一定不存在某种移动使得\(a_1 \oplus a_2 \oplus \cdots \oplus a_n=0\)。

假设我们把 \(a_i\) 转移为 \(a_i'\)，因为 \(a_i \oplus a_i'=0\)，所以 \(a_i = a_i'\)，显然，这种移动是非法的，该定理正确。

SG 函数和 SG 定理

给出一个定义：
\(\operatorname{mex}\) 函数的值为不属于集合 \(S\) 的最小非负整数，即：

\[\operatorname{mex}(S)=min \left\{ x \right\}(x \notin S,x \in N) \]

对于状态 \(x\) 和它的所有 \(k\) 个后继状态 \(y_1,y_2,\dots,y_k\)，定义 \(\text{SG}\) 函数：

\[\operatorname{SG}(x)=\operatorname{mex}\left\{\operatorname{SG}(y_1),\operatorname{SG}(y_2),\dots,\operatorname{SG}(y_k)\right\} \]

对于由 \(n\) 个有向图游戏组成的组合游戏，设他们的起点分别是 \(s_1,s_2,\dots,s_n\)，有定理：

当且仅当 \(\operatorname{SG}(s_1) \oplus \operatorname{SG}(s_2) \oplus \ldots \oplus \operatorname{SG}(s_n) \neq 0\) 时，这个游戏先手必胜。同
时，这是这一个组合游戏的游戏状态 \(x\) 的 SG 值。

这个就是我们 SG 定理，它适用于 任何公平的两人游戏（好强）。

我们用 Nim 游戏举个栗子，来解释一下 SG 函数。

总共有 \(n\) 堆石子，可以看作 \(n\) 个有向图游戏，每个游戏的起点分别是 \(a_1,a_2,\dots,a_n\)。

假设一次最多只能拿 \(m\) 个石子，那么对于状态 \(x\)，它可以从 \(\left\{ x-1,x-2,\dots,x-m \right\}\) 转移过来，那么

\[\operatorname{SG}(x)=\operatorname{mex}\left\{\operatorname{SG}(x-1),\operatorname{SG}(x-2),\dots,\operatorname{SG}(x-m)\right\} \]

这里小括号里的 \(x,x-1\) 都是指游戏状态，而不是一个确定的值。

具体栗子，例如一次最多能拿 \(2\) 个石子。

容易得到，\(\operatorname{SG}(0)=0\)，\(\operatorname{SG}(1)=1\)，\(\operatorname{SG}(2)=2\)。

那么对于 \(x=3\)，有 \(\operatorname{SG}(3)=\operatorname{mex}\left\{\operatorname{SG}(2),\operatorname{SG}(1)\right\}=0\)。

依次类推，我们可以得知 \(\operatorname{SG}(a_i)\) ，并根据 SG 定理判断输赢情况。

还有一句要提，Nim 游戏实际上可以分为 \(n\) 个巴什博弈作为子游戏，所以 Nim 游戏的求解也可以理解为运用 SG 定理求解 \(n\) 个巴什博弈的组合游戏。

证明

有一个十分严谨的证明。

不过我们来口胡一下。

假设我们有一个 SG 值为 \(k\) 的状态，那么它必然能转移到 SG 值为 \(j(0 < j < k)\) 的状态，其实就相当于一个有 \(k\) 个石子的堆被拿走了 \(k-j\) 个。

这样我们就把 SG 值转化成了石子数量，把 SG 定理的证明转化成了 Nim 和的证明。

有向图游戏

给定一个有向无环图，图中有唯一的起点，在起点上放有一枚棋子。两名玩家交替把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。

绝大多数公平组合游戏都能转化为有向图游戏：每个局面相当于图中的一个结点，合法行动是图的有向边。

将 Nim 游戏转换为有向图游戏

我们可以将一个有 \(x\) 个石子的堆看成一个结点 \(x\)，当且仅当 \(y < x\) 时，存在从 \(x\) 到 \(y\) 的有向边。

那么由 \(n\) 个堆组成的 Nim 游戏，可以视为 \(n\) 个有向图游戏。

可以得到，\(\operatorname{SG}(x)=x\)，再根据 SG 定理可以得出 Nim 和的结论。

~~回头有空补一些博弈论的题~~

参考资料

\[\text{END} \]