Prototypical contrastive learning of unsupervised representations

abstract

这篇论文介绍了原型对比学习（PCL），一种将对比学习与聚类相结合的无监督表示学习方法。PCL不仅为实例区分任务学习低层特征，更重要的是将聚类发现的语义结构编码到所学嵌入空间中。具体而言，我们引入原型作为潜在变量，以帮助在EM（Expectation-Maximization）框架中找到网络参数的最大似然估计。我们通过迭代执行E步骤，即通过聚类找到原型分布；执行M步骤，即通过对比学习优化网络。我们提出了ProtoNCE损失，这是对比学习的InfoNCE损失的广义版本，鼓励表征更接近其分配的原型。在多个基准测试中，PCL在低资源迁移学习方面表现优于最先进的基于实例的对比学习，并实现了显著的改进。

Introduction

从本质上讲，基于实例的对比学习导致了一个嵌入空间，其中所有实例都很好地分离，并且每个实例在局部是光滑的（即带有扰动的输入具有相似的表示）。

尽管它们在性能上有所提高，但实例区分方法存在一个共同的弱点：不鼓励表征对数据的语义结构进行编码。这个问题的根源在于逐实例对比学习，只要两个样本来自不同实例，就将它们视为负样本对，而不考虑它们的语义相似性。由于生成了数千个负样本来形成对比损失，这一事实被放大了，导致许多具有相似语义的负对，在嵌入空间中被推开。

本文提出了一种新的无监督表示学习框架——原型对比学习(PCL)，它将数据的语义结构隐式编码到嵌入空间中。图1显示了PCL的示意图。原型被定义为“一组语义相似实例的代表性嵌入”。我们为每个实例分配了几个不同粒度的原型，并构建了一个对比损失，该损失使样本的嵌入比其他原型更接近其相应的原型。在实践中，我们可以通过对嵌入执行聚类来找到原型。

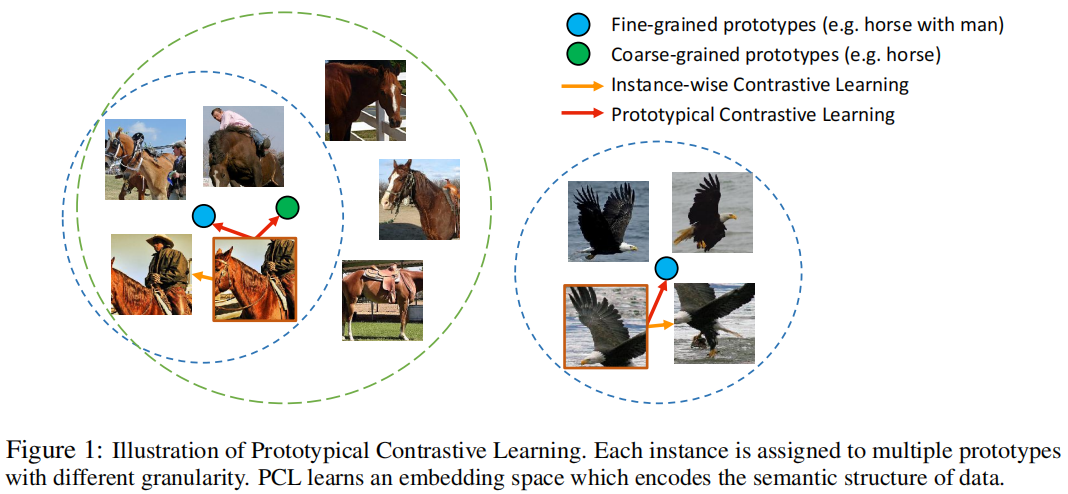
我们将原型对比学习制定为期望最大化(EM)算法，其目标是通过迭代逼近和最大化对数似然函数来找到最能描述数据分布的深度神经网络(DNN)的参数。具体来说，我们将原型作为附加的潜在变量引入，并通过执行k-means聚类来估计它们在E步中的概率。在m步中，我们通过最小化我们提出的对比损失(即ProtoNCE)来更新网络参数。在假设每个原型周围的数据分布是各向同性高斯分布的情况下，最小化ProtoNCE相当于最大化估计的对数似然。在EM框架下，广泛使用的实例识别任务可以解释为原型对比学习的一个特例，其中每个实例的原型是其增强特征，并且每个原型周围的高斯分布具有相同的固定方差。

本文的贡献可以概括为以下几点:

我们提出了原型对比学习，这是一种连接对比学习和聚类的无监督表征学习的新框架。鼓励学习的表征来捕获数据集的分层语义结构。
我们给出了一个理论框架，将PCL表述为基于期望最大化(EM)的算法。聚类和表示学习的迭代步骤可以解释为逼近和最大化对数似然函数。基于实例辨别的方法在本文提出的EM框架中属于特例。
我们提出了一种新的对比损失算法ProtoNCE，它通过动态估计每个原型周围特征分布的集中程度来改进广泛使用的InfoNCE。ProtoNCE还包括一个InfoNCE术语，在这个术语中，实例嵌入可以被解释为基于实例的原型。我们从信息论的角度解释了PCL，通过展示学习的原型包含了更多关于图像类的信息。
PCL在多个基准上优于实例对比学习，在低资源迁移学习方面有了实质性的改进。PCL也导致了更好的聚类结果。

Instance-wise contrastive learning

现有的基于实例对比学习的方法存在以下两大局限性

利用低层线索就可以区分不同的实例，学习的嵌入不一定能捕获高级语义。实例分类的准确性通常会在10个epoch内迅速上升到很高的水平(>90%)，而进一步的训练给出的信息信号有限，这一事实支持了这一点。最近的一项研究也表明，更好的实例区分性能可能会降低下游任务的性能
对足够多的负实例进行采样会不可避免地产生具有相似语义的负对。它们在嵌入空间中应该更接近，但被对比的损失分开了。在(Saunshi et al.， 2019)中，这一问题被定义为类碰撞，并被证明会损害表征学习。从本质上讲，实例识别学习一个嵌入空间，它只保留每个实例周围的局部平滑，但在很大程度上忽略了数据集的全局语义结构

PROTOTYPICAL CONTRASTIVE LEARNING

PRELIMINARIES

给定训练集 \(X=\{x_1,x_2,\dots,x_n\}\) ，无监督视觉表示学习旨在学习一个嵌入函数 \(f_\theta\) (通过DNN实现)，该函数将 \(X\) 映射到 \(V=\{v_1,v_2,\dots,v_n\}\)，其中 \(v_i = f_\theta(x_i)\)，使得 \(v_i\) 最能描述 \(x_i\)。基于实例的对比学习通过优化对比损失函数来实现这一目标，例如 InfoNCE (Oord等人，2018;He et al.， 2020)，定义为:

\[\mathcal{L}_{\text{InfoNCE}}=\sum_{i=1}^n-\log\frac{exp(v_i\cdot v_i^{'} / \tau)}{\sum_{j=0}^r exp(v_i \cdot v_j^{'} / \tau)} \tag{1} \]

其中 \(v_i\) 和 \(v_i^{'}\) 是实例 \(i\) 的正嵌入，并且 \(v_j^{'}\) 包括一个正嵌入和其他实例的 \(r\) 个负嵌入，并且 \(\tau\) 是温度超参数。在MoCo (He et al.， 2020)中，这些嵌入是通过将 \(x_i\) 输入到参数为 \(\theta^{'}\) 的动量编码器获得的，即 \(v_i^{'} = f_{\theta^{'}} (x_i)\)，其中 \(\theta^{'}\) 是 \(\theta\) 的移动平均值。

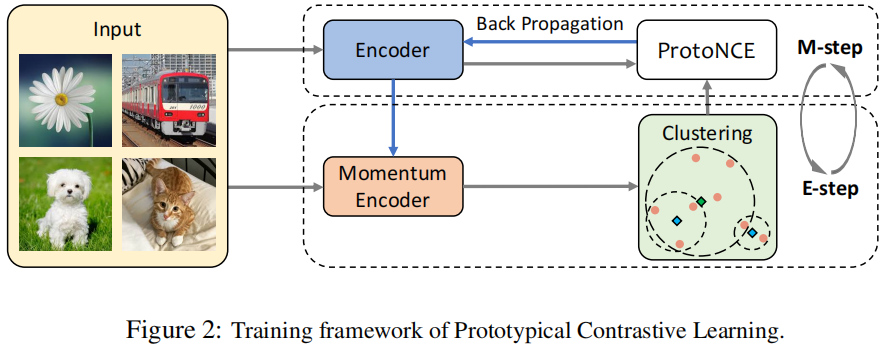
在原型对比学习中，我们使用原型 \(c\) 代替 \(v^{'}\) ，并用每个原型的聚集度估计 \(\phi\) 代替固定温度 \(\tau\)。我们的训练框架概述如图2所示，其中聚类和表示学习在每个epoch迭代地执行。

PCL AS EXPECTATION-MAXIMIZATION

我们的目标是找到最大化观察到的 \(n\) 个样本的对数似然函数的网络参数\(\theta\)：

\[\theta^*=\underset{\theta}{\arg \max } \sum_{i=1}^n \log p\left(x_i ; \theta\right) \tag{2} \]

我们假设观察到的数据 \(\left\{x_i\right\}_{i=1}^n\) 与表示数据的原型的潜在变量 \(C=\left\{c_i\right\}_{i=1}^k\) 相关联。通过这种方式，我们可以将对数似然函数重新写成：

\[\theta^*=\underset{\theta}{\arg \max } \sum_{i=1}^n \log p\left(x_i ; \theta\right)=\underset{\theta}{\arg \max } \sum_{i=1}^n \log \sum_{c_i \in C} p\left(x_i, c_i ; \theta\right) \tag{3} \]

直接优化这个函数很困难，因此我们使用一个替代函数来对它进行下界估计：

\[\sum_{i=1}^n \log \sum_{c_i \in C} p\left(x_i, c_i ; \theta\right)=\sum_{i=1}^n \log \sum_{c_i \in C} Q\left(c_i\right) \frac{p\left(x_i, c_i ; \theta\right)}{Q\left(c_i\right)} \geq \sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log \frac{p\left(x_i, c_i ; \theta\right)}{Q\left(c_i\right)}, \tag{4} \]

其中\(Q\left(c_i\right)\)表示对\(c\)的某种分布\(\left(\sum_{c_i \in C} Q\left(c_i\right)=1\right)\)，推导的最后一步使用了Jensen不等式。为了使等号成立，我们要求\(\frac{p\left(x_i, c_i ; \theta\right)}{Q\left(c_i\right)}\)是一个常数。因此，我们有：

\[Q\left(c_i\right)=\frac{p\left(x_i, c_i ; \theta\right)}{\sum_{c_i \in C} p\left(x_i, c_i ; \theta\right)}=\frac{p\left(x_i, c_i ; \theta\right)}{p\left(x_i ; \theta\right)}=p\left(c_i ; x_i, \theta\right) \tag{5} \]

忽略方程（4）中的常数项\(-\sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log Q\left(c_i\right)\)后，我们应该最大化：

\[\sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log p\left(x_i, c_i ; \theta\right) \tag{6} \]

E-step

在这一步中，我们的目标是估计\(p\left(c_i ; x_i, \theta\right)\)。为了实现这一目标，我们对由动量编码器给出的特征 \(v_i^{\prime}=f_{\theta^{\prime}}\left(x_i\right)\) 执行 \(k\)-means，以获得 \(k\) 个簇。我们将原型 \(c_i\) 定义为第 \(i\) 个簇的中心。然后，我们计算 \(p\left(c_i ; x_i, \theta\right)=\mathbb{1}\left(x_i \in c_i\right)\)，其中 \(\mathbb{1}\left(x_i \in c_i\right)=1\) 表示 \(x_i\) 属于由 \(c_i\) 表示的簇；否则 \(\mathbb{1}\left(x_i \in c_i\right)=0\)。类似于MoCo，我们发现从动量编码器获得的特征产生了更一致的簇。

M-step

基于E-step 的结果，我们已经准备好最大化方程（6）中的下界。

\[\begin{aligned} \sum_{i=1}^n \sum_{c_i \in C} Q\left(c_i\right) \log p\left(x_i, c_i ; \theta\right) & =\sum_{i=1}^n \sum_{c_i \in C} p\left(c_i ; x_i, \theta\right) \log p\left(x_i, c_i ; \theta\right) \\ & =\sum_{i=1}^n \sum_{c_i \in C} \mathbb{1}\left(x_i \in c_i\right) \log p\left(x_i, c_i ; \theta\right) \end{aligned} \tag{7} \]

在聚类质心均匀先验的假设下，有:

\[p(x_i,c_i;\theta)=p(x_i;c_i,\theta)p(c_i;\theta)=\frac{1}{k}\cdot p(x_i;c_i,\theta) \tag{8} \]

在这里，我们将每个\(c_i\)的先验概率\(p\left(c_i ; \theta\right)\)设置为\(1 / k\)，因为我们没有提供任何样本。
我们假设每个原型周围的分布是各向同性的高斯分布，这导致：

\[p\left(x_i ; c_i, \theta\right)=\exp \left(\frac{-\left(v_i-c_s\right)^2}{2 \sigma_s^2}\right) / \sum_{j=1}^k \exp \left(\frac{-\left(v_i-c_j\right)^2}{2 \sigma_j^2}\right), \tag{9} \]

其中\(v_i=f_\theta\left(x_i\right)\)，\(x_i \in c_s\)。如果我们对 \(v\) 和 \(c\) 都应用 \(\ell_2\) 归一化，则 \((v-c)^2=2-2 v \cdot c\)。将此与方程（3、4、6、7、8、9）结合起来，我们可以将最大对数似然估计写成：

\[\theta^*=\underset{\theta}{\arg \min } \sum_{i=1}^n-\log \frac{\exp \left(v_i \cdot c_s / \phi_s\right)}{\sum_{j=1}^k \exp \left(v_i \cdot c_j / \phi_j\right)}, \tag{10} \]

其中 \(\phi \propto \sigma^2\) 表示原型周围特征分布的集中程度，这将在稍后介绍。注意，方程（10）与方程（1）中的InfoNCE损失具有类似的形式。因此，InfoNCE可以解释为最大对数似然估计的一种特殊情况，其中特征 \(v_i\) 的原型是来自同一实例的增强特征 \(v_i^{\prime}\)（即\(c=v^{\prime}\)），并且每个实例周围特征分布的集中度是固定的（即\(\phi=\tau\)）。

在实际应用中，我们采用与 NCE 相同的方法，从中采样 \(r\) 个负原型来计算归一化项。我们还使用不同数量的簇\(K=\left\{k_m\right\}_{m=1}^M\)对样本进行\(M\)次聚类，这可以更稳健地估计编码层次结构的原型的概率。此外，我们添加了InfoNCE损失以保留局部平滑性的特性，并帮助引导聚类。我们的整体目标，即ProtoNCE，定义为：

\[\mathcal{L}_{\text {ProtoNCE }}=\sum_{i=1}^n-\left(\log \frac{\exp \left(v_i \cdot v_i^{\prime} / \tau\right)}{\sum_{j=0}^r \exp \left(v_i \cdot v_j^{\prime} / \tau\right)}+\frac{1}{M} \sum_{m=1}^M \log \frac{\exp \left(v_i \cdot c_s^m / \phi_s^m\right)}{\sum_{j=0}^r \exp \left(v_i \cdot c_j^m / \phi_j^m\right)}\right) . \tag{11} \]

CONCENTRATION ESTIMATION

每个原型周围的嵌入分布具有不同级别的集中度。我们使用 \(\phi\) 来表示集中度的估计，较小的 \(\phi\) 表示更高的集中度。在这里，我们使用与原型 \(c\) 在同一簇内的动量特征 \(\left\{v_z^{\prime}\right\}_{z=1}^Z\) 来计算\(\phi\)。理想情况下，如果（1）\(v_z^{\prime}\) 和 \(c\) 之间的平均距离小，并且（2）簇包含更多的特征点（即 \(Z\) 较大），则 \(\phi\) 应该很小（高集中度）。因此，我们将 \(\phi\) 定义为：

\[\phi=\frac{\sum_{z=1}^Z\left\|v_z^{\prime}-c\right\|_2}{Z \log (Z+\alpha)} \]

其中 \(\alpha\) 是一个平滑参数，以确保小簇不会有过大的 \(\phi\)。我们对每组原型 \(C^m\) 中的 \(\phi\) 进行归一化，使它们的平均值为 \(\tau\)。

在ProtoNCE loss（公式 (11)）中， \(\phi_s^m\) 作为嵌入 \(v_i\) 与其原型 \(c_s^m\) 之间相似度的比例因子。通过提出的\(\phi\)，松散簇中的相似性（较大的\(\phi\)）被缩小，使得嵌入与原型更加接近。相反，紧密簇中的嵌入（较小的\(\phi\)）相似性被放大，因此不太鼓励嵌入靠近原型。因此，使用 ProtoNCE 进行学习会产生具有类似集中度的更平衡的簇，如图3(a)所示。这防止了大多数嵌入崩溃到单一簇的平凡解，这是 DeepCluster（Caron等，2018年）中只能通过数据重新采样启发式地解决的问题。

Figure 3 (a)

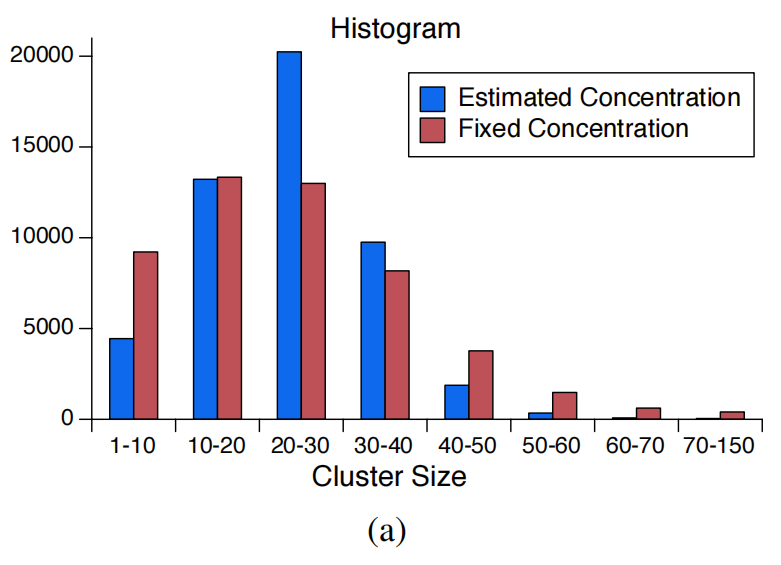
Figure 3 (a) 具有固定或估计聚集度的PCL (#clusters k=50000)的聚类大小直方图。为每个原型使用不同的 \(\phi\) 会产生具有相似大小的更平衡的簇，从而导致更好的表示学习。

MUTUAL INFORMATION ANALYSIS

已经证明，最小化InfoNCE等于最大化表征 \(V\) 和 \(V^{'}\) 之间互信息（MI）的下界(Oord et al., 2018).。类似地，最小化提出的ProtoNCE可以被视为同时最大化表征 \(V\) 和所有原型 \(\{V^{'},C^1,\cdots,c^M\}\) 之间的互信息。

这导致了更好的表示学习，原因如下：

编码器将学习原型之间的共享信息，并忽略存在于每个原型中的个体噪声。共享信息更有可能捕捉到更高层次的语义知识。
与实例特征相比，原型和类标签之间具有更大的互信息。

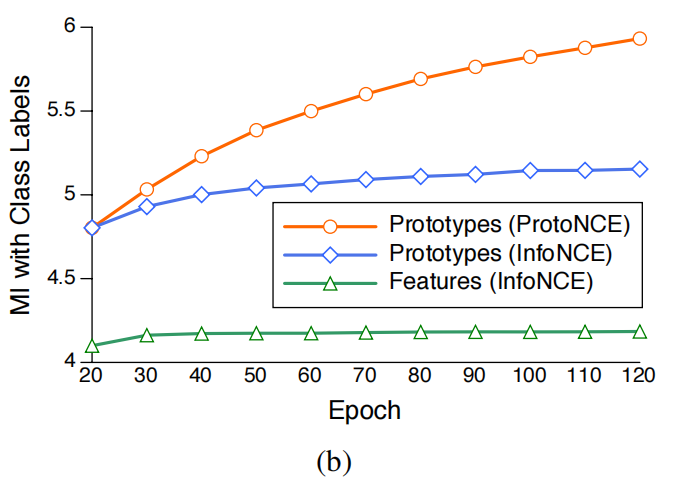
我们使用（Ross，2014）中的方法，估计了在ImageNet（Deng等，2009年）训练集中所有图像的实例特征（或它们对应的原型）与真实类标签之间的互信息。我们比较了我们方法（ProtoNCE）和MoCo（InfoNCE）的互信息。如图3(b)所示，与实例特征相比，由于聚类效应，原型与类标签具有更大的互信息。此外，与InfoNCE相比，使用ProtoNCE进行训练可以增加原型的互信息，表明随着训练的进行，学习到更好的表示以形成更有语义意义的簇。

PROTOTYPES AS LINEAR CLASSIFIER

对于PCL的另一种解释可以提供更多关于所学原型性质的见解。方程（10）中的优化类似于使用交叉熵损失来优化聚类分配概率 \(p(s; x_i , θ)\)，其中原型 \(c\) 代表线性分类器的权重。通过 k-means 聚类，线性分类器具有一组固定的权重，即每个簇中表征的均值向量\(c=\frac{1}{Z}\sum_{z=1}^Zv^{'}_z\)。

PSEUDO-CODE FOR PROTOTYPICAL CONTRASTIVE LEARNING

EXPERIMENIMPLEMENTATION DETAILSTS

IMPLEMENTATION DETAILS

需要注意一个细节：我们训练了200个epoch，其中我们在前20个epoch中只使用InfoNCE损失来预热网络。

IMAGE CLASSIFICATION WITH LIMITED TRAINING DATA

Low-shot classification

　实验在VOC07和Places205数据集上利用框架学到的表示使用 SVM 做图像分类实验。左 mAP、右ACC。表1显示了结果，其中我们的方法的性能大大优于MoCo和SimCLR

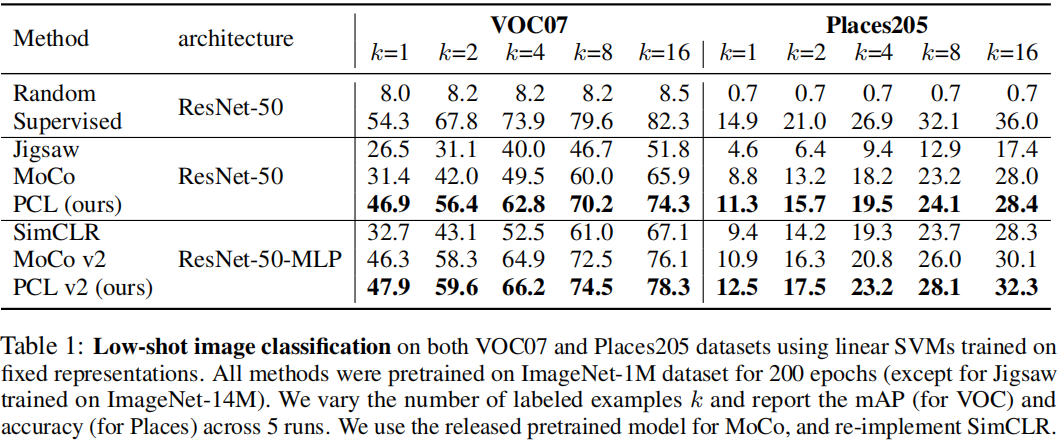
Semi-supervised image classification

评估学习到的表示是否可以为微调提供良好的基础。我们随机选择一个ImageNet训练数据(带标签)的子集(1%或10%)，并在这些子集上微调自监督训练模型。表2报告了在ImageNet验证集的top-5精度。

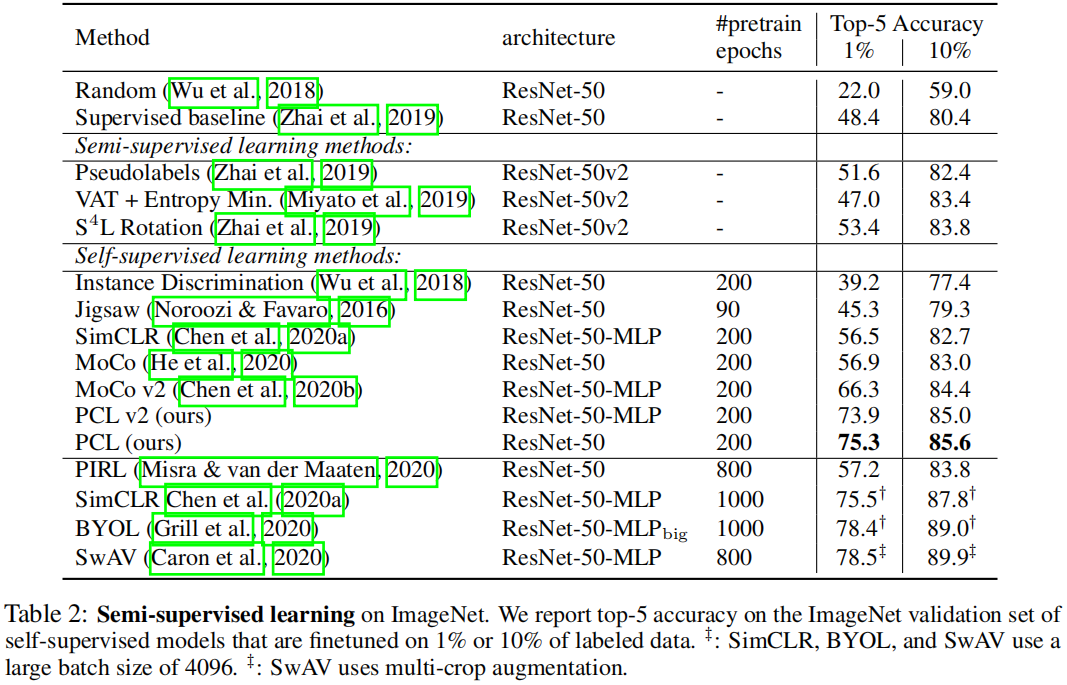
IMAGE CLASSIFICATION BENCHMARKS

Linear classifiers

我们使用整个带标签的训练数据，在固定的图像表示上训练线性分类器。

表3报告了结果。PCL在直接比较下优于MoCo，证明了所提出的原型对比损耗的优势。

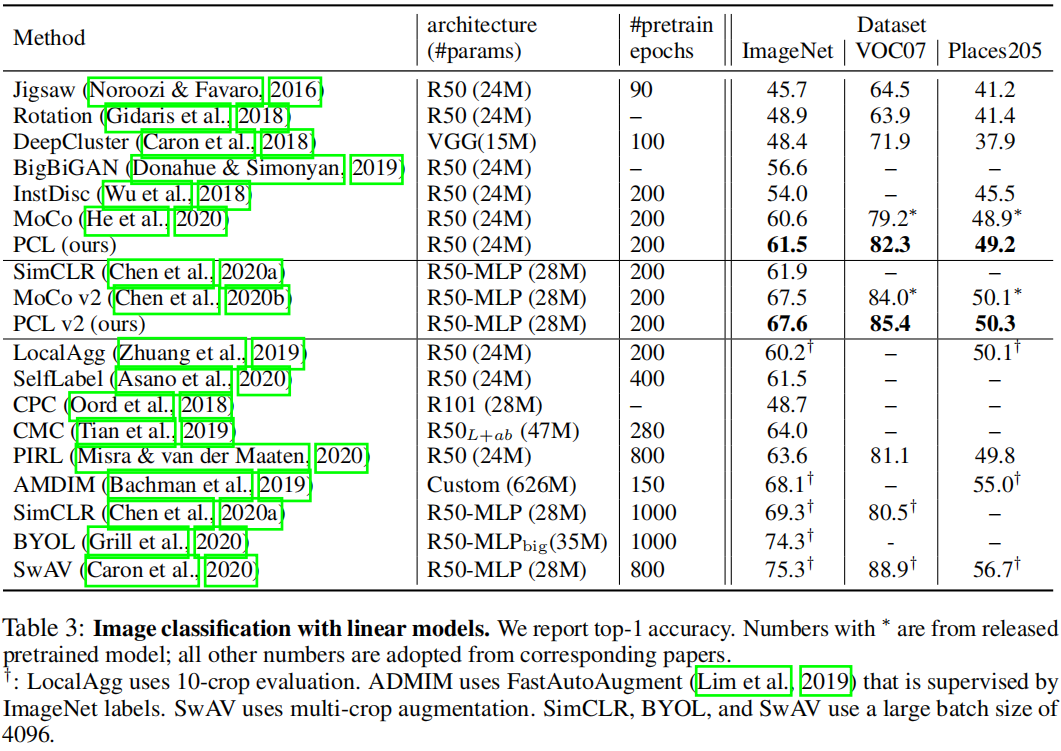
KNN classifiers

我们对ImageNet进行k近邻(kNN)分类。

对于具有特征 \(v\) 的查询图像，我们从动量特征中取其top-k个最近邻，并对其标签进行加权组合，其中权重由 \(\exp(v \cdot v^{'}_i/ \tau)\) 计算。表4报告了准确性。我们的方法大大优于以前的方法。

CLUSTERING EVALUATION

在表5中，我们使用不同方法学习的表示来评估ImageNet上的k-means聚类性能。PCL导致显著较高的调整互信息(AMI)得分。

OBJECT DETECTION

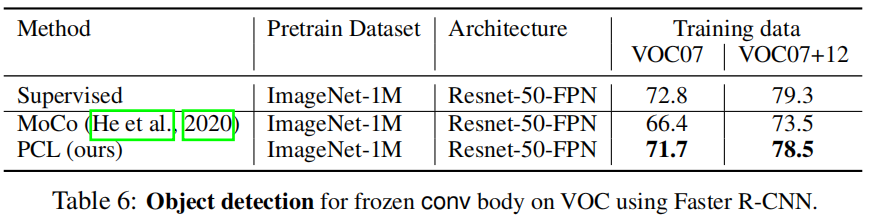
VISUALIZATION OF LEARNED REPRESENTATION

在图4中，我们使用t-SNE可视化ImageNet训练图像的无监督学习表示(Maaten & Hinton, 2008)。与MoCo学习到的表示相比，PCL学习到的表示形成了更多的分离簇，这也表明了其表示熵更低。

appendix

Jensen's inequality

参考琴生不等式

琴生不等式（英语：Jensen's inequality，台湾称作简森不等式[1]），或称延森不等式，以丹麦数学家约翰·延森命名。它给出积分的凸函数值和凸函数的积分值间的关系，在此不等式最简单形式中，阐明了对一平均做凸函数变换，会小于等于先做凸函数变换再平均。若将琴生不等式应用在二点上，就回到了凸函数的基本性质：过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方，即：

\[tf(x_1)+(1-t)f(x_2) \geq f(tx_1+(1-t)x_2),0 \leq t \leq 1 \]

Top-N

参考链接

Top-1 accuracy is the conventional accuracy: the model answer (the one with highest probability) must be exactly the expected answer.

Top-5 accuracy means that any of your model 5 highest probability answers must match the expected answer.

For instance, let's say you're applying machine learning to object recognition using a neural network. A picture of a cat is shown, and these are the outputs of your neural network:

Tiger: 0.4
Dog: 0.3
Cat: 0.1
Lynx: 0.09
Lion: 0.08
Bird: 0.02
Bear: 0.01

Using top-1 accuracy, you count this output as wrong, because it predicted a tiger.

Using top-5 accuracy, you count this output as correct, because cat is among the top-5 guesses.