线性回归的梯度下降
问题陈述:
让我们使用与之前相同的两个数据点 - 1000平方英尺的房子以300,000美元的价格出售,而2000平方英尺的房屋以500,000美元的价格出售。
import math, copy
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
from lab_utils_uni import plt_house_x, plt_contour_wgrad, plt_divergence, plt_gradients
# Load our data set
x_train = np.array([1.0, 2.0]) #features
y_train = np.array([300.0, 500.0]) #target value
成本函数:
#Function to calculate the cost
def compute_cost(x, y, w, b):
m = x.shape[0]
cost = 0
for i in range(m):
f_wb = w * x[i] + b
cost = cost + (f_wb - y[i])**2
total_cost = 1 / (2 * m) * cost
return total_cost
梯度下降摘要
线性模型,在线性回归中,您可以利用输入的训练数据来拟合参数?,?。通过最小化我们预测之间的误差??,?(?(?))以及实际数据?(?)。
该措施被称为????, ?(?,?)。公式:1
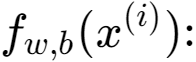
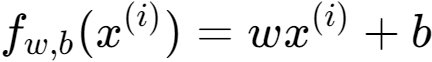
在训练数据中,您可以衡量我们所有培训样本的成本?(?),?(?),公式:2

梯度下降被描述为。公式:3
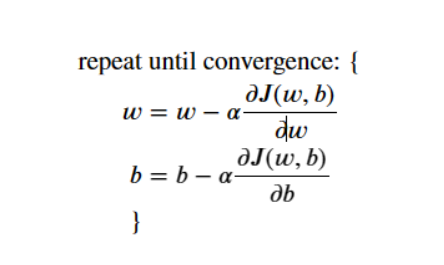
梯度定义为,更新任何参数之前计算所有参数的偏导数。公式:4、5
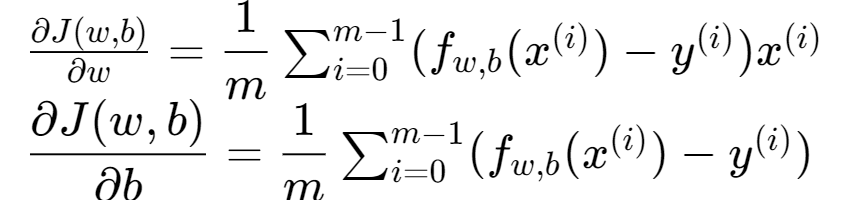
实现梯度下降:
- compute_gradient实现上述等式(4)和(5)
- compute_cost实现上面的公式 (2)(来自先前实验的代码)
- gradient_descent,利用compute_gradient和compute_cost- - - -
# compute_gradient
def compute_gradient(x, y, w, b):
"""
计算线性回归的梯度
x(ndarray(m,)):数据,m个示例
y(ndarray(m,)):目标值
w、 b(标量):模型参数
∂?(?,?)∂? = dj_db.
dj_dw(标量):参数w的成本w.r.t.的梯度
dj_db(标量):相对于参数b的成本梯度
"""
# Number of training examples
m = x.shape[0]
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x[i] + b
dj_dw_i = (f_wb - y[i]) * x[i]
dj_db_i = f_wb - y[i]
dj_db += dj_db_i
dj_dw += dj_dw_i
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
梯度下降如何利用成本相对于某一点参数的偏导数来更新该参数。使用函数compute_gradient来查找并绘制成本函数相对于其中一个参数的一些偏导数
plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()
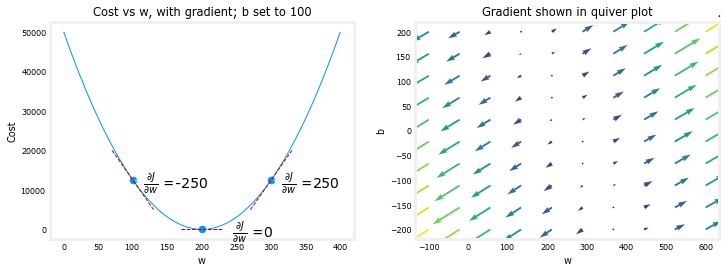
左图显示了?(?,?)∂?或成本曲线相对于?在三个点上。在图的右侧,导数是正的,而在左侧,导数是负的。由于“碗状”,导数将始终导致梯度下降到梯度为零的底部。左侧的绘图已固定?=100。梯度下降将同时利用?(?,?)∂? 和?(?,?)∂?以更新参数。
右边的“颤动图”提供了一种查看两个参数梯度的方法。箭头的大小反映了该点处梯度的大小。箭头的方向和斜率反映了?(?,?)∂?和?(?,?)∂?。在那一点上。请注意,梯度指向远离最小值的位置。复习上面的等式(3)。缩放后的梯度从的当前值中减去?或?。这将使参数朝着降低成本的方向移动。
梯度下降
现在可以计算梯度,上式(3)中描述的梯度下降可以在下面的中实现。注释中描述了实现的详细信息。下面,您将利用此功能找到gradient_descent ?和 ?在训练数据上。
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function):
"""
执行梯度下降以拟合w,b。通过获取更新w、b
带学习率alpha的num_iters梯度步长
Args:
x(ndarray(m,)):数据,m个示例
y(ndarray(m,)):目标值
w_in,b_in(标量):模型参数的初始值
alpha(浮动):学习率
num_iters(int):运行梯度下降的迭代次数
cost_function:调用以产生成本的函数
gradient_function:要调用以生成梯度的函数
Returns:
w(标量):运行梯度下降后参数的更新值
b(标量):运行梯度下降后参数的更新值
J_history(列表):成本值的历史记录
p_history(list):参数历史[w,b]
"""
w = copy.deepcopy(w_in) # #避免修改全局w_in
# 一个数组,用于存储每次迭代的成本J和w,主要用于以后绘图
J_history = []
p_history = []
b = b_in
w = w_in
for i in range(num_iters):
# 使用gradient_function计算梯度并更新参数
dj_dw, dj_db = gradient_function(x, y, w , b)
# 使用上面的公式(3)更新参数
b = b - alpha * dj_db
w = w - alpha * dj_dw
# 每次迭代节省成本J
if i<100000: #防止资源耗尽
J_history.append( cost_function(x, y, w , b))
p_history.append([w,b])
# #每隔10次打印一次成本,如果<10,则重复次数相同
if i% math.ceil(num_iters/10) == 0:
print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",
f"w: {w: 0.3e}, b:{b: 0.5e}")
return w, b, J_history, p_history #返回w和J,w历史以进行绘图
#初始化参数
w_init = 0
b_init = 0
#一些梯度下降设置
iterations = 10000
tmp_alpha = 1.0e-2
#运行梯度下降
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")
Iteration 0: Cost 7.93e+04 dj_dw: -6.500e+02, dj_db: -4.000e+02 w: 6.500e+00, b: 4.00000e+00
Iteration 1000: Cost 3.41e+00 dj_dw: -3.712e-01, dj_db: 6.007e-01 w: 1.949e+02, b: 1.08228e+02
Iteration 2000: Cost 7.93e-01 dj_dw: -1.789e-01, dj_db: 2.895e-01 w: 1.975e+02, b: 1.03966e+02
Iteration 3000: Cost 1.84e-01 dj_dw: -8.625e-02, dj_db: 1.396e-01 w: 1.988e+02, b: 1.01912e+02
Iteration 4000: Cost 4.28e-02 dj_dw: -4.158e-02, dj_db: 6.727e-02 w: 1.994e+02, b: 1.00922e+02
Iteration 5000: Cost 9.95e-03 dj_dw: -2.004e-02, dj_db: 3.243e-02 w: 1.997e+02, b: 1.00444e+02
Iteration 6000: Cost 2.31e-03 dj_dw: -9.660e-03, dj_db: 1.563e-02 w: 1.999e+02, b: 1.00214e+02
Iteration 7000: Cost 5.37e-04 dj_dw: -4.657e-03, dj_db: 7.535e-03 w: 1.999e+02, b: 1.00103e+02
Iteration 8000: Cost 1.25e-04 dj_dw: -2.245e-03, dj_db: 3.632e-03 w: 2.000e+02, b: 1.00050e+02
Iteration 9000: Cost 2.90e-05 dj_dw: -1.082e-03, dj_db: 1.751e-03 w: 2.000e+02, b: 1.00024e+02
(w,b) found by gradient descent: (199.9929,100.0116)
本从很大开始,然后迅速下降。
偏导数也变小,先快,后慢。当过程接近“碗底”时,由于该点导数的值较小,因此进度较慢。dj_dw dj_db。
尽管学习率 alpha 保持不变,但进度放缓。
梯度下降的成本与迭代
成本与迭代图是梯度下降进度的有用度量。
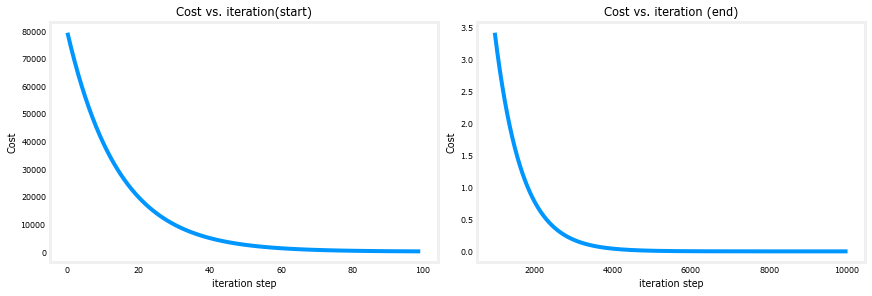
成功运行后,成本应始终降低。最初成本的变化如此之快,因此在与最终下降不同的比例上绘制初始体面是很有用的。
在下面的图中,请注意轴和迭代步骤上的成本比例。
# 绘图成本与迭代
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)"); ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost') ; ax2.set_ylabel('Cost')
ax1.set_xlabel('iteration step') ; ax2.set_xlabel('iteration step')
plt.show()
预测:
现在您已经发现了参数的最佳值 ? 和 ?,
现在可以使用该模型根据我们学习的参数预测住房价值。
预测值几乎与相同住房的训练值相同。此外,不在预测中的值与期望值一致。
print(f"1000 sqft house prediction {w_final*1.0 + b_final:0.1f} Thousand dollars")
print(f"1200 sqft house prediction {w_final*1.2 + b_final:0.1f} Thousand dollars")
print(f"2000 sqft house prediction {w_final*2.0 + b_final:0.1f} Thousand dollars")
1000 sqft house prediction 300.0 Thousand dollars
1200 sqft house prediction 340.0 Thousand dollars
2000 sqft house prediction 500.0 Thousand dollars
标图
您可以通过在成本 (w,b) 的等值线上绘制迭代的成本来显示梯度下降在执行期间的进度。
fig, ax = plt.subplots(1,1, figsize=(12, 6))
plt_contour_wgrad(x_train, y_train, p_hist, ax)
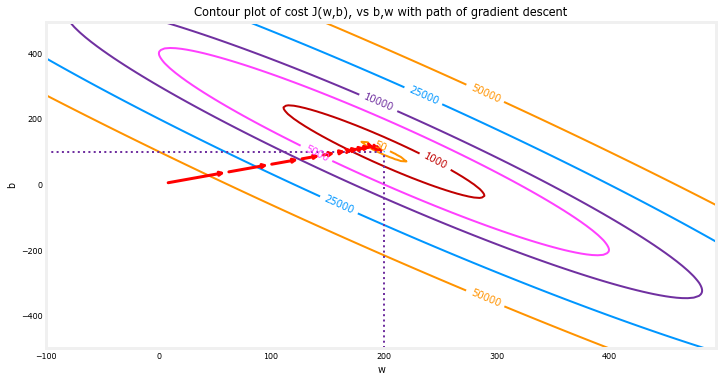
上面的等高线图显示了????(?,?)在? 和?上。
成本水平由圆环表示。使用红色箭头叠加的是渐变下降的路径。以下是一些需要注意的事项
这条道路朝着目标稳步(单调)前进。
初始步骤比目标附近的步骤要大得多。
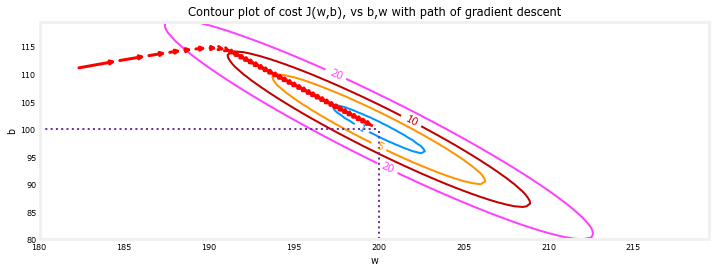
放大,我们可以看到梯度下降的最后步骤。请注意,当梯度接近零时,步长之间的距离会缩小。
fig, ax = plt.subplots(1,1, figsize=(12, 4))
plt_contour_wgrad(x_train, y_train, p_hist, ax, w_range=[180, 220, 0.5], b_range=[80, 120, 0.5],
contours=[1,5,10,20],resolution=0.5)
提高学习率 ?
有一个关于学习率的适当值的讨论,?在方程(3)中。
较大的?即,梯度下降速度越快,将收敛到一个解。但是,如果它太大,梯度下降就会发散。
试着增加?
# initialize parameters
w_init = 0
b_init = 0
# set alpha to a large value
iterations = 10
tmp_alpha = 8.0e-1
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,
iterations, compute_cost, compute_gradient)
Iteration 0: Cost 2.58e+05 dj_dw: -6.500e+02, dj_db: -4.000e+02 w: 5.200e+02, b: 3.20000e+02
Iteration 1: Cost 7.82e+05 dj_dw: 1.130e+03, dj_db: 7.000e+02 w: -3.840e+02, b:-2.40000e+02
Iteration 2: Cost 2.37e+06 dj_dw: -1.970e+03, dj_db: -1.216e+03 w: 1.192e+03, b: 7.32800e+02
Iteration 3: Cost 7.19e+06 dj_dw: 3.429e+03, dj_db: 2.121e+03 w: -1.551e+03, b:-9.63840e+02
Iteration 4: Cost 2.18e+07 dj_dw: -5.974e+03, dj_db: -3.691e+03 w: 3.228e+03, b: 1.98886e+03
Iteration 5: Cost 6.62e+07 dj_dw: 1.040e+04, dj_db: 6.431e+03 w: -5.095e+03, b:-3.15579e+03
Iteration 6: Cost 2.01e+08 dj_dw: -1.812e+04, dj_db: -1.120e+04 w: 9.402e+03, b: 5.80237e+03
Iteration 7: Cost 6.09e+08 dj_dw: 3.156e+04, dj_db: 1.950e+04 w: -1.584e+04, b:-9.80139e+03
Iteration 8: Cost 1.85e+09 dj_dw: -5.496e+04, dj_db: -3.397e+04 w: 2.813e+04, b: 1.73730e+04
Iteration 9: Cost 5.60e+09 dj_dw: 9.572e+04, dj_db: 5.916e+04 w: -4.845e+04, b:-2.99567e+04
以上 ?和 ?在正负之间来回跳动,绝对值随着每次迭代而增加。此外,每次迭代 ∂?(w,b)∂w 变化标志和成本正在增加而不是减少。这是一个明显的迹象,表明学习率太大,解决方案正在发散。
plt_divergence(p_hist, J_hist,x_train, y_train)
plt.show()
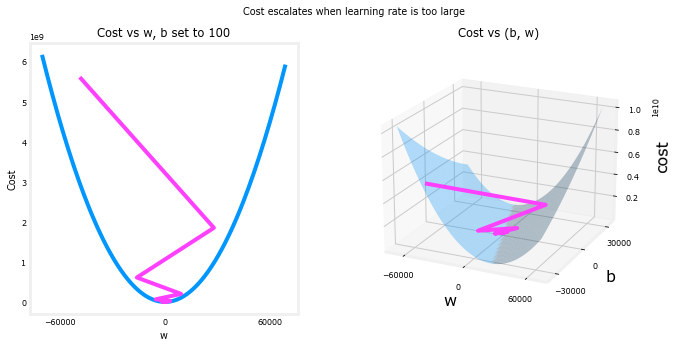
上图,左图显示 ?梯度下降的前几步的进展。?从正向负振荡,成本快速增长。梯度下降在两者上运行?和 ?
同时,因此需要右侧的3D图才能获得完整的图片。