使用
kaggle比赛中的公开数据IceCreamData数据来完成温度和销售利润的线性关系。本实例使用python来仿真实现。
1. 下载数据,IceCreamData需要注册和下载到本地。大体背景是你拥有一家冰淇淋公司,你想创建一个模型,可以根据外部空气温度(度)预测每天的收入。
2. 导入数据
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
jtplot.style(theme='grade3',context='notebook',ticks=True,grid=False)
sales_df = pd.read_csv('yourpath/IceCreamData.csv')
sales_df.shape
3. 分析数据
拿到数据之后,首先需要对数据进行理解和分析,可视化是较为有效的技术手段。当然一些基本的统计或者观察也不可缺少。
- 查看数据基本信息
sales_df.info()

- 查看数据统计值
sales_df.describe() # 查看数据的一些统计信息,如最大、最小、均值、反差
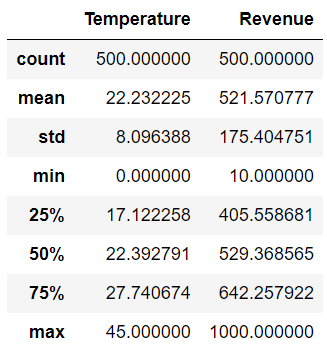
- 查看数据:可视化看散点分布
plt.figure(figsize=(13,7))
sns.scatterplot(x='Temperature',y='Revenue',data=sales_df) #绘制散点图
plt.grid()
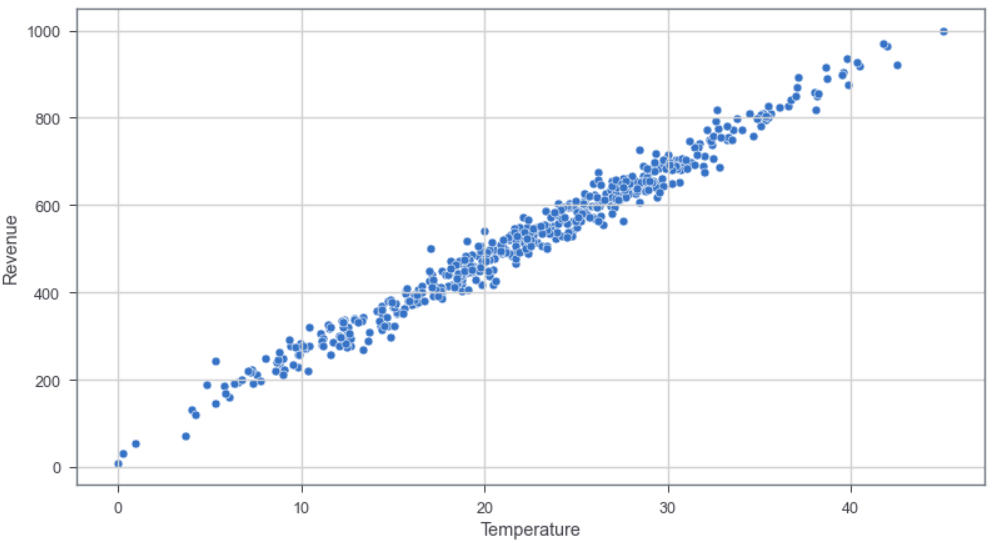
- 查看数据:可视化看散点分布与正态分布图
sns.jointplot(x='Temperature',y='Revenue',data=sales_df)
plt.grid()

- 查看数据:可视化散点图与正态分布图
sns.pairplot(sales_df)
plt.rcParams['font.sans-serif']=['SimHei']
plt.grid()
plt.suptitle('散点图和正态分布图',fontsize=20)

- 查看数据:使用直线拟合可视化
plt.figure(figsize=(13,7))
sns.regplot(x='Temperature',y='Revenue',data=sales_df)
plt.grid()
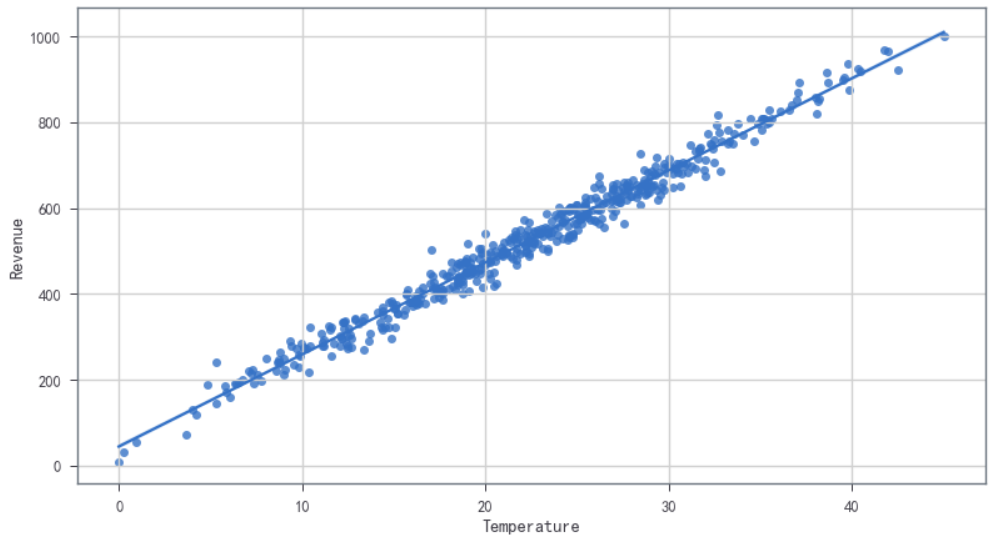
小结:从上述的数据查看可视化,数据分析看,线性回归模型就能以后不错的回归效果
4. 数据处理和线性回归模型建模
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X = sales_df['Temperature']
y = sales_df['Revenue']
X = np.array(X) # 将pandas的series类型转化为Numpy的Array(数组)
y = np.array(y)
X = X.reshape(-1, 1) # 将X数组重新构建为500行,1列
y = y.reshape(-1, 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2) #训练集和测试集的分割
SimpleLinearRegression = LinearRegression(fit_intercept=True)
SimpleLinearRegression.fit(X_train, y_train)
print('Linear Model Coeff(m)%.2f'%SimpleLinearRegression.coef_)
print('Linear Model Coeff(b)%.2f'%SimpleLinearRegression.intercept_)
获得了m值和b值,即斜率是21.44,截距是45.66
- 对训练集的数据,可视化温度和销售收入之间的回归曲线
# 得到散点图
plt.scatter(X_train, y_train, color='green')
# 得到预测的销售收入,与实际温度之间的线性回归曲线
plt.plot(X_train, SimpleLinearRegression.predict(X_train),color='blue')
# 设置x,y坐标轴的名称
plt.ylabel('Revenue[$]')
plt.xlabel('Temperature[DegC]')
# 设置图形标题
plt.title('Revenue Generated vs. Temperature')

- 查看训练集的温度和销售收入的相关系数
accuracy_LinearRegression = SimpleLinearRegression.score(X_train,y_train)
accuracy_LinearRegression
结果:0.9792858307245188
- 查看测试集的温度与销售收入的回归关系
plt.scatter(X_test,y_test,color='red')
plt.plot(X_test, SimpleLinearRegression.predict(X_test),color='blue')
plt.ylabel('Revenue[$]')
plt.xlabel('Temperature[DegC]')
plt.title('Revenue Generated vs. Temperature')

- 查看测试数据集的温度与销售收入的相关系数
pre_LinearRegression = SimpleLinearRegression.score(X_test,y_test)
pre_LinearRegression
结果:0.9808887231054377
5. 线性回归模型的优劣分析
import statsmodels.api as sm
X2 = sm.add_constant(X_train)
est = sm.OLS(y_train, X2).fit()
print(est.summary())
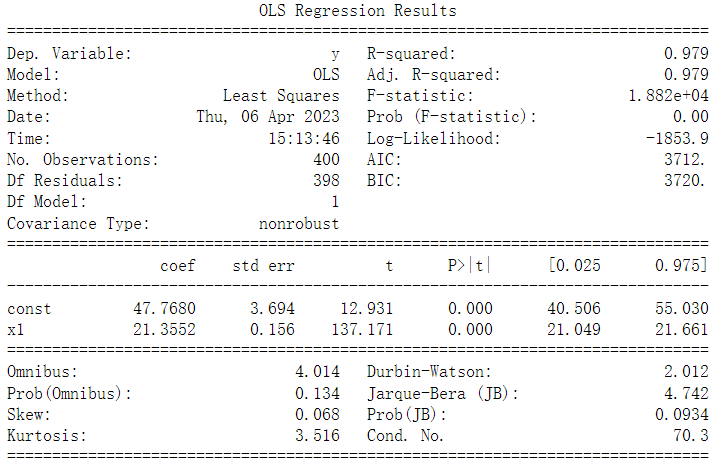
对于模型评估而言,通常需要关心上图中的R-squared、Adj.R-squared和P值信息。这里的R-squared为0.979,Adj.R-squared为0.979,
说明模型的线性拟合程度较高;这里的P值有两个,常数项(const)和特征变量(温度)的P值都约等于0<0.05,所以这两个变量都和目标变量(收入)显著相关,
即真的具有相关性,而不是由偶然因素导致的。
对于上图的参数的一些详细解释
- Dependent variable(因变量):因变量是依赖其他变量的变量。在这里
y是因变量,y依赖x。 - Model(模型):最小二乘法是使用最为广泛的方法。该模型给出了真实总体回归线的最佳近似。OLS的原理是最小化误差的平方\(argmin \sum e_{i}^{2}\)
- Number of observations(样本数):观察的次数就是样本的大小
- Degree of freedom(df) of residuals(残差自由度):自由度是计算平方和所依据的独立观测的数量。
D.f Residuals = 400 - 1 - 1 = 398, Degrees of freedom, D.f = N – K, N为样本数,K为变量数 + 1 - Df of model: 模型自由度,
Df of model = K – 1 = 2 – 1 = 1 - Constant term: 常数项是回归线的截距
y = mx + b中的b - Coefficient term:系数项表示
y的变化与X的单位变化,即如果X上升1个单位,则y上升21.3552。 - Standard error of parameters:标准误差也称为标准偏差。标准误差显示了这些参数的抽样可变性。
截断参数的标准误差:\(se(b_{1}) = \sqrt{(\frac{\sum x_{i}^{2}}{n\sum (x_{i}-\bar{x} )^{2}} )\sigma ^{2}}\)
系数项(斜率)标准误差:$se(b_{2}) = \sqrt{\frac{\sigma^{2} }{\sum (x_{i} - \bar{x} ) } } $, \(\sigma^{2}\)为回归标准误差(SER),且\(\sigma^{2}\)等于剩余平方和(Residual Sum Of Square,RSS,就是\(\sum e_{i}^{2}\)) - t – statistics: 理论上,我们假设误差项服从正态分布,因此参数\(b_{1}\)和\(b_{2}\)也具有正态分布。
- \(b_{1} \sim N(B_{1}, \sigma_{b1}^{2})\)
- \(b_{2} \sim N(B_{1}, \sigma_{b2}^{2})\) \(B_{1}\)和\(B_{2}\)分别为\(b_{1}\)和\(b_{2}\)的均值
t-统计的计算根据以下假设: - \(H_{0}:B_{2} = 0\) 变量
X对y没影响 - \(H_{1}:B_{2} \ne 0\) 变量
X对y有影响
计算t-统计:
\(t = (b_{1} - B_{1})/se(b_{1})\)
对于上面的汇总表格,\(b_{1} = 47.7680\),\(se(b_{1}) = 3.694\), 因此\(t = (47.7680 - 0)/3.694 = 12.931\),类似地,可以计算\(b_{2}\)的t-统计 = 137.171
p – values: 理论上,我们读到p值是获得t统计量至少与H0相矛盾的概率,因为假设零假设是正确的。在汇总表中,我们可以看到两个参数的p值都等于0。
这不是确切的0,但由于我们有非常大的统计量(12.931和137.171)p-value将近似为0。- Confidence intervals:有很多方法来检验这个假设,包括上面提到的
p值方法。置信区间法就是其中之一。5%是得出C.I.的标准显著性水平(\(\propto\))。\(B_{1}\)的置信区间是\((b_{1}-t_{\propto /2}se(b_{1}), b_{1}+t_{\propto /2}se(b_{1}))\)。通过查表计算\(b_{1}\)置信区间是(40.506 ,55.030),同理可以得到\(b_{2}\)的置信区间。 - R – squared value: \(R^{2}\)是决定系数,它告诉我们自变量可以解释多少百分比的变化。这里,\(y\)的97.9%的变化可以用
x来解释,\(R^{2}\)的最大可能值可以是1,意味着\(R^{2}\)值越大回归效果越好。 - F – statistic:
F检验表示回归的拟合优度。这个检验类似于t检验或我们对假设做的其他检验。F统计量的计算方法如下:
\(F = \frac{R^{2}/(k-1)}{(1-R^{2})/(n-k}\),带入\(R^{2}\), \(n\), \(k\), \(F = (0.979/1)/(0.021/398) = 1.882e+04\)
6. 线性回归模型的预测
给定温度值,得到销售收入值
Temp = np.array([37])
Temp = Temp.reshape(-1,1)
Revenue = SimpleLinearRegression.predict(Temp)
print('Revenue Prediction = ',Revenue)
Revenue Prediction = [[837.90987079]]
即给定37度,得到837.91的销售收入。