yo 大家早上好、中午好、晚上好、凌晨好
欢迎来到本篇文章
简介
本文主要解决图上定距离点对查询的问题,此算法主要运用关系矩阵、矩阵快速幂、位运算,能以近 \(O(n^2\log{n})\) 的复杂度查找出所有存在距离为 \(n\) 的路径的点对,并支持多次询问。
算法解释
关系矩阵
关系矩阵(matrix of a relation) 是对关系的一种刻画,即对于两个集合之间的某个关系,能清楚地表明此二集合的任意元素是否有此关系的数字矩阵。
关系矩阵是离散数学中的一个术语,其作用是为表示二元关系的一种方式,其外还有集合表达式和关系图可以用于表示二元关系。这里主要是利用了关系矩阵和关系图的关系,用邻接矩阵表示有向图(无向图可将边视为双向边)。在关系矩阵中用 \(M_{i, j} = 1\) 表示 \(<i, j>\) 这一有序对存在,在关系图上表示为一条从 \(i\) 连到 \(j\) 的有向边,如二元关系:
可用关系图表示为:
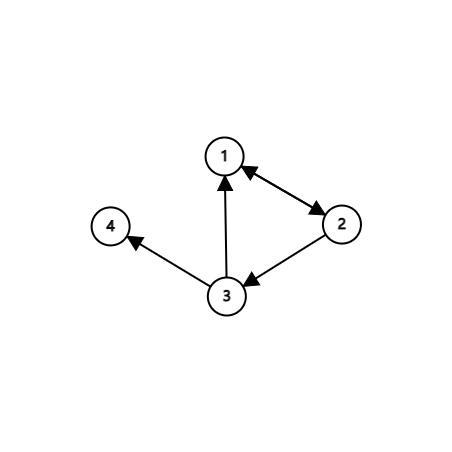
而用关系矩阵则表示为:
没错,此时我们已经用只有0和1的邻接矩阵表示了一个有向图,而这是这个算法思想的基础。
矩阵快速幂
上面用了一个邻接矩阵表示了有向图上所有距离为1的点对,包括 \(1 \to 2, 2 \to 1, 2 \to 3, 3 \to 4\), 而下面我们便可以利用矩阵乘法将其转化成表示距离为 \(n\) 的点对的矩阵
设 \(R\) 与 \(S\) 都为一个二元关系。\(R\) 和 \(S\) 的合成记作 \(R \circ S\),其定义为 \(R \circ S = \{ <x, y> \mid \exists t( <x, t> \in R \wedge <t, y> \in S)\),称为 \(S\) 对 \(R\) 的右复合。
离散数学中可用 \(R^n\) 表示二元关系 \(R\) 对自身的多次右复合,由右复合的定义可递推得出矩阵 \(R\) 的 \(n\) 次幂 \(R^n\) 可表示图上距离为 \(n\) 的点对集合。
则我们目标的矩阵 \(M\) 可用矩阵快速幂由初始邻接矩阵,即关系矩阵 \(R\) 算出。矩阵快速幂的代码这里就省略了,上面图中距离为6的点对最终算出矩阵 \(M = R^6\) 为:
位运算优化
一般的矩阵乘法大都要用到三层嵌套循环,其复杂度本身已经为 \(O(n^3)\),相比之下还不如Floyd算法。
可观察到上面矩阵包含的元素其实不只0和1(此处每个元素其实表示点对间存在多少条距离为 \(n\) 的路径),而我们需要确定的仅是确认是点对间是否存在定距离的路径,只需要0和1。矩阵乘法的定义有 \(M_{i, j} = {\textstyle \sum_{1}^{n}} A_{i, k} \times B_{k, j}\),而初始邻接矩阵中仅有0和1,则 \(i\) 与 \(j\) 间 \(n\) 长度的路径不存在当且仅当 \(R^{n - 1}\) 中每对 \(R_{i, k}, R_{k, j}\) 均有0。
因此我们将原本用二维数组表示的邻接矩阵改为用一维数组表示。这里采用c++。
vector<unsigned LL> M(63, 0), MT(63, 0);
//MT用于存储矩阵M的转置,方便后续运算
//使用 unsigned long long 可使单个数表示的点达到64个。
这样便可以将矩阵乘法修改为矩阵位运算,整体代码如下:
/*
*日期:2023/3/30
*作者:AiHAn
*说明:此代码用于图上顶距离点对查找
*/
#include <bits/stdc++.h>
#define LL long long
#define pmm pair<vector<unsigned LL>, vector<unsigned LL> >
using namespace std;
struct edge
{
int next, to;
}edges[10005];
int i = 1;
vector<int> head(55, 0); //链式前向星存图
vector<unsigned LL> MA(63, 0), MB(63, 0); //邻接矩阵
bitset<65> b;
void add(int u, int v)
{
edges[i].to = v;
edges[i].next = head[u];
head[u] = i++;
}
//矩阵位运算
pmm matrixAnd(vector<unsigned LL> A, int size, vector<unsigned LL> AT)
{
vector<unsigned LL> res1(55, 0), res2(55, 0);
for (int j = 1; j <= size; j++)
for (int k = 1; k <= size; k++)
if (A[j] & AT[k]) //判断是否均不为0
{
res1[j] |= ((LL)1 << k); //1要用LL或unsigned LL表示,不然会变的不幸
res2[k] |= ((LL)1 << j); //同时计算转置矩阵,方便下次运算
}
return make_pair(res1, res2);
}
//矩阵快速幂,和原版矩阵快速幂差不多,不加赘述
vector<unsigned LL> qpow(vector<unsigned LL> A, int size, vector<unsigned LL> AT, LL n)
{
pmm res = make_pair(A, AT);
vector<unsigned LL> res1(55, 0);
for (int j = 1; j <= size; j++)
res1[j] |= ((LL)1 << j);
while (n)
{
if (n & 1)
res1 = matrixAnd(res1, size, res.second).first;
res = matrixAnd(res.first, size, res.second);
n >>= 1;
}
return res1;
}
unsigned main()
{
int n, m, u, v, l; //n为节点数,m为边数,l为目标距离
cin >> n >> m >> l;
for (int i = 0; i < m; i++)
{
cin >> u >> v;
add(u, v);
MA[u] |= ((LL)1 << v); //初始邻接矩阵
MB[v] |= ((LL)1 << u); //初始邻接矩阵的转置
}
vector<unsigned LL> A = qpow(MA, n, MB, l);
for (int j = 1; j <= n; j++) //输出
{
b = A[j];
for (int k = 1; k <= n; k++)
cout << b[k] << " ";
cout << "\n";
}
}
输入 #1:
4 5 3
1 2
2 1
2 3
3 1
3 4
输出 #1:
1 1 0 1
1 1 1 0
1 0 1 0
0 0 0 0
输入 #2:
4 5 6
1 2
2 1
2 3
3 1
3 4
输出:
1 1 1 1
1 1 1 1
1 1 1 1
0 0 0 0
高精度处理
上面仅使用单个 unsigned long long 数表示原邻接矩阵的一行,因此最多只能表示仅有64个节点的图,节点增多的话要写高精度。但由于涉及的运算仅有与运算和或运算,这里的高精度会比较容易写。代码如下:
vector<unsigned LL> operator & (vector<unsigned LL>& l, vector<unsigned LL>& r)
{
vector<unsigned LL> res(10, 0);
for (int i = 0; i < 10; i++)
res[i] = l[i] & r[i];
return res;
}
vector<unsigned LL> operator | (vector<unsigned LL>& l, vector<unsigned LL>& r)
{
vector<unsigned LL> res(10, 0);
for (int i = 0; i < 10; i++)
res[i] = l[i] | r[i];
return res;
}
而 num |= (LL)1 << k 等可改为 num[k % maxlength] = num[k % maxlength] | ((LL)1 << (k / maxlength)) 进行处理。
应用
luogu P1613
题意
给定一张边权均为 1 的有向图,图上距离为2的幂次的点对间可连一条长度也为 1 的边,求节点 1 到 \(n\) 的最短路径长度。
解答
由于数据范围为 \(n \le 50\),题解中大多都使用 Floyd + 倍增 这种 \(O(n^3\log{maxlongint})\) 的做法。这里我们用前文的算法来解决这道题,在进行快速幂时每次位运算后遍历一次矩阵,若 \(M_{i, j}\) 为 1 就添加边,最后用 Dijstra 或 SPFA 等最短路算法求最短路即可 虽然这里作者用了最普通的BFS。最后时间复杂度仅为大概 \(O(2n^2\log{maxlongint})\)。
下附AC代码。
代码
#include <bits/stdc++.h>
#define LL long long
#define pmm pair<vector<unsigned LL>, vector<unsigned LL> >
using namespace std;
struct edge
{
int next, to;
}edges[10005]; //链式前向星存图
int i = 1, n;
vector<int> head(55, 0), vis(55, 1), cur(55, (int)1e9);
vector<vector<int> > evis(55, vector<int>(55, 1));
vector<unsigned LL> MA(55, 0), MAT(55, 0);
queue<int> q;
bitset<55> b;
void add(int u, int v)
{
edges[i].to = v;
edges[i].next = head[u];
head[u] = i++;
}
//矩阵位运算
pmm matrixAnd(vector<unsigned LL> A, int size, vector<unsigned LL> BT)
{
vector<unsigned LL> res1(55, 0), res2(55, 0);
for (int j = 1; j <= size; j++)
for (int k = 1; k <= size; k++)
if (A[j] & BT[k])
{
res1[j] |= ((LL)1 << k);
res2[k] |= ((LL)1 << j);
}
return make_pair(res1, res2);
}
//倍增
void qpow(vector<unsigned LL> A, int size, vector<unsigned LL> AT, LL N)
{
pmm res = make_pair(A, AT);
for(int j = 1; j <= N; j++)
{
res = matrixAnd(res.first, size, res.second);
for (int k = 1; k <= size; k++) //每次乘方后遍历一次矩阵,添加新边
for (int l = 1; l <= size; l++)
if (evis[k][l] && (res.first[k] & ((LL)1 << l)))
{
add(k, l);
evis[k][l] = 0;
}
}
}
void bfs(int p)
{
if (p == n)
{
cout << cur[p];
return;
}
for (int j = head[p]; j; j = edges[j].next)
if (vis[edges[j].to])
{
cur[edges[j].to] = min(cur[edges[j].to], cur[p] + 1);
q.push(edges[j].to);
vis[edges[j].to] = 0;
}
q.pop();
if (!q.empty())
bfs(q.front());
}
unsigned main()
{
int m, u, v;
cin >> n >> m;
for (int i = 0; i < m; i++)
{
cin >> u >> v;
if (evis[u][v]) //去除重边降低BFS以时间复杂度
{
add(u, v);
evis[u][v] = 0;
MA[u] |= ((LL)1 << v);
MAT[v] |= ((LL)1 << u);
}
}
qpow(MA, n, MAT, 31);
q.push(1);
vis[q.front()] = 0;
cur[q.front()] = 0;
bfs(q.front());
}
此算法纯属个人在离散课上忽然蹦出的想法
本文如有错误,还请大佬指正。