二维坐标系变换
- 由旋转角进行坐标系转换
- 构造旋转矩阵
  - 正交矩阵概念
  - 利用正交矩阵构造旋转矩阵
三维坐标系变换
小结

将对象的描述从一个坐标系转换到另一个坐标系，在图形应用非常重要。本文主要从坐标的角度，探讨二维、三维空间下的对象如何从一个坐标系转换到另一个坐标系。

非笛卡尔坐标系，有极坐标、球面坐标、椭圆坐标坐标等。这里仅考虑笛卡尔坐标系。

二维坐标系变换

由旋转角进行坐标系转换

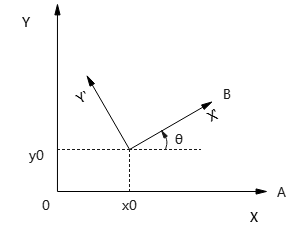
如下图，二维空间下，有2个坐标系：A为xy坐标系，B为x'y'坐标系。其中，xy坐标系原点\((0,0)\)，将其绕原点逆时针旋转θ角，然后平移到\((x_0,y_0)\)处，得到x'y'坐标系。

问题：现在A坐标系下的任一点\(P(x,y)\)，如何转换到B坐标系下的点\(P'(x', y')\)？

要求两者的转换关系，需分两步得到转换矩阵：

将x'y'系统的坐标原点\((x_0,y_0)\)平移到xy系统的原点\((0,0)\)；
将x'轴顺时针旋转θ角，到x轴上。

步骤1对应平移变换矩阵：

\[\tag{1} T(-x_0,-y_0)=\begin{bmatrix} 1 & 0 & -x_0\\ 0 & 1 & -y_0\\ 0 & 0 & 1 \end{bmatrix} \]

步骤2对应旋转变换矩阵：

\[\tag{2} R(-\theta)=\begin{bmatrix} \cos\theta & \sin\theta & 0\\ -\sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{bmatrix} \]

注意：顺时针旋转，需要取\(-\theta\)。

xy系统转换到x'y'系统的复合变换矩阵：

\[\tag{3} \begin{aligned} M_{xy,x'y'}&=R(-\theta)\cdot T(-x_0,-y_0)\\ &= \begin{bmatrix} \cos\theta & \sin\theta & 0\\ -\sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -x_0\\ 0 & 1 & -y_0\\ 0 & 0 & 1 \end{bmatrix} \\ &=\begin{bmatrix} \cos\theta & \sin\theta & -(x_0\cos\theta+y_0\sin\theta)\\ -\sin\theta & \cos\theta & x_0\sin\theta-y_0\cos\theta\\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

这样，xy系统下的坐标就能通过平移变换、旋转变换而得到x'y'下的坐标。

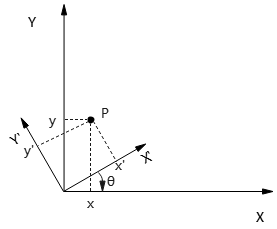
如何理解坐标轴的复合变换？

思考：明明xy坐标轴变换成了x'y'坐标轴，为什么是x'y'坐标系统转换成x'y'系统，而不是反过来？

考虑最简单的点(0,0)来验证。假设x'y'系统下，原点坐标\((0,0)^B\)，那么其在xy系统下坐标为\((x_0,y_0)^A\)，显然不符合复合转换矩阵；
而xy系统下原点\((0,0)^A\)，在x'y'系统下，坐标为\((-(x_0\cos\theta+y_0\sin\theta),x_0\sin\theta-y_0\cos\theta)^B\)，符合转换矩阵。（可考虑特殊情况，\(\theta={\pi\over 4}, x_0=y_0=1\)）

可以这样理解，将x'y'坐标轴变换到xy坐标轴的位置后，就只用关心P点在新坐标系统下的位置。如下图所示，经过复合变换，将xy系统下点\(P(x_p,y_p)^A\)转换到x'y'系统下的点\(P'(x_p',y_p')^B\)。

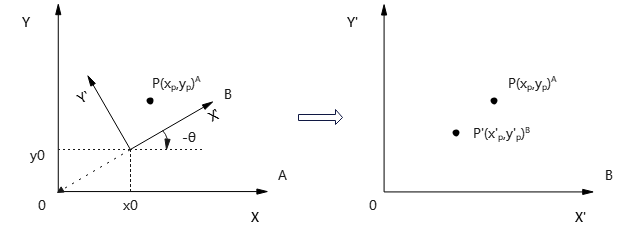
变换过程：

\[P'(x_p',y_p')^B=M_{xy,x'y'}P(x_p,y_p)^A=R(-\theta)\cdot T(-x_0,-y_0)\cdot \begin{bmatrix} x_p\\y_p\\1 \end{bmatrix}^A \]

如果令\(x=x_p, y=y_p, x'=x_p', y'=y_p'\)，
那么，

\[\tag{4} P'(x',y')^B=R(-\theta)\cdot T(-x_0,-y_0)\cdot P(x,y)^A \]

这样，就将xy系统下的坐标转换到了x'y'系统。

构造旋转矩阵

有时，我们并不知道旋转角θ具体是多少，而知道新的坐标轴方向（x'或y'轴）。此时，可以先求θ角大小（向量点积），然后得到旋转矩阵；这里要介绍的是另一种方法：构造旋转矩阵，将坐标轴x'y'旋转到坐标轴xy。

正交矩阵概念

先复习几个概念：

正交向量

点积为0的两个或多个向量，称为正交向量。

假设向量\(V_1=(x_1,y_1), V_2=(x_2,y_2)\)是一组正交向量，则\(V_1\cdot V_2=x_1x_2+y_1y_2=0\)。
所谓正交向量，

正交矩阵

如果矩阵A，满足\(A^TA=E\)，则称A为正交矩阵。

对于正交矩阵，其行向量组（或列向量组）为单位向量且两两正交。这组列向量构成一个空间的基，称为规范正交基。
下面证明：
设A是一个列向量矩阵且为正交矩阵，\(A=(\alpha_1,\alpha_2,...,\alpha_n)\)，其中\(\alpha_i(i=1,2,...,n)为列向量\)，那么，

\[\begin{aligned} A^TA=\begin{bmatrix} \alpha_1^T\\ \alpha_2^T\\ ... \alpha_n^T \end{bmatrix} \begin{bmatrix} \alpha_1,\alpha_2,...,\alpha_n \end{bmatrix}&=E\\ \begin{bmatrix} \alpha_1^T\alpha_1 & \alpha_1^T\alpha_2 & ... & \alpha_1^T\alpha_n\\ \alpha_2^T\alpha_1 & \alpha_2^T\alpha_2 & ... & \alpha_2^T\alpha_n\\ ... & ... & ... & ...\\ \alpha_n^T\alpha_1 & \alpha_n^T\alpha_2 & ... & \alpha_n^T\alpha_n \end{bmatrix}&=\begin{bmatrix} 1 & 0 & ... & 0\\ 0 & 1 & ... & 0\\ ... & ... & ... & ...\\ 0 & 0 & ... & 1 \end{bmatrix} \end{aligned} \]

对于任意列向量\(\alpha_i,\alpha_j\)，
1）如果i=j，那么\(\alpha_i*\alpha_j=\alpha_i*\alpha_i=1\)，也就是说，\(\alpha_i\)与自身的内积为1，即列向量\(\alpha_i\)为单位向量。
2）如果i≠j，那么\(\alpha_i*\alpha_j=0\)，则列向量\(\alpha_i, \alpha_j\)互为正交向量。

当A由行向量组成时，该结论依然成立。

利用正交矩阵构造旋转矩阵

已知+y'轴方向的向量V。如下图所示，可将V指定为xy系统下相对于原点的一个向量。那么，y'方向的单位向量v：

\[\tag{5} v={V\over |V|}=(v_x,v_y)^A \]

将v顺时针旋转90°，得到沿x'轴的单位向量u：

\[\tag{6} \begin{aligned} u&=(u_x,u_y)\\ &=(v_y,-v_x) \end{aligned} \]

上式证明：
如下图所示
∵v, u都是单位向量
∴|v|=|u=1
假设v在第二象限，v与y轴夹角为α，
那么，向量v坐标(-cosα, sinα)，向量u坐标(sinα,cosα)
现将v写成(vx,vy)，那么u=(vy,-vx)，即得证。

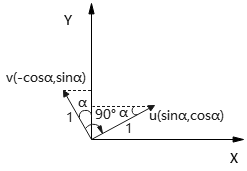
显然，向量v、u正交，有vu=0，即v⊥u。

由式(2)，我们知道，旋转矩阵\(R(-\theta)\)的行向量是一组正交单位向量（严格来说，是一组规范正交基）：

\[R(-\theta)=\begin{bmatrix} \cos\theta & \sin\theta & 0\\ -\sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{bmatrix} \\ 向量组(\cos\theta, \sin\theta, 0),(-\sin\theta,\cos\theta,0),(0,0,1)是一组规范正交基 \]

问题来了，我们是否可以由一组规范正交基得到对应旋转矩阵呢？
答案是可以的，可以用规范正交基作为行向量（或列向量）构造出旋转矩阵。不妨令，

\[\tag{7} R=\begin{bmatrix} u_x & u_y & 0\\ v_x & v_y & 0\\ 0 & 0 & 1 \end{bmatrix} \]

其中，\(v_x=-\sin\theta,v_y=\cos\theta\)。利用式(6) u和v的关系，可以得到，\(u_x=v_y=\cos\theta, u_y=-v_x=\sin\theta\)，这符合旋转矩阵\(R(-\theta)\)特性。

接下来，问题是\(\theta\)在[0,2π)范围内是否有唯一解？这样，构造出的旋转矩阵就能对应一个唯一的旋转。
答案是有唯一解。下面证明：
我们知道，正弦和余弦函数在0~2π范围内有2个解（如果有解），设2个解分别为\(\theta1,\theta2\)，范围都是\([0,2\pi)\)。
先根据\(\sin\theta\)讨论\(\theta\)取值范围，
1）当\(v_x<0\)时，\(\sin\theta>0\)，那么\(\theta1 \in [0,{\pi\over 2}), \theta2\in [{\pi\over 2}, \pi)\)；
2）当\(v_x>=0\)时，\(\sin\theta<=0\)，那么\(\theta1\in [\pi,{3\over 2}\pi), \theta2\in[{3\over 2}\pi, 2\pi)\)；

再根据\(\cos\theta\)讨论\(\theta\)取值范围，
1）当\(v_y>0\)，则\(\theta1\in[0,{\pi\over 2}),\theta2\in[{3\over 2}\pi, 2\pi)\)；
2）当\(v_y<0\)，则\(\theta1\in [{\pi\over 2},\pi),\theta2\in [\pi,{3\over 2}\pi)\)。

再综合sin、cos取值范围。不难发现，当sin、cos取值确定时，\(\theta\)范围只能是长度为π/2的4个区间之一：\([0,{\pi \over 2}), [{\pi \over 2},\pi), [\pi,{3\over 2}\pi), [{3\over 2}\pi,2\pi)\)。
而sin、cos在这些区间上是连续且单调的，因此有唯一解。

举个例子，如果对应y'轴方向的向量V=(-1,0)，那么x'轴的方向向量u应该在+y轴上（u=(0,1)），且旋转矩阵为：

\[R=\begin{bmatrix} u_x & u_y & 0\\ v_x & v_y & 0\\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

而我们根据式(2)，令\(\theta={\pi\over 2}\)，也能得到同样的旋转矩阵。

tips：这里只是得到旋转矩阵，并没有考虑平移。如果要求平移变换矩阵，还需要知道x'y'坐标原点在xy系统的位置。

三维坐标系变换

类似于二维坐标系变换，三维空间下，也能用一组规范正交基构造绕任意进行轴旋转操作的旋转矩阵。

问题描述：要将xyz系统下的坐标描述转换到x'y'z'坐标系统。
步骤：
1）先将x'y'z'原点平移到xyz原点；
2）进行一系列旋转使得对应坐标轴重合。如果2坐标系比例不同，需要先进行一次缩放变换使得比例相同。

举例，如下图所示：

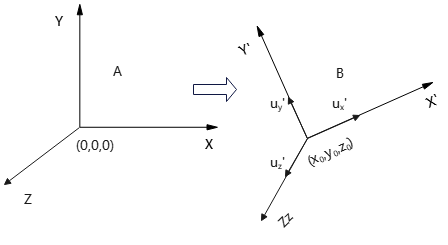
其中，\(u_x',u_y',u_z'\)分别为代表X'、Y'、Z'轴方向的单位轴向量。

x'y'z'系统（A）的原点在xyz系统（B）的\((x_0,y_0,z_0)^A\)位置，其坐标轴由xyz系统对应坐标轴旋转得到。
首先，可以用平移矩阵\(T(-x_0,-y_0,-z_0)\)将x'y'z'原点移至与xyz原点重合。
三维平移、旋转、缩放操作，参见这篇文章计算机图形：三维几何变换。

\[\tag{8} T(-x_0,-y_0,-z_0)=\begin{bmatrix} 1 & 0 & 0 & -x_0\\ 0 & 1 & 0 & -y_0\\ 0 & 0 & 1 & -z_0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

然后，用单位轴向量来构造坐标轴旋转矩阵，用于将单位轴向量\(u_x',u_y',u_z'\)分别转换到x、y、z轴上。其构造方法，类似于二维的情形（参见式(8)）。

\[\tag{9} R=\begin{bmatrix} u_{x1}' & u_{x2}' & u_{x3}' & 0\\ u_{y1}' & u_{y2}' & u_{y3}' & 0\\ u_{z1}' & u_{z2}' & u_{z3}' & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]

注意：这里3个单位轴向量\(u_x'=(u_{x1}',u_{x2},u_{x3}'), u_y'=(u_{y1}',u_{y2}',u_{y3}'), u_z'=(u_{z1}',u_{z2}',u_{z3}')\)，其坐标为A系统下的坐标。

于是，我们得到了完整的坐标变换复合矩阵：

\[\tag{10} M_{xyz,x'y'z'}=R\cdot T(-x_0,-y_0,-z_0) \]