常用损失函数

目录

• 损失函数的意义
• 均方误差(MSE)
  • 计算方法
  • 适用场景
  • 代码
• 均方根误差(RMSE)
  • 计算方法
  • 使用场景
  • 代码
• 平均绝对误差(MAE)
  • 计算方法
  • 适用场景
  • 代码
• 交叉熵损失
  • 计算方法
  • 适用场景
  • 代码
• 对数似然损失
  • 计算方法
  • 适用场景
  • 代码
• 余弦相似度损失(CSL)
  • 计算方法
  • 推理过程
  • 适用场景
  • 代码
• Kullback-Leibler散度(KL散度)
  • 计算方法
  • 适用场景
  • 代码
• Huber损失
  • 计算方法
  • 推理过程
  • 适用场景
  • 代码
• Hinge损失
  • 计算方法
  • 适用场景
  • 代码

损失函数的意义

1. 衡量模型性能。损失函数提供了一种量化模型预测结果与实际结果之间差异的方法。通过这种量化，我们可以客观地评价模型的好坏。
2. 模型优化的指导。模型训练实际上是一个优化过程，目的是最小化损失函数。
3. 模型选择和调整。不同的问题可能更适合不同的损失函数。
4. 处理不平衡数据。在现实世界的数据中，常出现数据不平衡的情况。如分类问题中某些类别的样本数量远大于其他类别。特定的损失函数(如加权交叉熵)可以帮助模型更好地处理这种不平衡，提高模型在较少样本类别上的性能。
5. 防止过拟合。某些损失函数(如L1和L2正则化)包含了惩罚项，用于控制模型复杂度，避免过拟合。
6. 影响模型的学习方式。不同的损失函数对模型的影响方式不同。如：Huber损失对离群点的敏感度较低，可以使模型在面对异常值时更加鲁棒。

均方误差(MSE)

均方误差用于衡量模型的预测值与真实值之间的差异。MSE适用于回归问题，旨在最小化模型的预测误差。

计算方法

假设我们有一个包含n个样本的数据集，其中每个样本的真实值为\(y_{i}\),模型的预测值为\(\widehat{y}_{i}\),则均方误差的计算方法如下：

适用场景

均方误差通常用于回归问题，其中模型的目标是预测持续数值输出。均方误差对异常值敏感，因为它对差异的平方进行了求和，因此在使用MSE时需要注意异常值的处理。

代码

import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
true_values = np.array([2, 4, 5, 7, 8])
predicted_values = np.array([1.5, 3.5, 5.2, 6.8, 8.5])

# 计算均方误差
mse = np.mean((predicted_values - true_values) ** 2)

# 绘制数据点
plt.scatter(true_values, predicted_values, label='Data points')

# 绘制直线 y=x，表示完美预测
plt.plot([0, 10], [0, 10], linestyle='--', color='red', label='Perfect Prediction')

# 添加均方误差信息
plt.text(1, 8, f'MSE = {mse:.2f}', fontsize=12, color='blue')

# 设置图表标签
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.title('Mean Squared Error (MSE)')
plt.grid(True)

# 显示图像
plt.show()

该代码生成了一个散点图，其中x轴表示真实值，y轴标识模型的预测值。

均方根误差(RMSE)

RMSE与MSE相似，但是会在计算前会对均方误差进行平方根运算，以测量模型的预测值与真实值之间的平均偏差。

计算方法

假设我们有一个包含n个样本的数据集，其中每个样本的真实值为\(y_{i}\),模型的预测值为\(\widehat{y}_{i}\),则均方根误差的计算方式如下：

使用场景

均方根误差通常用于回归问题，特别是在希望更好地理解模型的预测误差的情况下，因为它以与原始数据相同的度量单位表示误差。与MSE不同，RMSE对误差的量级更为敏感，因此可以用于比较不同问题中模型的性能。

代码

import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
true_values = np.array([2, 4, 5, 7, 8])
predicted_values = np.array([1.5, 3.5, 5.2, 6.8, 8.5])

# 计算均方误差
mse = np.mean((predicted_values - true_values) ** 2)

# 计算均方根误差
rmse = np.sqrt(mse)

# 绘制数据点
plt.scatter(true_values, predicted_values, label='Data points')

# 绘制直线 y=x，表示完美预测
plt.plot([0, 10], [0, 10], linestyle='--', color='red', label='Perfect Prediction')

# 添加均方根误差信息
plt.text(1, 8, f'RMSE = {rmse:.2f}', fontsize=12, color='blue')

# 设置图表标签
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.title('Root Mean Squared Error (RMSE)')
plt.grid(True)

# 显示图像
plt.show()

平均绝对误差(MAE)

平均绝对误差用于回归问题中衡量模型的预测值与真实值之间的平均绝对误差。

计算方法

适用场景

平均绝对误差适用于回归问题，特别适用于数据中存在离散值的情况，因为它对异常值的影响较小。

代码

import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
true_values = np.array([2, 4, 5, 7, 8])
predicted_values = np.array([1.5, 3.5, 5.2, 6.8, 8.5])

# 计算平均绝对误差
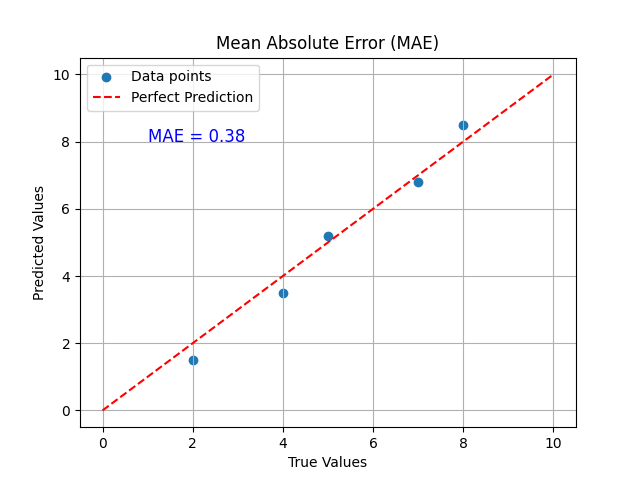
mae = np.mean(np.abs(predicted_values - true_values))

# 绘制数据点
plt.scatter(true_values, predicted_values, label='Data points')

# 绘制直线 y=x，表示完美预测
plt.plot([0, 10], [0, 10], linestyle='--', color='red', label='Perfect Prediction')

# 添加平均绝对误差信息
plt.text(1, 8, f'MAE = {mae:.2f}', fontsize=12, color='blue')

# 设置图表标签
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.title('Mean Absolute Error (MAE)')
plt.grid(True)

# 显示图像
plt.show()

交叉熵损失

计算方法

假设我们有一个包含n个样本的分类问题，每个样本属于某一类别(通常用one-hot编码表示)。上述式子中，C表示类别，\(y_{ij}\)表示第i个样本的第j个类别的真实标签，\(\widehat{y}_{ij}\)表示模型的输出概率（通常用softmax）函数处理。

适用场景

交叉熵损失通常用于分类问题，特别是多分类问题。它对模型的分类结果与真实标签之间的误差进行有效待的建模，激励模型产生更准确地分类概率分布。

代码

import numpy as np
import matplotlib.pyplot as plt

# 定义模型输出的概率分布（通常通过Softmax函数得到）
predicted_probs = np.linspace(0.01, 0.99, 100)  # 模拟从0.01到0.99的概率值
true_label = 1  # 假设真实标签为类别1

# 计算交叉熵损失
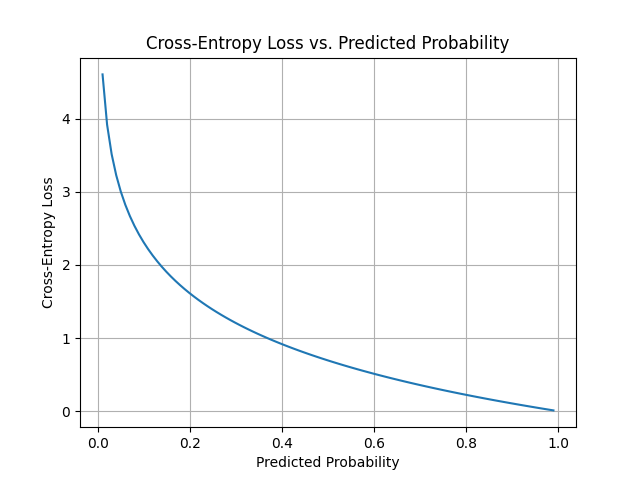
cross_entropy_loss = -np.log(predicted_probs)

# 绘制图像
plt.plot(predicted_probs, cross_entropy_loss)
plt.xlabel('Predicted Probability')
plt.ylabel('Cross-Entropy Loss')
plt.title('Cross-Entropy Loss vs. Predicted Probability')
plt.grid(True)

# 显示图像
plt.show()

对数似然损失

对数似然损失是用于分类问题的一种常见损失函数。

计算方法

适用场景

对数损失常用于分类问题，特别是二分类问题。

代码

import numpy as np
import matplotlib.pyplot as plt

# 定义模型输出的概率分布（范围在0到1之间）
predicted_probs = np.linspace(0.01, 0.99, 100)

# 计算对数损失
log_loss_positive = -np.log(predicted_probs)
log_loss_negative = -np.log(1 - predicted_probs)

# 绘制图像
plt.plot(predicted_probs, log_loss_positive, label='Log Loss (y=1)')
plt.plot(predicted_probs, log_loss_negative, label='Log Loss (y=0)')
plt.xlabel('Predicted Probability')
plt.ylabel('Log Loss')
plt.title('Log Loss vs. Predicted Probability')
plt.legend()
plt.grid(True)

# 显示图像
plt.show()

余弦相似度损失(CSL)

余弦相似度损失通常用于监督学习任务，如人脸识别、图像检索和文本相似度等，其中要最大化相似样本对的余弦相似度并最小化不相似样本对的余弦相似度。

计算方法

给定两个向量\(a\)和\(b\)，它们的余弦相似度可以表示为：

其中，\(a\cdot{b}\)表示向量$ a \(和\)b\(的内积，\)||a||\(和\)||b||\(分别表示向量\)a\(和\)b\(的范数，\)θ$表示两个向量之间的夹角。

推理过程

1. 计算两个向量\(a\)和\(b\)的内积，表示它们的相似性度量。
2. 计算两个向量\(a\)和\(b\)的范数，用于标准化相似度，使其范围在-1到1之间。
3. 将内积除以两个向量的范数，得到余弦相似度。
4. 最小化余弦相似度来使相似样本对的余弦相似度接近1，而不相似样本的余弦相似度接近-1。

适用场景

余弦相似度损失常用于以下场景：

• 人脸识别：用于度量不同人脸之间的相似性，以便于将它们分配到正确的身份。
• 图像检索：用于在图像库中查找与查询图像相似的图像。
• 文本相似度：用于衡量文本之间的相似性，如自然语言处理中的文本相似度评估。
• 推荐系统：用于度量用户与物品之间的相似性，以进行个性化推荐。

代码

余弦相似度本身不是一个损失函数，因此不容易通过图像来表示。如下是考虑绘制余弦相似度随着夹角变化的图像，来表示余弦相似度在不同夹角下的变化。

import numpy as np
import matplotlib.pyplot as plt

# 定义夹角的范围（0到π）
theta = np.linspace(0, np.pi, 100)

# 计算余弦相似度
cos_similarity = np.cos(theta)

# 绘制图像
plt.plot(theta, cos_similarity)
plt.xlabel('Angle (radians)')
plt.ylabel('Cosine Similarity')
plt.title('Cosine Similarity vs. Angle')
plt.grid(True)

# 显示图像
plt.show()

Kullback-Leibler散度(KL散度)

KL散度，也成为相对熵。是一种用于平衡两个概率分布之间差异的度量。在机器学习中，KL散度通常用于衡量两个概率分布之间的相似性或差异性。

计算方法

假设有两个概率分布\(P\)和\(Q\)，KL散度的计算方法如下：

其中，\(i\)代表概率分布中的一个事件，\(P(i)\)和\(Q(i)\)分别是事件$ i
\(在分布\)P\(和\) Q $中的概率。

适用场景

KL散度在机器学习中的许多领域都有应用，包括：

• 概率模型比较：用于比较两个概率分布，例如咋生成模型评估中
• 信息理论：KL散度是信息论中的一个重要概念，用于度量信息的差异
• 正则化：在正则化损失函数中，KL散度可以作为正则项，帮助模型更好地拟合

代码

import numpy as np
import matplotlib.pyplot as plt

# 定义两个概率分布P和Q（示例中使用均匀分布）
P = np.array([0.2, 0.3, 0.1, 0.4])
Q = np.array([0.25, 0.25, 0.25, 0.25])

# 计算KL散度
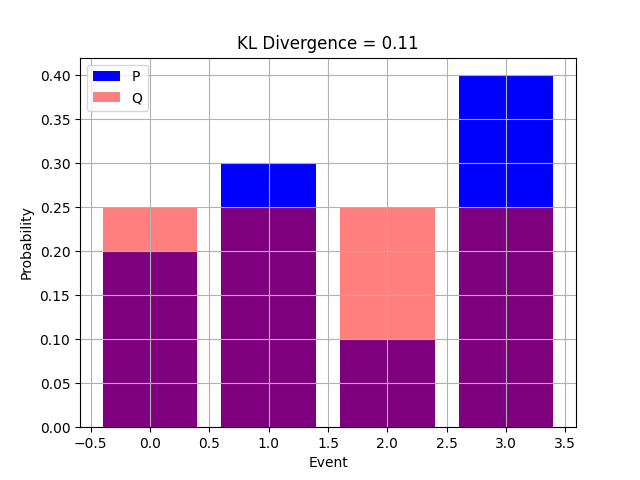
KL_divergence = np.sum(P * np.log(P / Q))

# 定义柱形的颜色
color_P = 'blue'
color_Q = 'red'

# 绘制图像
plt.bar(range(len(P)), P, label='P', color=color_P)
plt.bar(range(len(Q)), Q, alpha=0.5, label='Q', color=color_Q)
plt.xlabel('Event')
plt.ylabel('Probability')
plt.title(f'KL Divergence = {KL_divergence:.2f}')
plt.legend()
plt.grid(True)

# 显示图像
plt.show()

Huber损失

Huber损失是一种平滑的损失函数，通常用于回归问题中，以降低对异常值的敏感性。与MSE相比，Huber损失对离群点具有更好的鲁棒性，能够在一定程度上减少异常值的影响。

计算方法

其中，\(y\)是真实值，\(\widehat{y}\)是模型的预测值，\(\delta\)是Huber损失的阈值参数，通常是一个正数。

推理过程

1. 如果真实值\(y\)和模型的预测值$ \widehat{y} $之间的差异小于或等于阈值，则使用平方差的一半来计算损失
2. 如果大于阈值，则计算一个线性部分，该部分的损失以恒定的斜率增加，以减少对离群点的敏感性。

适用场景

Huber损失常用于回归问题。

代码

import numpy as np
import matplotlib.pyplot as plt

# 定义Huber损失函数
def huber_loss(y, y_hat, delta):
    absolute_error = np.abs(y - y_hat)
    if absolute_error <= delta:
        return 0.5 * (y - y_hat) ** 2
    else:
        return delta * (absolute_error - 0.5 * delta)

# 定义阈值参数
delta = 1.0

# 创建一组真实值和预测值
y_values = np.linspace(-3, 3, 400)
y_hat = 1.5  # 假设一个特定的预测值

# 计算对应的Huber损失
loss_values = np.zeros_like(y_values)
for i in range(len(y_values)):
    loss_values[i] = huber_loss(y_values[i], y_hat, delta)

# 绘制图像
plt.plot(y_values, loss_values, label=f'Prediction = {y_hat}')
plt.xlabel('True Values')
plt.ylabel('Huber Loss')
plt.title(f'Huber Loss vs. True Values (Delta = {delta})')
plt.legend()
plt.grid(True)

# 显示图像
plt.show()

Hinge损失

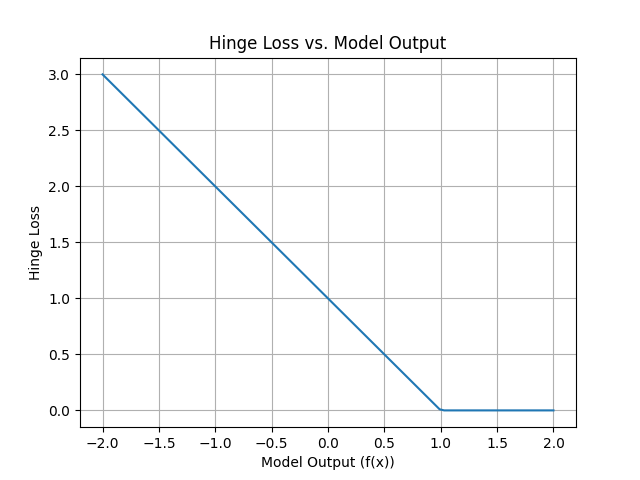
Hinge损失是SVM等分类算法的损失函数。它用于衡量模型的分类输出与真实标签之间的差异，并被设计为一种较好的分离超平面优化目标

计算方法

假设有一个包含$ n \(个样本的二分类问题，每个样本的真实标签为\)y_{i}\((通常是+1或-1），模型的分类输出为\)f(x_{i})\(,其中\)x_{i}$是输入样本。

适用场景

Hinge损失常用于SVM等二分类算法中。

代码

import numpy as np
import matplotlib.pyplot as plt

# 定义模型输出的一维特征值范围
f_x = np.linspace(-2, 2, 100)

# 计算Hinge损失
hinge_loss = np.maximum(0, 1 - f_x)

# 绘制图像
plt.plot(f_x, hinge_loss)
plt.xlabel('Model Output (f(x))')
plt.ylabel('Hinge Loss')
plt.title('Hinge Loss vs. Model Output')
plt.grid(True)

# 显示图像
plt.show()

本栏目推荐文章
• 函数的参数类型
• 【C语言】函数的递归调用
• Python教程(23)——Python类中常用的特殊成员
• NUS CS1101S：SICP JavaScript 描述：一、使用函数构建抽象
• asp.net mvc4 controller构造函数
• 函数返回值
• 50个常用的Qt开源库
• GitHub常用搜索技巧
• JS常用工具：Webpack 和 JShaman分别有什么用？
• 10-函数进阶-作用域

函数 损失 常用函数 损失 常用 函数 激活 损失 常用 函数 损失 损失 序列 函数 深度 误差 函数 损失 问题 函数 深度 损失 基础 函数 网路 神经 损失 函数 损失pytorch 函数 损失giou diou 残差 函数 损失 网络