函数、极限与连续

映射：又称为算子，一个非空集合 X 的元素按某种法则 f 与另一个非空集合 Y 的元素对应。

在映射 f 下，y称为x的像，x称为y的原像。集合X称为定义域D_f，定义域的元素的像的集合称为值域R_f。

也就是说，\(R_f \subset Y\)。

映射分为以下三种：

单射：一个x对应一个y；
满射：Y中任意元素在X中都有对应的像；
双射：既是单射也是满射。

?相关知识点?

只有单射才有逆映射。

复合映射 \((g \circ f)(x)\)，g的值域必须包含在f的定义域内，也就是说g、f的顺序是有意义的。

函数：y=f(x)。函数关系中的原像称为自变量，像称为因变量。

记号f表示x、y之间的映射法则，f(x)表示x对应的函数值。

子集：A是B的子集，记作\(A \subset B\)或 \(A \supset B\)（A包含于B，B包含A）。

自然数集 N、整数集 Z、有理数集 Q、实数集 R，\(N \subset Z \subset Q \subset R\)

集合的交差并补：

\[A \cap B ,A \setminus B ,A \cup B ,C_UA或A^C \]

补集的对偶性

\[(A \cup B)^C = A^C \cap B^C \\ (A \cap B)^C = A^C \cup B^C \]

基本初等函数

?幂函数：\(y=x^ \alpha\)（\(\alpha 是常数\)）

?指数函数：\(y=a^x\)（\(a > 0 ,a \ne 1\)）

?对数函数：\(y=log_ax\)（\(a > 0 ,a \ne 1\)）

常用对数等式

\[x = e^{ln x}\\ x^a=e^{alnx} \]

?三角函数：

y=tan x的定义域是\(\{x|x \ne \frac{\pi}{2} + k \pi，k=0，\pm 1，\pm 2 ... \}\)，值域是\((- \infty,+ \infty)\)，最小正周期是\(\pi\)，奇函数。

y=cot x的定义域是\(\{x|x \ne k \pi，k=0，\pm 1，\pm 2 ...\}\)，值域是\((- \infty,+ \infty)\)，最小正周期是\(\pi\)，奇函数。

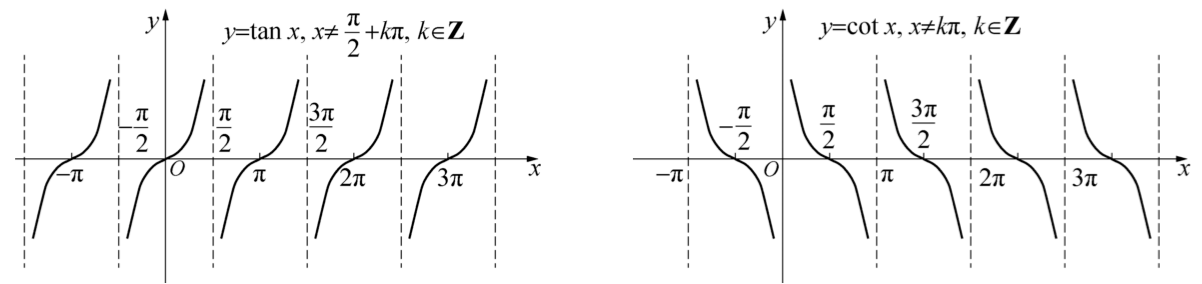
?反三角函数：

y=arcsinx的定义域是\([-1，1]\)，值域是\([-\frac{\pi}{2}，\frac{\pi}{2}]\)，称为反正弦函数。

y=arccosx的定义域是\([-1，1]\)，值域是\([0,\pi]\)，称为反余弦函数。

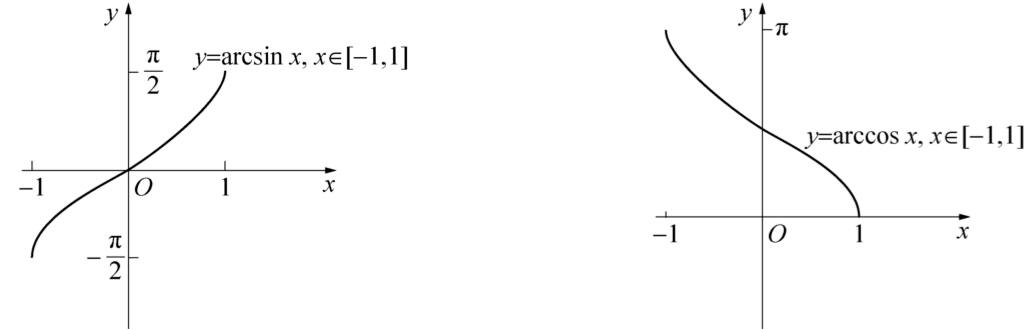
y=arctanx的定义域是\((-\infty,\infty)\)，值域是\((-\frac{\pi}{2}，\frac{\pi}{2})\)，成为反正切函数。

y=arccotx的定义域是\((-\infty,\infty)\)，值域是\((0，\pi)\)，成为反余切函数。

还有特殊函数如常数函数、绝对值函数、符号函数、取整函数。

数列极限

设\(\{x_n\}\)是一数列，如果存在某个常数\(a \in R\)，对于任意给定的正数\(\epsilon\)，总存在一个正整数N，使得对于\(n > N\)时一切n，不等式\(|x_n - a|<\epsilon\)，则称常数a是数列\(\{x_n\}\)的极限，或者称\(\{x_n\}\)收敛于a，记作

\[lim_{n \to \infty}{x_n}=a或x_n \to a(n \to \infty) \]

如果这样的a不存在，则称数列没有极限或发散。
使用简洁语言表示就是：如果\(\forall \epsilon >0，\exists N \in Z^+，当n>N时，恒有|x_n -a |<\epsilon\)，则\(lim_{n \to \infty}{x_n}=a\)。

数列极限运算法则（\(lim_{n\to \infty}{x_n}=a\)，\(lim_{n\to \infty}{y_n}=b\)）：

加减：\(lim_{n\to \infty}{(x_n\pm y_n)}=lim_{n\to \infty}{x_n}\pm lim_{n\to \infty}{y_n}=a\pm b\)
乘法：\(lim_{n\to \infty}{x_n}\cdot y_n=lim_{n\to \infty}{x_n}\cdot {y_n}=a \cdot b\)
交换：\(lim_{n\to \infty}{\sqrt{x_n}}=\sqrt{lim_{n\to \infty}{x_n}}=\sqrt{a}\)
除法：\(lim_{n\to \infty}{\frac{x_n}{y_n}}=\frac{lim_{n \to \infty}{x_n}}{lim_{n\to \infty}{y_n}}=\frac{a}{b}\)

函数极限

趋于无穷大的极限：如果\(\forall \epsilon >0，\exists X > 0，当x>X时，恒有|f(x) - A |<\epsilon\)，则\(lim_{x \to +\infty}{f(x)}=A\)。

趋于某个点的极限：\(\forall \epsilon>0，\exists \delta>0,当0<|x-x_0|<\delta时，恒有|f(x)-A|<\epsilon，那么lim_{x \to x_0}{f(x)}=A\)。

函数极限的运算与数列极限的运算类似，都有加减乘除、交换，此外还有以下法则;

\(lim_{x\to x_0}{[\alpha f(x)+ \beta g(x)]}=\alpha lim_{x\to x_0}{f(x)} + \beta lim_{x\to x_0}{g(x)}\)
\(lim_{x\to x_0}{[f(x)]^n}=[lim_{x\to x_0}{f(x)}]^n\)

复合函数的极限运算法则：

\(lim_{x\to x_0}{f[g(x)]}=lim_{x\to x_0}{f[u]}=lim_{u\to u_0}{f(u)}=f(u_0)\)

数列极限的性质

数列极限的唯一性：如果\(\{x_n\}\)收敛，则极限唯一。
数列极限的有界性：如果\(\{x_n\}\)收敛，则\(\{x_n\}\)有界。
数列极限的保号性：如果\(\{x_n\}\)收敛于a，则从某项起\(\{x_n\}\)与a同号。
推论：如果\(\{x_n\}\)收敛于a，则\(\{x_n\}\)的任意子列也收敛于a。

函数极限的性质

函数极限的唯一性：如果\(lim_{x\to x_0}{f(x)}=A\)，\(lim_{x\to x_0}{f(x)}=B\)，则A=B。
函数极限的局部有界性：如果\(lim_{x\to x_0}{f(x)}=A\)，则存在\(\delta>0\)，使得当\(0<|x-x_0|<\delta\)时，\(|f(x)|<M\)。
函数极限的局部保号性：如果\(lim_{x\to x_0}{f(x)}=A\)，且A>0，则存在\(\delta>0\)，使得当\(0<|x-x_0|<\delta\)时，\(f(x)>0\)。
函数极限的局部保号性的反推：如果存在\(\delta>0\)，使得当\(0<|x-x_0|<\delta\)时，\(f(x)>0\)，则\(lim_{x\to x_0}{f(x)}\geq 0\)。
函数极限的局部保号性的大于|A|/2的推论：如果\(lim_{x \to x_0}f(x)=A(A \ne 0)\),则存在\(\delta>0\)，使得当\(0<|x-x_0|<\delta\)时，\(|f(x)|>\frac{|A|}{2}\)。
函数极限与数列极限的关系：如果\(lim_{x\to x_0}{f(x)}=A\)，则对于任意收敛于\(x_0\)的数列\(\{x_n\}\)，有\(lim_{n\to \infty}{f(x_n)}=A\)。

两个重要极限

\(lim_{x\to 0}{\frac{sinx}{x}}=1\)
\(lim_{x\to \infty}{(1+\frac{1}{x})^x}=e\)

三角函数的相关公式和二项式定理

\(sin^2x+cos^2x=1\)
\(sin(x\pm y)=sinxcosy\pm cosxsiny\)
\(cos(x\pm y)=cosxcosy\mp sinxsiny\)
\(sin2x=2sinxcosx\)
\(cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x\)
\(sin3x=3sinx-4sin^3x\)
\(cos3x=4cos^3x-3cosx\)
\(sinx+siny=2sin\frac{x+y}{2}cos\frac{x-y}{2}\)
\(sinx-siny=2cos\frac{x+y}{2}sin\frac{x-y}{2}\)
\(cosx+cosy=2cos\frac{x+y}{2}cos\frac{x-y}{2}\)
\(cosx-cosy=-2sin\frac{x+y}{2}sin\frac{x-y}{2}\)
\(sinxsiny=\frac{1}{2}[cos(x-y)-cos(x+y)]\)
\(cosxcosy=\frac{1}{2}[cos(x-y)+cos(x+y)]\)
\(sinxcosy=\frac{1}{2}[sin(x+y)+sin(x-y)]\)
\(sin^2x=\frac{1}{2}[1-cos2x]\)
\(cos^2x=\frac{1}{2}[1+cos2x]\)
二项式定理：\((a+b)^n=\sum_{k=0}^n{C_n^ka^{n-k}b^k}\)

夹逼准则和单调有界准则

夹逼准则：如果\(\forall x \in (a,b),f(x)\leq g(x)\leq h(x)\)，且\(lim_{x\to a}{f(x)}=lim_{x\to a}{h(x)}=A\)，则\(lim_{x\to a}{g(x)}=A\)。
单调有界准则：如果\(\{x_n\}\)单调递增且有上界，则\(\{x_n\}\)收敛；如果\(\{x_n\}\)单调递减且有下界，则\(\{x_n\}\)收敛。

无穷小

定义：如果\(\lim_{x\to x_0}{f(x)}=0\)，则称f(x)是当\(x\to x_0\)时的无穷小。

无穷小的运算性质：有界函数与无穷小的乘积是无穷小。

无穷大

定义：如果\(\lim_{x\to x_0}{f(x)}=\infty\)，则称f(x)是当\(x\to x_0\)时的无穷大。

无穷小的比较

等价无穷小：如果\(\lim_{x\to x_0}{\frac{f(x)}{g(x)}}=1\)，则称f(x)与g(x)是当\(x\to x_0\)时的等价无穷小，记为\(f(x)\sim g(x)\)。
同阶无穷小：如果\(\lim_{x\to x_0}{\frac{f(x)}{g(x)}}=A(A\ne 0)\)，则称f(x)与g(x)是当\(x\to x_0\)时的同阶无穷小，记为\(f(x)=O(g(x))\)。
高阶无穷小：如果\(\lim_{x\to x_0}{\frac{f(x)}{g(x)}}=0\)，则称f(x)是当\(x\to x_0\)时的高阶无穷小，记为\(f(x)=o(g(x))\)。
低阶无穷小：如果\(\lim_{x\to x_0}{\frac{f(x)}{g(x)}}=\infty\)，则称f(x)是当\(x\to x_0\)时的低阶无穷小，记为\(f(x)=\omega(g(x))\)。
k阶无穷小：如果\(\lim_{x\to x_0}{\frac{f(x)}{g(x)^k}}=A(A\ne 0)\)，则称f(x)是当\(x\to x_0\)时的k阶无穷小，记为\(f(x)=O(g(x)^k)\)。

等价无穷小的两个定理

为等价无穷小的充分必要条件：如果\(f(x)\sim g(x)\)，则\(f(x)=g(x)+o(g(x))\)。
如果\(\alpha \sim \alpha '\)，\(\beta \sim \beta '\)，且\(\lim_{x\to x_0}{\frac{\alpha}{\beta}}=A(A\ne 0)\)，则\(\lim_{x\to x_0}{\frac{\alpha '}{\beta '}}=A\)。

函数在一点的连续性

定义：如果\(\lim_{x\to x_0}{f(x)}=f(x_0)\)，则称f(x)在\(x_0\)处连续。

函数在区间上的连续性

定义：如果\(\forall x \in (a,b),\lim_{x\to x_0}{f(x)}=f(x_0)\)，则称f(x)在\((a,b)\)上连续。

函数的间断点

第一类间断点：如果\(\lim_{x\to x_0^-}{f(x)}\)和\(\lim_{x\to x_0^+}{f(x)}\)存在，但不相等，则称\(x_0\)是f(x)的第一类间断点。
第二类间断点：如果\(\lim_{x\to x_0^-}{f(x)}\)和\(\lim_{x\to x_0^+}{f(x)}\)至少有一个不存在，则称\(x_0\)是f(x)的第二类间断点。

可去间断点：如果\(\lim_{x\to x_0}{f(x)}\)存在，但与\(f(x_0)\)不相等，则称\(x_0\)是f(x)的可去间断点。

跳跃间断点：如果\(\lim_{x\to x_0^-}{f(x)}\)和\(\lim_{x\to x_0^+}{f(x)}\)存在，且相等，则称\(x_0\)是f(x)的跳跃间断点。

无穷间断点：如果\(\lim_{x\to x_0^-}{f(x)}\)和\(\lim_{x\to x_0^+}{f(x)}\)至少有一个为无穷，则称\(x_0\)是f(x)的无穷间断点。

振荡间断点：如果\(\lim_{x\to x_0^-}{f(x)}\)和\(\lim_{x\to x_0^+}{f(x)}\)不存在，则称\(x_0\)是f(x)的振荡间断点。

其中，可去间断点和跳跃间断点统称为第一类间断点，无穷间断点和振荡间断点统称为第二类间断点。

初等函数的连续性

连续函数的四则运算的结果仍然是连续函数。
反函数的连续性：如果f(x)在\(x_0\)处连续且\(f'(x_0)\ne 0\)，则\(f^{-1}(x)\)在\(y_0=f(x_0)\)处连续。
复合函数的连续性：如果 g(x) 在某个点 a 处连续，并且 f(x) 在 g(a) 处连续，那么复合函数 h(x) = f(g(x)) 在点 a 处连续。换句话说，如果组成复合函数的内部函数 g(x) 在某个点处连续，而外部函数 f(x) 在该内部函数的值处连续，那么复合函数在该点处连续。

闭区间连续函数的性质

有界性：如果f(x)在\([a,b]\)上连续，则f(x)在\([a,b]\)上有界。
最值定理：如果f(x)在\([a,b]\)上连续，则f(x)在\([a,b]\)上有最大值和最小值。
介值定理：如果f(x)在\([a,b]\)上连续，且\(f(a)\ne f(b)\)，则对于\(\forall y \in (f(a),f(b))\)，\(\exists x_0 \in (a,b)\)，使得\(f(x_0)=y\)。