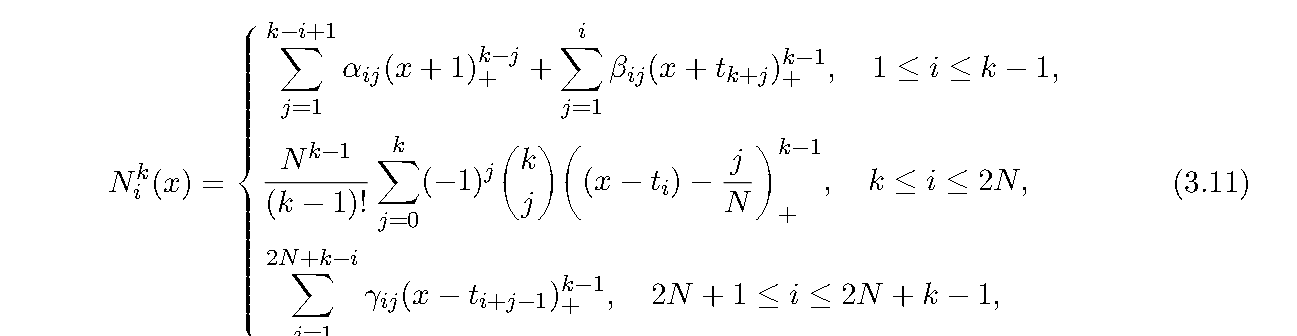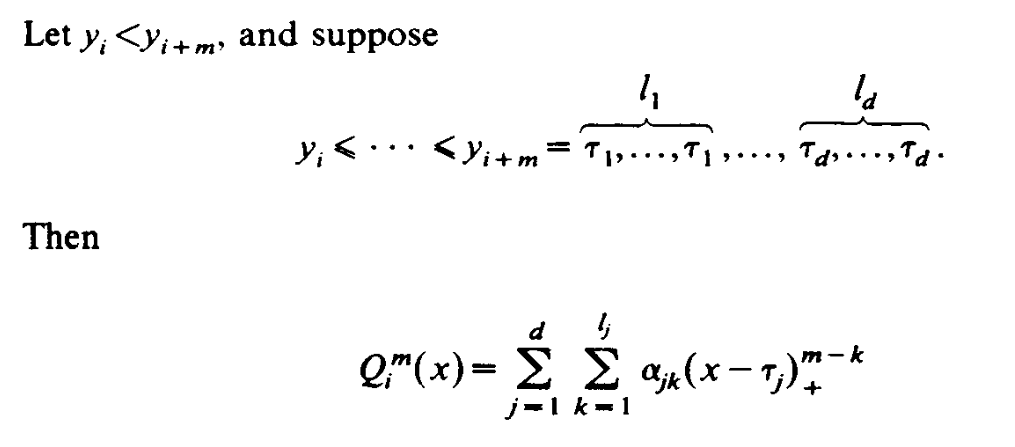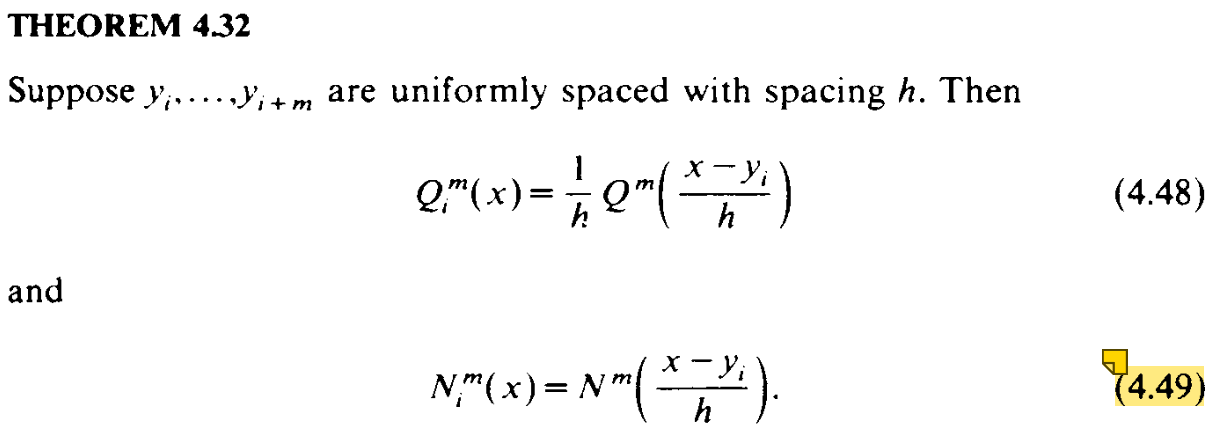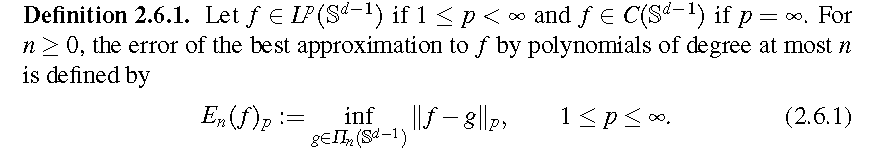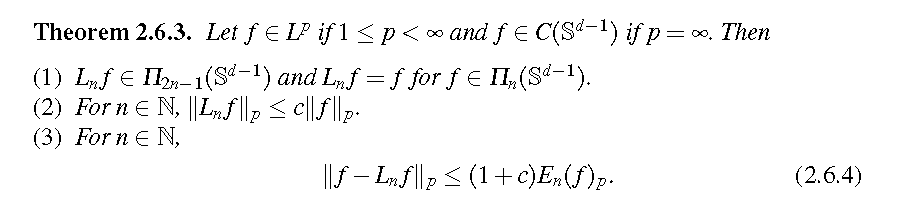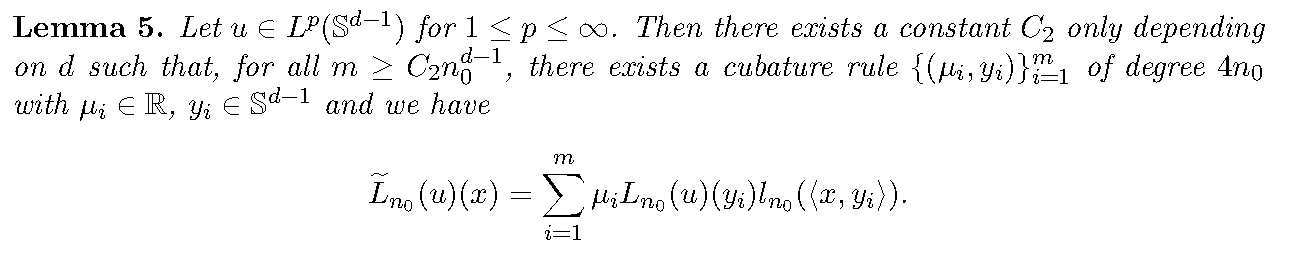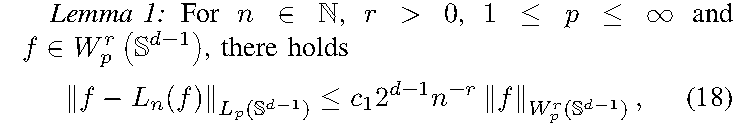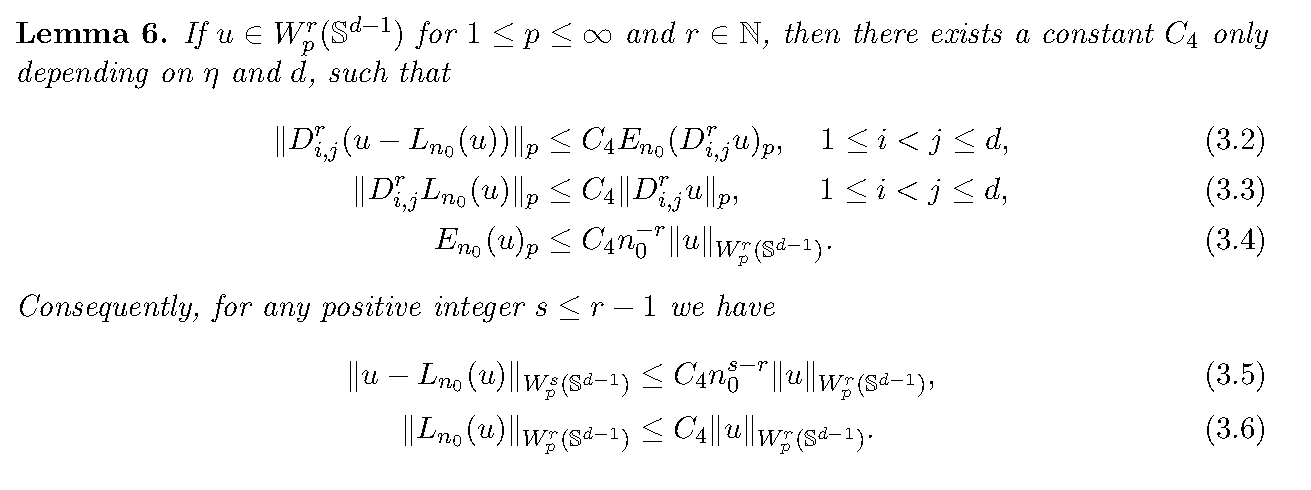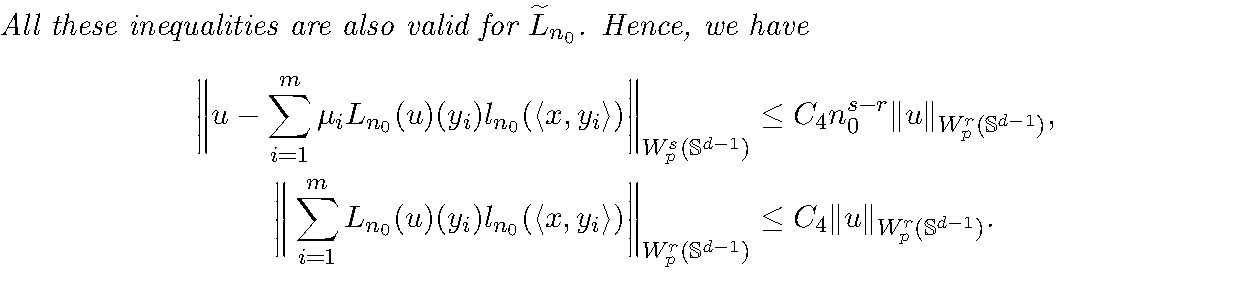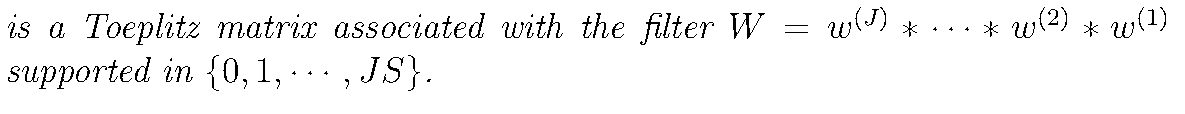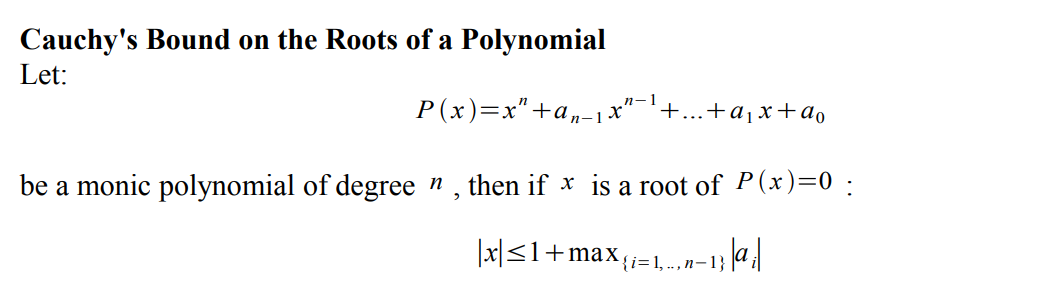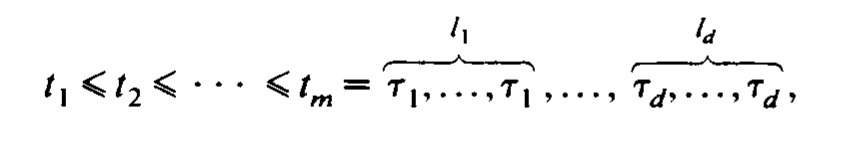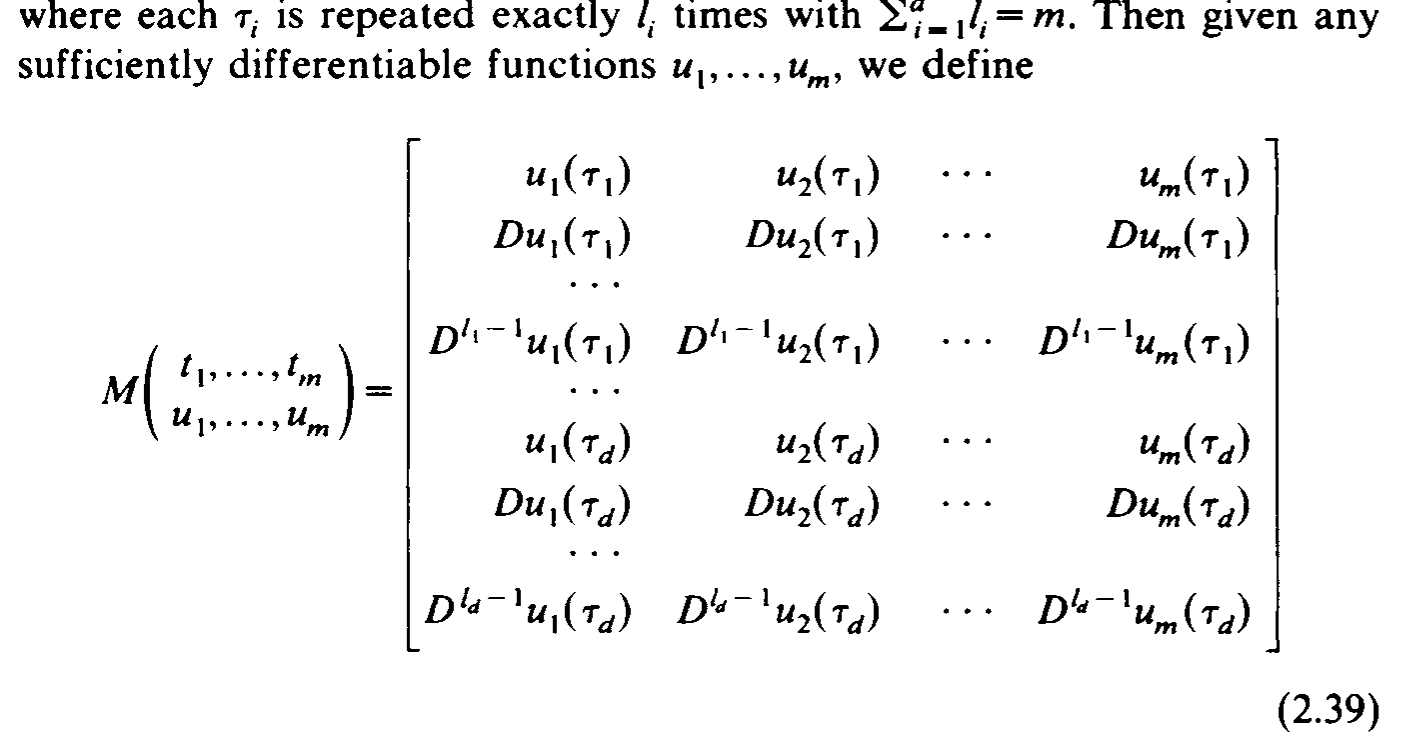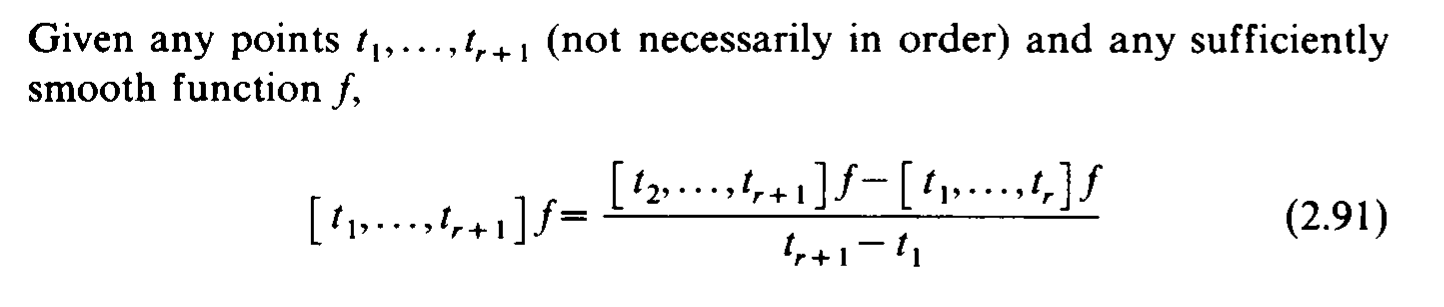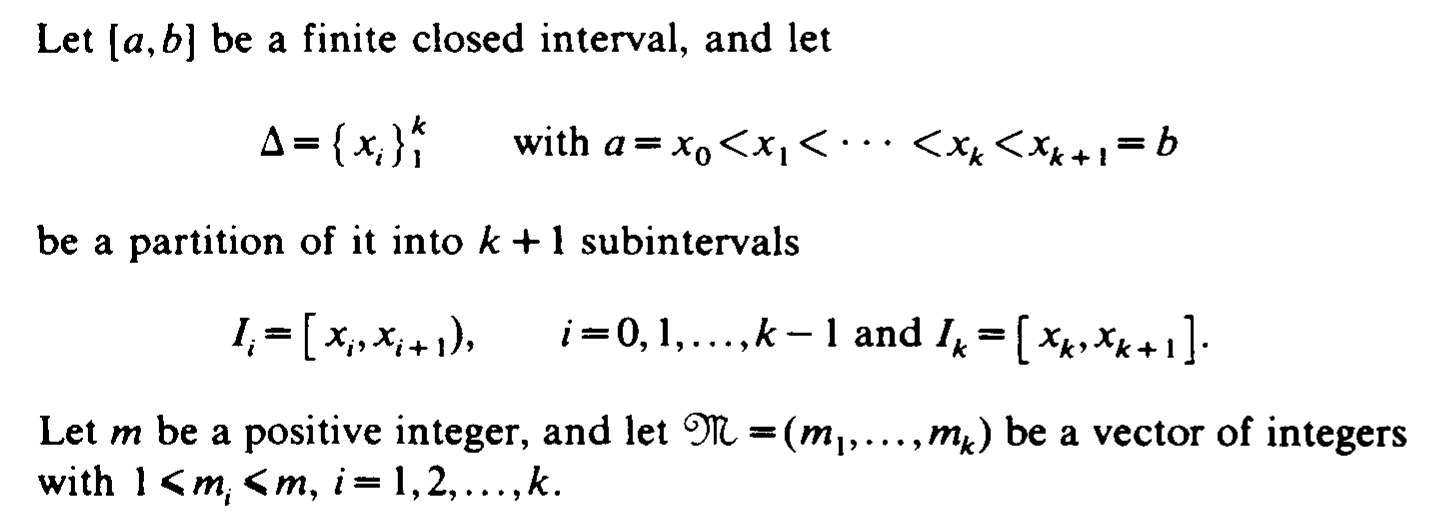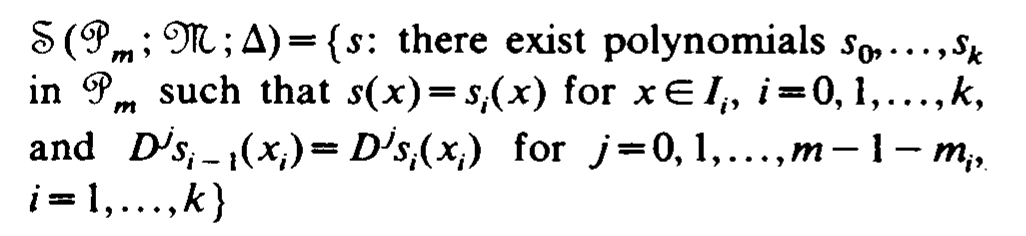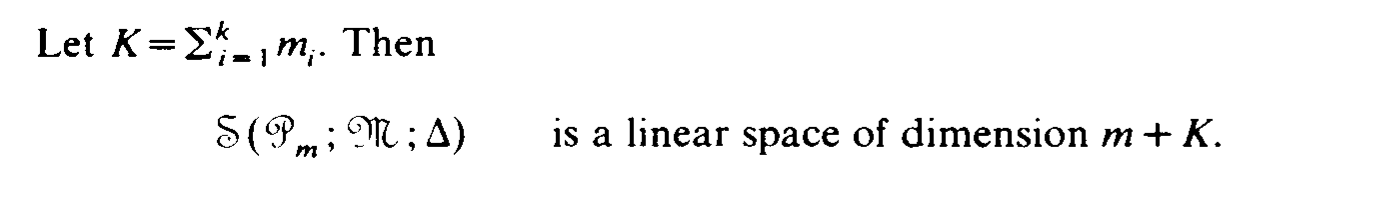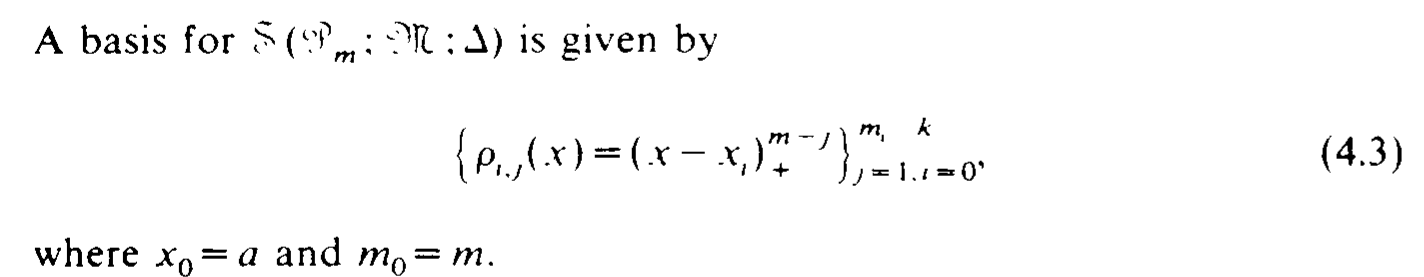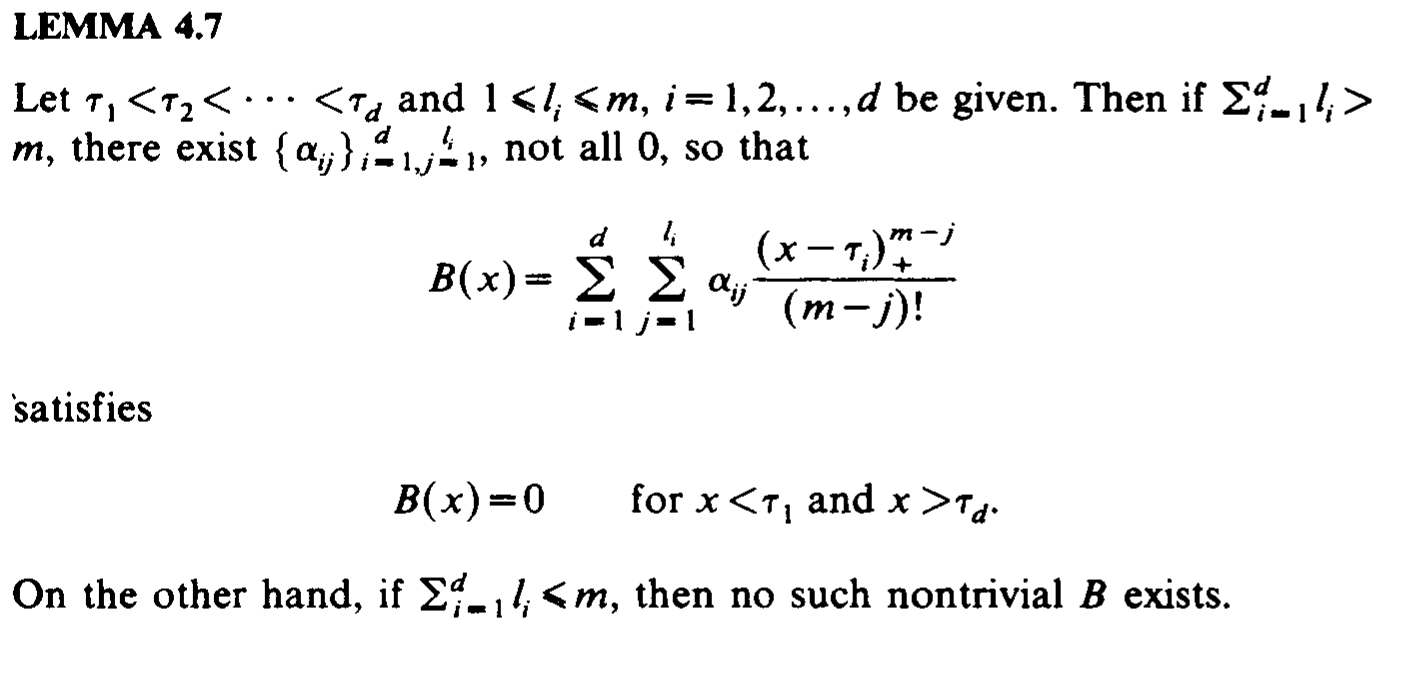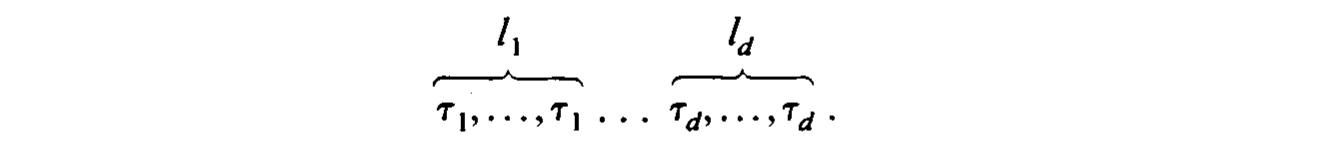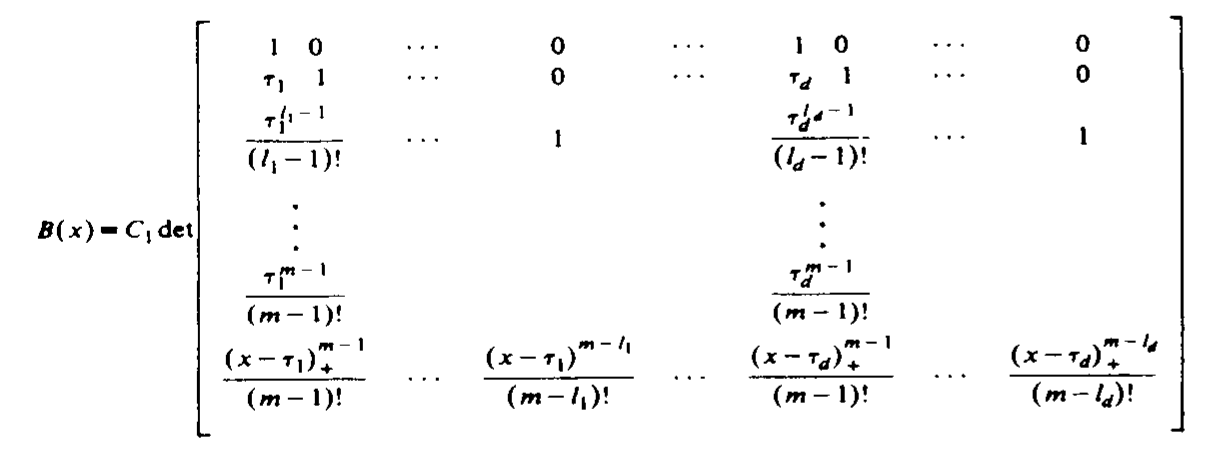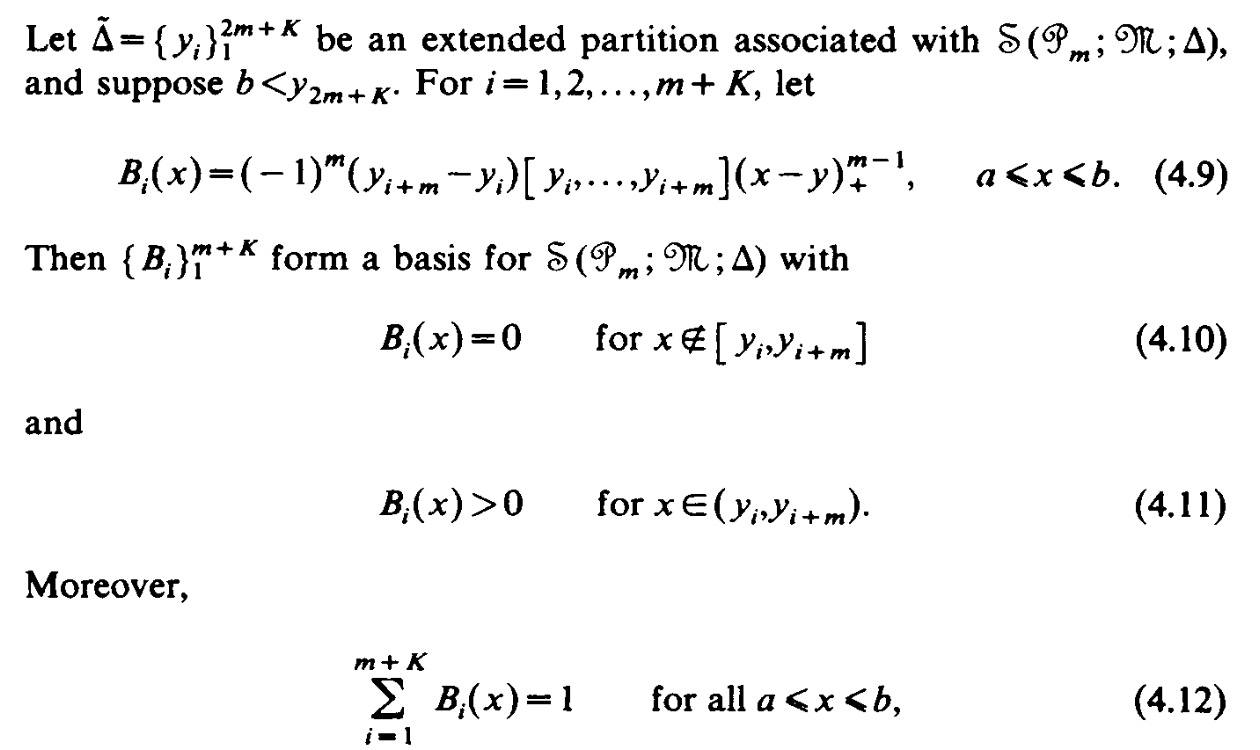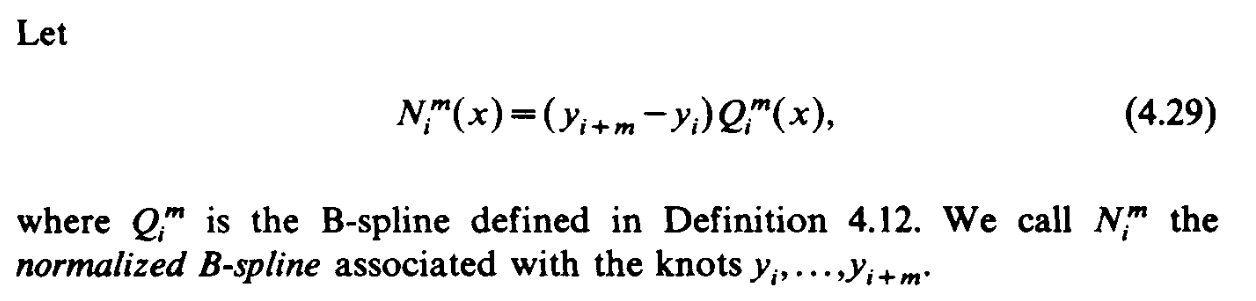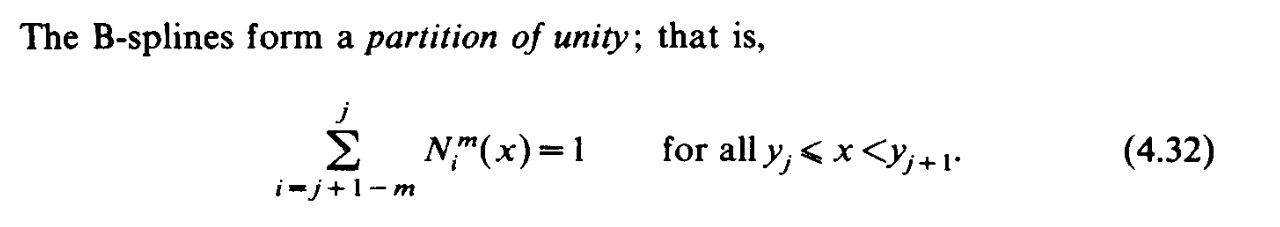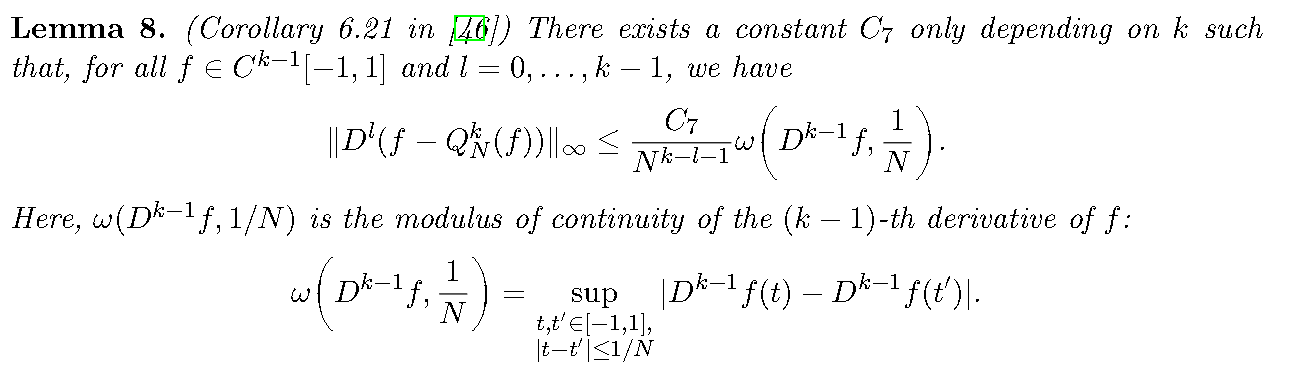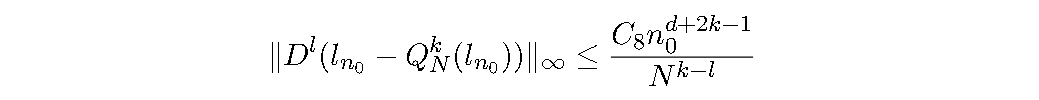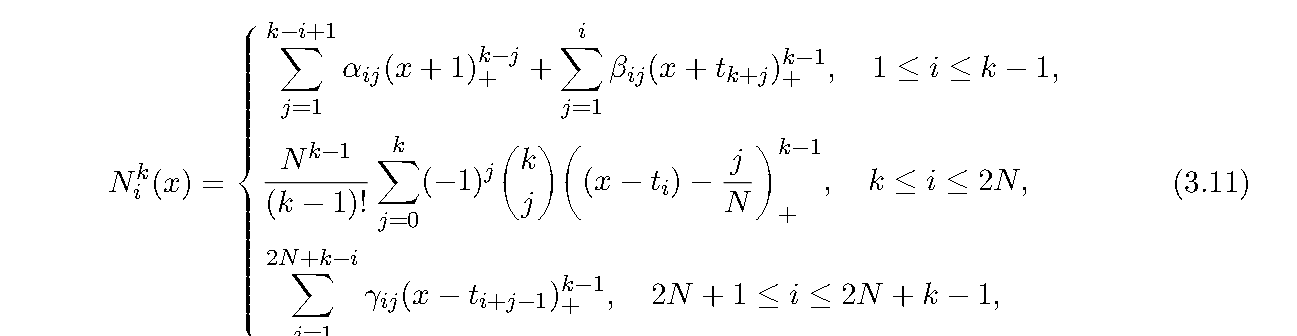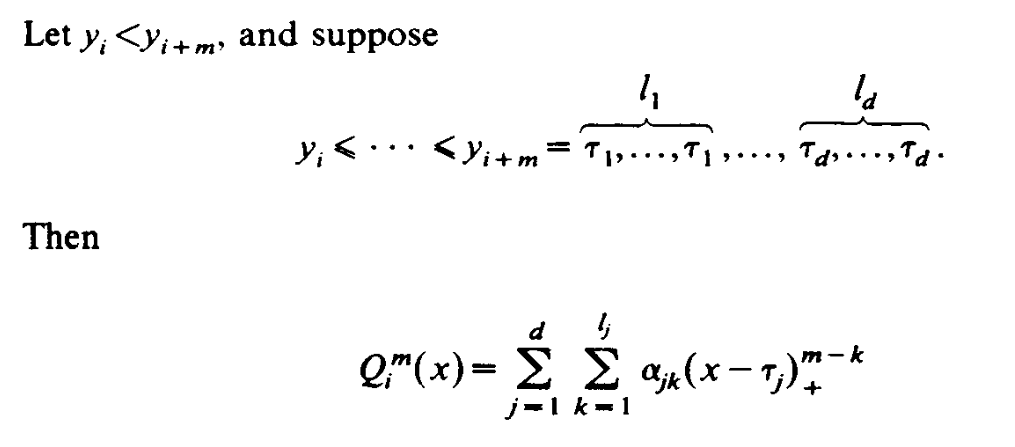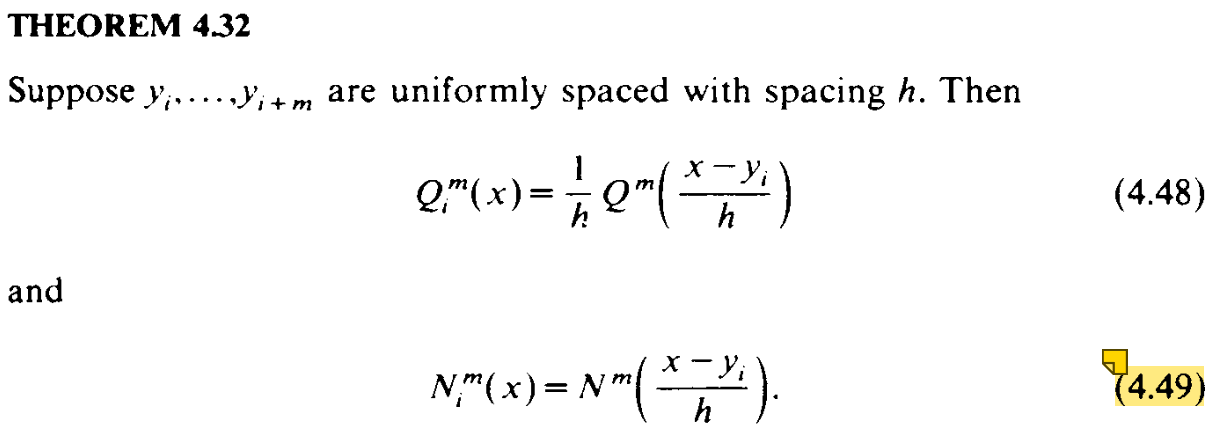# Solving PDEs on Spheres with PICNN report_2
本次报告主要针对逼近误差(approximation error)的分析
1. Near-Best Approximation
1.1. 符号、定义、基本性质

引入两个记号:
- \(\mathscr{P}_{n}^{d}\) 表示 \(n\) 次齐次多项式空间,满足 \(\operatorname{dim}\mathscr{P}_{n}^{d} = \binom{n+d-1}{n}\)
- \(\varPi_{n}^{d}\) 表示次数 \(\le n\) 的多项式空间,满足 \(\operatorname{dim}\varPi_n^d = \binom{n+d}{n}\)
所谓的球谐函数就是调和多项式函数在球面上的限制,确切来说
\[\mathscr{H}_{n}^{d} = \{ P \in \mathscr{P}_{n}^{d}: \triangle P = 0 \}
\]
定义在 \(\mathbb{R}^{d}\)上,我们可以通过下面的操作将其限制在球面 \(\mathbb{S}^{d-1}\)上
\[if \quad Y \in \mathscr{H}_{n}^{d},\quad then\quad Y(x) = ||x||^nY(x') \quad x' \in \mathbb{S}^{d-1}
\]
以后若无额外说明. 我们把 \(\mathscr{H}_{n}^{d}\) 理解为球谐函数空间.
定义内积
\[\left<f,g\right>_{\mathbb{S}^{d-1}} = \frac{1}{\omega_{d}}\int_{\mathbb{S}^{d-1}}f(x)g(x)\mathrm{d}\sigma(x)
\]
一个有用的结论是不同次的球谐函数在此内积的意义下正交(利用分部积分)
定理1
\[\left<\mathscr{H}_{n}^{d},\mathscr{H}_{m}^{d}\right>_{\mathbb{S}^{d-1}} = 0,\quad m \neq n
\]
另外,可以将齐次函数空间分解为球谐函数空间:
定理2
\[\mathscr{P}_{n}^{d} = \mathop{\LARGE{\oplus }}\limits _{0\le j\le \frac{2}{n}} ||x||^{2j}\mathscr{H}^{d}_{n-2j}
\]
这样我们就可以用正交和齐次性质导出球谐性质,确切来说
若\(P\) 为 \(n\) 次齐次函数,且正交于所有次数小于 \(n\) 的多项式 \(\Longrightarrow P \in \mathscr{H}_{n}^{d}\)
还可以导出:
\[\operatorname{dim}\mathscr{H}_{n}^{d} = \operatorname{dim}\mathscr{P}_{n}^{d} - \mathscr{P}_{n-2}^{d} = \binom{n+d-1}{n} - \binom{n+d-3}{n-2}
\]
\[\operatorname{dim} \varPi_{n}(\mathbb{S}^{d-1})= \mathscr{P}_{n}^{d}+\mathscr{P}_{n-1}^{d}= \binom{n+d-1}{n} + \binom{n+d-2}{n-1}
\]
投影算子:\(proj_{n}: L^{2}(\mathbb{S}^{d-1}) \mapsto \mathscr{H}_{n}^{d}\)
一个重要的性质是,\(\mathscr{H}_{n}^{d}\)的再生核与投影算子核有相同的形式:
\(\mathscr{H}_{n}^{d}\)的 reproducing kernel \(Z_n(\cdot ,\cdot )\)由下面的式子决定:
\[\frac{1}{\omega_d} \int_{\mathbb{S}^{d-1}}Z_n(x,y)p(y)\mathrm{d}\sigma(y) = p(x), \forall p \in \mathscr{H}_{n}^{d}, \quad x \in \mathbb{S}^{d-1}
\]
良定义且唯一(Riesz 表示定理作用于赋值泛函)
\[proj_nf(x) = \int_{\mathbb{S}^{d-1}}Z_n(x,y)f(y)\mathrm{d}\sigma(y)
\]
可以通过变量替换证明 \(Z_n(x,y)\) 只依赖于 \(\left<x,y\right>\),引出 zonal harmonic,进一步的,我们可以导出再生核的闭形式:
\[Z_n(x,y) = \frac{n+\lambda}{\lambda} C_{n}^{\lambda}(\left<x,y\right>)
\]

定义卷积
\[(f*g)(x) = \frac{1}{\omega_d}\int_{\mathbb{S}^{d-1}}f(y)g(\left<x,y\right>)\mathrm{d}\sigma(y)
\]
其中 \(f \in L^{1}(\mathbb{S}^{d-1})\),\(g \in L^{1}(w_\lambda;[-1,1])\),\(\lambda = \frac{d-2}{2}\)
\[||g||_{\lambda,p} =\displaystyle \left(c_\lambda \int_{-1}^{1} |g(x)|^{p}w_\lambda(x) \mathrm{d}x\right) ^{\frac{1}{p}},\quad 1\leq p \leq \infty, \quad w_\lambda(x) = (1-x^2)^{\lambda - \frac{1}{2}},\quad \lambda > -\frac{1}{2}, \quad x \in (-1,1).
\]
对于 $ f\in L{2}(\mathbb{S})$做傅里叶展开,我们可以将 \(L^{2}(\mathbb{S}^{d-1})\)分解为球谐空间的直和形式. (多项式逼近连续函数,连续函数逼近 \(L^2\) 函数)
\[L^2(\mathbb{S}^{d-1}) = \sum_{n=0}^{\infty}\mathscr{H}_{n}^{d} \quad i.e. \quad f = \sum_{n=2}^{\infty} proj_n f
\]
在 $\lim_{n \to \infty} ||f-S_nf||_2 = 0 $的意义下,同时成立 Parseval's 等式
在结合之前投影算子的公式(再生核)我们有以下定理
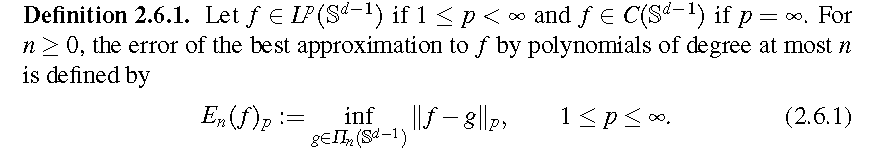
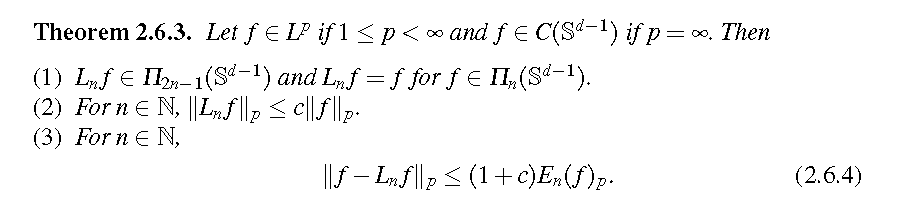
\[L_nf = \sum_{k=0}^{\infty}\eta(\frac{k}{n}) proj_nf
\]
\[||f-L_nf||_{p} \leq ||f-p_n||+||L_n(f-p_n)|| \leq (1+c)||f-p_n||_p = (1+c)E_n(f)_p
\]
接下来要做的就是把 \(L_nf\) 离散化.
1.2. 离散化
引理 存在一个只依赖于 \(d\) 的正常数 \(c\) 使得对任意 \(m\),当 \(m \geq cn^{d-1}\) 时,存在正数 \(\lambda_j\) 和 点 \(z_j \in \mathbb{S}^{d-1}, j=1, \ldots ,m.\) 满足
\[\int_{\mathbb{S}^{d-1}} f(x)\mathrm{d}\mu(x) = \sum_{j=1}^{m}\lambda_j f(z_j), \quad \forall f \in \varPi_{4n}(\mathbb{S}^{d-1})
\]
进一步,对于 \(f \in \varPi_{4n}(\mathbb{S}^{d-1})\),
\[||f||_p \asymp
\begin{cases}
\left( \sum_{j=1}^{m} \lambda_j|f(z_j)|^{p} \right)^{\frac{1}{p}} , & if \quad 1\leq p < \infty \\
\max_{j=1, \ldots ,m} n^{d-1}\lambda_j|f(z_j)|, &if \quad p = \infty
\end{cases}
\]
特别的,我们称 \(\{ (\lambda_j,z_j) \}_{j=1}^{m}\) 满足次数为 \(4n\) 的容积公式(cubature formula)
应用到本文就得到:
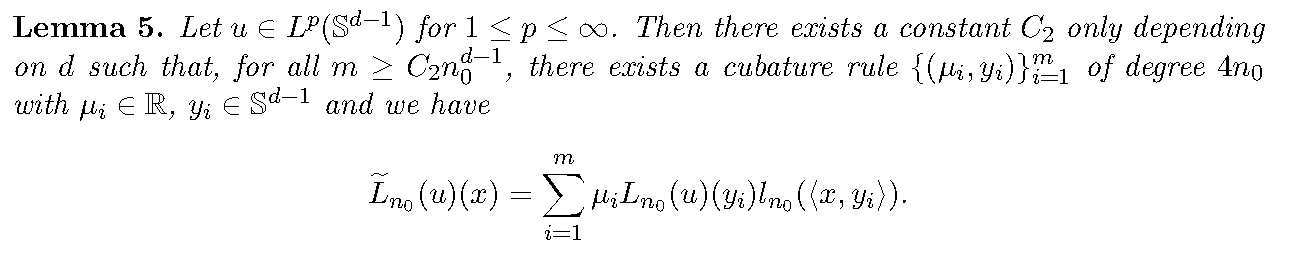
这里需要用到再生核的性质以及不同次的球谐空间正交,这里直接用归一化测度 \(\int_{\mathbb{S}^{d-1}} \mathrm{d}\mu = 1\)
\[\begin{aligned}
\tilde{l}_{n_0}(\left<x,y\right>) &= \sum_{k=0}^{2n_0} \eta(\frac{k}{n_0})\frac{\lambda + k}{\lambda} \int_{\mathbb{S}^{d-1}} C_{k} ^{\lambda} (\left<x,z\right>) \cdot \sum_{l=0}^{2n_0}\eta(\frac{l}{n_0})\frac{\lambda+l}{\lambda}C_{l} ^{\lambda}(\left<z,y\right>) \mathrm{d}\mu(z) \\
&= \int_{\mathbb{S}^{d-1}}l_{n_0}(\left<x,z\right>)l_{n_0}(\left<z,y\right>) \mathrm{d}\mu(z)
\end{aligned}
\]
取 \(cn^{d-1}<m=[c+1]n^{d-1}\leq (c+1)n^{d-1}\) 存在 cubature rule \(\{ (\mu_i,y_i) \}_{i=1}^{m}\) 次数 \(4n\) 使得
\[\int_{\mathbb{S}^{d-1}}l_{n_0}(\left<x,z\right>)l_{n_0}(\left<z,y\right>) \mathrm{d}\mu(z) = \sum_{i=1}^{m}\mu_i l_{n_0}(\left<x,y_i\right>)l_{n_0}(\left<y_i,y\right>)
\]
结合之前的就有
\[\begin{aligned}
\tilde{L}_{n_0}(u)(x) &= \int_{\mathbb{S}^{d-1}}u(y)\sum_{i=1}^{m}\mu_j l_{n_0}(\left<x,y_i\right>)l_{n_0}(\left<y_i,y\right>)\mathrm{d}\mu(y)\\
&= \sum_{i=1}^{m} \mu_i L_{n_{0}}(u)(y_i)l_{n_{0}}(\left<x,y_i\right>)
\end{aligned}
\]
该线性积分算子是有界的,并且提供了Sobolev范数的良好逼近.
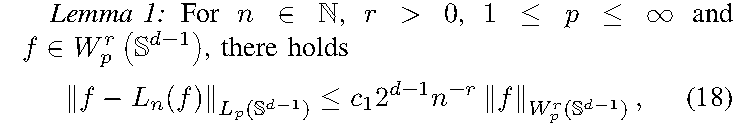
此时我们就有
\[||u-\sum_{i=1}^{m} \mu_i L_{n_{0}}(u)(y_i)l_{n_{0}}(\left<x,y_i\right>)||_p \leq C_{3} n_{0} ^{-r}||u||_{W_{p}^r(\mathbb{S}^{d-1})}
\]
类似还有如下的估计.
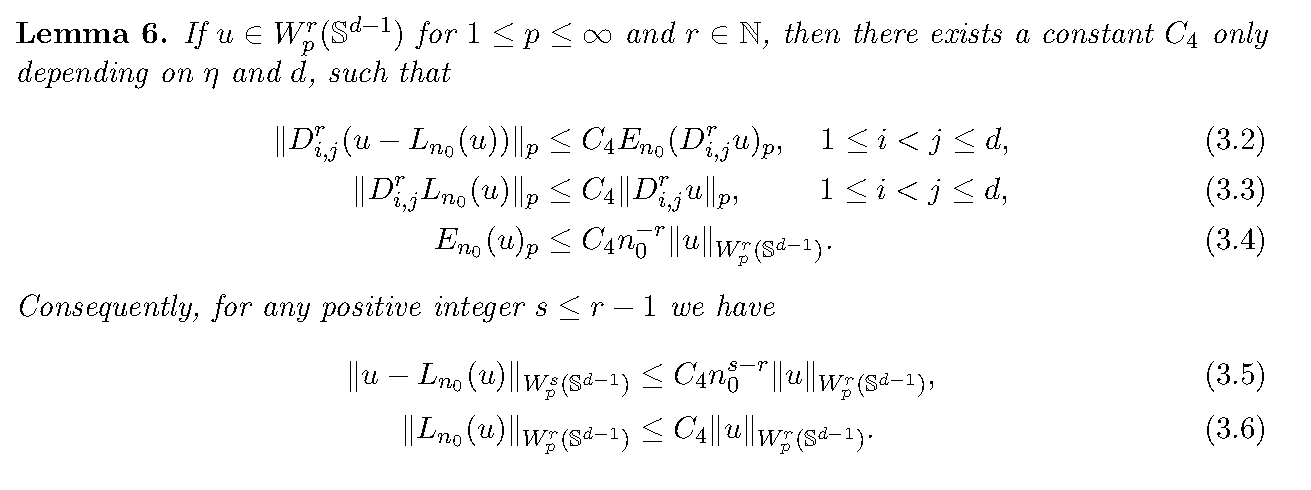
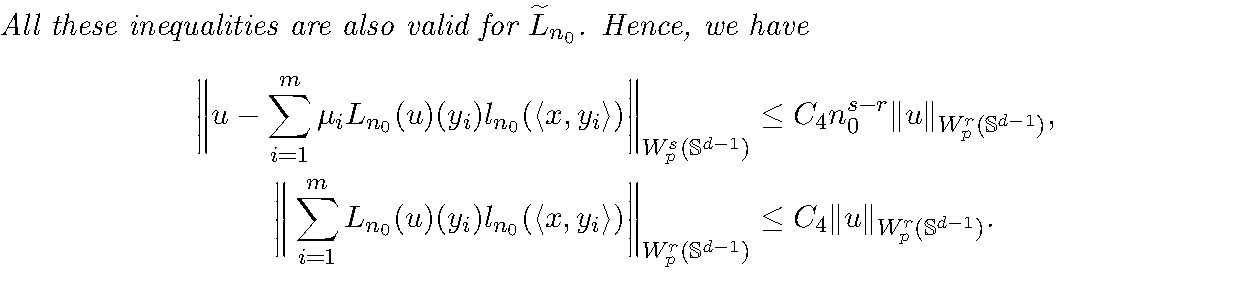
(3.2) 和 (3.4) 是下面这本书中的结论
Feng Dai and Yuan Xu. Approximation Theory and Harmonic Analysis on Spheres and Balls. Springer New York, New York, NY, 2013.
(3.3)(3.5)(3.6)都可以由上面的结论推出:
\[||u-L_{n_0}(u)||_{W_{[p]}^{s}(\mathbb{S}^{d-1})} = ||u-L_{n_0}(u)||_{p}+\sum_{1\leq i < j \leq d} ||D_{i,j}^{s}(u-L_{n_0}(u))||_{p}
\]
\[||u-L_{n_0}(u)||_{p} \leq C_4E_{n_0}(u)_{p}\leq C_4n_0^{-r}||u||_{W_{p}^{r}(\mathbb{S}^{d-1})}
\]
\[||D_{i,j}^{s}(u-L_{n_0}(u))||_{p} \leq C_4E_{n_0}(D_{i,j}^{s}u)_{p}\leq C_4n_0^{s-r}||u||_{W_{p}^{r}(\mathbb{S}^{d-1})}
\]
2. 提取特征
给定 cubature rule \(\{ (\mu_i, y_i) \}_{i=1}^{m}\),通过采样层,卷积层就可以提取内积 \(\left<x,y_i\right> \text{for } i = 1,2, \ldots ,m\) 作为特征. 也即下面的引理:


首先证明下面两个引理:

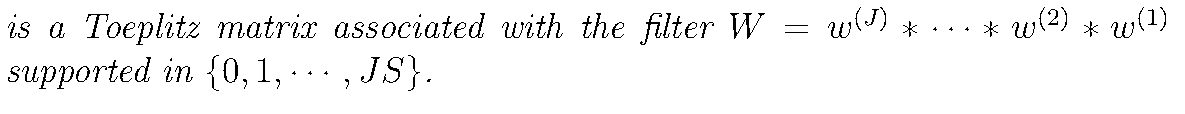
第一个引理的证明是利用了多项式相乘与卷积运算的一致性:
定义 \(\mathbb{C}\) 上的多项式 \(\tilde{w}(z) = \sum_{k=0}^{\infty}w_kz^{k}\) 卷积运算:\(\widetilde{a*b} = \tilde{a}(z)\tilde{b}(z)\). 注意到 \(\tilde{W}\) 是次数为 \(M \in [0,\mathcal{M}]\) 的实系数多项式,故其复根成对出现且可以分解为
\[\tilde{W}(z) = W_{M} \prod_{k=1}^{K}\{ z^{2}-2x_kz + (x_k^{2}+y_k^{2}) \} \prod_{k=2K+1}^{M} (z-x_k)
\]
适当的组合右边的多项式使他们的次数都小于 S,我们就可以得到分解
\[\tilde{W}(z) = \widetilde{w^{(J)}} \cdots\widetilde{w^{(2)}}\widetilde{w^{(1)}}
\]
此即分解:
\[W = w^{(J)}*w^{(J-1)}*\cdots*w^{(2)}*w^{(1)}
\]
第二个引理:首先有卷积公式:
\[(a*b)_i = \sum_{k \in \mathbb{Z}} a_{i-k}b_k, \quad i \in \mathbb{Z}
\]
如果 \(a\) 的支撑集在 \(\{ A_0,A_0+1, \ldots ,A_1 \}\) 且 \(b\) 的支撑集在 \(\{ B_0,B_0+1, \ldots ,B_1 \}\),则卷积的支撑集在 \(\{ A_0+B_0,A_0+B_0+1, \ldots ,A_1+B_1 \}\),现在考虑 \(d_j \times d_{j-2}\) 矩阵 \(T^{w^{(j)}}_{d_{j-1}}T^{w^{(j-1)}}_{d_{j-2}}\) 有
\[(T^{w^{(j)}}_{d_{j-1}}T^{w^{(j-1)}}_{d_{j-2}})_{i,k} = \sum_{l=1}^{d_{j-1}}w_{i-l}^{(j)}w_{l-k}^{(j-1)}
\]
若 $l \leq 0 $,则 $l-k <0 $,故 \(w_{l-k}^{(j-1)} = 0\),对 \(l \geq d_{j-1} +1\),我们有 \(l-k>s\),同样的有 \(w_{l-k}^{(j-1)} = 0\),故
\[(T^{w^{(j)}}_{d_{j-1}}T^{w^{(j-1)}}_{d_{j-2}})_{i,k} = \sum_{l=1}^{d_{j-1}}w_{i-l}^{(j)}w_{l-k}^{(j-1)} = \sum_{p \in \mathbb{Z}} w^{(j)}_{i-k-p}w_{p}^{(j-1)} = (w^{(j)}*w^{(j-1)})_{i-k}
\]
注意这里的卷积核的支撑集变为了 \(2s\)
进行下去就是
\[T^{(j)}\cdots T^{(2)}T^{(1)} = T^{(J,1)} := (W_{i-k})_{i=1, \ldots d+JS,k=1, \ldots ,d} \in \mathbb{R}^{(d+JS)\times d}
\]
是Toeplitz矩阵,卷积核为 \(W = w^{(J)}*\cdots*w^{(2)}*w^{(1)}\),支撑集落在 \(\{ 0,1, \ldots ,JS \}\)
现在我们可以着手证明引理7
对于 \(m \in \mathbb{N}\) 和 \(y = \{ y_1, \ldots ,y_m \} \subset \mathbb{S}^{d-1}\),取 \(W\) 为支撑集 \(\{ 0, \ldots ,md-1 \}\),序列 \(W_{(j-1)d+(d-i)} = (y_j)_i\),这里 \(j \in \{ 1, \ldots ,m \}\),\(i \in \{ 1, \ldots ,d \}\). 由之前的引理,令 \(\mathcal{M} = md-1\),存在卷积核序列使得
\[W = w^{(J)}*w^{(J-1)}*\cdots*w^{(2)}*w^{(1)}
\]
这里 \(J \geq [\frac{\mathcal{M}}{S-1}]\),对于\(j = p+1, \ldots ,J\),我们令 \(w^{(j)}\) 为 delta序列(卷积运算的单位元). 再由引理我们得到
\[T^{(j)}\cdots T^{(2)}T^{(1)} = T^{(J,1)} := (W_{i-k})_{i=1, \ldots d+JS,k=1, \ldots ,d} \in \mathbb{R}^{(d+JS)\times d}
\]
接下来构造bias向量,记 \(||w||_1 = \sum_{k=-\infty}^{\infty}|w_k|\),令 \(b^{(1)} = -||w^{(1)}||_1 1_{d_0}\) 对于 $j=2, \ldots , J $
\[b^{(j)} = (\prod_{p=1}^{j-1}||w^{(p)}||_1 )T^{(j)}1_{d_{j-1}} -(\prod_{p=1}^{j}||w^{(p)}||_1 )1_{d_{j-1}+S}
\]
注意到 \(b_{S+1}^{(j)} = \cdots = b_{d_j-S}^{(j)}\),且 对于 \(x \in \mathbb{S}^{d-1}\) 有 \(||x||_{\infty} \leq 1\). 记 \(||h||_{\infty} = \max \{ ||h_j||_{\infty}:j =1, \ldots ,q \}\) 对向量值函数 \(h:\mathbb{S}^{d-1} \to \mathbb{R}^{q}\),我们有
\[||T^{(j)}h||_{\infty} \leq ||w^{(j)}||_1||h||_{\infty}
\]
因此有
\[(h^{(J)}(x))_{kd} = \left<y_k,x\right> + B^{(J)},\quad k =1, \ldots ,m,
\]
这里 $B^{(J)} = \prod_{p=1}{J}||w||_1 $,利用采样算子得到
\[\mathcal{D}(h^{(J)}(x)) = \begin{bmatrix} \left<y_1,x\right> \\\vdots\\ \left<y_m,x\right>\\0\\\vdots\\0 \\\end{bmatrix}+B^{(J)}1_{[(d+JS)/d]}
\]
自由参数:卷积核序列以及bias向量提供了 \(JS + J(2S - 1) = 3JS-J\)个自由参数
接下来我们证明范数界估计:
通过旋转cubature rule,我们可以假设 \(y_m=(1,0, \ldots ,0)\),也就是说 \(W_{md-1} = 1\),由之前的分解我们有:
\[W(z) = \prod_{i=1}^{s_1}(z^{2}-2x_iz+x_i^2+y_i^2)\prod_{j=2s_1+1}^{md-1} (z-x_j)
\]
根据下面的多项式根的柯西界估计我们有
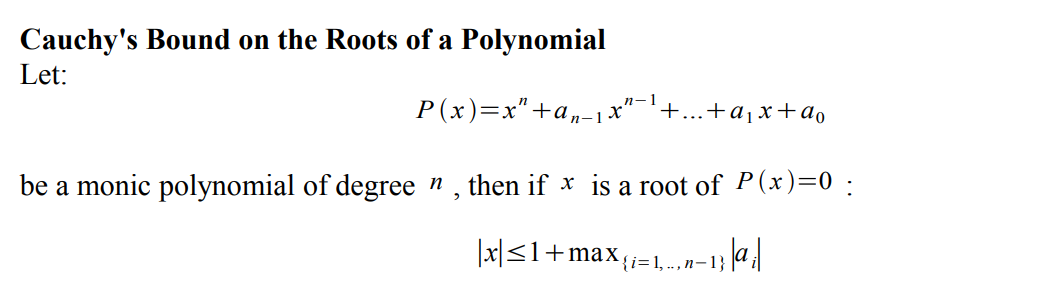
\[|x_j|\vee |x_i\pm iy_i| \leq 1 + \max \{ |\frac{W_{md-2}}{W_{md-1}}|, \ldots ,|\frac{W_0}{W_{md-1}}| \} \leq 2
\]
第二个不等号是因为落在球面上.
所以 \(w^{(l)}(z)\) 的系数被一个只依赖于 \(S\) 的常数 \(C_5\) 控制,即
\[||w^{(l)}||_{\infty} \leq C_5, \quad l=1, \ldots ,L.
\]
考虑到:
\[b^{(j)} = (\prod_{p=1}^{j-1}||w^{(p)}||_1 )T^{(j)}1_{d_{j-1}} -(\prod_{p=1}^{j}||w^{(p)}||_1 )1_{d_{j-1}+S}
\]
我们有
\[||b^{(l)}||_{\infty} \leq (\prod_{i=1}^{l-1}||w^{(i)}||_{1} )\cdot ||w^{(l)}||_1 + \prod_{i=1}^{l} ||w^{(i)}||_{1} \leq 2(\prod_{i=1}^{l} ||w^{(i)}||_{1} ) \leq 2S^{l}C^{l}_{5}
\]
3. B-样条函数逼近
首先引入几个概念:
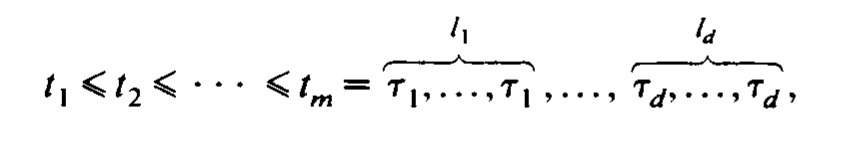
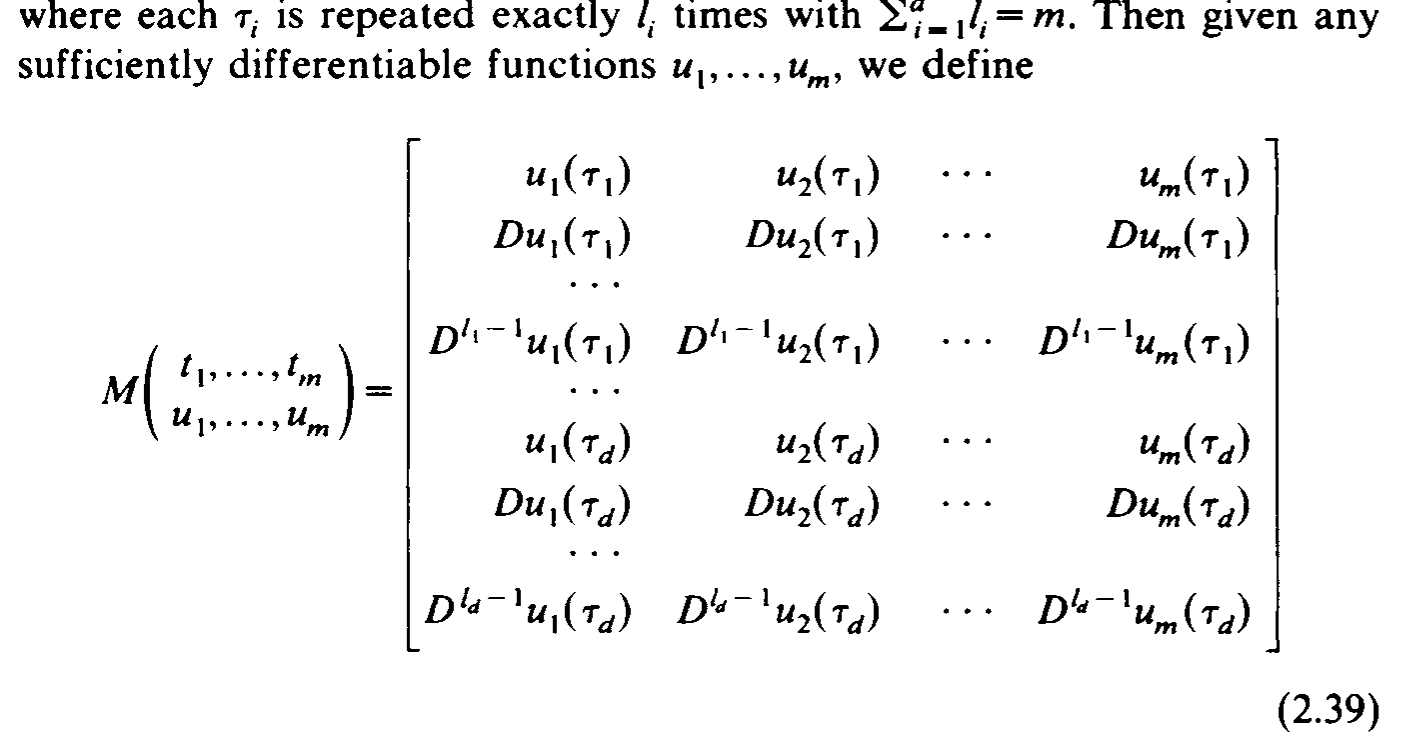
应用
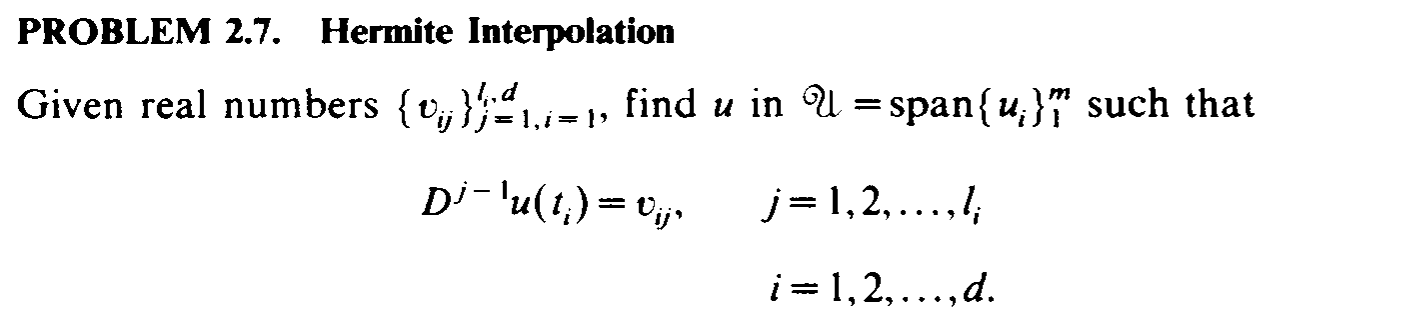
DIVIDED DIFFERENCES

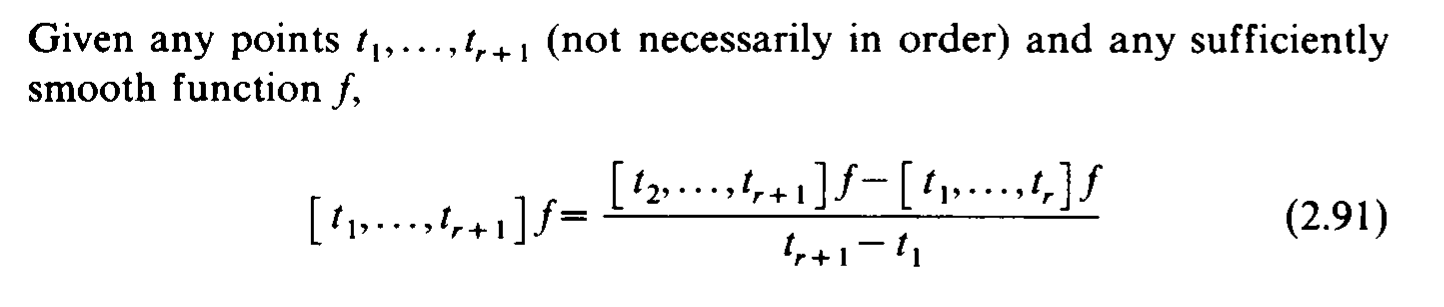
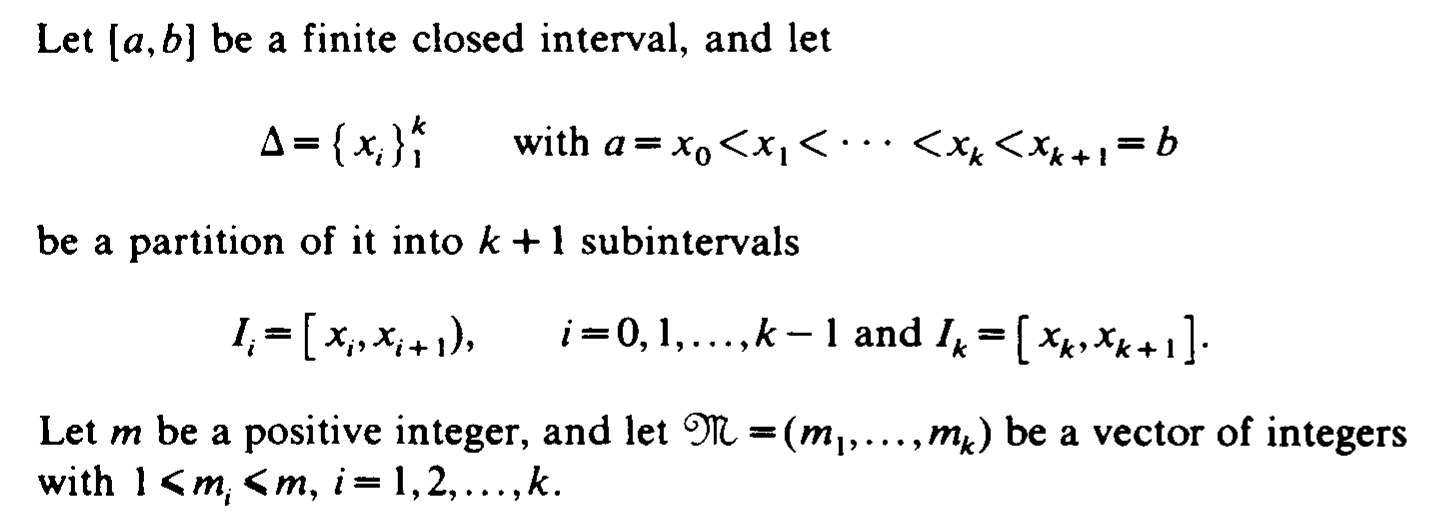
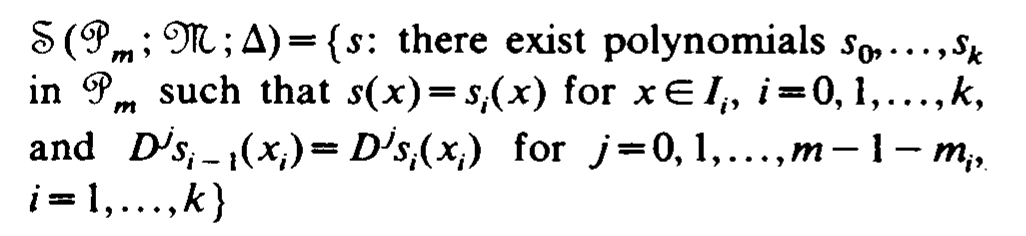
空间的性质
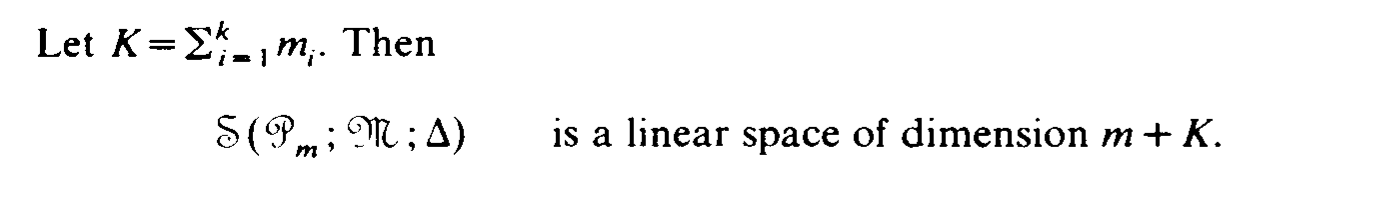
one-sided basis
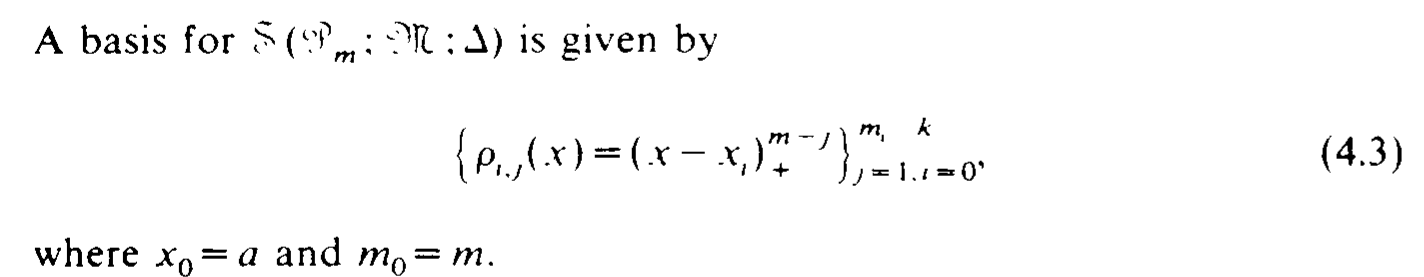
因为 one-sided basis 不方便使用,我们构造了下面一组基:
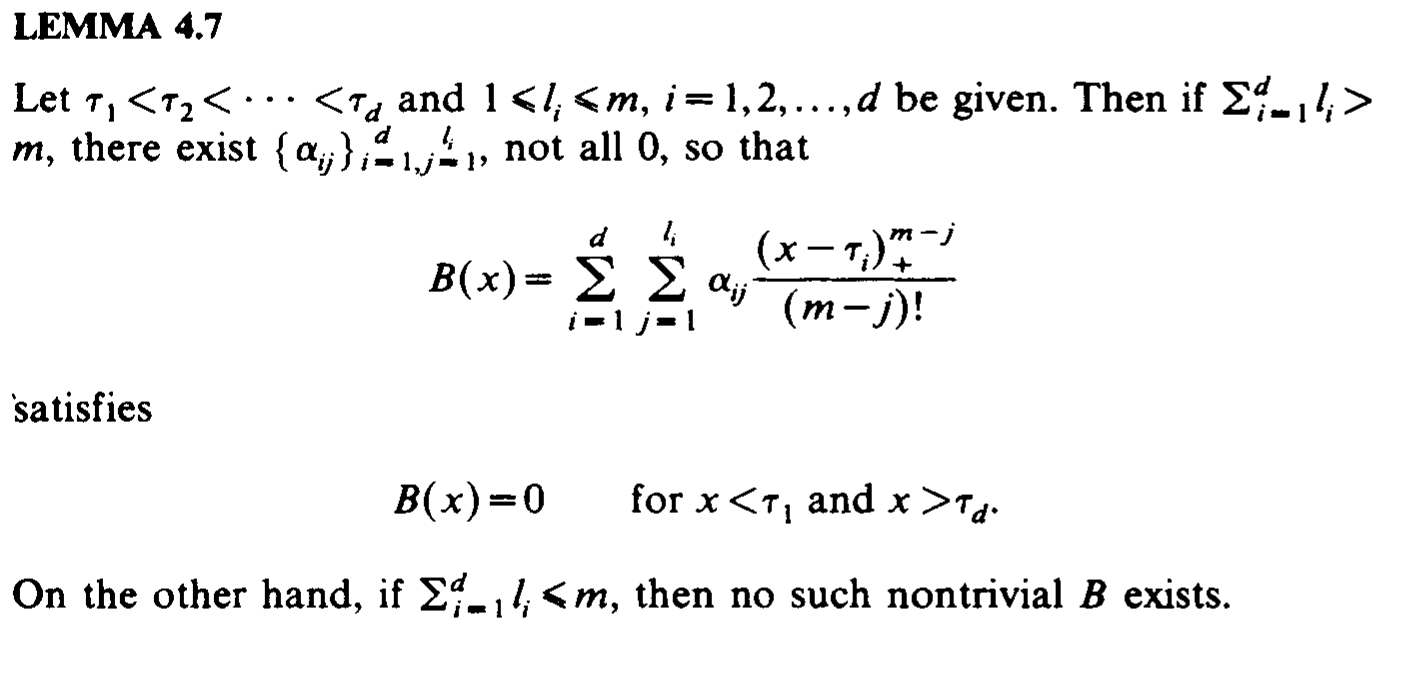
构造过程中发现当 \(\sum_{i=1}^{d} l_i = m + 1\) 时,\(B(x)\) 刚好有 函数 \((x-y)_{+}^{m-1}\) 的 \(m+1\) 阶 divided difference 形式,取点如下.
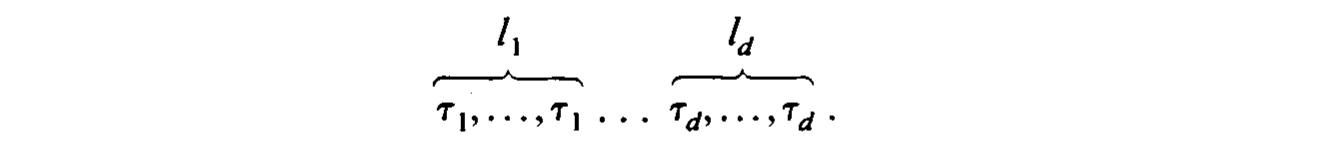
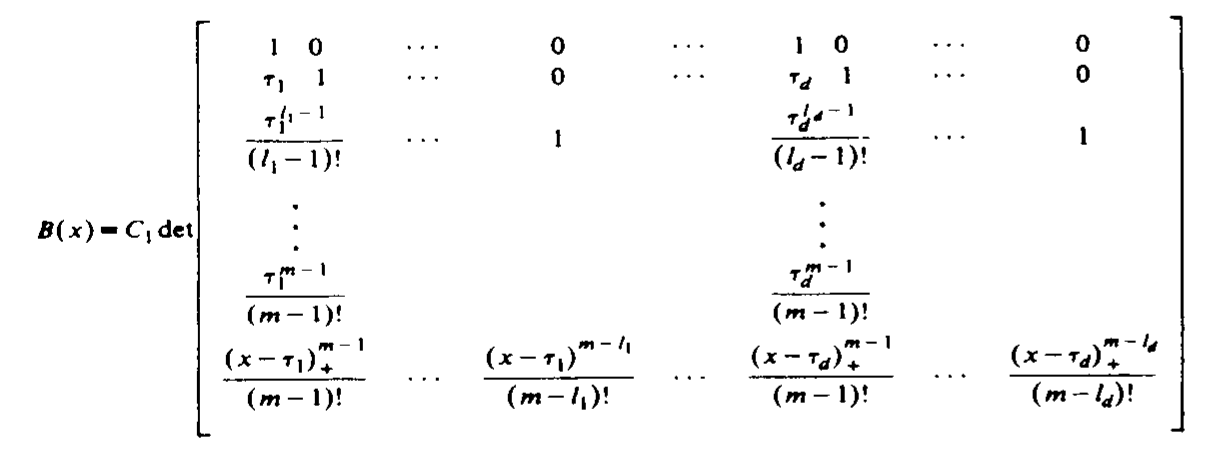
Extended Partition

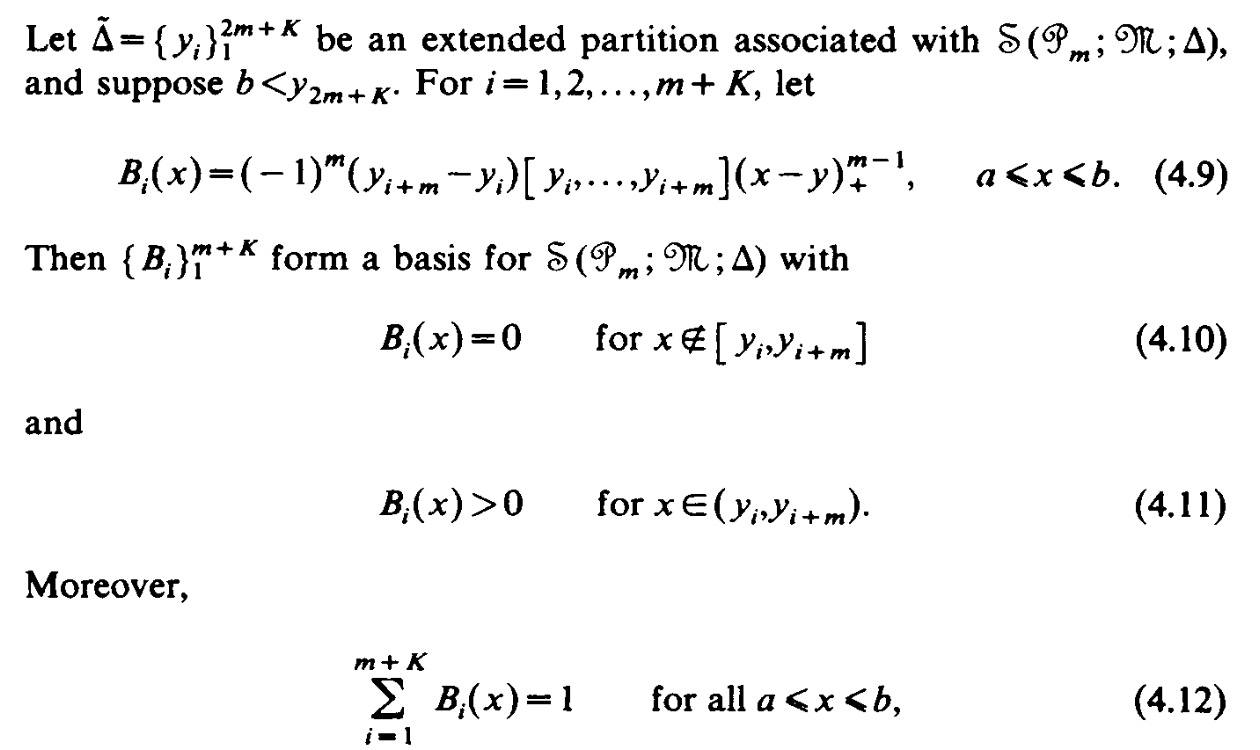
B-Splines

Normalized B-Spllnes
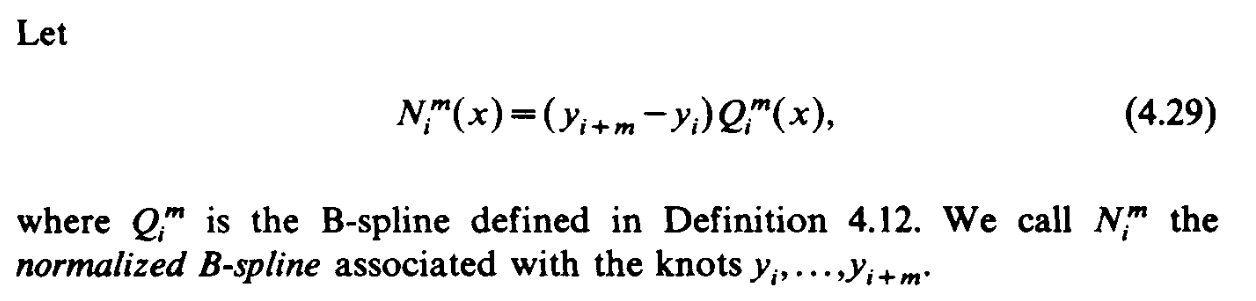
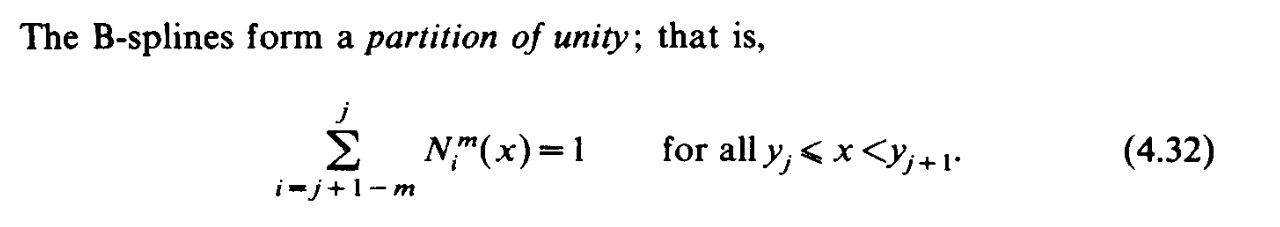
有了这些就可以构造样条插值:
固定 Extended Partition:对于 $ N>0 $
\[t_1 = \cdots = t_k = -1 <t_{k+1} <\cdots < t_{2N+k-1} < 1 = t_{2N+k} = \cdots = t_{2N+2k-1}
\]
其中 \(t_{k+i} = -1 + \frac{i}{N}\) 对 \(i = 0, \ldots ,2N\),对 \(f \in C[-1,1]\),有如下插值
\[Q_{N}^{k}(f) = \sum_{i=1}^{2N+k-1}J_i(f)N_i^{k}(x)
\]
有如下估计
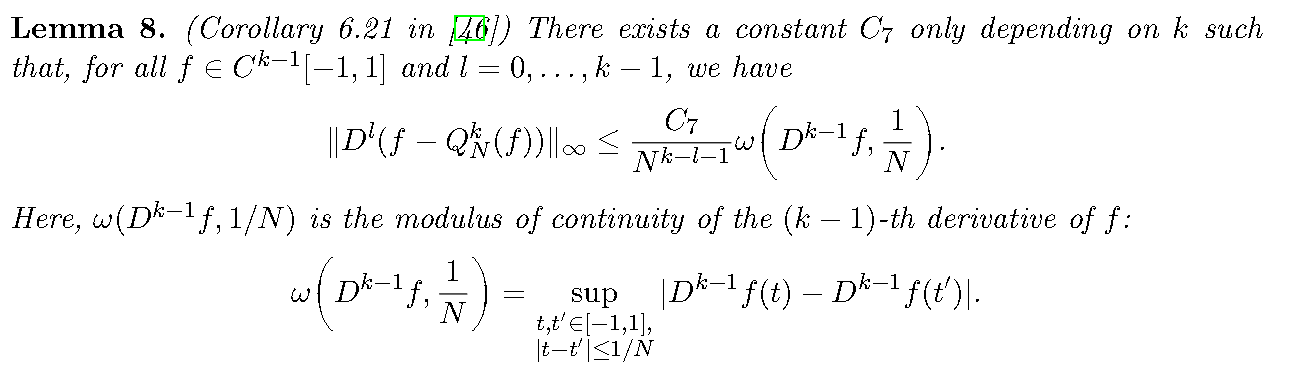
具体的 \(l_{n_0}\in C^{\infty}[-1,1]\),有 $||C_k^{\lambda}||_{\infty} = C_k^{\lambda}(1) = \tbinom{k+d-3}{k} \leq (k+1)^{d-3} $ 有如下估计
\[||l_{n_0}||_{\infty} \leq 5 \cdot 3^{d-2}n_0^{d-1}
\]
由于 \(l_{n_0}\) 为次数至多为 \(2n_0\) 的多项式,由 Markov不等式
\(P(x)\) 为 \(n\) 次实系数多项式,满足 \(\forall x \in [-1,1],\quad |P(x)|\in [-1,1]\),则 \(\forall x \in [-1,1],|P'(x)| \leq n^{2}\)

最后我们得到:
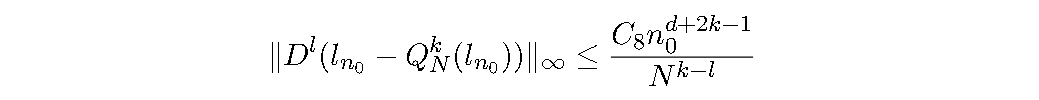
其中 \(C_8\) 仅依赖于 \(k\) 和 \(d\).
接下来就是用 ReLU-(k-1) 网络表示样条插值函数
4. 表达插值样条函数