欧拉回路和欧拉路径

1 欧拉回路

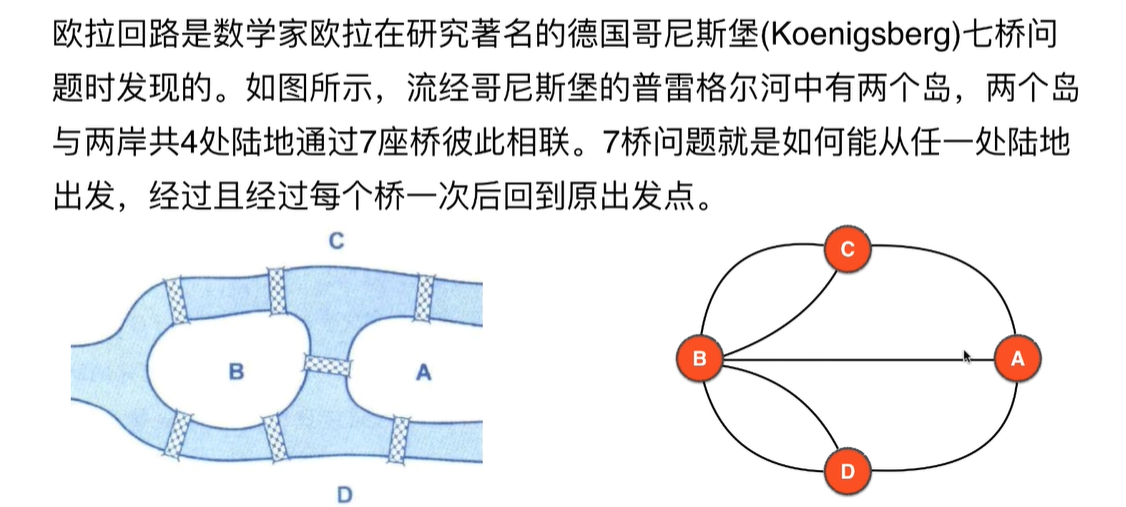
欧拉回路的起源

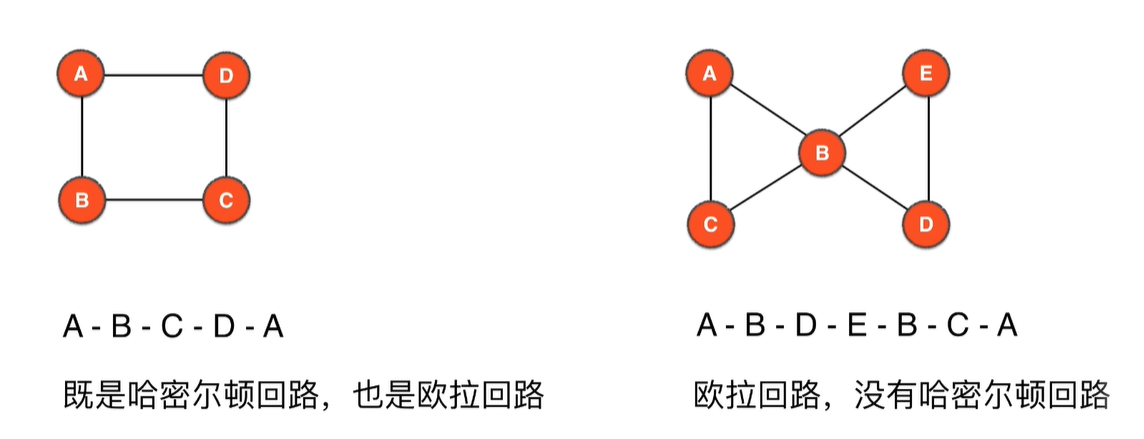
欧拉回路与哈密尔顿回路的区别

经过所有顶点的回路不一定经过所有边。即哈密尔顿回路不一定是欧拉回路

哈密尔顿回路：从一个点出发，沿着边行走，经过每个顶点恰好一次，之后再回到出发点
欧拉回路：从一个点出发，沿着边行走，经过每条边 恰好一次，之后再回到出发点

有哈密尔顿回路不一定有欧拉回路

如下图右侧的图中，所有的实现组成了哈密尔顿回路，但是并没有经过所有边，即不是欧拉回路

有欧拉回路不一定有哈密尔顿回路

欧拉回路要求每条边只能遍历一次，但是每个点可以遍历多次

2 欧拉回路的存在性及证明

欧拉回路存在的性质

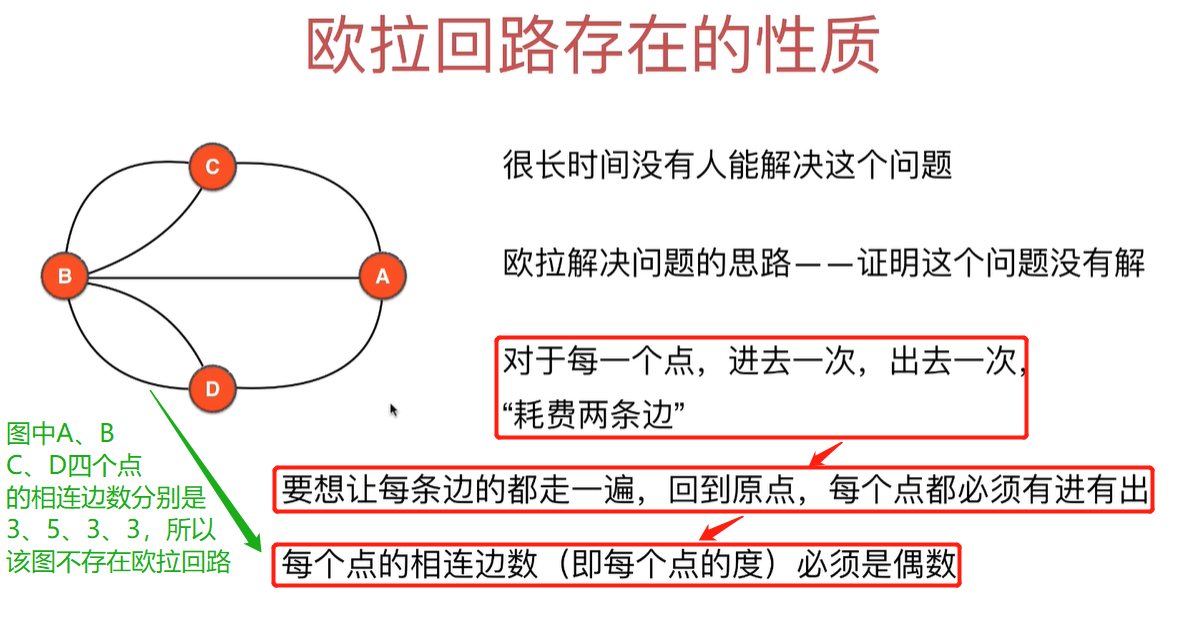
欧拉回路存在的充要条件

注意以下几个条件

无向
联通
每个点的度都是偶数

证明：图中每个点的度(临边数)是偶数--->图存在欧拉回路

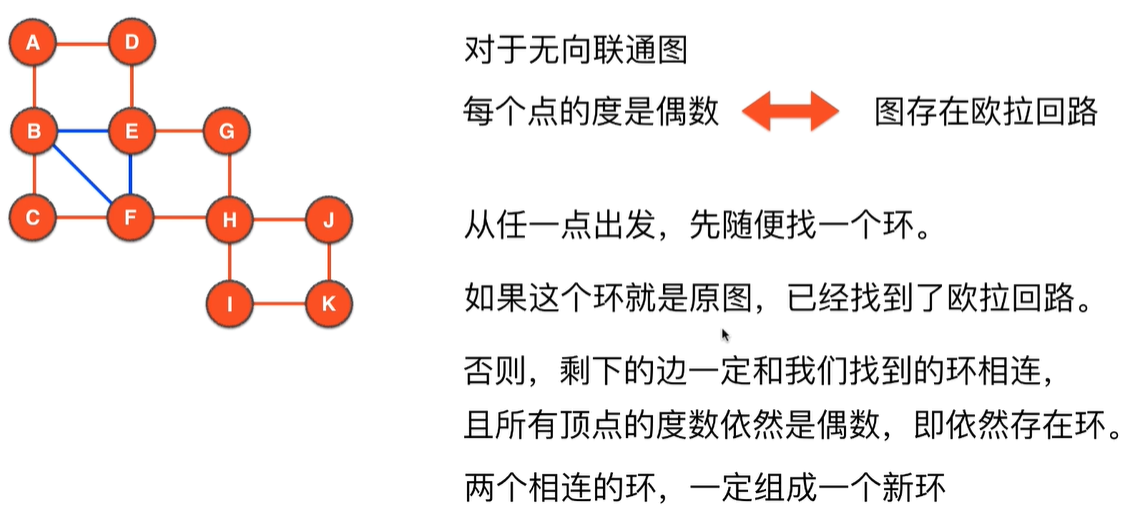
图中每个点的度是偶数则图存在欧拉回路

最终定论

对于无向联通图，如果每个点的度是偶数，则图中存在欧拉回路，反过来同样成立

3 实现`欧拉回路存在性判断`的代码

见实现代码

/**
 * 判断图中是否有欧拉回路
 */
public boolean hasEulerLoop() {
    // 1.检测联通性
    GraphDFS4ConnectedComponents cc = new GraphDFS4ConnectedComponents(graph);
    if (cc.getConnectedComponentCount()>1){
        // 多于一个联通分量肯定就不包含欧拉回路了
        return false;
    }
    // 2.所有的点的度必须都是偶数
    for (int v = 0; v < graph.V(); v++) {
        if (graph.degree(v)%2==1){
            // 如果有一个顶点的度是奇数，直接返回false
            return false;
        }
    }
    return true;
}

4 求解欧拉回路的3个算法

回溯法：指数级时间复杂度，不可用
Fleury算法：基于贪心算法。时间复杂度是多项式级O((V+E)^2)近似为O(E^2)
- 有多条边的时候，不走桥
- 对每一个邻边，判断一下是否是桥(桥的查找可以参考第8章)
- 不能预处理哪些是桥，只能每到一个点再进行判断邻边是否石桥，因为Fleury算法会动态删除边
Hierholzer算法：时间复杂度是O(V+E)近似等于O(E)

随便从图中找一个环，并把环中的边删除，如果剩下的边可以组成环并且和删掉的环有交点，则把这两个环加起来就是欧拉路径。遇到没有临边的点就把这个点加入到最终的欧拉回路中，因为每个边走一次回退一次所以时间复杂度是O(E)

5 Hierholzer算法模拟

用下图来模拟算法的详细执行过程

基于两个栈来完成

curPath记录向前访问的路径
loop记录点没有临边时(过程中被删除了)从curPath中弹出的顺序，即为欧拉路径

注意

1.邻接点访问是从小到大地，因为邻接点矩阵是用TreeSet存地，每访问一个点就压入curPath中
2.当一个顶点没有邻接点时就进行回退，并把回退的点压入到loop中，直到回退到有邻接点的顶点，回退是纯栈的动作，不需要有邻边
3.欧拉回路的寻找过程中顶点是可以重复访问地，不像哈密尔顿回路
4.边用实线表示，虚线表示边已经删除
5.下面遍历过程中的"回退"即不断从栈中弹出栈顶元素

详细遍历过程如下

1.访问A，即把A压入curPath栈，此时curPath=[A]，A的邻接点有B和C，B序号小，接下来访问B
2.访问B，即把B压入curPath栈，此时curPath=[A, B]，删除边AB，B的邻接点此时只剩CDE了(因为边A-B被删除了)，C序号较小，接下来访问C
3.访问C，即把C压入curPath栈，此时curPath=[A, B, C]，删除边BC，C的邻接点此时只剩A(因为边B-C被删除了)，接下来访问A
4.访问A，即把A压入curPath栈，此时curPath=[A, B, C, A], 删除边CA，A此时已经没有邻接点，所以需要回退A
5.回退A，即把A从curPath栈中出栈，并压入loop栈，此时curPath=[A, B, C]，loop=[A]，此时回退到C，C也已经没有邻接点，需要回退C
6.回退C，即把C从curPath栈中出栈，并压入loop栈，此时curPath=[A, B]，loop=[A, C]，此时回退到B，B还有邻接点D、E，所以下面访问D
7.访问D，即把D压入curPath栈，此时curPath=[A, B, D]，删除边BD，D的邻接点此时只有E(因为边B-D已经被删除)，所以接下来访问E
8.访问E，即把E压入curPath栈，此时curPath=[A, B, D, E]，删除边DE，E的邻接点此时只有B(因为边D-E已经被删除)，所以接下来访问B
9.访问B，即把B压入curPath栈，此时curPath=[A, B, D, E, B], 删除边E-B，B此时已经没有邻接点，所以需要回退B
10.回退B，即把B从curPath栈中出栈，并压入loop栈，此时curPath=[A, B, D, E]，loop=[A, C, B]，此时回退到E，所以下面访问E
11.回退E，即把E从curPath栈中出栈，并压入loop栈，此时curPath=[A, B, D]，loop=[A, C, B, E]，此时回退到D，所以下面访问D
12.回退D，即把D从curPath栈中出栈，并压入loop栈，此时curPath=[A, B]，loop=[A, C, B, E, D]，此时回退到B，所以下面访问B
13.回退B，即把B从curPath栈中出栈，并压入loop栈，此时curPath=[A]，loop=[A, C, B, E, D, B]，此时回退到A，所以下面访问A
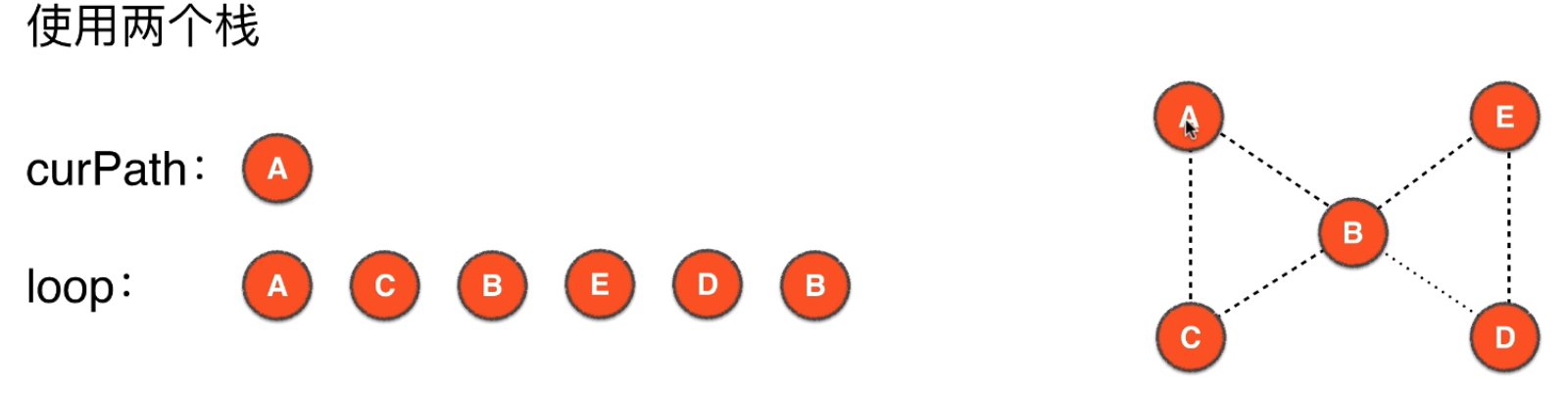
14.回退A，即把A从curPath栈中出栈，并压入loop栈，此时curPath=[]，loop=[A, C, B, E, D, B, A]，此时curPath中为空，loop中存储地即为欧拉回路
15.把栈loop元素依次出栈即得到欧拉回路的详细路径。实际欧拉回路正着看反着看都是可以的~~