torch交叉熵损失-526互联

torch交叉熵损失

torch交叉熵损失

交叉熵其实就是运用了熵的概念先把模型转化为熵的数值然后用数值去比较模型之间的差异。

熵的理解

熵代表了信息量的多少，或者数据的混乱程度。

如果熵比较大(即平均编码长度较长)，意味着这一信息有较多的可能状态，相应的每个状态的可能性比较低；因此每当来了一个新的信息，我们很难对其作出准确预测，即有着比较大的混乱程度/不确定性/不可预测性。

信息量

信息量的大小和事件发生的概率成反比。

信息的三个性质

1.事件发生的概率越低，信息量越大;
2.事件发生的概率越高，信息量越低;
3.多个事件同时发生的概率是多个事件概率相乘，总信息量是多个事件信息量相加。
根据性质3，可以知道使用对数形式可以满足性质需求，因此信息量的表达如下

信息量的表达

\[I(x)=-log(P(x)) \]

其中P(x)表示为, 时间x的发生概率

信息熵

信息量度量的是一个具体事件发生所带来的信息，而信息熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。

\[H(X)=-\sum_{i=1}^{n}P(x_{i})log(P(x_{i})) \]

其中P(x)表示为, 时间x的发生概率

总而言之，信息熵是用来衡量事物不确定性的。信息熵越大，事物越具不确定性，事物越复杂。

熵就是定义成对这个系统求期望-通常也有下面这种写法

\[Entropy=-\sum_{i=1}^{n}P(x_{i})log(P(x_{i})) = E_{x\sim p}\left [ -log(P(x_{i})) \right ] \]

相对熵

相对熵（relative entropy），又被称为Kullback-Leibler散度（KL散度）或信息散度（information divergence）是两个概率分布（probability distribution）间差异的非对称性度量。在信息理论中，相对熵等价于两个概率分布的信息（Shannon entropy）的差值。

可以理解为对于同一个随机变量x，有两个概率分布，判断这两个概率分布得差异。假设两个概率分布对应为p(x),q(x), 如何表示这两个分布得差异，我们可以使用相对熵（散度）判断，于是相对熵产生。

p(x)分布的信息熵为：

\[H_{pp}(X)=-\sum_{i=1}^{n}P(x_{i})log(P(x_{i})) \]

q(x)分布的信息熵为：

\[H_{pq}(X)=-\sum_{i=1}^{n}P(x_{i})log(Q(x_{i})) \]

当使用Q(x)拟合P(x)时,相对熵为

\[H_{pq}(X)-H_{pp}(X) \]

计算得到

\[\begin{matrix} H_{pq}(X) -H_{pp}(X) \\ =(-\sum_{i=1}^{n}P(x_{i})log(Q(x_{i})))-(-\sum_{i=1}^{n}P(x_{i})log(P(x_{i}))) \\ =\sum_{i=1}^{n} P(x_{i})log(\frac{P(x_{i})}{Q(x_{i})} ) \end{matrix} \]

P(x)为样本真实分布，Q(x)为预测分布

KL散度越小，表示P(x) 与Q(x)的分布更加接近，可以通过反复训练Q (x)来使Q (x) 的分布逼近P(x)。

关于相对熵的几点说明

KL散度不是一个对称量 $$D_{KL}(P||Q) \ne D_{KL}(Q||P) $$

KL散度的值始终 ≥ 0 ，当且仅当 P(x)=Q(x)时等号成立

交叉熵

\[CrossEntropy=-\sum_{i=1}^{n}P(x_{i})logQ(x_{i})=E_{x\sim P}\left [ -logQ(x) \right ] \]

交叉熵的函数和相对熵（KL散度）较为相似。

\[\begin{matrix} \because CrossEntropy=-\sum_{x}^{}P(x)logQ(x) \\ = -\sum_{x}^{} P(x) \left [ logP(x)+ log\frac{Q(x)}{P(x)} \right ] \\ =H(P)+ D_{KL}(P||Q) \end{matrix} \]

交叉熵=P的信息熵+相对熵(散度)

所有有交叉熵>=熵

在训练网络的场景下，我们可以将近似分布 Q(x) 看作是网络的实时输出，而我们的目的是通过训练使得 Q(x) 尽量逼近真实分布 P(x)，根据上文可知，等价于最小化 $$D_{KL}$$

真实分布 P 并不随参数变化，所以它的熵 H(P) 是一个固定值，所以KL散度的大小其实只由交叉熵决定，所以最小化 $$D_{KL}(P||Q)$$ 等价于最小化，最后结果。

交叉熵损失函数

多分类交叉熵损失

多标签分类任务，即一个样本可以有多个标签

对多标签分类中的某一类单独分析，真实分布 P 是一个二项分布，可能的取值为0或者1，而网络预测的分布 Q 可以理解为标签是1的概率。所以某一类别的交叉熵损失函数为：

\[Loss= -y \hat{y} -(1-y)log (1-\hat{y} ) \]

二分类交叉熵(单标签分类任务)

在二分的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为 p 和 1−p

假设真实分布为 $$Y$$ ，网络输出的分布为 $$\hat{Y} $$

\[Loss=-\sum_{i=1}^{n} y_{i} log \hat{y_{i}} \]

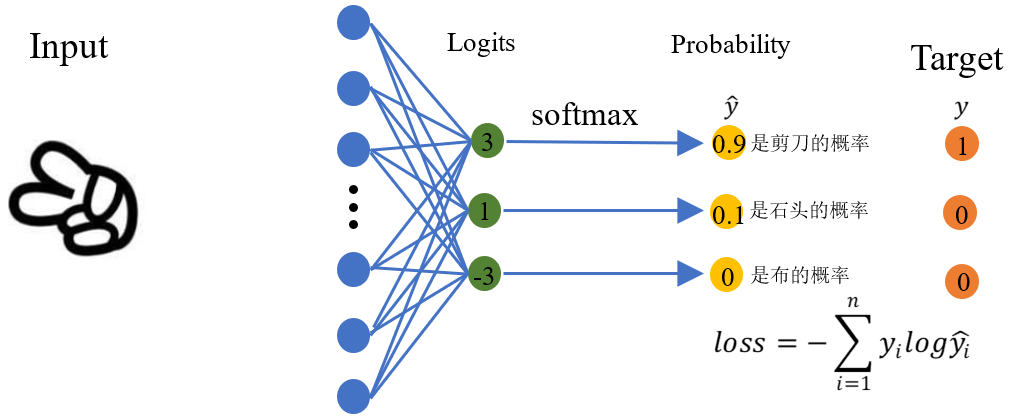
实现和应用

1.先得到网络输出， pred = model(x)，model可以用简单的fc为例
2.对pred进行softmax处理，得到概率P
3.根据真实标签label，得到yi 以及对应的Pi
4.将这些对应的Pi求log，再负号，求和
5.除以batch

numpy实现

"""
batch=3, nc = 4
"""
import numpy as np

target = np.array([
    [-1.0606, 1.5613, 1.2007, -0.2481],
    [-1.9652, -0.4367, -0.0645, -0.5104],
    [0.1011, -0.5904, 0.0243, 0.1002]
])

label = np.array([0, 2, 1])

def np_softmax(arr):
    assert len(arr.shape) == 2
    arr_exp = np.exp(arr)
    arr_sum = np.sum(arr_exp, axis=1)  # (3,4) -->(3,)
    arr_sum = arr_sum[:, None]  # 增加维度，才可以通过广播，进行矩阵除法。(3, )-->(3, 1)
    return arr_exp / arr_sum


def np_onehot(nc, true_label):
    """
    param nc: nc代表划分的类别数目
    param true_label: 传入的标签 shape :（batch, )
    return: 返回一个(batch, nc)形式的one_hot变量
    """
    tmp = np.arange(nc)
    tmp = tmp[None, :]  # 增加行的维度，[0,1,2,3] -->[[0, 1, 2, 3]] 。后续才能广播，每一行都是0,1,2,3
    true_label = true_label[:, None]  # 增加列的维度，[0, 2, 1] -->[[0],[2],[1]] 。按照列广播
    ans = tmp == true_label  # 自动广播，返回(batch, nc)形式，为True或False
    return ans.astype(int)  # bool --> int


# 1.对预测结果softmax处理
target_soft = np_softmax(target)
# 2. 取log对数
target_log = np.log(target_soft)
# 3. one-hot变量
label_one = np_onehot(4, label)
# 4. python矩阵乘法，按照元素相乘； 取负数  ， 负对数
res = -target_log * label_one
# 5. 按照列求和， 取均值
loss = np.mean(np.sum(res, axis=1))

print(loss)

pytorch实现

torch实现

class torch.nn.CrossEntropyLoss(weight=None, size_average=None,
                                ignore_index=-100, reduce=None, 
                                reduction='elementwise_mean')
nn.functional.cross_entropy(input, target, 
                            weight=None, size_average=None, 
                            ignore_index=- 100, reduce=None, 
                            reduction='mean', label_smoothing=0.0)

函数参数

weight(Tensor):  	对每个类别的手动重新缩放权重		
size_average(bool): 当 reduce=True 时有效。为 True 时，返回的 loss 为平均值;为 False 时，返回的各样本的 loss 之和。
reduce(bool): 		返回值是否为标量，默认为 True。
ignore_index(int): 	忽略某一类别，不计算其 loss，其 loss 会为 0，
					并且，在采用 size_average 时，不会计算那一类的 loss，除的时候的分母也不会统计那一类的样本。

将输入经过 softmax 激活函数之后，再计算其与 target 的交叉熵损失。即该方法将 nn.LogSoftmax() 和 nn.NLLLoss()进行了结合。严格意义上的交叉熵损失函数应该是 nn.NLLLoss()。

def cross_entropy(input, target, weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean'):

    if size_average is not None or reduce is not None:

        reduction = _Reduction.legacy_get_string(size_average, reduce)

    return nll_loss(log_softmax(input, 1), target, weight, None, ignore_index, None, reduction)

可以看出softmax + log + NLLloss = crossEntropyLoss。

import torch
import numpy as np
import torch.nn as nn

criterion = nn.CrossEntropyLoss()

target = np.array([
    [-1.0606, 1.5613, 1.2007, -0.2481],
    [-1.9652, -0.4367, -0.0645, -0.5104],
    [0.1011, -0.5904, 0.0243, 0.1002]
])
target = torch.tensor(target)
label = torch.tensor([0, 2, 1])
res = criterion(target, label)
print(res)

pytorch等价实现

import torch
import numpy as np
import torch.nn as nn


target = np.array([
    [-1.0606, 1.5613, 1.2007, -0.2481],
    [-1.9652, -0.4367, -0.0645, -0.5104],
    [0.1011, -0.5904, 0.0243, 0.1002]
])
target = torch.tensor(target)
label = torch.tensor([0, 2, 1])

# 先取softmax，再取log操作

m = nn.LogSoftmax(dim=1)
# The negative log likelihood loss. It is useful to train a classification
# problem with `C` classes
loss = nn.NLLLoss()


tmp = m(target)
output = loss(tmp, label)
print(output)