Description
1494. Parallel Courses II (Hard)
You are given an integer n, which indicates that there are n courses
labeled from 1 to n. You are also given an array relations
where relations[i] = [prevCoursei, nextCoursei], representing a
prerequisite relationship between course prevCoursei and course
nextCoursei: course prevCoursei has to be taken
before course nextCoursei. Also, you are given the integer
k.
In one semester, you can take at most k courses as long as you have
taken all the prerequisites in the previous semesters for the courses you are
taking.
Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.
Example 1:
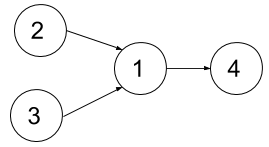
Input: n = 4, relations = [[2,1],[3,1],[1,4]], k = 2 Output: 3 Explanation: The figure above represents the given graph. In the first semester, you can take courses 2 and 3. In the second semester, you can take course 1. In the third semester, you can take course 4.
Example 2:
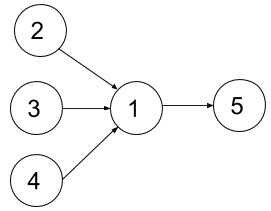
Input: n = 5, relations = [[2,1],[3,1],[4,1],[1,5]], k = 2 Output: 4 Explanation: The figure above represents the given graph. In the first semester, you can only take courses 2 and 3 since you cannot take more than two per semester. In the second semester, you can take course 4. In the third semester, you can take course 1. In the fourth semester, you can take course 5.
Constraints:
1 <= n <= 151 <= k <= n0 <= relations.length <= n * (n-1) / 2relations[i].length == 21 <= prevCoursei, nextCoursei <= nprevCoursei != nextCoursei- All the pairs
[prevCoursei, nextCoursei]are unique. - The given graph is a directed acyclic graph.
Solution
This problem readily brings to mind the concept of topological sorting, followed by a greedy approach. However, this approach is erroneous! In essence, this problem is NP-Hard and can only be solved through brute force.
Let's consider the application of state-compressed dynamic programming (DP). The subproblems are relatively straightforward to identify. We start by choosing $1, 2$, followed by selecting $3, 4, 5 $(meeting the prerequisites). We can use a binary number, $to$$study$, to represent the set of courses we currently need to study, and $pre[j]$ to represent the set of prerequisite courses for course $j$. The recursive function can be denoted as $dfs(to$$study, pre)$.
Within this recursive function, we first calculate the set of courses $tmp$ that can be studied at the moment:
for (int i = 0; i < n; ++i) {
if ((((1 << i) & to_study) != 0) && (pre[i] & to_study) == 0) {
// Indicates that i is in to_study and its prerequisite courses have been studied (or it has no prerequisites)
tmp = (tmp | (1 << i));
++cnt;
}
}
If the number of courses $cnt$ in $tmp$ is less than or equal to k, we can directly study all the courses in the $tmp$ set. Otherwise, we iterate through the subsets of $tmp$. If the number of courses $m$ in subset $i$ satisfies $m <= k$, we study that subset. In the next recursive call, the courses to be studied can be represented as $to$_$study \oplus i$.
For a method to enumerate subsets, refer to Bitwise Operations and Sets.
In C++, the library function to count the number of $1$ bits in a binary number is __builtin_popcount(i).
Code
class Solution {
public:
static auto dfs(int to_study, vector<int> &cache, int full, vector<int> &pre, int n, int k) -> int {
if (to_study == 0) {
return 0;
}
if (cache[to_study] != -1) {
return cache[to_study];
}
int studied = (to_study ^ full);
int count = 0; // Count the number of courses that can be studied
int tmp = 0; // Courses to be studied in this recursive call
for (int i = 0; i < n; ++i) {
if ((((1 << i) & to_study) != 0) && (pre[i] & to_study) == 0) {
// Indicates that i is in to_study and its prerequisite courses have been studied (or it has no prerequisites)
tmp = (tmp | (1 << i));
++count;
}
}
if (count <= k) {
cache[to_study] = dfs(to_study ^ tmp, cache, full, pre, n, k) + 1;
return cache[to_study];
}
int result = INT_MAX;
for (int i = tmp; i != 0; i = (i - 1) & tmp) {
if (__builtin_popcount(i) <= k) {
result = min(result, dfs(to_study ^ i, cache, full, pre, n, k) + 1);
}
}
cache[to_study] = result;
return cache[to_study];
}
int minNumberOfSemesters(int n, vector<vector<int>> &relations, int k) {
vector<int> pre(n);
for (auto &vec : relations) {
int x = vec[0] - 1, y = vec[1] - 1; // Adjusting indices to start from 0 to n-1
pre[y] = (pre[y] | (1 << x));
}
int full = (1 << n) - 1; // Full set
vector<int> cache(1 << n, -1);
return dfs(full, cache, full, pre, n, k);
}
};