涉及知识点：DP

前言

可能是最简单的解法了。

这种做法太巧妙了，也启发了我们一些其他的类似二元字符串的问题。

题面

Link

给你一个 \(n\) 个字符的字符串 \(s\)，该字符串只由小写字母 \(a\) 和 \(b\) 组成，你能进行如下两种操作：

将子串 aa 替换为 b。
将子串 bb 替换为 a。

请问在进行若干次这样的操作后，问最后可以得到多少种不同的字符串（对 \(1e9+7\) 取模）？

思路

我们可以把 a 用 \(1\) 表示，b 用 \(2\) 表示，可以发现如果这么表示，那么对于任意操作，操作前后字符串的字符和在 \(\bmod 3\) 意义下是相等的。

同时我们也可以发现，若干操作后生成的字符串的每个字符一定能对应原串的一段区间，并且结合刚才我们新定义的表示法，原串区间的字符和在模 \(3\) 意义下与最终的字符相等。即对于原串的任意区间，如果区间和模 \(3\) 意义下等于 \(1\)，则该区间最后可以通过一系列操作最后变为一个字符 a；等于 \(2\) 同理为 b；等于 \(0\) 则说明这段区间无法缩成一个字符。

我们考虑 DP 计数，设 \(f[i]\) 表示原串 \([1,i]\) 的区间最后能生成多少种不同的字符串，则答案为 \(f[n]\)。

那我们考虑如何转移，我们令 \(i\) 的前缀和在 \(\bmod 3\) 意义下为 \(str[i]\)，设当前遍历到 \(i\)，首先我们需要判断 \([1,i]\) 能否被直接缩成一个字符（这种情况之前肯定没有处理过），如果 \(str[i]\neq0\)，就把 \(f[i]\) 的初值设为 \(1\)，否则为 \(0\)。

然后我们需要从上一个 \(str[j]\neq str[i]\) 的 \(j\) 转移，\(f[i]+=f[last[str[i]]]\)，表示我们在 \(f[j]\) 的基础上再将 \((last[str[i]],i]\) 这个区间合成为一个字母。最后再更新 \(last\) 即可。

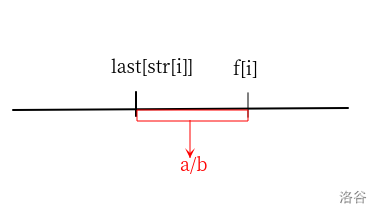
为什么需要 \(str[j]\neq str[i]\)？

如下图，由于 \(str[i]\) 是模 \(3\) 意义下的前缀和，如果 \(str[j]=str[i]\)，则说明 \((j,i]\) 这个区间内的字符和为 \(0\)，不能缩成一个字符。

可以发现，这样转移是不会遗漏或多算的。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL P=1e9+7;
const int MAXN=1e5+5;
int n,a[MAXN],f[MAXN],last[3];
string str;
int main(){
    cin>>str;
    n=str.size();
    bool flag=1;
    for(int i=1;i<=n;i++){
        a[i]=(str[i-1]=='a'?1:2);
        if(i>1 && str[i-1]==str[i-2]) flag=0;
    }
    if(flag){
        puts("1");
        return 0;
    }
    for(int i=1;i<=n;i++){
        a[i]=(a[i]+a[i-1])%3;
    }
    for(int i=1;i<=n;i++){
        f[i]=(int)(a[i]>=1);
        for(int j=0;j<3;j++){
            if(j!=a[i]) f[i]=(f[i]+f[last[j]])%P;
        }
        last[a[i]]=i;
    }
    cout<<f[n]<<endl;
    return 0;
}