「杂题乱写」AGC 002
点击查看目录
A | Range Product
分讨不解释。
B | Box and Ball
直接按题意模拟。
C | Knot Puzzle
不难发现解开最后一下仍然需要两个绳子长度 \(\ge l\),那么考虑找到两条相邻且长度满足条件的绳子作为最后一个解开的,然后从两边向中间解。
D | Stamp Rally
Kruskal 重构树或是可持久化并查集+整体二分。
都不会,有空再补。
E | Candy Piles
博弈论神仙题。
图都来源于官方题解。
首先对数组排序,然后可以把数组转化成这样:
(以 \(a = (7, 7, 7, 6, 4, 4, 4, 2, 2)\) 为例)
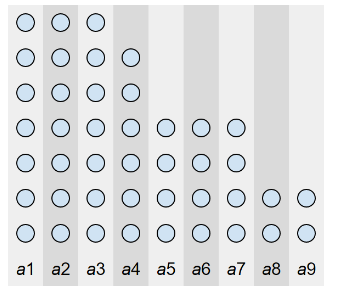
不难发现两种操作等价于删去一行/一列:
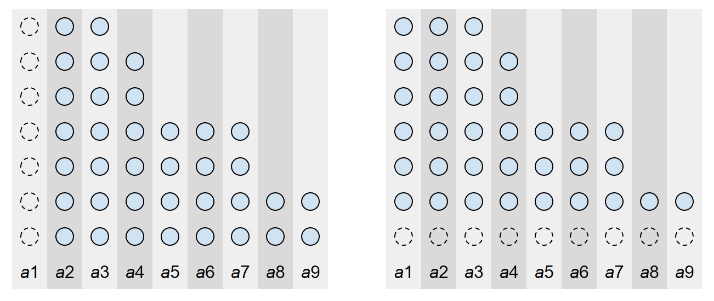
进一步转化一下,两种操作等价于在这个网格中向上/向右走一步:
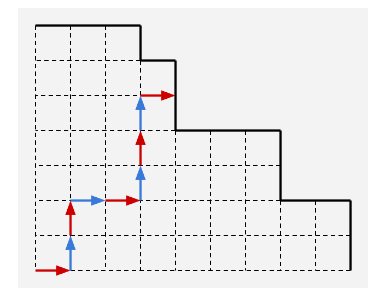
先手从左下角走第一步,当到达边界的时候输掉。
那么可以在网格上画出必胜点(红色)和必败点(蓝色),即从这个点出发的先手是必胜还是必败:
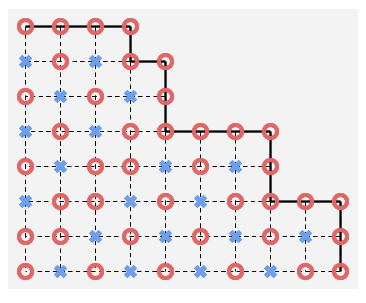
不难发现先后手分别往左和往右走一步是否必胜不变,因此一条斜线上是否必胜都一样。
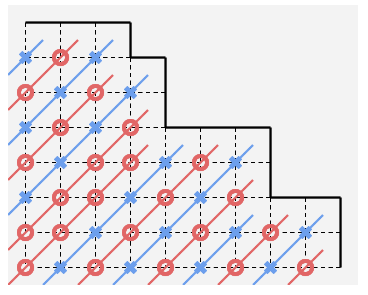
那么搞一个左下角为出发点的最大正方形,考虑判断这个正方形右上角是否为必胜点。
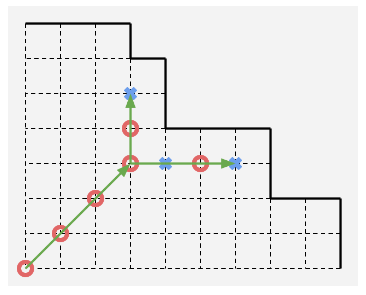
判断很好搞,因为此时只有纯向上走和纯向右走两个选择,所以如果有一种方法可以走奇数步则这个点是一个必胜点。
点击查看代码
const ll N = 1e5 + 10;
namespace SOLVE {
ll n, a[N], k, ans;
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline void In () {
n = rnt ();
_for (i, 1, n) a[i] = rnt ();
return;
}
inline void Solve () {
std::sort (a + 1, a + n + 1, [](ll x, ll y) { return x > y; });
_for (i, 1, n) if (i + 1 > a[i + 1]) { k = i; break; }
ll l = 0;
while (a[k + l + 1] == k) ++l;
ans = (l & 1) || ((a[k] - k) & 1);
return;
}
inline void Out () {
puts (ans ? "First" : "Second");
return;
}
}
F | Leftmost Ball
DP 计数题。
设 \(f_{i, j}\) 表示放了 \(i\) 个白球,放了 \(j\) 种颜色的所有球的方案数。
考虑放一个白球,只能放在第一个空位,方案数 \(f_{i - 1, j}\)。
考虑放一种颜色的所有球。首先有 \(n - j + 1\) 种颜色可以用,然后我们有 \(k - 2\) 个自由球可以放,一个球变成了白球,还有一个球为了保证不会被重复计算,必须放在第一个空位。 此时有 \(n * k - i - (j - 1)(k - 1) - 1\) 个空位,那么方案数为 \((n - j + 1)\dbinom{n * k - i - (j - 1)(k - 1) - 1}{k - 2}f_{i, j - 1}\)。
点击查看代码
const ll N = 2e3 + 10, P = 1e9 + 7;
namespace SOLVE {
ll n, k, f[N], fac[N * N], inv[N * N], ans;
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline ll FastPow (ll a, ll b) {
ll ans = 1;
while (b) {
if (b & 1) ans = ans * a % P;
a = a * a % P, b >>= 1;
}
return ans;
}
inline ll C (ll x, ll y) { return fac[x] * inv[y] % P * inv[x - y] % P; }
inline void Pre () {
fac[0] = 1;
_for (i, 1, 4000000) fac[i] = fac[i - 1] * i % P;
inv[4000000] = FastPow (fac[4000000], P - 2);
for_ (i, 3999999, 0) inv[i] = inv[i + 1] * (i + 1) % P;
return;
}
inline void In () {
n = rnt (), k = rnt ();
return;
}
inline void Solve () {
Pre ();
f[0] = 1;
_for (i, 1, n) {
_for (j, 1, i) {
ll x = (n - j + 1) * C (n * k - i - (j - 1) * (k - 1) - 1, k - 2) % P * f[j - 1] % P;
f[j] = (f[j] + x) % P;
}
}
return;
}
inline void Out () {
printf ("%lld\n", k == 1 ? 1 : f[n]);
return;
}
}