CF1268D Invertation in Tournament 题解

传送门

CF1442F Differentiating Games

题目大意

给定一个竞赛图，一次操作可以将一个节点相连的所有边方向翻转。求让图强连通的最小操作次数。

竞赛图是一个无向完全图的每条边分配方向后的图。

思路

因为我们需要图 \(G\) 强连通，所以想到求出 scc 并缩点。

可以发现，我们进行翻转操作时，只有保证不破坏原有的 scc，才可以保证操作次数最小。

又因为我们能够合并 scc，我们肯定可以拆散 scc。

题目给了竞赛图的条件，思考怎么利用它。

不妨设我们现在有一个 scc，它的大小为 \(n\)。

我们可以猜测，在 \(n \not= 3\) 时，存在一个点翻转之后不会拆散这个 scc。

Q：为什么 \(n \not= 3\)？

A：\(n=3\) 时是一个单向环，显然不成立。

Q：为什么有反例我们还要坚持这条路？

A：如果只是 \(n=3\) 不满足条件，特殊处理不就好了。

\(n=1\) 显然不影响，竞赛图没有重边不存在 \(n=2\)，我们只需要考虑 \(n \ge 4\) 的情况。

设我们用点 \(x\) 拆散了这个 scc，拆散过后 scc 个数为 \(m\)，编号为 \(a_1,a_2,\dots,a_m\)。

\(m=1\)

根本就没有拆散，不用考虑。
\(m=2\)

这时只有两类边，从 \(a_1\) 连向 \(a_2\) 的边和从 \(a_2\) 连向 \(a_1\) 的边。

如果两类都存在，它们就会变成一个 scc，所以我们钦定只存在 \(2\) 类边。

那么翻转之前如图，左边是 \(a_1\)，右边是 \(a_2\)（没有展示所有的边）：

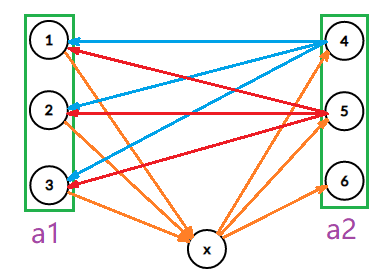
这时如果我们不翻转 \(x\)，而是翻转 \(4\)，那么红色 \(2\) 类边和除连接 \(x \to 4\) 外的橙色 \(1\) 类边就同时存在了。

因为 \(n \ge 4\)，scc 大小不为 \(2\)，所以我们一定有一个 scc 大小大于等于 \(3\)，那么翻转这个 scc 中的点就可以保证不拆散原来的 scc 了。
\(m \ge 3\)

当 \(a_1,a_m\) 中有任意一个大小大于 \(1\) 时同 \(m=2\)，只需将 \(a_m\) 看作 \(a_2\) 即可。

那我们只需要考虑 \(a_1,a_m\) 大小都为 \(1\) 的情况。

我们将 \(a_2,a_3,\dots,a_{m-1}\) 看作一个点 \(y\)，如图：

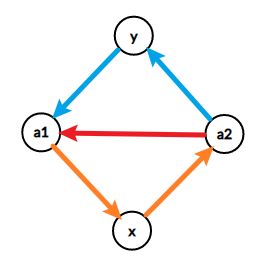
这时我们不翻转 \(x\)，而是翻转 \(y\)，就可以让任意 \(s,t\)，有路线 \(s \to a_1 \to y \to a_2 \to t\)。

也就是说，我们选择 \(a_2,a_3,\dots,a_{m-1}\) 中的任意一个点翻转都不会拆散原来的 scc。

那到这里我们就证完了。

我们观察上面的证明可以发现，如果我们将过程逆转，从 拆散 到 合并，同样是可以的。这提示我们，存在一个点使得翻转这个点之后图强连通。

那么 \(n\) 至少为多少？

\(m=1\)

不用翻转。
\(m=2\)

首先根据上面结论，一个大小大于等于 \(4\) 的 scc 才能够有至少一个点让我们翻转。那么只有当 \(n \ge 7\) 的时候才可以保证有一个 scc 大小大于等于 \(4\)，所以 \(n\) 至少为 \(7\)。
\(m \ge 3\)

不难发现，在这种情况下，\(n\) 至少为 \(3\)。

取上述最大值，\(n\) 至少为 \(7\)。

那么 \(n \le 6\) 的情况呢？我们可以直接 \(2^n\) 暴力枚举翻转的点集即可。

最后，根据竞赛图的兰道定理，我们可以推出，一个竞赛图非强连通的充要条件是：将其顶点按出度从小到大排序，存在 \(k < n\) 使得前 \(k\) 个顶点的出度之和等于 \(C_k^2\)。

这样我们就可以 \(O(n \log n)\) 完成一次判断，总复杂度 \(O(n^2 \log n)\)。

代码实现

#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(ll i=(a);i<=(b);++i)
#define Rep(i,a,b) for(ll i=(a);i>=(b);--i)
#define Gra(i,x) for(ll i=fir[x];i;i=nxt[i])
#define Yes printf("YES\n")
#define No printf("NO\n")
#define pb push_back
#define lson rt<<1
#define rson rt<<1|1
#define ED printf("\n")
#define zero printf("0\n")
#define one printf("-1\n")
const ll N=2e3+10;
using namespace std;
//const ll p=1e9+7;
const ll p=998244353;
ll ksm(ll a,ll b){ll bns=1;while(b){if(b&1)bns=bns*a%p;a=a*a%p;b>>=1;}return bns;}
void PLUS(ll &a,ll b){a=a+b>=p?a+b-p:a+b;}

ll n;
ll minn=1e9,cnt;//最小操作次数和方案数量
ll a[N][N];//邻接矩阵

ll out[N];//出度
ll tmp[N];//出度
bool check(){//判断是否强连通
	//统计出度
	For(i,1,n)tmp[i]=out[i];//备份
	sort(tmp+1,tmp+n+1);//排序
	//判断强连通
	ll s=0;//前缀和
	For(i,1,n-1){
		s+=tmp[i];
		if(s==i*(i-1)/2)return false;
	}
	return true;
}

void rev(ll x){//翻转x
	For(i,1,n){
		out[x]-=a[x][i],out[i]-=a[i][x];
		a[x][i]^=1,a[i][x]^=1;
		out[x]+=a[x][i],out[i]+=a[i][x];
	}
}

namespace sub1{
	void dfs(ll x,ll ans){//暴力
		if(x>n){
			if(check()){
				if(ans<minn)minn=ans,cnt=1;
				else if(ans==minn)cnt++;
			}
			return;
		}
		dfs(x+1,ans);
		rev(x);
		dfs(x+1,ans+1);
		rev(x);
	}
	void solve(){
		dfs(1,0);
		if(minn==1e9)printf("-1");//无解
		else{
			For(i,1,minn)cnt=cnt*i%p;//可以打乱顺序
			printf("%lld %lld",minn,cnt);
		}
	}
}

namespace sub2{
	void solve(){
		if(check()){//答案可以为0
			printf("0 1");
			return;
		}
		For(i,1,n){
			rev(i);
			if(check())cnt++;
			rev(i);
		}
		printf("1 %lld",cnt);
	}
}

void mian(){
	
	scanf("%lld",&n);
	For(i,1,n){
		For(j,1,n){
			scanf("%1lld",&a[i][j]);
		}
	}
	For(i,1,n){
		For(j,1,n){
			out[i]+=a[i][j];//统计出度
		}
	}
	if(n<=6)sub1::solve();//暴力枚举
	else sub2::solve();//根据性质处理
	
}

int main(){
	int T=1;
//	scanf("%d",&T);
	while(T--)mian();
	return 0;
}