关于圣彼得堡悖论的一些思考
记 \(N\) 为 游戏的轮数,则 \(N \sim Ge(\frac{1}{2}),P(N=k)=2^{-k},k=1,2,3,...\)
奖金 \(X=2^N\),\(E(X)=E(2^N)=\sum_{k=1}^{+\infty} 2^k\times 2^{-k}=\sum_{k=1}^{+\infty} 1 = +\infty\)
理论上如果能玩无限轮游戏,便可获得无限的奖金。
下面作模拟:
import random
import matplotlib.pyplot as plt
MaxN = 10000000
def getAward():
award = 1
while(1):
award *= 2
if (random.random() <= 0.5):
break
return award
sumAward = 0
x_v = []
y_v = []
for i in range(0, MaxN):
sumAward += getAward()
x_v.append(i + 1)
y_v.append(sumAward / (i + 1))
plt.xlabel("Count of rounds")
plt.ylabel("Average award")
plt.plot(x_v, y_v)
[<matplotlib.lines.Line2D at 0x1f843cec1c0>]

该算法的期望复杂度为\(O(\sum_{k=1}^{N}\sum_{j=1}^{+\infty})(\frac{1}{2})^j=O(N)\)
通过模拟发现现实中,在有限的游戏轮数的情况下,奖金并不是无限。
随着轮数的增加,平均奖金在逐渐升高。
下面通过引入置信度的方法来大致计算出上面这条曲线的函数。
考虑求条件期望 \(E(X|X\le M)\),其中 \(M\) 是使 \(P\{ X \le M\} \ge 1-p\) 的最大值。
\(1-p\) 即为置信度。
若令 \(p=10^{-3}\),则 \(M=2^{10}=1024\),则 \(E(X|X \le 1024)=10/(1-p) \approx 10\)
考虑 \(n\) 轮的情况。
记 \(X_i\) 表示第 \(i\) 轮的奖金。
则 \(X=X_1+X_2+...+X_n=\mu_n\)。
我们想要知道 \(X/n\) 的相关性质(由于 \(E(X_i)=+\infty\) ,所以不能用辛钦大数定律)
还是考虑计算条件期望 \(E(X/n|X \le M)\),其中 \(M\) 是使 \(P\{ X \le M\} \ge 1-p\) 的最大值,设 \(p=2^{-m}\)。
考虑如何求 \(M\)。
记 \(Y_i\) 为 \(X_i\) 去掉 \(>M\) 之后部分的新的随机变量。
则 \(P\{Y_i=k\}=2^{-k}/(1-2^{-m})\)
\(E(Y_i)=m/(1-2^{-m})\)
\(D(Y_i)=(2^{m+1}-2)/(1-2^{-m})\)
\(n\rightarrow \infty\) 时,对 \(\mu_n\) 成立中心极限定理:
\(P\{\mu_n \le M\}=P\{\frac{\mu_n-nE(x1)}{\sqrt{n\times D(Y_i)}} \le \frac{M-nE(x1)}{\sqrt{n\times D(Y_i)}} \} = \Phi(\frac{M-nE(x1)}{\sqrt{n\times D(Y_i)}})\)
不放令 \(m=30,n=10^7\),解 \(M\) 如下:
from scipy.stats import norm
n = 10000000
m = 30
p = pow(0.5, m)
Ey = m/(1-p)
Dy = (pow(2, m + 1) - 2) / (1 - p)
x = norm.ppf(1 - p)
M = x * pow(n * Dy, 0.5) + n * Ey
print("M = ", M)
M = 1180628405.2149527
解出 \(M\) 后,\(E(X/n|X \le M)\) 就好算了。
可以近似认为就是 \(log M\)
import math
print(math.log(M)/math.log(2))
30.136907811683777
考虑对比两条曲线:
y_v_2 = []
for i in range(0, MaxN):
n = i + 1
M = x * pow(n * Dy, 0.5) + n * Ey
y_v_2.append(math.log(M)/math.log(2))
plt.plot(x_v, y_v, label = "real")
plt.plot(x_v, y_v_2, label = "estimate", color = 'red')
plt.legend()
plt.show()
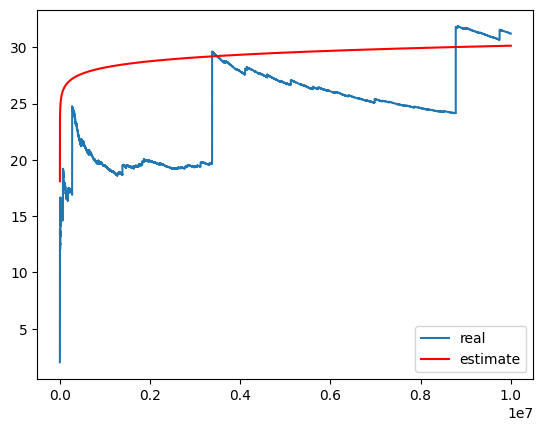
不难发现还挺准的。