一维最小乘积生成树
一维最小乘积:一维可以谈乘积吗?
问题
即普通最小生成树。
解法
大家都会。
可以用 Kruskal 算法或 Prim 算法求解。
二维最小乘积生成树
二维最小乘积:一种不太常见的套路。
问题
P5540 [BalkanOI2011 timeismoney] | 最小乘积生成树
给出一个 \(n\) 个点 \(m\) 条边的无向图,第 \(i\) 条边有两个权值 \(a_i\) 和 \(b_i\) 。
求该图的一棵生成树 \(T\) ,使得 \(\left(\sum_{e\in T}a_e\right)\times\left(\sum_{e\in T}b_e\right)\) 最小。
\(1 \leq n \leq 200,1 \leq m \leq 10000,0 \leq a_i,b_i \leq 255\),\(n,m,a_i,b_i\) 均为整数。
解法
-
第一想法
第一想法肯定是直接用 Kruskal 或 Prim,然而这两个算法都是贪心算法,通过举例,我们发现最小乘积是不能直接贪心的。
-
性质
我们可以发现最优方案其实满足一些性质。
对于一棵生成树 \(T\) ,将其看作二维平面直角坐标系下的点 \((\sum_{e\in T}a_e,\sum_{e\in T}b_e)\),则最优方案对应点一定在下凸壳上。
-
证明
对于不在下凸壳上的方案,其与原点的连线一定交下凸壳于某点,这点一定劣于这个交点,而下凸壳顶点连线上任意一点一定劣于相邻两顶点中的至少一个(画反比例函数证明)。
-
如何找到下凸壳
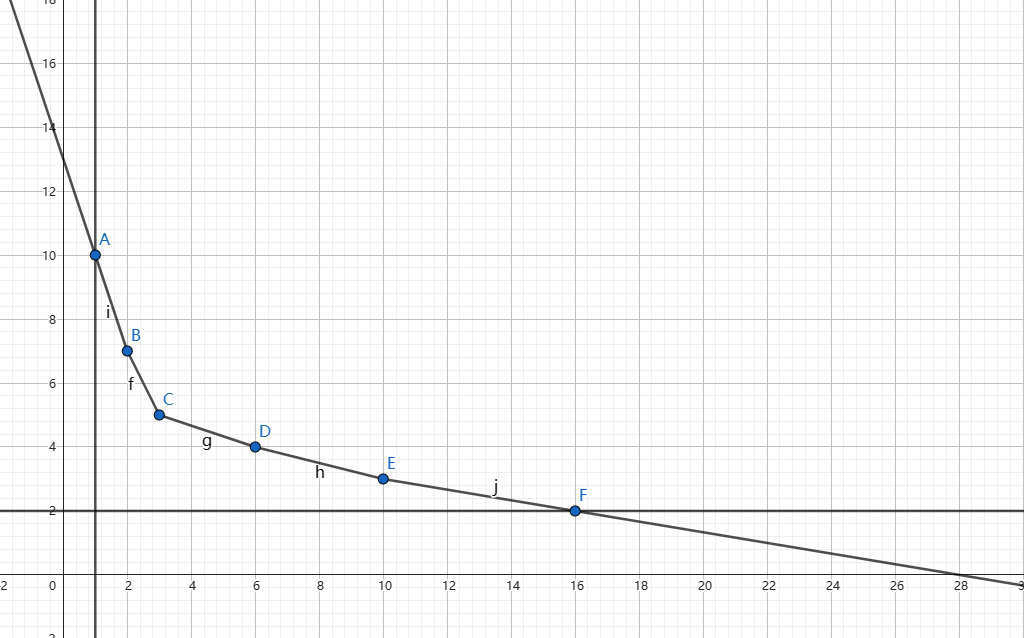
- 首先,平面上大概有 \(\binom{m}{n-1}\) 个点,不能直接加入所有点求下凸壳。
- 所以用一种分治的方法,对于两个已在凸包上的点组成的点对 \(\{A,B\}(x_A<x_B)\),在直线 \(l_{AB}\) 的左下方,且与直线距离最大的 \(C\) 点一定在凸包上。找到 \(C\) 点之后再对 \(\{A,C\}\) 和 \(\{C,B\}\) 分别递归处理。
- 其实这就是二维 QuickHull 法。
-
如何求 \(C\) 点
-
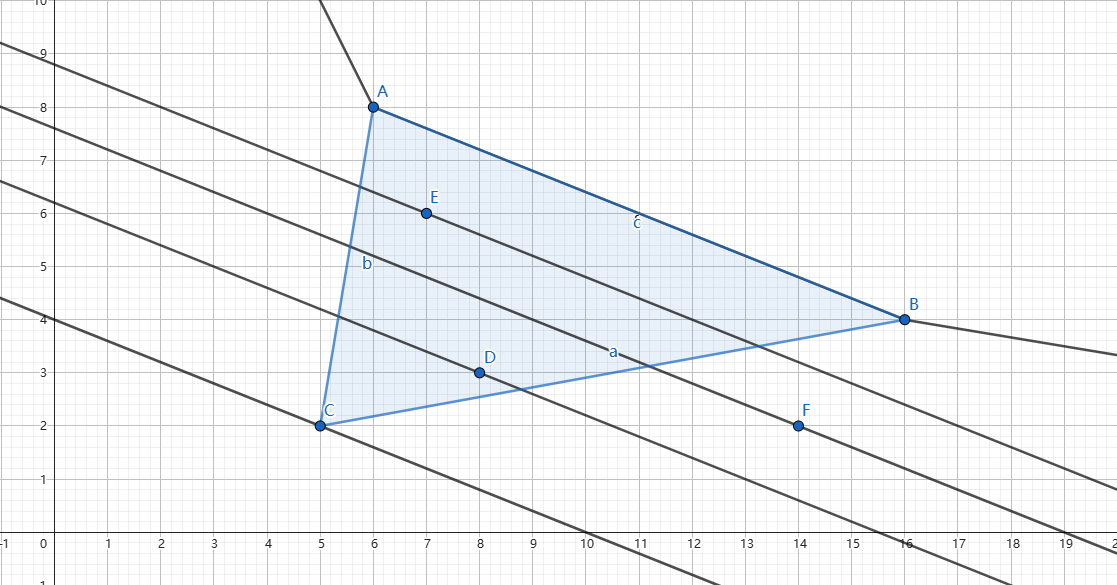
距离最大等价于 \(\triangle{ABC}\) 面积最大,三角形面积可以用向量叉积(也可以认为是铅垂法或割补法)来表示:
\[\begin{aligned} S_{\triangle{ABC}} &= \frac{1}{2}\left|\vec{CA}\times\vec{CB}\right|\\ &= \frac{1}{2}\left|(x_A-x_C)(y_B-y_C)-(x_B-x_C)(y_A-y_C)\right|\\ &= \frac{1}{2}\left|x_Ay_B-x_Ay_C-x_Cy_B+x_Cy_C-x_By_A+x_By_C+x_Cy_A-x_Cy_C\right|\\ &= \frac{1}{2}\left|(y_A-y_B)x_C+(x_B-x_A)y_C+x_Ay_B-x_By_A\right|\\ \end{aligned} \] -
注意到绝对值内必然为负值,要使面积最大,即使 \((y_A-y_B)x_C+(x_B-x_A)y_C\) 最小。以 \((y_A-y_B)a_i+(x_B-x_A)b_i\) 作为第 \(i\) 条边的边权,求最小生成树,即可得到 \(C\) 点。注意在求得后进行检验,若合法则对 \(\{A,C\}\) 和 \(\{C,B\}\) 继续分治,否则说明当前区间内凸包上所有点都已求得。
-
-
初始的 \(A\) 和 \(B\)
对 \(a\) 属性和 \(b\) 属性分别做一次最小生成树即可。
注意一定不能用 \(A(0,+\infty)\) 和 \(B(+\infty,0)\)(然而洛谷数据太水,这种做法也可以通过),如果这样初始化,可能会忽略凸壳上靠近坐标轴的一些点。
-
时间复杂度
-
设 \(h\) 为下凸壳上的点数,则时间复杂度为 \(\Omicron(m\log{m}h)\) 或 \(\Omicron(n^2h)\)。
第一种算法是 \(\Omicron(m\log{m})\) Kruskal,第二种算法是 \(\Omicron(n^2)\) Prim。一般情况下 \(n\) 很小,\(m\) 很大,所以第二种算法更优。
-
有没有更准确的复杂度?
EI 说 \(h\) 是 \(\Omicron((nV)^{\frac{2}{3}})\) 级别的(其中 \(V = \max(a_i,b_i)\),要求 \(a_i\) 和 \(b_i\) 必须为整数),此时最优复杂度为 \(\Omicron(n^{\frac{8}{3}}V^{\frac{2}{3}})\)。
然而我并没有找到 EI 的证明。
-
-
代码
#include <bits/stdc++.h>
using namespace std;
const int N=2e2+5;
const int M=1e4+5;
const int V=(1<<8)+5;
int n,m;
bool vis[N];
struct Edge{
int a,b,x,y;
}edge[M];
struct Point{
int x,y;
int calc(int kx,int ky){
return kx*x+ky*y;
}
Point operator + (const Point &B) const{
return {x+B.x,y+B.y};
}
}ed[N][N],dis[N],ans;
Point min(int kx,int ky,Point p1,Point p2){
return p1.calc(kx,ky)<p2.calc(kx,ky)?p1:p2;
}
Point prim(int kx,int ky){
Point res={0,0};
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
ed[i][j]={V,V};
}
}
for(int i=1;i<=m;i++){
int a=edge[i].a,b=edge[i].b,x=edge[i].x,y=edge[i].y;
ed[a][b]=min(kx,ky,ed[a][b],{x,y});
ed[b][a]=min(kx,ky,ed[b][a],{x,y});
}
memset(vis,0,sizeof(vis));
vis[1]=1;
dis[1]={V,V};
for(int i=2;i<=n;i++){
dis[i]=ed[1][i];
}
for(int i=2;i<=n;i++){
int p=1;
for(int j=2;j<=n;j++){
if(!vis[j]&&dis[j].calc(kx,ky)<dis[p].calc(kx,ky)){
p=j;
}
}
res=res+dis[p];
vis[p]=1;
for(int j=2;j<=n;j++){
dis[j]=min(kx,ky,dis[j],ed[p][j]);
}
}
return res;
}
void solve(Point A,Point B){
int kx=A.y-B.y,ky=B.x-A.x;
Point C=prim(kx,ky);
if(A.x<=C.x&&C.x<=B.x&&1ll*(C.y-A.y)*(C.x-B.x)>1ll*(C.y-B.y)*(C.x-A.x)){
if(1ll*ans.x*ans.y>1ll*C.x*C.y||(1ll*ans.x*ans.y==1ll*C.x*C.y&&ans.x>C.x)){
ans=C;
}
solve(A,C);
solve(C,B);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d%d",&edge[i].a,&edge[i].b,&edge[i].x,&edge[i].y);
edge[i].a++;
edge[i].b++;
}
Point A=prim(N*V,1),B=prim(1,N*V);
ans=A.x*A.y<B.x*B.y||(A.x*A.y==B.x*B.y&&A.x<B.x)?A:B;
solve(A,B);
printf("%d %d",ans.x,ans.y);
return 0;
}
-
其它解法
网上找到了一篇博客,没有细看,有兴趣的同学可以搜索“最小乘积生成树的另类做法”。
扩展
分治求凸壳,是为了维护最小乘积。最小乘积除了搭配最小生成树,还可以搭配很多其它的最优解问题,比如最短路,线性基,二分图最大/小权匹配,最大流最小割以及各种奇形怪状的 DP。
二维最小乘积背包例题:HDU5697 刷题计划 (2016"百度之星" - 初赛 Astar Round2B),注意卡常。
二维最小乘积匹配例题:P3236 [HNOI2014]画框。
三维最小乘积生成树
三维最小乘积:一种太不常见的套路。
问题
给出一个 \(n\) 个点 \(m\) 条边的无向图,第 \(i\) 条边有三个权值 \(a_i\),\(b_i\) 和 \(c_i\)。
求该图的一棵生成树 \(T\) ,使得 \(\left(\sum_{e\in T}a_e\right)\times\left(\sum_{e\in T}b_e\right)\times\left(\sum_{e\in T}c_e\right)\) 最小。
\(1 \leq n \leq 100,1 \leq m \leq 5000,0 \leq a_i,b_i,c_i \leq 255\),\(n,m,a_i,b_i,c_i\) 均为整数。
说句闲话
其实二维最小乘积要常见很多,三维最小乘积没有太大的必要,不过是二维凸包变成了三维凸包。
所以接下来关于三维最小乘积的都是三无内容:网上无任何题目,博客以及代码,并且我可能讲得有问题。
解法
-
一些尝试
问题和二维乘积最小生成树基本一样,能否套用之前的做法?
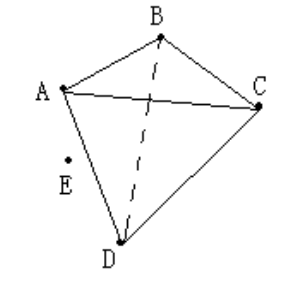
有个巨大的问题:分治法不管用了,因为这个方法求三维凸包会出错。
如下图,\(\{A,B,D\}\) 和 \(\{A,C,D\}\) 都会找到 \(E\) 点。
所以我们需要新的方法。
-
随机算法
这种问题一看就不好搞,所以为什么不尝试模拟退火呢?
考虑到最优方案在凸包上可能很突出,所以模拟退火的命中率非常高。
-
卷包裹法
不能用分治法求凸包是因为它本身会出错,所以我们考虑一种求三维凸包的靠谱方法:卷包裹法。
大概做法是开始时选择一条必定在凸包上的边,然后找到一个点使得其与这条边构成一个平面,且平面的一侧没有点,这样就找到了凸包的一个面,对这个面的另外两条边做相同的操作,直到没有新的点加入为止。
卷包裹法的复杂度为 \(\Omicron(nh)\)。
-
迭代法
不保证以下内容的正确性。
迭代法就是魔改版的卷包裹法,是论文作者自己想出来的,但是好像有一些问题。
-
具体流程
假设我们现在找到了面 \(ABC\),要找 \(D\) 点使得面 \(ABD\) 的一侧没有点,我们应该如何找到 \(D\) 点?
方法是对于面 \(ABC\) 找到最远的 \(C'\) 点,然后对于面 \(ABC'\) 找到最远的 \(C''\) 点,不停迭代即可找到 \(D\) 点。找最远点的过程依旧是推式子得到一个边权计算方式,然后求最小生成树。
-
边权转化
众所周知,向量可以解决 OI 中的一切几何问题。
有一种东西叫做向量的标量三重积,记作 \(\left[\vec{a},\vec{b},\vec{c}\right]\)。
\[\begin{aligned} \left[\vec{a},\vec{b},\vec{c}\right] &= \vec{a}\cdot(\vec{b}\times\vec{c})\\ &= (\vec{a}\times\vec{b})\cdot\vec{c}\\ &= \left| \begin{matrix} a_x&a_y&a_z\\ b_x&b_y&b_z\\ c_x&c_y&c_z\\ \end{matrix} \right| \\ \end{aligned} \]标量三重积的几何意义:三个向量定义的平行六面体,其体积等于三个向量的标量三重积的绝对值。
于是我们有一个式子:
\[V_{D-ABC} = \frac{1}{3}S_{\triangle{ABC}}h = \frac{1}{6}\left|\left[\vec{a},\vec{b},\vec{c}\right]\right| \]我们的目标是使面 \(ABC\) 上的高 \(h\) 最大,等价于 \(V_{D-ABC}\) 最大,类似于二维情况,我们可以用这个公式来转化最小生成树的边权。
-
复杂度证明
把所有点投影到以 \(\vec{AB}\) 为法向量的平面上,如下图。
设 \(D\) 点可能存在区域的面积为 \(S\),由于三种属性都是整数,所以当 \(S < 1\) 时停止迭代,当前找到的即为 \(D\) 点。
可以发现,每次迭代会使 \(S\) 至少减半,所以最多会进行 \(\Omicron(\log S)\) 次迭代。
对于时间复杂度的证明,上面这两句话似乎不够严谨,但考虑到极端情况极难构造(可以尝试一下有多难),复杂度大概率是可以接受的。欢迎大家给出严谨的证明或证伪。
迭代法找凸壳上一个点时间复杂度为 \(\Omicron(n^2\log{S}) = \Omicron(n^2(\log{n}+\log{V}))\),求三维最小乘积生成树的总时间复杂度为 \(\Omicron(n^2(\log{n}+\log{V})h)\)。
考虑到 EI 的结论,我们可以大胆推测求三维最小乘积生成树的总时间复杂度为 \(\Omicron(n^{\frac{11}{4}}V^{\frac{3}{4}}(\log{n}+\log{V}))\)。
-
-
求三维凸包的其它方法
-
增量法
复杂度爆炸,应该不行。
-
三维 QuickHull 法
注意二维和三维的 QuickHull 法完全是两个算法。
关于这个方法我没看懂,不知道可不可以魔改,如果行的话可能比迭代法更快。
大佬们可以提一提自己的想法,应该会有更好的做法(至少是有准确复杂度证明的做法)。
-
-
代码
由于没有提交地址,写了也不知道写对没有,所以我就不写了。当然代码并不难写,应该在 3k 以内,大家可以尝试。
扩展
同二位最小乘积一样,三维最小乘积也可以搭配各种最优解问题,然而目前在网上没有找到。
我们真的会碰到这种毒瘤题吗?
完结撒花
结束了。