电荷和场
关键方程
| 说明 |
方程 |
| Coulomb's law 库仑定律 |
\(\vec{\mathbf{F}}_{12} = \dfrac{1}{4\pi\varepsilon_0}\dfrac{q_1q_2}{r_{12}^2}\hat{\mathbf{r}}_{12}\) |
| 无限导线的电场 |
\(\vec{\mathbf{E}}(z)=\dfrac{1}{4\pi\varepsilon_0}\dfrac{2\lambda}{z}\hat{\mathbf{k}}\) |
| 无限平面的电场 |
\(\vec{\mathbf{E}}=\dfrac{\sigma}{2\varepsilon_0}\hat{\mathbf{k}}\) |
| 偶极矩 Dipole moment |
\(\vec{\mathbf{p}}=q\vec{\mathbf{d}}\) |
| 外部电场中偶极子上的扭矩 Torque |
\(\vec{\mathbf{\tau}}=\vec{\mathbf{p}}\times\vec{\mathbf{E}}\) |
电偶极子(Electric dipoles)
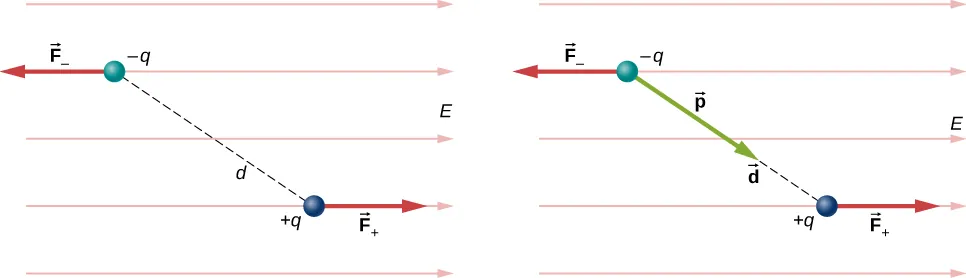
偶极矩 定义为: \(\vec{p} = q\vec{d}\),其中 \(q\) 为电荷量,\(\vec{d}\) 为电荷间距
外部电场中偶极子上的扭矩为: \(\vec{\tau} = \vec{p} \times \vec{E}\),其中 \(\vec{E}\) 为电场强度
电偶极子的电场为: \(\vec{E} = \dfrac{-1}{4\pi\varepsilon_0}\left(\dfrac{\vec{p}}{r^3}\right)\)
高斯定律
关键方程
| 说明 |
方程 |
| 均匀电场的电通量 flux |
\(\Phi = \vec{\mathbf{E}}\cdot\vec{\mathbf{A}}\) |
| 通过开放曲面的电通量 |
\(\Phi = \displaystyle\int_{S} \vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA = \displaystyle\int_{S} \vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}\) |
| 通过封闭曲面的电通量 |
\(\Phi = \displaystyle\oint_{S} \vec{\mathbf{E}}\cdot\hat{\mathbf{n}}dA = \displaystyle\oint_{S} \vec{\mathbf{E}}\cdot d\vec{\mathbf{A}}\) |
| 高斯定律 |
\(\displaystyle\oint_{S} \vec{\mathbf{E}}\cdot \hat{\mathbf{n}}dA = \dfrac{q_{enc}}{\varepsilon_0}\) |
| 导体表面外的电场 |
\(E = \dfrac{\sigma}{\varepsilon_0}\) |
电势
关键方程
| 说明 |
方程 |
| 双电荷系统的势能 |
\(\displaystyle U(r) = k\dfrac{q_1q_2}{r}\) |
| 电势差 |
\(\Delta V = \dfrac{\Delta U}{q}\) |
| 电势 |
\(\displaystyle V=\dfrac{U}{q} = -\int_{R}^{P} \vec{\mathbf{E}}\cdot d\vec{\mathbf{l}}\) |
| 两点之间的电势差 |
\(\displaystyle V_{BA} = -\int_{A}^{B} \vec{\mathbf{E}}\cdot d\vec{\mathbf{l}} = V_B - V_A\) |
| 点电荷的电势 |
\(\displaystyle V = \dfrac{1}{4\pi\varepsilon_0}\dfrac{q}{r} = \dfrac{kq}{r}\) |
| 电偶极矩 |
\(\vec{\mathbf{p}}=q\vec{\mathbf{d}}\) |
| 电偶极子的电势 |
\(\displaystyle V = \dfrac{1}{4\pi\varepsilon_0}\dfrac{\vec{\mathbf{p}}\cdot\hat{\mathbf{r}}}{r^2}\) = \(k\dfrac{\vec{\mathbf{p}}\cdot\hat{\mathbf{r}}}{r^2}\) |
| 连续电荷分布的电势 |
\(\displaystyle V_P = \dfrac{1}{4\pi\varepsilon_0}\displaystyle\int \dfrac{dq}{r} = k\displaystyle\int \dfrac{dq}{r}\) |
| 电场作为电势梯度 |
\(\vec{\mathbf{E}} = -\vec{\mathbf{\nabla}}V\) |
| 笛卡尔坐标中的 Nabla 算子 |
\(\vec{\mathbf{\nabla}} = \hat{\mathbf{i}}\dfrac{\partial}{\partial x} + \hat{\mathbf{j}}\dfrac{\partial}{\partial y} + \hat{\mathbf{k}}\dfrac{\partial}{\partial z}\) |
| 柱坐标中的 Nabla 算子 |
\(\vec{\mathbf{\nabla}} = \hat{\mathbf{r}}\dfrac{\partial}{\partial r} + \hat{\mathbf{\theta}}\dfrac{1}{r}\dfrac{\partial}{\partial \theta} + \hat{\mathbf{z}}\dfrac{\partial}{\partial z}\) |
| 球坐标中的 Nabla 算子 |
\(\vec{\mathbf{\nabla}} = \hat{\mathbf{r}}\dfrac{\partial}{\partial r} + \hat{\mathbf{\theta}}\dfrac{1}{r}\dfrac{\partial}{\partial \theta} + \hat{\mathbf{\varphi}}\dfrac{1}{r\sin\theta}\dfrac{\partial}{\partial \varphi}\) |
电容
关键方程
| 说明 |
方程 |
| 电容 Capacitance |
\(\displaystyle C = \dfrac{Q}{V}\) |
| 平行板电容器(parallel-plate capacitor)的电容 |
\(\displaystyle C = \dfrac{\sigma A}{Ed} = \varepsilon_0\dfrac{ A}{d}\) |
| 真空球形电容器(vacuum spherical capacitor)的电容 |
\(\displaystyle C = 4\pi\varepsilon_0\dfrac{R_1R_2}{R_2-R_1}\) |
| 真空圆柱体电容器(vacuum cylindrical capacitor)的电容 |
\(\displaystyle C = 2\pi\varepsilon_0\dfrac{l}{\ln\dfrac{R_2}{R_1}}\) |
| 串联电容器的电容 |
\(\displaystyle \dfrac{1}{C} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \cdots + \dfrac{1}{C_n}\) |
| 并联电容器的电容 |
\(\displaystyle C = C_1 + C_2 + \cdots + C_n\) |
| 能量密度 |
\(\displaystyle u_E = \dfrac{1}{2}\varepsilon_0E^2\) |
| 电容器的能量 |
\(\displaystyle U_C = \dfrac{1}{2}CV^2 = \dfrac{1}{2}QV = \dfrac{1}{2}Q^2C\) |
| 带电介质的电容器电容 |
\(\displaystyle C = \kappa C_0\) |
| 带电介质的电容器能量 |
\(\displaystyle U = \dfrac{1}{\kappa}U_0\) |
| 介电常数 Dielectric constant |
\(\displaystyle \kappa = \dfrac{E_0}{E}\) |
| 电介质中的感应电场 |
\(\displaystyle \vec{\mathbf{E}}_i=(\dfrac{1}{\kappa}-1)\vec{\mathbf{E}}_0\) |
电流和电阻
关键方程
| 说明 |
方程 |
| 电流 |
\(\displaystyle I = \dfrac{dQ}{dt}\) |
| 漂移速度 drift velocity |
\(\displaystyle v_d = \dfrac{I}{nqA}\) |
| 电流密度 |
\(\displaystyle I = \iint \vec{\mathbf{J}}\cdot d\vec{\mathbf{A}}\) |
| 电阻率 resistivity |
\(\displaystyle \rho = \dfrac{E}{J} = \dfrac{E}{\sigma E} = \dfrac{1}{\sigma}\) |
| 电阻率和温度的关系 |
\(\displaystyle \rho = \rho_0[1+\alpha(T-T_0)]\) |
| 电阻 |
\(\displaystyle R = \rho \dfrac{L}{A} \equiv \dfrac{V}{I}\) |
直流电路
关键方程
|路端电压|\(\displaystyle V_{terminal} = \varepsilon - Ir\)|
