\(\mathcal{Description}\)
给你一棵有 \(n\) 个结点的树,定义 \(G_k\)为将在原树中所有距离大于等于 \(k\) 的点对间连一条无向边所构成的无向图(距离定义为简单路径中边的数量)。
对于所有 \(1 \le k \le n\),求 \(G_k\) 中连通块的数量。
\(2\le n\le 10^5\)
\(\mathcal{Solution}\)
设树的直径为\(d\),对于\(k > d\)的情况,\(G_k\)中没有边,连通块的数量为\(n\)
以下是我的思考过程,逐渐从比较麻烦的想法变得简单
可以先看正解,没看懂再回来看
考虑\(k\)从大变小的过程,之前连了的边\(k\)变小后也会连,因此可以考虑每次增加的新点
这时候想到了直径,假设整棵树只有一条直径,\(k=d\)时,只有直径的两个端点是连在一起的,考虑\(k\)变小的过程,因为任意一个点到其它点最远的距离就是到这条直径的某个端点,最开始两个端点连了边,当\(k\)变小\(i\),可以认为从直径的一个端点出发最多走\(i\)步,所到达的这些点都会和直径的另一个端点连起来
如图,两个直径端点在\(k\)变小的过程会不断新增另一端点附近的点

这样的过程可以用\(bfs\)模拟出来,目前这种做法仍然有问题,一是树并不是只有一条直径,对于多条直径其实也可以用\(dfs\)找出来然后再\(bfs\)模拟,二是比较关键的问题,如下的情况并没有被正确考虑到
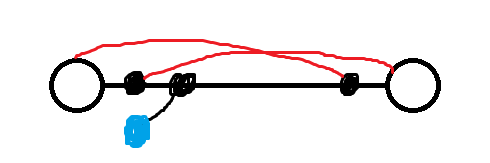
蓝色的点对于左端点而言要走三步下才能到达,而对右端点而言,它们的距离为\(d-1\),应该早就被连边,而在我们的\(bfs\)模拟的方法中,并没能正确的连接到
以下是正解部分
现在让我们舍弃掉\(bfs\)这个愚蠢的方法,首先重新捋一下几个性质
- 所有直径端点在\(k=d\)时都会连边进同一个连通分量
- 除了和直径端点在同一个连通分量里的点,其它点都是独立的大小为1连通分量
- 离直径端点距离为\(i\)的点,在\(k=i\)时会和直径端点连边
根据以上性质,我们可以发现我们需要求出的东西是,每个点到所有直径端点的距离中最远距离\(dm\),这个点会在\(k=dm\)时,进入直径端点所在连通分量,也就是连通分量数会减少\(1\),令\(i=d-dm\),也就是当\(k\)从\(d\)开始减少\(i\)时联通分量数会减少\(1\)
现在问题就变成了有若干个点(直径端点),求每个点到这些点最远的距离
因为是直径端点,因此会有一些性质让问题变得好求,首先如果有多个直径,并且这些直径的端点没有相同的点时,这两些直径的交点一定是在距离某个直径端点\(d/2\)的位置
若直径为偶数,我们把这个树从直径中间的位置提起来
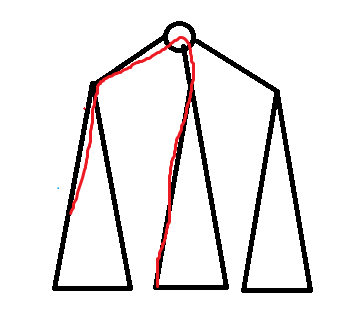
这时,这棵树的深度不会超过\(d/2\),任意一点都可越过根节点走到某一个直径端点,也就是说任意一点到某个直径端点的最长距离为\(\frac{d}{2}+dep-1\),对应的\(i=\frac{d}{2}-dep+1\)
而对于直径为奇数的情况
我们也找到中间位置
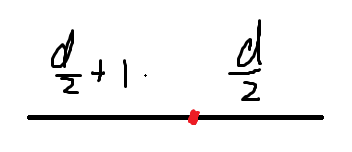
先考虑右边这部分,将红色的点提出来作为根节点,这时只考虑右边这部分点,不考虑左边的点,这些点可以越过根节点然后走到某一个离红色点长度为\(\frac{d}{2}+1\)的直径端点,也就是说最长距离为距离为\(\frac{d}{2}+dep\),对应的\(i=\frac{d}{2}-dep+1\)
而对于左边这部分,我们只需把红色的点往左移一次,就能变成相同的情况了
我们发现直径为奇数和偶数的情况得到的\(i\)的计算式子是一样的,因此可以共用同一个\(dfs\)解决
现在只剩下一个简单的问题,如何找到直径的中点,这个问题应该有很多种解决办法,我是使用记录儿子中最深和次深的点是谁来求直径,并记录找到直径的结点,顺便用\(s[i]\)表示以\(i\)为根节点的子树到最深的点应该往\(i\)的哪个儿子走,这样只需从之前记录的结点开始每次都往\(s[i]\)的方向走,直到找到最深和次深的深度相同或者相差一就找到了一条直径的中点了
所有的点的\(i\)都得到了,之后我们就可以直接计算在\(k=d-i\)时会减少多少个连通分量了,问题就解决了
\(\mathcal{Code}\)
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 200005;
int n, cnt, d, g;
int head[maxn], nxt[maxn], to[maxn];
int mx1[maxn], mx2[maxn], dep[maxn], s1[maxn];
int ans[maxn], need[maxn];
queue <int> q;
void add (int u, int v)
{
nxt[++cnt] = head[u], head[u] = cnt, to[cnt] = v;
}
void dfs1 (int u, int father)
{
dep[u] = dep[father] + 1;
mx1[u] = mx2[u] = u;
for (int e = head[u]; e; e = nxt[e])
if (to[e] != father) {
dfs1(to[e], u);
if (dep[mx1[to[e]]] > dep[mx2[u]]) mx2[u] = mx1[to[e]];
if (dep[mx2[u]] > dep[mx1[u]]) swap(mx1[u], mx2[u]);
if (mx1[to[e]] == mx1[u]) s1[u] = to[e];
}
int dis = dep[mx1[u]] + dep[mx2[u]] - 2 * dep[u];
if (dis > d) {
d = dis;
g = u;
}
}
void dfs2 (int u, int father)
{
dep[u] = dep[father] + 1;
need[u] = min(need[u], d / 2 - (dep[u] - 1));
for (int e = head[u]; e; e = nxt[e])
if (to[e] != father) dfs2(to[e], u);
}
int main ()
{
scanf("%d", &n);
for (int i = 2, u, v; i <= n; ++i) {
scanf("%d%d", &u, &v);
add(u, v), add(v, u);
}
for (int i = 1; i <= n; ++i) need[i] = n;
dfs1(1, 0);
for (int i = n; i > d; --i) ans[i] = n;
if (d & 1) {
while (dep[mx1[g]] - dep[g] != d / 2 + 1) g = s1[g];
dep[s1[g]] = 0;
dfs2(g, s1[g]);
dep[g] = 0;
dfs2(s1[g], g);
}
else {
while (dep[mx1[g]] - dep[g] != d / 2) g = s1[g];
dfs2(g, 0);
}
for (int i = 1; i <= n; ++i) --ans[d - need[i]];
++ans[d];
for (int i = d; i; --i) ans[i] += ans[i + 1];
for (int i = 1; i <= n; ++i) printf("%d%c", ans[i], " \n"[i == n]);
return 0;
}
如有哪里讲得不是很明白或是有错误,欢迎指正
如您喜欢的话不妨点个赞收藏一下吧