Grandient Descent

1. 梯度下降法

1.1 梯度与梯度下降

对于 一元函数 来说，梯度就是函数的导数；对于 多元函数 来说，梯度是一个由函数所有 偏微分 组成的向量。

梯度下降 是通过一步步迭代，使得所有 偏微分 的值达到最低。

可以以简单的 一元二次函数 \(y = (x - 1)^2\) 为例：

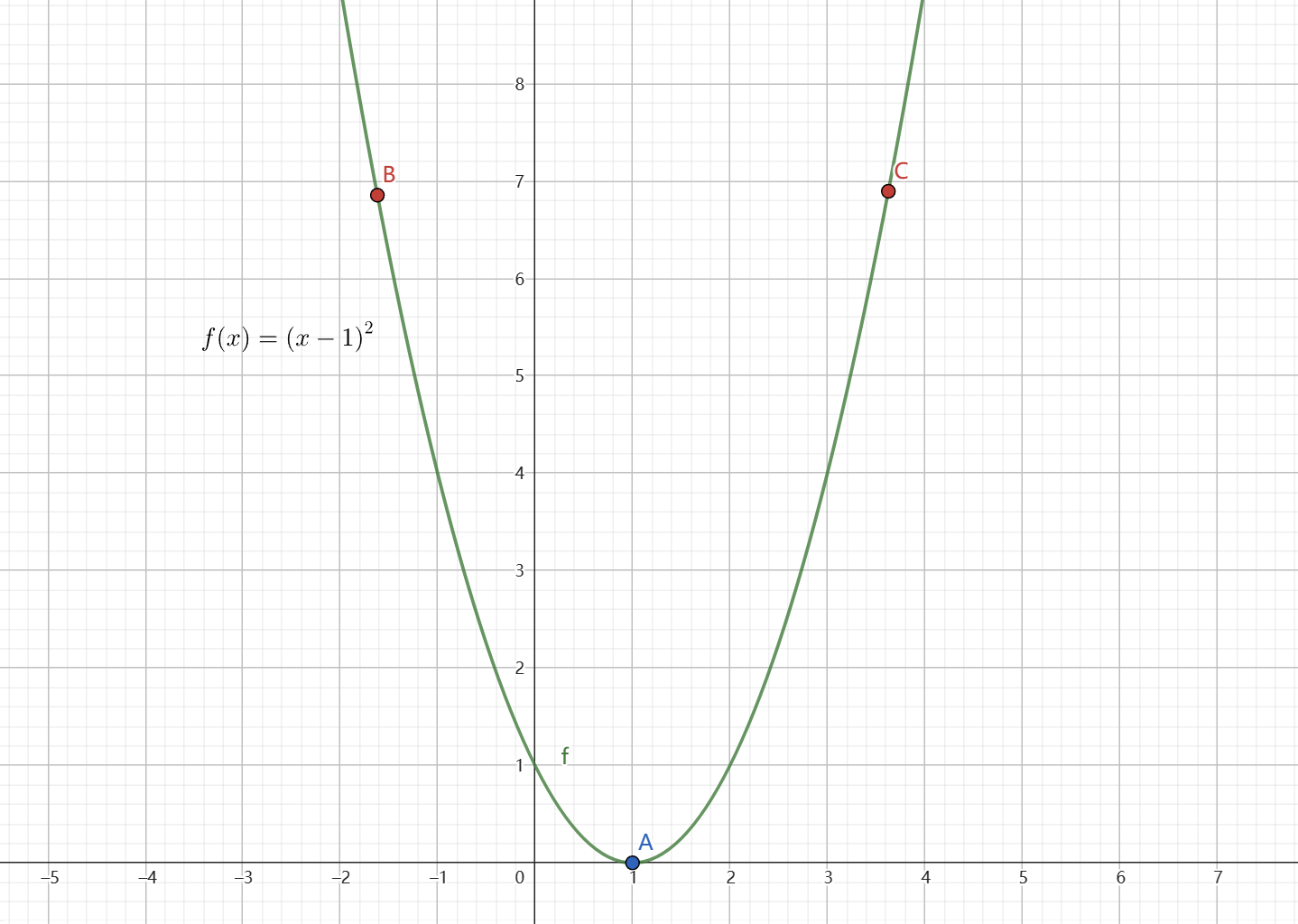
其中 \(\text{A}\) 点为函数的最低点，\(\text{B}\) 点和 \(\text{C}\) 点位于其左右两边。

\(\text{A}\) 点所在之处的 \(x\) 为 1，显然当 \(x < 1\) 时，函数图像沿 右下方 延伸，此时 导数符号 为负；反之，\(x > 1\) 时，函数图像沿 左下方 延伸，此时 导数符号 为正。

根据图像，对于 \(\text{B}\) 点，为了达到最低点（即函数达到最小值），\(x\) 需要向右移动，即增大 \(x\)；对于 \(\text{C}\) 点来说，则 \(x\) 需要向左移动，即减小 \(x\)。

根据 导数的符号 以及 \(x\) 的移动方向，可以看出 \(x\) 的 移动方向 由 导数的符号 决定，只要 \(x\) 沿着导数（梯度）相反的方向不断移动，就可以达到最小值点。这也是 梯度下降法 的真正含义。

由此有 \(x\) 的更新表达式：

\[x := x - \eta \frac{\text{d}}{\text{d}x}f(x) \]

其中，\(\eta\) 成为 学习率，不同的 学习率的取值 ，达到最小值的 迭代次数 也会随之产生变化。也就是收敛速度不同。

1.2 梯度下降法求解一元线性回归

上面讲了 梯度下降法，我们再回顾一下 一元线性回归问题 中的 损失函数 \(E\)（最小二乘法），即：

\[E = \frac{1}{2}\sum_{i=1}^{n}(y_i - f_{\theta}(x_i))^2 \]

一元线性回归 的最终目标是为了 最小化损失函数的值 来得到最优参数 \(\theta\) 。显然，我们可以用 梯度下降法 来实现 损失函数的最小化。

对于一元线性回归问题， \(\theta_1\) 和 \(\theta_0\) 是 损失函数的参数，由 梯度下降 可以得到 参数的更新表达式:

\[\begin{split} \theta_0 := \theta_0 - \eta \frac{\partial E}{\partial \theta_0} \\\\ \theta_1 := \theta_1 - \eta \frac{\partial E}{\partial \theta_1} \end{split} \]

对于上述更新表达式中的 偏微分，我们可以 阶梯性 地进行微分：

\[\frac{\partial E}{\partial \theta} = \frac{\partial E}{\partial(y - f_\theta(x))} \frac{\partial(y - f_\theta(x))}{\partial \theta} \]

将两个部分分开求解:

\[\begin{align*} \frac{\partial E}{\partial(y - f_\theta(x))} & = \frac{\partial}{\partial(y - f_\theta(x))}(\frac{1}{2}\sum_{i=1}^{n}(y_i - f_{\theta}(x_i))^2) \\\\ & = \frac{1}{2}\sum_{i=1}^n(\frac{\partial}{\partial(y_i - f_\theta(x_i))}(y_i - f_{\theta}(x_i))^2) \\\\ & = \sum_{i=1}^n (y_i - f_{\theta}(x_i)) \\\\\\ \frac{\partial (y - f_{\theta}(x))}{\partial \theta_0} & = -1 \\\\\\ \frac{\partial (y - f_{\theta}(x))}{\partial \theta_1} & = -x \end{align*} \]

由上述推导，可以得到：

\[\begin{split} & \frac{\partial E}{\partial \theta_0} = \sum_{i=1}^n (f_{\theta}(x_i) - y_i) \\\\ & \frac{\partial E}{\partial \theta_1} = \sum_{i=1}^n (f_{\theta}(x_i) - y_i)x_i \end{split} \]

由此，具体的 更新表达式 如下：

\[\begin{split} & \theta_0 := \theta_0 - \eta \sum_{i=1}^n (f_{\theta}(x_i) - y_i) \\\\ & \theta_1 := \theta_1 - \eta \sum_{i=1}^n (f_{\theta}(x_i) - y_i)x_i \end{split} \]

经过不断的迭代，最终使得 损失函数最小化，得到 最优参数，从而实现拟合。至此，完成了 梯度下降法求解一元线性回归。

1.3 梯度下降法求解多元线性回归

在 多元线性回归问题 中，我们可以向量化表示 \(y = \theta_0 + \theta_1 x_1 + \cdots + \theta_d x_d\):

\[y = X\theta \]

其中

\[y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} \qquad X = \begin{bmatrix} 1 & x_{11} & \cdots & x_{1d} \\ 1 & x_{21} & \cdots & x_{2d} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{nd} \end{bmatrix} \qquad \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_d \end{bmatrix} \]

由此 损失函数的向量化表示 如下：

\[E = \frac{1}{2}(y - X\theta)^T(y - X\theta) \]

将 \(E\) 对 \(\theta\) 求偏微分（这里写了两种求法）：

阶梯型求偏微分

\[\frac{\partial E}{\partial \theta} = \frac{\partial E}{\partial (y - X\theta)} \frac{\partial(y - X\theta)}{\partial \theta} = (y - X\theta)(- X^T) = X^T(X\theta - y) \]

传统方法求偏微分

\[\begin{split} E & = \frac{1}{2}(y - X\theta)^T(y - X\theta) \\\\ & = \frac{1}{2}(y^T - \theta^TX^T)(y - X\theta) \\\\ & = \frac{1}{2}(y^Ty - \theta^TX^Ty - y^TX\theta + \theta^TX^TX\theta) \\\\\\ \frac{\partial E}{\partial \theta} & = \frac{1}{2}(- X^Ty - (y^TX)^T + 2X^TX\theta) \\\\ & = X^T(X\theta - y) \end{split} \]

由此可以得到 梯度下降法 求解 多元线性回归问题 的参数 更新表达式:

\[\theta := \theta - \eta X^T(X\theta - y) \]

通过不断迭代，最终得到最优参数 \(\theta\)，完成 梯度下降法求解多元线性回归。

1.4 学习率

学习率（learning rate）的取值一直都是比较玄学的， 既不能过大，也不能过小 。学习率决定了每一次迭代过程中参数变化的步长。当 学习率过大 ，参数变化的跨度过大，极有可能会导致无法达到收敛状态，甚至出现 发散、震荡；当 学习率过小，参数变化太慢，会导致 迭代次数过多，以至于短时间内无法达到收敛状态。

所以需要不断选取学习率进行一步步的调试，直到达到比较理想的收敛状态。对于比较复杂的问题，尤其涉及多维度变量时，学习率的取值应当从较小的值开始，例如0.05、0.1等。如果 loss 变化很小，或者达到收敛状态的速度很慢，此时可以逐步一点点提高学习率，直到达到最佳的曲线。但取值一定不能过大，对于一个问题一般学习率有个上限，当超过这个限度之后就有可能出现无法收敛的结果了。

2. 梯度下降法核心代码

import numpy as np
from sklearn import datasets

X, Y = ...
alpha = ... # 学习率
theta = ... # 参数
t = ... # 迭代次数

# 函数
def f(X, theta):
    return X @ theta

# 损失函数
def E(X, Y, theta):
    return np.sum(np.dot((np.dot(X, theta) - Y).T, (np.dot(X, theta) - Y))) / (2 * len(X))

# 梯度下降
def gradientDescent(X, Y, theta, alpha, t):
    costs = []
    for _ in range(t):
        theta -= np.dot(X.T, (np.dot(X, theta) - Y)) * alpha / len(X)
        costs.append(E(X, Y, theta))
    return theta, costs

# 预测
theta, costs = gradientDescent(X, Y, theta, alpha[0], t[2])
pred_y = f(X, theta)