概
一般的位置编码建模的是序列信息而不是绝对的时间信息, 本文介绍一种可以引入时间间隔信息的位置编码.
Motivation
-
一般的 attention 机制如下所示:
\[\text{Attn}(\mathbf{Q, K, V}) = \text{softmax}(\frac{\mathbf{QK}^T}{\sqrt{d}}) \mathbf{V}, \]但是就注意力机制本身而言, 是不具备序列先后关系区分的能力的. 故而, 像 transformer 之类会在最开始的 embedding 部分加入位置编码:
\[Z + P. \] -
不过, 一般的 \(P\) 能够区分序列的位置, 即先后关系, 但是无法告知你对应的具体的时间 \(t \in T[0, t_{\text{max}}]\), 但是有些时候, 具体的时间 \(t\) 也是十分重要的.
-
作者希望找到一个映射 \(\Phi: T \rightarrow \mathbb{R}^d\), 然后通过:
\[Z \| \Phi(t) \]来注入时间信息.
-
更为具体一点, 作者不希望直接建模绝对的时间戳 (或许出于泛化性的考虑), 而是希望注入时间间隔的信息, 注意到:
\[[Z_1\|\Phi(t_1)]' [Z_2 \| \Phi(t_2)] = \langle Z_1, Z_2 \rangle + \langle \Phi(t_1), \Phi(t_2) \rangle. \] -
看到 \(\Phi\) 和 \(\langle \cdot, \cdot \rangle\), 我们很容易想到 RKHS, 即我们可以直接建模:
\[\mathcal{K}(t_1, t_2) := \langle \Phi(t_1), \Phi(t_2) \rangle, \]倘若 kernel \(\mathcal{K}(t_1, t_2) = \psi (t_1 -t_2)\), 则此 kernel 是 time-invariant 的, 这是很有用的性质.
-
不过, 作者引入 \(\mathcal{K}\) 并不是希望真的去构建这样一个 kernel, 而是探讨在这种 time-invariant 的情况下, 具体的 \(\Phi\) 具有怎样的形式.
Bochner
-
首先我们有如下的定理:
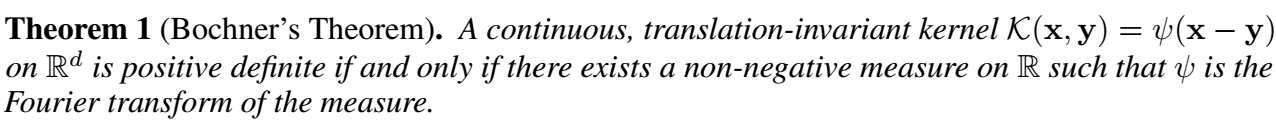
-
即, 为了保证 \(\mathcal{K}\) 是对称半正定的, 我们需要满足存在非负的测度 \(p\):
\[\tag{2} \mathcal{K}(t_1, t_2) = \psi (t_1, t_2) =\int_{\mathbb{R}} e^{iw(t_1 - t_2)} p(\omega) d\omega = E_{\omega}[\xi_{\omega}(t_1) \xi_{\omega}(t_2)^*], \: \xi_{\omega}(t) := e^{i\omega t}. \] -
既然 \(\mathcal{K}, p(\omega)\) 都是实的, 我们可以得到:
\[\mathcal{K}(t_1, t_2) = E_{\omega}[\cos(\omega (t_1 - t_2))] = E_{\omega}[\cos(\omega t_1)\cos(\omega t_2) + \sin(\omega t_1) \sin (\omega t_2)]. \] -
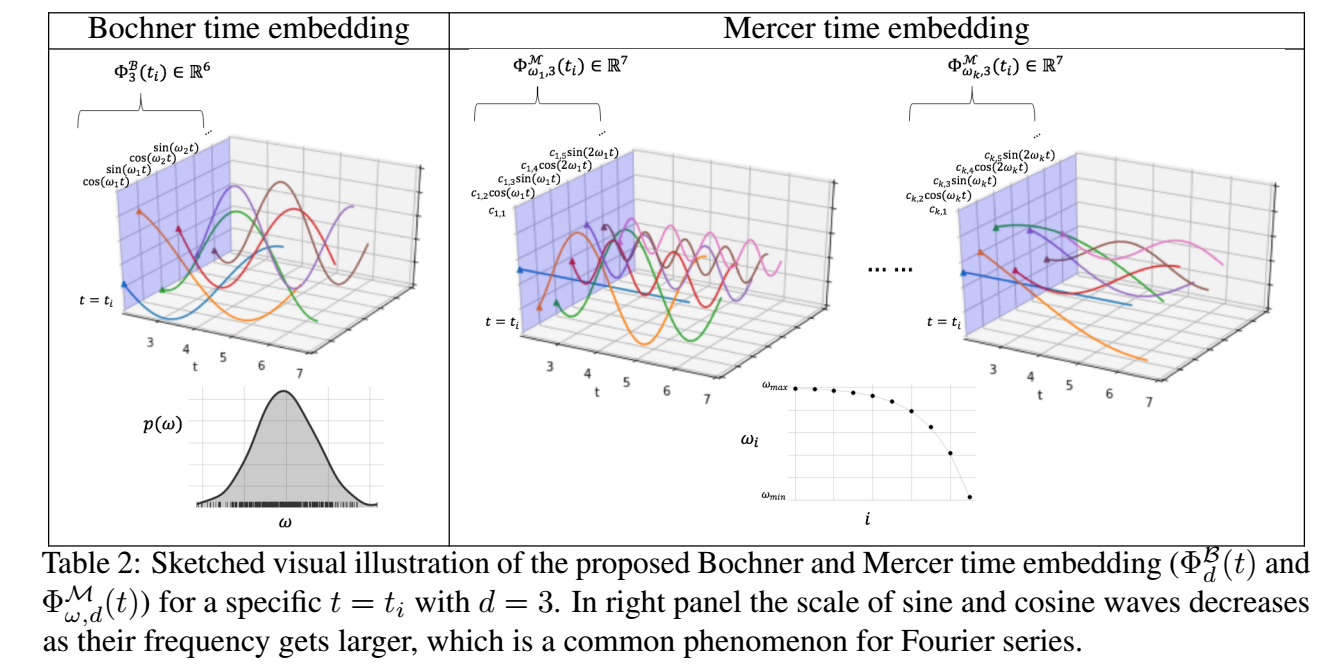
倘若我们能够从 \(p(\omega)\) 中采样 \([\omega_1, \ldots, \omega_d]\), 则 \(\mathcal{K}(t_1, t_2)\) 可以近似为:
\[\frac{1}{d} \sum_{i=1}^d [\cos (\omega_i t_1) \cos(\omega_i t_2) + \sin (w_i t_1) \sin (\omega_i t_2)] = \Phi_d^{\mathcal{B}}(t)' \Phi_d^{\mathcal{B}}(t), \]其中
\[\Phi_d^{\mathcal{B}}(t) := \sqrt{\frac{1}{d}} [\cos(\omega_1t), \sin(\omega_1t), \ldots, \cos(\omega_d t), \sin (\omega_d t)]. \] -
现在, 我们需要解决的问题是 \(p(\omega)\) 的采样问题. 实际上, 可以这么认为, 给定任意的非负测度 \(p(\omega)\), 都能确定一种 \(\mathcal{K}\), 所以作者选择训练 \(p_{\theta}(\omega)\):
-
一种方式是令其为高斯分布:
\[p_{\theta}(\omega) = \mathcal{N}(\omega; \theta = \{\mu, \sigma\}), \]采样只需通过:
\[\mu + \sigma \odot \epsilon, \quad \epsilon \sim \mathcal{N}(0, I). \] -
第二种方式是, 倘若随机变量 \(X\) 具有概率分布函数 \(P(X < x) = F(x)\), 则
\[F^{-1}(U) = X, \]其中 \(U\) 表示均匀分布. 于是, 我们可以建模 \(F^{-1} := g_{\theta}\) (通过 normalizing flow), 然后
\[\omega = g_{\theta}(\epsilon), \epsilon \sim \mathcal{U}[0, 1] \]即可.
-

- 注: 如果我没理解错误的话, 上面提到的 \(\theta\) 是在一般的损失函数的监督下训练的.
Mercer
-
我们可以从 Mercer' Theorem 中获得更直接的启发:

-
它启发我们可以直接构建:
\[\Phi^{\mathcal{M}}(t) := [\sqrt{c_1}\phi_1(t), \sqrt{c_2}\phi_2 (t), \ldots]. \] -
当然, \(\phi\) 本身如何确定是一个问题. 当 \(\psi(t_1 - t_2)\) 是一个周期性函数的时候, 有如下性质:

-
此时
\[\Phi^{\mathcal{M}}(t) := [\sqrt{c_1}, \sqrt{c_2} \cos(\frac{j\pi t}{\omega}), \sqrt{c_{2j + 1}} \sin(\frac{j\pi t}{\omega}), \ldots], \]其中 \(c_j\) 为傅里叶系数. 由于傅里叶系数随着 \(j\) 增大逐渐减小, 所以我们实际上可以选择前面的部分进行近似.
-
当然, 周期性的假设可能过于强烈了, 此时我们可以选择多个 \(\omega_1, \omega_2, \ldots, \omega_k\). 作者令:
\[\omega_i = \omega_{max} - (\omega_{max} - \omega_{min})^{i / k}, \: i=1,\ldots, k, \]其中 \([\omega_{min}, \omega_{max}]\) 是认为设定的频率的范围.
代码
[official]
- Self-attention Representation Functional attention Learningself-attention representation functional attention self-attention self-attention attention self recommendation self-attention sequential stochastic self-attention local-global interactions transformers self-attention attention笔记self self-attention attention self 4.1 self-attention注意力attention机制 attention self-attention multi-head multi self-attention modifications predicting expression