$$dfs$$

深度优先搜索，全称 Depth First Search，通常有两种意义：递归暴力枚举每种情况、图论中用于遍历或搜索图的算法。

搜索：递归暴力枚举每种情况

OI-wiki Link

没有什么好说的，经常用于打暴力，像 xhr 神仙就可以用它打出 HN 2023 小学组 S 1=。

洛谷 P2089 烤鸡

给定一个整数 \(n\)，你现在要确定 \(10\) 个变量 \(x_1,x_2\cdots x_{10}\) 的值，满足 \(\sum\limits_{1\leqslant i \leqslant 10} x_i = n\) 且对于每个 \(1\leqslant i \leqslant 10\)，\(1\leqslant x_i \leqslant 3\)，输出方案数和每种方案。

要枚举 \(10\) 个变量的值，你当然可以写 \(10\) 重循环枚举，可如果他要求你枚举 \(m\) 个变量的值呢？这时，你就需要用递归来处理。

对于每层递归，枚举每种情况，然后进入下一层递归。当递归枚举完每个数的情况后，判断情况是否满足要求，然后返回上一层递归。

#include <bits/stdc++.h>

using namespace std;

int n, a[15], ans;
vector<vector<int>> v;

void dfs (int x) {
  if (x == 11) {
    vector<int> t;
    int sum = 0;
    for (int i = 1; i <= 10; i++) {
      sum += a[i], t.push_back(a[i]);
    }
    if (sum == n) {
      ans++, v.push_back(t);
    }
    return ;
  }
  a[x] = 1, dfs(x + 1);
  a[x] = 2, dfs(x + 1);
  a[x] = 3, dfs(x + 1);
}

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  dfs(1);
  cout << ans << '\n';
  for (auto i : v) {
    for (int j : i) {
      cout << j << ' ';
    }
    cout << '\n';
  }
  return 0;
}

图论：用于遍历或搜索图的算法

OI-wiki Link

没啥好说的。

$$bfs$$

OI-wiki Link

广度优先搜索，没啥好说的。

双向广搜

顾名思义，就是从起点和终点同时开始进行广搜，当两边都找到同一点时直接更新。

剪枝

剪枝，用于优化搜索的效率。

最优性剪枝

如果当前状态无论如何也不可能对答案造成影响，直接 return ; 即可。

可行性剪枝

若当前状态已经不符合要求，直接 return ; 即可。

$$\texttt{A}^*$$

\(A^*\) 搜索算法，简称 \(A^*\)(A-star)，是一种在图形平面上，对于有多个节点的路径求出最低通过成本的算法，属于图的遍历+最佳优先搜索，也是 BFS 的改进。

过程

首先给出起点和终点，定义从起点开始的距离函数 \(f(x)\) 和距离终点的估价函数 \(g(x)\)，那么整体的估价函数就是 \(c(x)=f(x)+g(x)\)。

为了尽量让答案更优，肯定优先选择 \(c(x)\) 最小的元素，这个明显可以用优先队列维护，每次取出队头，然后更新相邻元素状态。

整体来看，\(A^*\) 属于 BFS 的改良版且改良之后形态类似 dijkstra。

$$\texttt{IDDFS}$$

迭代加深搜索 IDDFS，是一种每次限制搜索深度的 DFS，本质还是深搜，但每次搜索前首先规定一个最大深度 \(d\)，搜索时深度不能超过 \(d\)，一般用于寻找最优解。如果在当前深度下没有找到答案就将 \(d\) 加 \(1\)，继续搜索。

对比

同是找最优解，为啥不用 BFS 呢？

因为 BFS 需要使用队列，而队列复杂度不低，空间消耗也会比较大，当状态数多了之后 BFS 的劣势也就显出来了。

迭代加深搜索本质为深搜，空间耗费相对较小，而且当搜索树分叉较多时，每增加一次深度搜索的复杂度都会出现指数级增长，那么重复搜索所带来的消耗几乎可以不记，所以它时间复杂度是可以近似看成 BFS 的。

过程

初始时规定一个深度 \(d\)(设为一个极小值)，每次搜索的深度不能超过 \(d\)，超过了就返回。

在当前深度内寻找目标状态，如果找到了就回溯，退出外层的深度规定；否则将 \(d\) 加一，继续找。

srds，在大部分题目里 BFS 还是方便些的，因为它很容易判重。

但如果空间比较极限，再加上找最优解的话，还是可以考虑使用 IDDFS 的。

$$\texttt{IDA}^*$$

顾名思义，\(IDA^*\) 就是迭代加深搜索+\(A^*\)，通过限制深度来减少一定情况下的复杂度，优点：

• 不需要判重，不需要排序，利于深度剪枝。
• 空间需求减少：每个深度下实际上是一个深度优先搜索，不过深度有限制，使用 DFS 可以减小空间消耗。

缺点：

• 重复搜索了一部分。

OI-wiki Link

引入

动态规划(Dynamic Programming，DP)，是一种将原问题分为一些子问题，通过局部最优解推出全局最优解。

一般来说，做一道 dp 题有 \(4\) 个步骤：

1. 设计 dp 状态：根据几个关键信息定下状态和最优化属性。
2. 定下拓扑序。
3. 设计状态转移方程。
4. 确定初始状态、目标状态和边界条件。

基本要求

dp 的基本要求有三个：

• 最优子结构性质：即你需要保证当前状态的最优结果都是由子问题的最优结果转移而来。
• 无后效性：即当前的选择在你的状态设计下不会影响后续的决策。
• 子问题重叠：当有大量子问题时，需要把这些子问题的结果记录下来，防止多次求解导致效率低下。

dp 的分类

大致可分为如下几类：

• 序列 dp
• 背包 dp
• 区间 dp
• DAG 上 dp
• 树形 dp
• 状压 dp
• 概率 dp
• 还有些不会的，见 OI-wiki。

其中序列、背包、区间、概率 dp 都是线性 dp。

还有一些其他类型的 dp，比较有意思。

线性 dp

线性DP是动态规划问题中的一类问题，指状态之间有线性关系的动态规划问题。

虽然是线性 dp，但部分时间复杂度并不是纯线性的，因为线性 dp 的时间复杂度并不一定是线性的。

其他类型 dp：P1216 数字三角形

如果只是单纯的去考虑走最大数，你就会陷入坑中，考虑动态规划。

不要去看原图，只用看读入的数据，这样不抽象。

令 \(a_{i,j}\) 表示第 \(i\) 行第 \(j\) 个数，那么从 \((i,j)\) 就可以移动到 \((i+1,j)\) 或 \((i+1,j+1)\)。

• 状态：\(dp_{i,j}\) 表示从 \((i,j)\) 往下走到第 \(n\) 行最高得分。
• 转移：\(dp_{i,j}=\max(dp_{i+1,j},dp_{i+1,j+1})+a_{i,j}\)。
• 拓扑序：由于 \(i\) 由 \(i+1\) 转移而来，拓扑序就是 \(i\) 从大到小。
• 初始状态：对于 \(1\leqslant i\leqslant n\)，\(dp_{n,i}=a_{n,i}\)。
• 目标状态：\(dp_{1,1}\)。

时间复杂度：\(O(n^2)\)，空间复杂度：\(O(n^2)\)。

序列 dp：最长上升子序列 LIS

P1020 导弹拦截 tips:这题求的两个分别是最长不上升子序列和最长上升子序列，详细证明自己搜。

B3637 最长上升子序列 tips:模板题，数据范围很小，\(O(n^2)\) 可过。

给定一个长度为 \(n\) 的序列 \(a\)，求它最长上升子序列长度。

数据范围：\(1\leqslant n \leqslant 5000, 1\leqslant a_i \leqslant 10^9(1\leqslant i \leqslant n)\)。

令 \(a_0=0\)。

• 状态：\(dp_i\) 表示以第 \(i\) 个元素结尾的最长上升子序列长度。
• 转移：\(dp_i=\max\limits_{0\leqslant j < i \&\& a_j < a_i}\{dp_j\}+1\)。
• 拓扑序：由于 \(dp_i\) 只由 \(0\sim i-1\) 转移而来，拓扑序就是 \(i\) 从小到大。
• 初始状态：\(dp_0=0\)。
• 目标状态：\(\max\limits_{1\leqslant i \leqslant n}\{dp_i\}\)。

时间复杂度：\(O(n^2)\)，空间复杂度：\(O(n)\)。

在这个数据范围中，\(O(n^2)\) 可过，但如果 \(1\leqslant n \leqslant 10^5\) 怎么办呢？

这也好办，只要写个离散化+树状数组/线段树优化就行了。

tips:其实这个可以贪心+二分，但不属于 dp，不谈。

时间复杂度：\(O(n\log n)\)，空间复杂度：\(O(n)\)。

序列 dp：最长公共子序列 LCS

P1439 【模板】最长公共子序列 tips:本题表面上求的是 LCS，实际为 LIS，但 50pts 暴力可以 \(O(n^2)\) LCS 求。

给出一个长度为 \(n\) 的序列 \(a\)，还有一个长度为 \(m\) 的序列 \(b\)，求 \(a\) 和 \(b\) 的最长公共子序列长度。

数据范围：\(1\leqslant n,m \leqslant 5000,1\leqslant a_i,b_j \leqslant 10^9(1\leqslant i \leqslant n,1\leqslant j \leqslant m)\)。

• 状态：\(dp_{i,j}\) 表示 \(a\) 的前 \(i\) 个元素和 \(b\) 的前 \(j\) 个元素的最长公共子序列长度。
• 转移：\(dp_{i,j}=\begin{cases}\max(dp_{i-1,j},dp_{i,j-1}) & a_i \ne b_j\\ dp_{i-1,j-1}+1 & a_i=b_j \end{cases}\)。
• 拓扑序：\(i\) 从小到大，\(i\) 相同则 \(j\) 从小到大。
• 初始状态：对于 \(1\leqslant i \leqslant n,dp_{i,0}=0\)，对于 \(1\leqslant i \leqslant m,dp_{0,i}=0\)，\(dp_{0,0}=0\)。
• 目标状态：\(dp_{n,m}\)。

时间复杂度：\(O(n \times m)\)，空间复杂度：\(O(n \times m)\)。

关于 P1439：由于给定的是两个 \(1\sim n\) 的序列，所以对于两个数 \(a_i,a_j(i<j)\)，如果它们可以在两序列的公共子序列中，那么必然在 \(b\) 序列中的 \(a_i\) 的位置小于 \(a_j\) 的位置，令 \(c_i\) 为 \(b\) 序列中 \(a_i\) 的位置，答案就是 \(c\) 的最长上升子序列长度，用树状数组优化即可。

时间复杂度：\(O(n \log n)\)，空间复杂度：\(O(n)\)。

背包 dp：01 背包

P1048 采药 模板题。

01 背包的模型就是给出 \(n\) 个物品的占用空间 \(a_i\) 和价值 \(b_i\)，对于每个物品，都可以选或者不选，问在给定的背包容量 \(m\) 下最大获得的价值和。

• 状态：\(dp_{i,j}\) 表示考虑完前 \(i\) 个物品(草药)，耗费的背包容量(时间)为 \(j\) 所获得的最大价值和。
• 转移：\(dp_{i,j}=\begin{cases} dp_{i-1,j}& 1\leqslant j < a_i\\ \max(dp_{i-1,j},dp_{i-1,j-a_i}+b_i) & a_i \leqslant j \leqslant m\end{cases}\)
• 拓扑序：\(i\) 从小到大。
• 初始状态：\(dp_{0,0} = 0\)。
• 目标状态：\(dp_{n,m}\)。

时间复杂度：\(O(n \times m)\)，空间复杂度：\(O(n \times m)\)。

背包 dp：多重背包

U280382 多重背包问题 别人造的例题。

多重背包的模型就是给出 \(n\) 个物品的占用空间 \(a_i\)、价值 \(b_i\) 和选择的个数 \(c_i\)，对于每个物品，都可以选 \(0\sim c_i\)，问在给定的背包容量 \(m\) 下最大获得的价值和。

• 状态：\(dp_{i,j}\) 表示考虑完前 \(i\) 个物品，耗费的背包容量为 \(j\) 所获得的最大价值和。
• 转移：分为两种解法，见下方。
• 拓扑序：\(i\) 从小到大。
• 初始状态：\(dp_{0,0}=0\)。
• 目标状态：\(dp_{n,m}\)。

solution 1

转移方法：暴力。

\(dp_{i,j}=\max\limits_{0\leqslant k \leqslant c_i \&\& j \geqslant k \times a_i}\{ dp_{i-1,j-k\times a_i}+k\times b_i\}\)。

时间复杂度：\(O(m \times \sum\limits_{1\leqslant i \leqslant n} c_i)\)，空间复杂度：\(O(n\times m)\)。

如果 \(\sum\limits_{1\leqslant i \leqslant n} c_i\) 比较大则完全接受不了，那么就需要考虑 solution 2。

solution 2

转移方法：拆分 \(c_i\) 转 01 背包。

众所周知，如果你有了 \(1,2,4,8 \cdots 2^k\)，那么你可以用每个元素不超过 \(1\) 次凑出来 \(0\sim 2^{k+1}-1\) 中所有整数，那么考虑把 \(c_i\) 尽量拆成 \(1,2,4\cdots\)，先拆一遍，最后剩下一部分单独考虑，这下就可以凑出来 \(0\sim c_i\) 中的所有整数了。

01 背包转移见上方。

时间复杂度：\(O(m\times (n + \sum\limits_{1\leqslant i \leqslant n}\log c_i))\)，空间复杂度：\(O(n\times m)\)。

背包 dp：完全背包

P1616 疯狂的采药 模板题。

个人感觉比多重背包简单。

完全背包的模型就是给出 \(n\) 个物品的占用空间 \(a_i\)、价值 \(b_i\)，对于每个物品，都可以选无限多个，问在给定的背包容量 \(m\) 下最大获得的价值和。

• 状态：\(dp_{i,j}\) 表示考虑完前 \(i\) 个物品，耗费的背包容量为 \(j\) 所获得的最大价值和。
• 转移：\(dp_{i,j}=\begin{cases} dp_{i-1,j}& 1\leqslant j \leqslant a_i\\ dp_{i,j}=\max(dp_{i-1,j},dp_{i,j-a_i}+b_i) & a_i \leqslant j \leqslant m\end{cases}\)。
• 拓扑序：\(i\) 从小到大，\(i\) 相同时 \(j\) 从小到大。
• 初始状态：\(dp_{0,0}=0\)。
• 目标状态：\(dp_{n,m}\)。

解释一下转移，由于每个物品可以无限选择，那么直接调用 \(dp_{i,j-a_i}\) 相当于再选一个，而之前并没限定选择几个，这就完美地处理了无限个物品。

时间复杂度：\(O(n \times m)\)，空间复杂度：\(O(n \times m)\)。

背包 dp：分组背包

P1757 通天之分组背包 模板题。

其实和 01 背包差不多，只要把它门分个组存储，每个组选一个处理 01 背包即可。

区间 dp

P1775 石子合并（弱化版） 敲门砖，模板题。

P1880 石子合并 标准版，模板题。

区间 dp，维护的信息为一段区间的最优化属性。

在石子合并弱化版中，为了让代价尽量小，每一段区间的代价都要尽可能小。

• 状态：\(dp_{l,r}\) 表示将 \([l,r]\) 合并成一堆石子的最小代价。
• 转移：\(dp_{l,r}=\min\limits_{l\leqslant i < r}\{dp_{l,i}+dp_{i+1,r}\}+\sum\limits_{l\leqslant i \leqslant r}m_i\)。
• 拓扑序：\(r-l\) 从小到大。
• 初始状态：对于每个 \(1\leqslant i \leqslant n\)，\(dp_{i,i}=0\)。
• 目标状态：\(dp_{1,n}\)。

时间复杂度：\(O(n^3)\)，空间复杂度：\(O(n^2)\)。

石子合并的标准版中，则是将一排变成了一个环，本质没区别，只要一个环形题的常见优化套路：断环成链即可。

时间复杂度：\(O(8\times n^3)\)，空间复杂度：\(O(4\times n^2)\)。

dp 优化

滚动数组

通过数组的滚动来实现空间优化的目的，在 \(dp_{i,\cdots}\) 只和 \(dp_{i-1,\cdots}\) 有关时，通常可以滚动成两个数组，方便处理。

当然还有一个叫做自我滚动的东西，只要注意好拓扑序是否满足只与 \(i\) 有关，以及自我滚动后的拓扑序即可。

记忆化搜索

并不是传统意义上的优化，但它能让你的代码逻辑更加清晰。

就是在搜索时记录当前情况下的最优解，当下一次访问时直接返回结果即可。

缺点就是递归常数大一些。

树形 dp

P1352 没有上司的舞会 经典的节点选择型。

树形 dp，就是把 dp 建立于树的形态之上，通常 \(dp_i\) 都是 \(i\) 及 \(i\) 的子树范围内的最优化属性。

大致可以分类为节点选择型和树上背包型，还有换根 dp 比较恶心。

在 P1352 中，每个节点都可以选或不选，但选出来的点之间不能有边相连。

• 状态：\(dp_{i,0}\) 表示节点 \(i\) 不选的最大欢乐指数，\(dp_{i,1}\) 表示节点 \(i\) 选的最大欢乐指数。
• 转移：令 \(son_i\) 表示节点 \(i\) 的儿子集合，则 \(dp_{i,0}=\sum\limits_{1\leqslant j\leqslant n\&\& j\in son_i} \max(dp_{j,0}, dp_{j,1}),dp_{i,1}=\sum\limits_{1\leqslant j\leqslant n\&\& j\in son_i} dp_{j,0}+r_i\)。
• 拓扑序：首先找到那个没有上司的节点，以它为根，按深度从大到小进行 \(dp\)，也可以直接边搜索边做。
• 初始状态：没有。
• 目标状态：\(\max(dp_{根,0},dp_{根,1})\)。

时间复杂度：\(O(n)\)，空间复杂度：\(O(n)\)。

状压 dp

CSES1690 Hamiltonian Flights 模板。

状压 dp，就是把多维状态压缩成一个整数，通常是把每个节点的访问情况通过二进制的形式压缩成整数。

其实还算简单的，配合之前的 dp，将多维度压缩整数，注意细节即可。

强连通分量和 Tarjan

强连通分量(Strongly Connected Components，SCC)，指的是极大的连通子图。

tarjan 算法，用于求图的强连通分量。

dfs 生成树

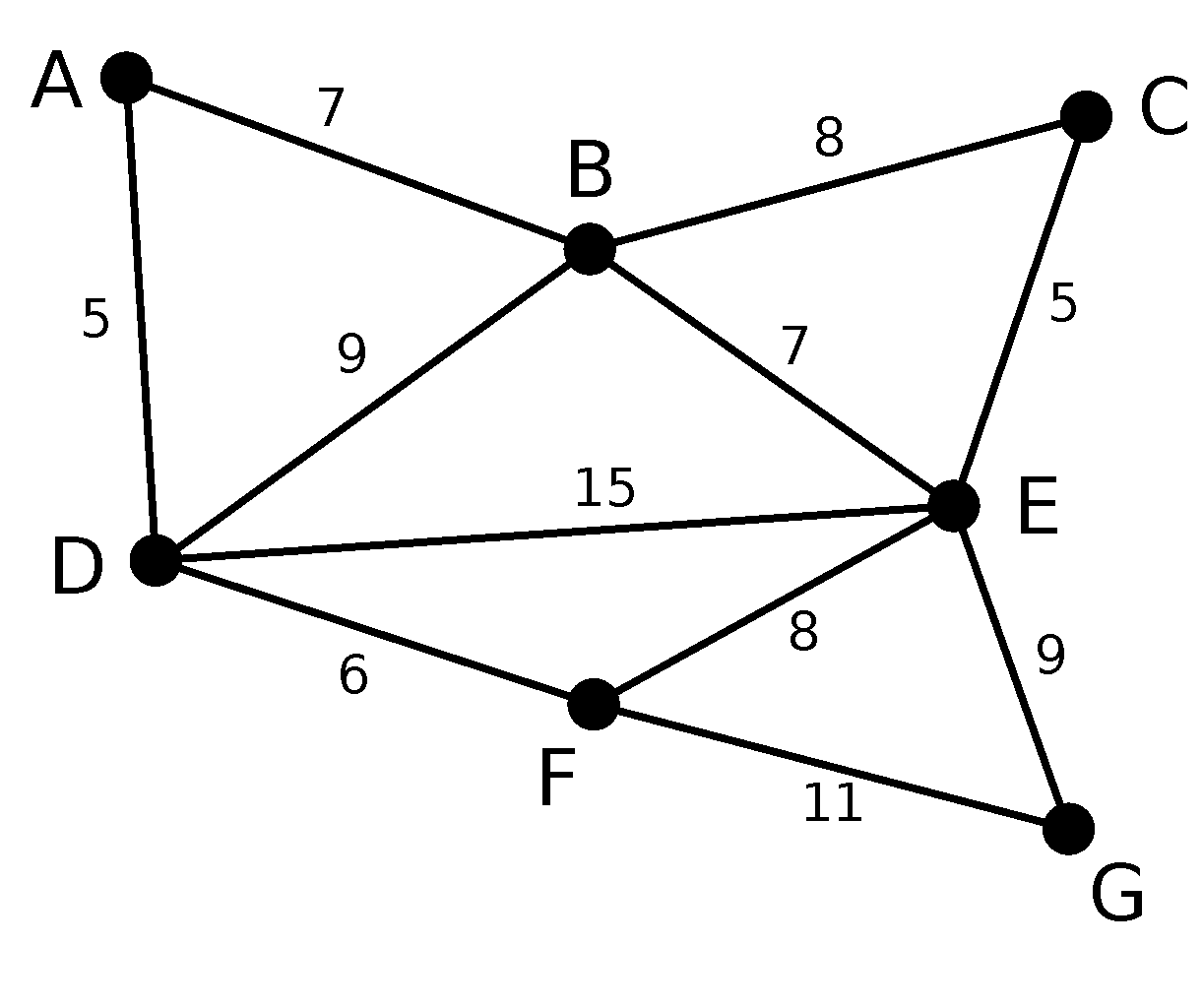
有向图的 dfs 生成树大致分为四种边：

• 树边(tree edge)：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
• 反祖边(back edge)：示意图中以红色边表示(即 \(7 \rightarrow 1\))，也被叫做回边，即指向祖先结点的边。
• 横叉边(cross edge)：示意图中以蓝色边表示(即 \(9 \rightarrow 7\))，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
• 前向边(forward edge)：示意图中以绿色边表示（即 \(3 \rightarrow 6\))，它是在搜索的时候遇到子树中的结点的时候形成的。

如果结点 \(u\) 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 \(u\) 为根的子树中。结点 \(u\) 被称为这个强连通分量的根。

反证法：假设有个结点 \(v\) 在该强连通分量中但是不在以 \(u\) 为根的子树中，那么 \(u\) 到 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 \(u\) 是第一个访问的结点矛盾了。得证。

Tarjan 求强连通分量

需要对每个节点 \(u\) 都维护以下几个信息：

• \(dfn_u\)：\(u\) 在深度优先搜索时是第几个被访问的(人称豆腐脑序)。
• \(low_u\)：在 \(u\) 的子树中能够回溯到的最早的在栈中的结点。

很明显，对于每个 \(u\) 的后代 \(i\) 都有 \(dfn_u < dfn_i\)。从根开始的一条路径上的 \(dfn\) 严格递增，\(low\) 严格非降。

用 dfs 来求 \(dfn\) 和 \(low\)，每搜索到一个新的节点就让它入栈，每找到一个强连通分类，就让它们出栈。

当节点 \(u\) 向节点 \(v\) 做遍历时，有三种情况：

• \(v\) 未被访问，则对 \(v\) 进行 dfs，回溯时 low[u] = min(low[u], low[v]); 因为存在从 \(u\) 到 \(v\) 的直接路径，所以 \(v\) 能够回溯到的已经在栈中的结点，\(u\) 也一定能够回溯到。
• \(v\) 已被访问且仍在栈中，那么 low[u] = min(low[u], dfn[v]);
• \(v\) 被访问过且已不在栈中，说明 \(v\) 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

处理完以后，我们可以想到在一个强连通分量里有且仅有一个点 \(u\) 满足 \(dfn_u=low_u\)，该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 \(dfn\) 和 \(low\) 值最小，不会被该连通分量中的其他结点所影响。

所以只要在回溯的过程中判断 \(dfn_u\) 是否和 \(low_u\) 相等，若相等，则栈内 \(u\) 及它上方的节点构成一个 SCC。

const int N = 1e4 + 10;

int n, dfncnt, dfn[N], low[N], bel[N], stk[N], top, fstk[N], sc, sz[N], b[N], ans, sum, c[N];
vector<int> g[N];

void tarjan (int x) {
  dfn[x] = low[x] = ++dfncnt, fstk[x] = 1, stk[++top] = x;
  for (int i : g[x]) {
    if (!dfn[i]) {
      tarjan(i), low[x] = min(low[x], low[i]);
    } else if (fstk[i]) {
      low[x] = min(low[x], dfn[i]);
    }
  }
  if (dfn[x] == low[x]) {
    ++sc;
    while (1) {
      sz[sc]++, fstk[stk[top]] = 0, bel[stk[top--]] = sc;
      if (stk[top + 1] == x) {
        break;
      }
    }
  }
}

应用

我们可以将每个强连通分量都压缩成一个点(缩点)，那么原图就会变成 DAG，可以进行拓扑排序等。

例题

P2746 [USACO5.3] 校园网Network of Schools | #10091. 「一本通 3.5 例 1」受欢迎的牛

割点和割边

割点

对于一个无向图，如果把这个点删除后这个图的极大连通分量数增加了，那么这个点就是原图的割点(割顶)。

举个例子，这张图内的割点明显只有 \(2\)。

首先我们先通过 DFS 给它们打上时间戳：

记录在 \(dfn\) 中，还需要另外一个数组 low，用它来存储不经过其父亲能到达的最小的时间戳。

好，和 Tarjan 扯上关系了，那么首先 Tarjan 预处理一下，可以得到定理：对于某个顶点 \(u\)，如果存在至少一个顶点 \(v\)(\(u\) 的儿子)，使得 \(low_v \geqslant dfn_u\)，即不能回到祖先，那么 \(u\) 点为割点。

但是对于搜索树的根节点需要特殊处理：若该点不是割点，则其他路径亦能到达全部结点，因此从起始点只「向下搜了一次」，即在搜索树内仅有一个子结点。如果在搜索树内有两个及以上的儿子，那么他一定是割点了(设想上图从 \(2\) 开始搜索，搜索树内应有两个子结点：\(3\) 或 \(4\) 及 \(5\) 或 \(6\))。如果只有一个儿子，那么把它删掉，不会有任何的影响。比如下面这个图，此处形成了一个环。

#include <bits/stdc++.h>

using namespace std;

const int N = 2e4 + 10;

int n, m, dfncnt, dfn[N], low[N], bel[N], stk[N], top, fstk[N], sc, sz[N], cnt;
vector<int> g[N];
bool ans[N];

void tarjan (int x, int fa) {
  int son = 0;
  dfn[x] = low[x] = ++dfncnt, fstk[x] = 1, stk[++top] = x;
  for (int i : g[x]) {
    if (!dfn[i]) {
      son++;
      tarjan(i, x), low[x] = min(low[x], low[i]);
      if (fa != x && low[i] >= dfn[x] && !ans[x]) {
        ans[x] = 1, cnt++;
      }
    } else if (i != fa) {
      low[x] = min(low[x], dfn[i]);
    }
  }
  if (fa == x && son >= 2 && !ans[x]) {
    ans[x] = 1, cnt++;
  }
}

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for (int i = 1, x, y; i <= m; i++) {
    cin >> x >> y, g[x].push_back(y), g[y].push_back(x);
  }
  for (int i = 1; i <= n; i++) {
    if (!dfn[i]) {
      dfncnt = 0, tarjan(i, i);
    }
  }
  cout << cnt << '\n';
  for (int i = 1; i <= n; i++) {
    if (ans[i]) {
      cout << i << ' ';
    }
  }
  return 0;
}

模板题 Link

割边

对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。严谨来说，就是：假设有连通图 \(G=\{V,E\}\)，\(e\) 是其中一条边(即 \(e \in E\))，如果 \(G-e\) 是不连通的，则边 \(e\) 是图 \(G\) 的一条割边(桥)。

比如下图中红色边就是割边。

和割点差不多，不需要特殊考虑更根节点，只要把 \(low_v \geqslant dfn_u\) 改为 \(low_v > dfn_u\) 即可。

void tarjan (int x, int fa) {
  int son = 0;
  dfn[x] = low[x] = ++dfncnt, fstk[x] = 1, stk[++top] = x;
  for (int i : g[x]) {
    if (!dfn[i]) {
      son++;
      tarjan(i, x), low[x] = min(low[x], low[i]);
      if (low[i] > dfn[x] && !ans[x]) {
        ans[x] = 1, cnt++;
      }
    } else if (i != fa) {
      low[x] = min(low[x], dfn[i]);
    }
  }
}

拓扑排序

OI-wiki Link

众所周知，拓扑序可以决定 dp 的顺序，而拓扑排序则是用于求图上的点的拓扑序。

对于图上任意两点 \(x,y(x\ne y)\)，当 \(x\) 的拓扑序大于 \(y\) 的拓扑序时，\(x\) 不能到达 \(y\)。所以在有向有环图和无向图上是不存在拓扑序的。

而拓扑排序则是用于求 DAG(有向无环图)的拓扑序。

思想

从小到大分配拓扑序。

对于一个节点 \(x\)，如果它的入度为 \(0\)，那么就代表在原图上所有可以到达 \(x\) 的点的拓扑序都小于 \(x\) 的拓扑序，那么就删除节点 \(x\)，继续进行下一次分配。

实现

用一个队列来维护入度为 \(0\) 的节点。

首先把所有原图中的入度为 \(0\) 压入队列，然后每次取出队头元素 \(x\)，删除它。

删除就是将所有 \(x\) 连向的节点的入度减 \(1\)，如果其中有一个节点的入度变为 \(0\) 了，将其压入队列即可。

B3644 【模板】拓扑排序 / 家谱树

虽然这题 \(n\) 范围很小，但是就把它当 \(10^5\) 这种级别来做。

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int n, x, b[110];
vector<int> g[110];
queue<int> q;

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++) {
    while (cin >> x && x) {
      g[i].push_back(x), b[x]++;
    }
  }
  for (int i = 1; i <= n; i++) {
    if (!b[i]) {
      q.push(i);
    }
  }
  for (int i = 1; i <= n; i++) {
    x = q.front();
    q.pop();
    cout << x << ' ';
    for (int j : g[x]) {
      b[j]--;
      if (!b[j]) {
        q.push(j);
      }
    }
  }
  return 0;
}

令 \(n\) 为节点数，\(m\) 为边数，所有复杂度为 \(O(n+m)\)。

一些应用

• 拓扑序决定了 dp 的顺序，因此当要做图上 dp 时可以直接边拓扑排序边 dp。
• 给定一个有向图，可以通过拓扑排序来判环，当拓扑排序后仍有节点没有被规定拓扑序时就是有环。

欧拉路

OI-wiki Link

定义

欧拉回路：经过每条边恰好一次后回到起点的路径。

欧拉通路：经过每条边恰好一次后没有回到起点的路径。

欧拉图：具有欧拉回路的图。

半欧拉图：不具有欧拉回路但具有欧拉通路的图。

判别

如果图不连通，必然不是欧拉/半欧拉图。

• 无向图为欧拉图，当且仅当：所有点的度数都是偶数。

• 无向图为半欧拉图，当且仅当：有两个点度数为奇数(这两个点分别就是起点和终点)，其余为偶数。

• 令有向图一个点的度数为它的出度减入度。

  • 有向图为欧拉图，当且仅当：所有点的度数都为 \(0\)。
  • 有向图为半欧拉图，当且仅当：有两个点度数分别为 \(1\) 和 \(-1\)(这两个点分别就是起点和终点)，其余为 \(0\)。

找欧拉回/通路

见 OI-wiki，我一直没看懂怎么搞的。

最短路

OI-wiki Link

最短路问题，顾名思义就是要求图上的某点到另外一点的最短距离，爆搜就不用说了。

令图上点数为 \(n\)，边数为 \(m\)。

由于考虑的是最短路，那么包含负环的图就不能算了，没有最短这一说。

正权图最短路性质：任意两点间的最短路都不会经过重复的点和重复的边。

$$\texttt{Floyd}$$

优点

Floyd 可以求出两两节点间的最短路，码量较低，可以找到负权图的最短路。

缺点

时间复杂度高。

令 f[k][i][j] 表示在只经过(\(i\) 和 \(j\) 不算) \(1\sim k\) 的点的情况下 \(i\) 到 \(j\) 的最短路，显然 f[n][i][j] 就是原图上 \(i,j\) 之间最短路长度。

初始时 \(f_{0,i,j}=\begin{cases}0&i=j\\边权&i和j直接相连\\+\infty&i和j不相连 \end{cases}\)，接着三重循环枚举 \(k,i,j(1\leqslant k,i,j \leqslant n)\)，f[k][i][j] = min(f[k - 1][i][j], f[k - 1][i][k] + f[k - 1][k][j])。

优化一下，第一维对结果无影响，变为二维 f[i][j]。

时间复杂度：\(O(n^3+m)\)，空间复杂度：\(O(n^2)\)

$$\texttt{Bellman-Ford}$$

优点

可以找到负权图的单源最短路，可以判负环。

缺点

时间复杂度仍比较高。

松弛操作：对于边 \(u\xrightarrow{w} v\)，\(dis_v=\min(dis_v, dis_u+ w)\)，如果\(dis_v\) 发生了改变，就称为松弛成功。

Bellman-Ford 就是不断尝试松弛图上的边，每次循环都枚举每条边，看是否能松弛，如果所有的边都无法松弛了，那么最短路也就求完了。

在最短路存在的情况下，最多只会经过 \(n -1\) 条边，那么松弛的次数也就不会超过 \(n-1\)，当第 \(n\) 次松弛还能有松弛成功的点，就代表从原点开始能到达一个负环。

tips:如果想用 Bellman-Ford 判负环，那么最保守的方法是建立一个超级原点，向每个节点都连一条边权为 \(0\) 的边，在以它为原点做 Bellman-Ford 即可。

时间复杂度：\(O(n\times m)\)，空间复杂度：\(O(n+m)\)。

队列优化 SPFA

关于 SPFA，它死了。

很显然，只有上一轮被更新的节点所连出去的边，才有可能是可以松弛的边，可以用队列维护哪些节点可能引起松弛操作。

SPFA 大多数情况下跑到快，可最差仍然是 \(O(n\times m)\) 的。

$$\texttt{Dijkstra}$$

优点

时间复杂度低，可以求出单源或者多源最短路。

缺点

一遇到负权就寄。

主要思想：使用优先队列存储一些访问到的节点的编号和最短路长度，优先队列肯定按最短路长度从小到大。

当取出了一个队头时，如果这个节点没有被取出来过，那么就记录好答案，将它所连出去的边都进行一次松弛。

当松弛 \(u\xrightarrow{w} v\) 时，如果 \(v\) 已经被取出来过，那么就不用放入优先队列了，因为在它之前的节点的最短路长度必然是非严格小于它的，不可能更优。

时间复杂度：\(O(m\log m)\)，空间复杂度：\(O(n+m)\)。

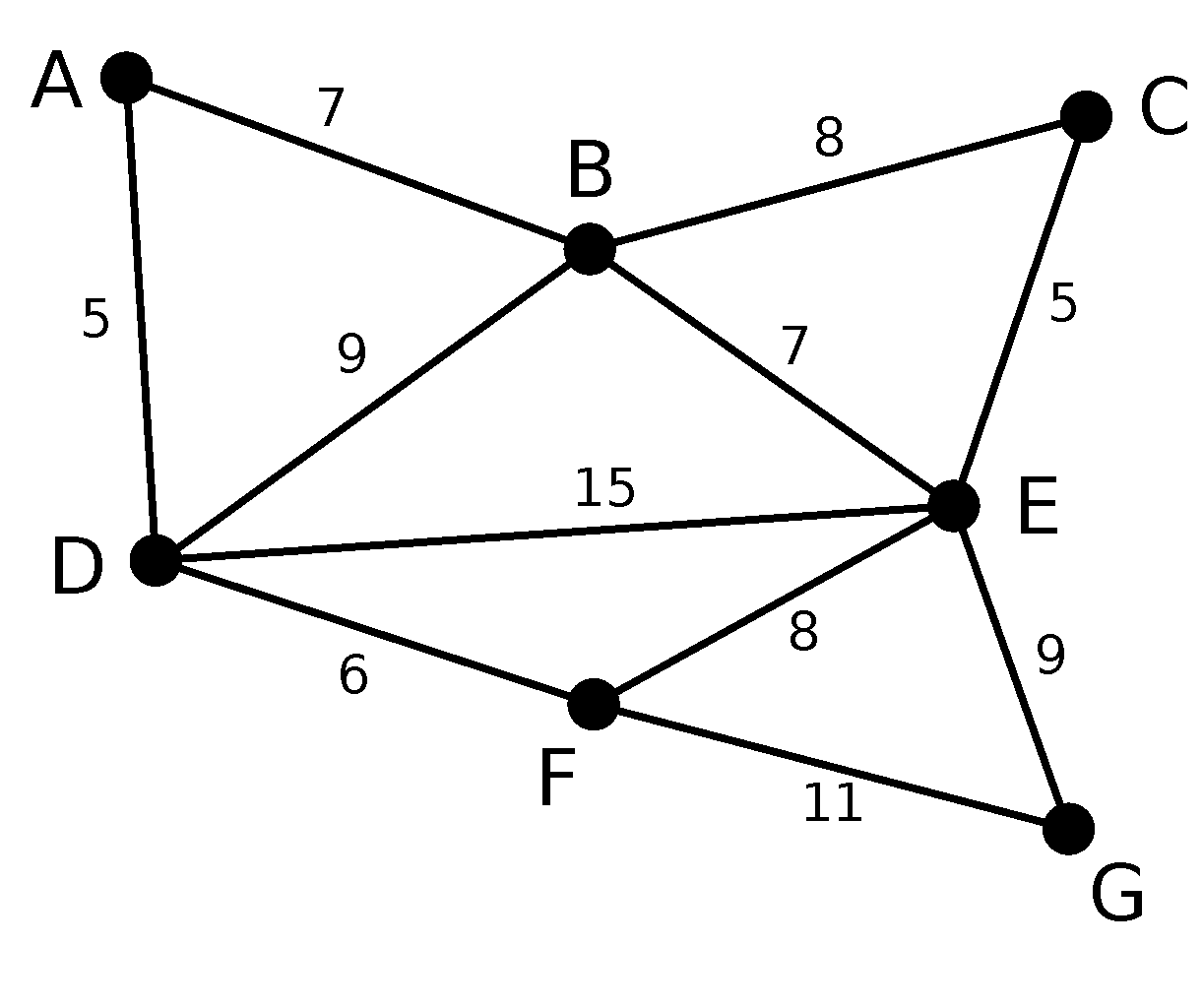
最小生成树

OI-wiki Link

最小生成树，就是图上边权和最小的生成树。

令 \(n\) 为图上节点数，\(m\) 为图的边数。

$$\texttt{Kruskal}$$

克鲁斯卡尔算法，一种常见且方便好写的最小生成树算法，利用贪心的思想+并查集维护。

贪心就是按边权从小到大排序，依次处理。如果当前边的两个端点处于同一棵树内，那么就不能加这条边(否则会形成环，不满足生成树的要求)，否则将这条边连起来。

判断两点是否处于同一棵树内，这不就是并查集所维护的吗？

排序：\(O(m\log m)\)，并查集就看写的是什么了。空间复杂度：\(O(n+m)\)。

$$\texttt{Prim}$$

Prim 是另外一种常见且码量也不算很多的最小生成树算法，主要思想就是维护每个点到生成树内的点的最短距离，每次把距离最小的加入最小生成树。

加入距离最小的点，这个也可以用优先队列维护，但它复杂度并没有更优，常数也比 Kruskal 要大，所以一般非必要情况下不会写 Prim。

次小生成树

非严格次小生成树

令图的最小生成树为 \(T\)，那么对于每条非树边 \((u,v,w)\)，找到 \(T\) 中 \(u\) 到 \(v\) 路径上的边权最大的一条边，把它删掉，再加入 \((u,v,w)\)，就可以得到一棵新的生成树，取这些新的生成树中边权之和最小的即可。

维护 \(u,v\) 路径上的边权最大值也很简单，首先预处理，然后每次倍增 LCA 即可。

严格次小生成树

观察原本的算法，为啥它是非严格的呢？因为可能这条路径上的最大值恰好等于 \(w\)，此时边权之和没有改变，所以是非严格的。

解决方法也很简单，只要在维护最大值时顺便维护一个严格次大值，当最大值等于 \(w\) 时则用严格次大值来替换。

细节不少，D 了我至少一个小时。

struct MST {
  vector<pair<int, int>> g[N];
  int fa[N][25], mx[N][25][2], h[N];
  void Add (int x, int y, int z) {
    g[x].push_back({y, z}), g[y].push_back({x, z});
  }
  void MkTe (int x) {
    h[x]++;
    for (auto i : g[x]) {
      if (i.first != fa[x][0]) {
        fa[i.first][0] = x, mx[i.first][0][0] = i.second, mx[i.first][0][1] = -1, h[i.first] = h[x], MkTe(i.first);
      }
    }
  }
  void FAT () {
    for (int i = 0; i <= 20; i++) {
      mx[0][i][0] = mx[0][i][1] = -1;
    }
    for (int i = 1; i <= 20; i++) {
      for (int j = 1; j <= n; j++) {
        fa[j][i] = fa[fa[j][i - 1]][i - 1], mx[j][i][0] = mx[j][i - 1][0], mx[j][i][1] = mx[j][i - 1][1];
        if (mx[fa[j][i - 1]][i - 1][0] > mx[j][i][0]) {
          mx[j][i][1] = mx[j][i][0], mx[j][i][0] = mx[fa[j][i - 1]][i - 1][0];
        } else if (mx[fa[j][i - 1]][i - 1][0] < mx[j][i][0] && mx[fa[j][i - 1]][i - 1][0] > mx[j][i][1]) {
          mx[j][i][1] = mx[fa[j][i - 1]][i - 1][0];
        }
        if (mx[fa[j][i - 1]][i - 1][1] < mx[j][i][0] && mx[fa[j][i - 1]][i - 1][1] > mx[j][i][1]) {
          mx[j][i][1] = mx[fa[j][i - 1]][i - 1][1];
        }
      }
    }
  }
  pair<int, int> lca (int x, int y) {
    if (h[x] > h[y]) {
      swap(x, y);
    }
    pair<int, int> xm = {-1, -1};
    for (int i = 20; i >= 0; i--) {
      if ((h[y] - h[x]) >> i) {
        if (mx[y][i][0] > xm.first) {
          xm.second = xm.first, xm.first = mx[y][i][0];
        } else if (mx[y][i][0] < xm.first && mx[y][i][0] > xm.second) {
          xm.second = mx[y][i][0];
        }
        if (mx[y][i][1] < xm.first && mx[y][i][1] > xm.second) {
          xm.second = mx[y][i][1];
        }
        y = fa[y][i];
      }
    }
    if (x == y) {
      return xm;
    }
    for (int i = 20; i >= 0; i--) {
      if (fa[x][i] != fa[y][i]) {
        if (mx[y][i][0] > xm.first) {
          xm.second = xm.first, xm.first = mx[y][i][0];
        } else if (mx[y][i][0] < xm.first && mx[y][i][0] > xm.second) {
          xm.second = mx[y][i][0];
        }
        if (mx[y][i][1] < xm.first && mx[y][i][1] > xm.second) {
          xm.second = mx[y][i][1];
        }
        if (mx[x][i][0] > xm.first) {
          xm.second = xm.first, xm.first = mx[x][i][0];
        } else if (mx[x][i][0] < xm.first && mx[x][i][0] > xm.second) {
          xm.second = mx[x][i][0];
        }
        if (mx[x][i][1] < xm.first && mx[x][i][1] > xm.second) {
          xm.second = mx[x][i][1];
        }
        y = fa[y][i], x = fa[x][i];
      }
    }
    if (mx[y][0][0] > xm.first) {
      xm.second = xm.first, xm.first = mx[y][0][0];
    } else if (mx[y][0][0] < xm.first && mx[y][0][0] > xm.second) {
      xm.second = mx[y][0][0];
    }
    if (mx[y][0][1] < xm.first && mx[y][0][1] > xm.second) {
      xm.second = mx[y][0][1];
    }
    if (mx[x][0][0] > xm.first) {
      xm.second = xm.first, xm.first = mx[x][0][0];
    } else if (mx[x][0][0] < xm.first && mx[x][0][0] > xm.second) {
      xm.second = mx[x][0][0];
    }
    if (mx[x][0][1] < xm.first && mx[x][0][1] > xm.second) {
      xm.second = mx[x][0][1];
    }
    return xm;
  }
} mst;

数论

白皮书第 6 章，进阶指南 0x03。

0xFF 一些链接

\(\color{red}\texttt{【数学2-1】进阶数论}\) | \(\color{red}\texttt{《算法竞赛进阶指南》第四章—数学知识}\) | \(\color{red}\texttt{OI-wiki-数学}\)

0x00 取模

模运算，常用于大数计算，当答案数值非常大时，通常会有两种情况，第一种是取模，通过模上一个较小的数来方便输出和计算；还有一种是高精度，有这个的题目就会比较恶心。

取模有以下性质：

1. 可加性：\(\texttt{(a + b) mod m = ((a mod m) + (b mod m)) mod m}\)
2. 可减性：\(\texttt{(a - b) mod m = ((a mod m) - (b mod m)) mod m}\)，c++实现时为了避免出现负数，通常要在括号中加上模数 \(m\)
3. 可乘性：\(\texttt{(a}\, \times\, \texttt{b) mod m = ((a mod m)}\, \times \, \texttt{(b mod m)) mod m}\)
4. 没有可除性！除法取模等于乘除数的逆元。

0x01 乘法取模

两数直接乘，可能导致爆 long long 导致寄掉(噢当然你可以用 __int128，数据实在太大则考虑是否需要使用高精度)，这里给出一个不一定在所有情况下都有用的解决办法。

原理：\(x \times y\) 会爆，可以考虑变成 \((x \times 2) \times (y\ /\ 2)\)，然后变成 \((x \times 2^2) \times (y\ /\ 2^2)\)，以此类推，直到 \(y = 0\)，详细证明见白皮书第 \(389\) 页。

如果 \(x\) 还是不幸爆炸了，那么就需要考虑高精度，但这个做法基本上可以规避掉大部分情况。

using ll = long long;

ll mul (ll x, ll y, ll mod) { // (x * y) % mod
  x %= mod, y %= mod; // 首先规避一下
  ll res = 0;
  while (y) {
    if (y & 1) { // 判断奇偶性
      res = (res + x) % mod;
    }
    x = x * 2 % mod, y >>= 1;
  }
  return res;
}

0x10 快速幂

OI-wiki-快速幂

计算 \(x^n \bmod m\)，朴素算法当然是一个个数去乘，边乘边取模，时间复杂度 \(O(n)\)，十分不优秀。

一种做法是分治法，看白皮书去。

另一种就是位运算，时间复杂度 \(O(\log n)\)，十分优秀，是标准的做法。

举个例子，求 \(a^{11}\ =\ ?\)，朴素算法当然能做，但肯定不会去讲。

将 \(a^{11}\) 分解成 \(a^8 \times a^2 \times a\)，每个数的幂次都是 \(2\) 的倍数。 那么就可以方便地计算了。

求幂次，用二进制分解，\(11 = (1011)_2\)，跳过 \(a^4\) 即可。

具体实现看代码。

using ll = long long;

ll qmod (ll x, ll y, ll mod) { // x ^ y % mod
  ll sum = 1;
  while (y) {
    if (y % 2) {
      sum = (sum * x) % mod;
    }
    y >>= 2, x = (x * x) % mod;
  }
  return sum;
}

0x20 gcd 和 lcm

OI-wiki-最大公约数

最大公约数和最小公倍数研究整除等问题，也可以用在概率问题的分数通分等等。

备注：

• 最大公约数，\(\texttt{Greatest Common Divisor(GCD)}\)，\(\texttt{Greatest Common Denominator(GCD)}\)，\(\texttt{Greatest Common Factor(GCF)}\)，\(\texttt{Highest Common Factor(HCF)}\)
• 最小公倍数，\(\texttt{Least Common Multiple(LCM)}\)

0x21 GCD

整数 \(a\) 与 \(b\) 的最大公约数，就是一个最大的整数 \(c\) 且 \(c \mid a\)、\(c \mid b\)，记作 \(\gcd(a,b)\)。

注意，因为是最大公约数，而 \(\left\vert a\right\vert\) 又是 \(a\) 的约数(\(a\) 无论是负数或非负数)，所以对于任意的 \((a,b)\)，有 \(\gcd(a,b) = \gcd(\left\vert a\right\vert, \left\vert b\right\vert)\)。

GCD有以下性质：

1. \(\gcd(a,b) = gcd(a, k \times a + b)\)
2. \(\gcd(k \times a, k \times b) = k \times \gcd(a,b)\)
3. 多个整数的 GCD：\(\gcd(a,b,c,d) = \gcd(\gcd(a, b), \gcd(c, d))\)，即 GCD 具有交换律和结合律(可以这么叫吧，理解万岁)
4. 若 \(\gcd(a,b) = d\)，则 \(\gcd(\frac{a}{d}, \frac{b}{d}) = 1\)，即 \(\frac{a}{d}\) 与 \(\frac{b}{d}\) 互质
5. \(\gcd(a + c \times b, b) = \gcd(a,b)\)

代码有几种，当然你也可以使用自带的函数 __gcd(a, b)，但要确保 \(a \geqslant 0\) 且 \(b \geqslant 0\)。

\(1^{\texttt{st}}\)欧几里得算法

辗转相除法，是最常用的写法，唯一的缺点就是取模常数太大了，复杂度参考白皮书。

int gcd (int x, int y) {
  return (y ? gcd(y, x % y) : x);
}

极简版

int gcd (int a, int b) {
  while (a ^= b ^= a ^= b %= a) {
  }
  return b;
}

\(2^{\texttt{nd}}\) 更相减损术

基于性质：\(\gcd(a,b)=\gcd(b,a-b)=\gcd(a,a-b)\)。

计算步骤：\(\gcd(a,b)=\begin{cases} a & {a = b}\\\gcd(a-b,b) & {a > b}\\\gcd(a,b - a) & {a < b} \end{cases}\)

int gcd (int x, int y) {
  while (x != y) {
    if (x > y) {
      x -= y;
    } else {
      y -= x;
    }
  }
  return x;
}

更相减损术虽然避免了取模的常数，但在最极端的情况下时间复杂度可以达到 \(O(\max(a,b))\)，实在不够优秀。在求 \(\gcd(10^9,1)\) 时就会爆炸。

\(3^{\texttt{rd}}\) Stein 算法

基于更相减损术，对于一些情况进行讨论和优化，具体如下：

• \(a\) 和 \(b\) 同为偶数，\(\gcd(a,b) = 2 \times \gcd(\frac{a}{2}, \frac{b}{2})\)
• \(a\) 和 \(b\) 同为奇数，\(\gcd(a,b) = \gcd(\frac{a+b}{2}, \frac{a-b}{2})\)
• \(a\) 奇 \(b\) 偶，根据性质 \(2\) 可得 \(\gcd(a,b)=\gcd(\frac{a}{2}, b)\)
• \(a\) 偶 \(b\) 奇，根据性质 \(2\) 可得 \(\gcd(a,b)=\gcd(a,\frac{b}{2})\)

结束条件仍然是 \(a = b\) 时返回 \(a\)。

using ll = long long;

ll gcd (ll a, ll b) {
  if (a < b) {
    return gcd(b, a);
  } else if (a == b) {
    return a;
  }
  if (a % 2 == b % 2) {
    return (a % 2 == 0 ? 2 * gcd(a / 2, b / 2) : gcd((a + b) / 2, (a - b) / 2));
  }
  return (a % 2 == 0 ? gcd(a / 2, b) : gcd(a, b / 2));
}

0x22 LCM

\(\texttt{有 LCM，必有 GCD!!!1}\ \ \ \ \ \ \texttt{——鲁迅}\)

OI-wiki-最小公倍数

推论自己看白皮书，结论就是 \(\texttt{lcm(a,b) = a}\,\times\,\texttt{b / gcd(a,b)}\)

为了防止爆炸，可以先除再乘。

int lcm (int x, int y) {
  return 1ll * x / gcd(x, y) * y;
}

0x23 裴蜀定理

OI-wiki-裴蜀定理

又名贝祖定理(Bézout's lemma)，是关于 GCD 的一个定理。

• 初步定理：若有一个整数二元组 \(\texttt{(x, y)}\)，则必然存在一个整数二元组 \(\texttt{(a, b)}\) 使得 \(a \times x + b \times y = \gcd(x,y)\)，这个等式被称为 Bézout 等式。
• 推论：整数 \(a\) 与 \(b\) 互质当且仅当存在整数 \(x\) 和 \(y\) 使得 \(a \times x + b \times y = 1\)。

0x30 扩展欧几里得算法

OI-wiki-扩展欧几里得算法

简称扩欧(Extended Euclidean algorithm, EXGCD)，常用于求 \(ax + by = c\) 的一组特解，过程自己看OI-wiki或白皮书，代码：

int exgcd (int a, int b, ll &x, ll &y) {
  if (!b) {
    x = 1, y = 0;
    return a;
  }
  int d = exgcd(b, a % b, x, y);
  swap(x, y), y -= x * (a / b);
  return d;
}

0x40 同余

OI-wiki-线性同余方程

同余是数论的一个基本理论，是很巧妙的工具，它使人们能够用等式的形式简洁地描述整除关系。相关内容有欧拉定理、费马小定理、扩欧、乘法逆元、线性同余方程、中国剩余定理等等。

0x41 同余的定义

• 同余的定义：设 \(m\) 为正整数，\(a\) 和 \(b\) 都为整数，若 \(m \mid (a-b)\)，则称 \(a\) 和 \(b\) 模 \(m\) 同余。
  • 记作 \(a \equiv b \pmod{m}\)。
  • 同样也不用考虑 \(a\) 和 \(b\) 的正负，其实就是要带个绝对值。
• 剩余系：一个模 \(m\) 完全剩余系是一个整数的集合，使得每个整数都与此集合中的一个整数模 \(m\) 同余，例如 \(\left[0,1,2 \ldots m-1 \right]\) 就是模 \(m\) 完全剩余系，称为模 \(m\) 最小非负剩余的集合，剩余系在线性同余方程中有应用。

0x42 同余的定理及性质

首先，\(a,b,c,d,m\) 均为整数。

\(a \equiv b \pmod{m}\) 当且仅当 \(a \bmod m = b \bmod m\)。

把同余式转成等式，即 \(a = b + km\)，\(k\) 为整数，这说明了同余方程与线性丢番图方程的关系。

设 \(m\) 为正整数，则模 \(m\) 有以下性质：

1. 自反性：\(a \equiv a \pmod{m}\)
2. 对称性：若 \(a \equiv b \pmod{m}\)，则 \(b \equiv a \pmod{m}\)
3. 传递性：若 \(a \equiv b \pmod{m}\)、\(b \equiv c \pmod{m}\)，则 \(a \equiv c \pmod{m}\)

同余具有可加可减可乘可乘方性，若 \(a \equiv b \pmod{m}\)、\(c \equiv d \pmod{m}\)，则：

1. 可加性：\(a + c \equiv b + c \pmod{m}\)，甚至 \(a + c \equiv b + d \pmod{m}\)。
2. 可减性：\(a - c \equiv b - c \pmod{m}\)，甚至 \(a - c \equiv b - d \pmod{m}\)。
3. 可乘性：\(ac \equiv bc \pmod{m}\)，甚至 \(ac \equiv bd \pmod{m}\)。
4. 同样不存在可除性，除法取模需要逆元。
5. 同余的幂(可乘方性)：对于任意正整数 \(k\)，\(a^k \equiv b^k \pmod{m}\)

0x43 一元线性同余方程

一元线性同余方程，即给定 \(a,b,m\)，求整数 \(x\) 满足：\(ax \equiv b \pmod{m}\)

研究这个有啥用？\(ax \equiv b \pmod{m}\) 表示 \(ax - b\) 是 \(m\) 的倍数，设为 \(-y\) 倍，则有 \(ax + my = b\)，这就是二元线性丢番图方程。。。(胡言乱语)

0x44 乘法逆元

模板题：P3811 【模板】模意义下的乘法逆元。

乘法逆元主要有三种求法：扩欧、费马小定理、递推预处理。

0x45 扩欧

P1082 [NOIP2012 提高组] 同余方程

• 优点：可以求出 \(m\) 不为质数时的同余方程解。

• 缺点：和费马小定理差不多。

\(ax\equiv 1\pmod m\)，转为 \(ax+bm = 1\)，先求出特解 \(x_0\)，则通解为 \(x=x_0+mn\)，最小整数解就是 \(((x_0 \mod m) + m) \mod m\)。

#include <iostream>

using namespace std;
using ll = long long;

ll x, y, z, w;

void exgcd (ll x, ll y, ll &z, ll &w) {
  if (!y) {
    z = 1, w = 0;
    return ;
  }
  exgcd(y, x % y, w, z), w -= x / y * z;
}

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> x >> y;
  exgcd(x, y, z, w);
  cout << (z % y + y) % y;
  return 0;
}

费马小定理

• 优点：复杂度为 \(O(\log m)\)，处理较少元素逆元十分迅速。

• 缺点：当元素个数来到更高数量级时就不行了，或者 \(m\) 不为质数。

费马小定理，大致就是说 \(x^{m-1} \equiv 1 \pmod{m}\)，那么可以推出 \(\frac{1}{x}\equiv x^{m-2} \pmod{m}\)。

用快速幂处理即可。

递推预处理

• 优点：当需要处理元素在一个 \(O(n)\) 能够处理的范围内时，可以快速求出它们的逆元。

• 缺点：当元素很大时无能为力，或者 \(m\) 不为质数。

证明自己翻书，代码如下：

const int N = 1e5 + 10;

int inv[N];

inv[1] = 1;

for (int i = 2; i <= n; i++) {
  inv[i] = 1ll * (m - m / i) * inv[m % i] % m;
}

0x60 欧拉函数

欧拉函数(Euler's totient function)，即 \(\varphi(n)=\sum\limits_{1\leqslant i\leqslant n}(\gcd(i,n)=1)\)，当 \(n\) 为质数时明显有 \(\varphi(n)=n-1\)。

0x61 性质

1. 欧拉函数是积性函数，即当 \(\gcd(a,b)=1\) 时，\(\varphi(a\times b)=\varphi(a)\times\varphi(b)\)。
2. \(n=\sum\limits_{1\leqslant i\leqslant n \& i \mid n} \varphi(i)\)，详细证明见 OI-wiki。
3. 详细见 OI-wiki。

0x62 欧拉定理

有个正整数 \(m\)，和一个整数 \(a\)，若 \(\gcd(a,m)=1\)，则有 \(a^{\varphi(m)} \equiv 1 \pmod m\)。

0x63 求 \(1\sim n\) 的欧拉函数值

可以在进行欧拉筛的同时计算出每个数的欧拉函数值。

// pri 记录的是质数，phi 记录的是欧拉函数值
f[1] = 1;
for (int i = 2; i <= n; i++) {
  if (!f[i]) {
    pri[++cnt] = i, phi[i] = i - 1;
  }
  for (int j = 1; j <= cnt && i * pri[j] <= n; j++) {
    f[pri[j] * i] = 1, phi[pri[j] * i] = phi[i] * (pri[j] - bool(i % pri[j]));
    if (i % pri[j] == 0) {
      break;
    }
  }
}

0xE0 随手记

0xE1

给出四条边，如何判断是否能够组成梯形。

换句话说，就是梯形的四条边之间有什么关系。

结论：两腰和 > 两底差，两腰差 < 两底差

0xE2 海伦公式

百度百科链接

简单来说，就是给出三角形三边长度 \(a\)、\(b\) 和 \(c\)，求三角形面积的一个公式。

令 \(p = \frac{a+b+c}{2}\)，那么三角形面积就是 \(\sqrt{p\times(p-a)\times(p-b)\times(p-c)}\)

组合数学

排列组合

OI-wiki Link

排列组合是组合数学的基础，排列就是取出部分数字进行排序，组合就是不考虑顺序。

排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。

加法、乘法原理

加法原理：一个东西有 \(n\) 类办法，第 \(i\) 类办法分 \(a_i\) 种，总共就有 \(\sum\limits_{1\leqslant i \leqslant n}a_i\) 种。

乘法原理：一个东西有 \(n\) 个步骤，第 \(i\) 步有 \(a_i\) 种方法，总共就有 \(\prod\limits_{1\leqslant i \leqslant n} a_i\) 种。

排列数与组合数

排列数，代表的是从 \(n\) 个数中任选 \(m\) 个元素在考虑顺序的情况下有多少种情况。

排列数的公式：\(A_n^m=n\times (n-1)\times (n-2)\cdots \times(n-m+1)=\frac{n!}{(n-m)!}\)。

组合数也差不多，但是不考虑顺序。

组合数的公式：\(\begin{pmatrix}n\\m\end{pmatrix}=C_n^m= \frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}\)。

tips:组合数也被称为「二项式系数」。

组合数求解-帕斯卡公式

\(C_n^m=C_n^{m-1}+C_{n-1}^{m-1}\)。

组合数求解-预处理逆元

#include <bits/stdc++.h>
 
using namespace std;
 
const int N = 2e5 + 10, mod = 1e9 + 7;
 
int n, inv[N], x[N], f[N], a, b;
 
int C (int a, int b) {
  return 1ll * f[a] * x[b] % mod * x[a - b] % mod;
}
 
int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  inv[1] = x[0] = f[0] = 1;
  for (int i = 2; i <= 2e5; i++) {
    inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
  }
  for (int i = 1; i <= 2e5; i++) {
    x[i] = 1ll * x[i - 1] * inv[i] % mod, f[i] = 1ll * f[i - 1] * i % mod;
  }
  return 0;
}

二项式定理

\((x+y)^n=\sum\limits_{i=0}\limits^{n} C_n^i x ^{n-i}y^i\)。

卢卡斯定理

卢卡斯定理可以求大数的 \(C_n^m \mod p\)。

对于非负整数 \(n,m\)，\(C_n^m \equiv C_{n\mod p}^{m\mod p}\times C_{\frac{n}{p}}^{\frac{m}{p}} \pmod p\)。

递归实现即可。

int lucas (int n, int m) {
  return (!m ? 1 : 1ll * lucas(n / mod, m / mod) * C(n % mod, m % mod) % mod);
}

多重集排列

有一个多重集，元素种类为 \(n\)，第 \(i\) 个元素有 \(a_i\) 个。

那么多重集的 \(n\) 排列数为 \(\frac{n!}{\prod\limits_{1\leqslant i\leqslant n} a_i}\)。

多重集的 \(r\) 组合数就是 \(C_{n - 1}^{r+n-1}\)。

抽屉(鸽巢)原理

OI-wiki Link

鸽巢(the pigeonhole principle)原理，通常用于求解一些比较极端的情况。

最基础：如果有 \(n+1\) 个物品放入 \(n\) 个抽屉里，至少有 \(1\) 个抽屉至少有 \(2\) 个物品(反证法)。

进阶：如果有 \(k\) 个物品放入 \(n\) 个抽屉里，至少有 \(1\) 个抽屉至少有 \(\left\lceil \frac{k}{n} \right\rceil\)。

容斥原理

OI-wiki Link

容斥原理的思想大致就是在求总量时，可以先不管重不重复，求出总和后再减去重复部分。

二元容斥：\(|A\cup B|=|A|+|B|-|A\cap B|\)。

三元容斥：\(|A\cup B \cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B \cap C|\)。

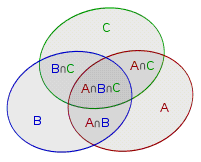
把它推广一下就是我们熟知的容斥原理了。

卡特兰数 Catalan

OI-wiki Link

卡特兰数 \(H_n\) 可以求解以下问题：

• 长度为 \(2n\) 的合法括号序列的个数。
• 在圆上选择 \(2n\) 个点，将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的方法数。
• ......

求解式：

1. \(H_i=\frac{C_{2n}^n}{n+1}\)。
2. \(H_i=\begin{cases} \sum\limits_{0\leqslant j < i} H_j\times H_{i-j-1}&i>0\\ 0&i=0\end{cases}\)。
3. \(H_i=\begin{cases} \frac{4n-2}{n+1}\times H_{i-1} &i>0\\ 0&i=0\end{cases}\)。

$$\texttt{栈}$$

栈(stack)，一种后进先出(last in first out，LIFO)的数据结构，主要有三种操作：压入一个元素到栈顶(push(x))，弹出栈顶的元素(pop())，访问栈顶元素(top())，当然也有询问大小(size())和返回是否为空(empty())。

注：后进先出指的是在当前容器内后进来的先出。

最初的最初：实现一个基本的栈

OI-wiki Link

由于三个操作都只与栈顶有关，所以可以用数组轻松实现。

int stk[N], top;

void Pop () { // 弹出栈顶
  top--;
}

void Push (int x) { // 将元素压入栈
  stk[++top] = x;
}

int Top () { // 返回栈顶元素
  return stk[top];
}

int Size () { // 返回栈的大小
  return top;
}

bool Empty () { // 如果栈为空返回 1，否则返回 0
  return !top;
}

同时 C with STL(c++) 也附赠了一个 STL 容器 stack<元素类型> 容器名;

需要头文件 #include <stack>。

它的成员函数如下：stack<int> stk;

• 元素访问
  • stk.top() 返回栈顶。
• 修改
  • stk.push(x) 将 \(x\) 压入栈顶。
  • stk.pop() 弹出栈顶。
• 容量
  • stk.empty() 返回是否为空。
  • stk.size() 返回元素数量。

废柴的进阶：双端栈

顾名思义，等同于双端队列，见下文。

一个有用的进阶：单调栈

OI-wiki Link

单调栈，顾名思义，就是满足单调性的栈。

假设现在有一个存储整数的单调栈，满足从栈顶往下数都是单调递增的。

初始状态：\([0,11,45,81]\)。

如果要压入整数 \(14\)，为了保证单调性，要将两个比 \(14\) 小的数弹出，再压入整数 \(14\)，此时栈中元素为 \([14,45,81]\)。

const int N = 2e5 + 10;

int stk[N], top;

void Pop () { // 弹出栈顶
  top--;
}

void Push (int x) { // 将元素压入栈
  while (top && stk[top] <= x) {
    Pop();
  }
  stk[++top] = x;
}

int Top () { // 返回栈顶元素
  return stk[top];
}

int Size () { // 返回栈的大小
  return top;
}

bool Empty () { // 如果栈为空返回 1，否则返回 0
  return !top;
}

由于每个元素最多只会入栈出栈各一次，所以复杂度为 \(O(n)\) (\(n\) 为元素数量)。

习题

• P5788 【模板】单调栈
• P1901 发射站

$$\texttt{队列}$$

队列(queue)，一种先进先出(first in first out，FIFO)的数据结构，它满足先入队列的元素一定先出队列(双端队列除外)。

最初的最初：实现一个基本的队列

OI-wiki Link

主要是四种操作：压入一个元素到队尾(push(x))，弹出队头的元素(pop())，访问队头元素(front())，访问队尾元素(back())，当然也有询问大小(size())和返回是否为空(empty())。

一般不建议手写，比较容易出锅，比起来 STL 真是个好东西，STL 队列 queue<元素类型> 容器名;。

需要头文件 #include <queue>。

它的成员函数如下：queue<int> q;

• 元素访问
  • q.front() 返回队头元素。
  • q.back() 返回队尾元素。
• 修改
  • q.push_back(x) 将 \(x\) 压入队尾。
  • q.pop_front() 弹出队头。
• 容量
  • q.empty() 返回是否为空。
  • q.size() 返回元素数量。

一个进阶：双端队列

OI-wiki Link

比起普通的队列，双端队列将 \(2\) 种压入弹出升级为了 \(4\) 种！

STL 也提供了双端队列，头文件没变。

deque<元素类型> 容器名;

假设现在 deque<int> dq;，那么四种压入弹出分别为：

• dq.push_front(x) 将 \(x\) 压入队头。
• dq.push_back(x) 将 \(x\) 压入队尾。
• dq.pop_front() 弹出队头。
• dq.pop_back() 弹出队尾。

别的成员函数没变，值得一提的是它支持随机化访问！即你可以用 dq[0] 来访问队头。

不过常数比 queue 大，非必要情况下不建议使用。

另一个进阶：单调队列

OI-wiki Link

先放一道例题：P1886 滑动窗口 /【模板】单调队列。

大致题意就是给定一个长度为 \(n\) 的整数数组 \(a\)，要对于每个长度为 \(k\) 的区间求出区间的最大最小值。

从前往后处理，为了维持单调性，那么当你要压入元素时，你可以用类似单调栈的方式，将那些不优的元素先弹出，再压入元素。

不同的是，这里区间长度为 \(k\)，那么“过期”元素则需要特殊处理。很明显单调队列中的元素下标也是单调递增的，直接重复弹出队头即可。

由于涉及到了队尾弹出，可以使用双端队列。

细节有些，但不多。

习题

• P2698 Flowerpot S

$$\texttt{倍增}$$

OI-wiki Link

倍增，顾名思义就是成倍增长。可以在 \(O(n\log n)\) 的预处理后将 \(O(n)\) 的询问降低到 \(O(\log n)\)，大大降低时间复杂度。

倍增主要运用于 RMQ 问题或 LCA 问题。

思想

举个例子，假设现在给定了一个长度为 \(n(n\leqslant 10^5)\) 的整数数组 \(a\)，你需要回答 \(q(q\leqslant 10^5)\) 组询问，每次询问给定 \(l,r\)，求 \(\max\limits_{l\leqslant i \leqslant r} \{a_i\}\)。

暴力找？\(O(n\times q)\) 爆炸了，这时就需要使用倍增来处理了。为了将询问复杂度降低到对数级别，则需先预处理。对于每个 \(i\)，预处理出 \([i,i],[i-2^0,i],[i-2^1,i],[i-2^2,i]\cdots [i-2^{\log n},i]\) 的最大值(如果左端点小于 \(0\) 则当 \(0\) 处理)。

具体实现

令 mx[i][j] 表示 \(\max\limits_{\max(1,i-2^j+1)\leqslant k \leqslant i} \{a_i\}\)，则有 mx[i][0] = a[i]，当 j 为正数时 mx[i][j] = max(mx[i][j - 1], mx[max(0, i - (1 << (j - 1)))][j - 1])。

询问处理

对于一段区间 \([l,r]\)，可以将长度 \(r-l+1\) 做一次二进制拆分，按位从高到低枚举，如果当前位(第 \(i\) 位)为 \(1\)，则 mx[r][i] 会产生共享，统计进去，再右移 \(r\) 至 \(r-2^i\)。

时间复杂度：\(O(\log n)\)。

除了维护区间 RMQ，还可以 \(O(\log n)\) 维护树上两点间的 LCA。

首先预处理出每个节点的 \(2^0,2^1,2^2\cdots 2^{\log n}\) 级祖先，令 fa[i][j] 表示 \(i\) 的 \(2^j\) 级祖先，则可以先搜索找出每个节点的 \(2^0\) 级祖先，然后就有当 j 为正数时，fa[i][j] = fa[fa[i][j - 1]][j - 1]。

当要求 \(x\) 和 \(y\) 的 LCA 时，首先让两个点跳到同一深度，令 h[i] 表示节点 \(i\) 的深度，且 h[x] <= h[y]，那么就先让 \(y\) 跳到 \(y\) 的 h[y] - h[x] 级祖先处，如果此时 \(x=y\)，那么直接返回 \(x\) 即可。

否则，按位(\(i\))从大到小枚举，如果 fa[x][i] != fa[y][i]，那么 x = fa[x][i], y = fa[y][i]，最后返回 fa[x][0] 即可。

$$\texttt{ST 表}$$

OI-wiki Link

ST 表是用于解决可重复贡献问题的数据结构(例如解决区间 RMQ 或区间 gcd 等问题)，基于倍增思想。

还是用上面的例子，求一段区间的最大值。倍增可以 \(O(\log n)\) 解决，而 ST 表则更是大优化，可以 \(O(1)\) 处理询问！

思想

首先和倍增一样预处理。

由于 RMQ 问题是可重复共献问题(即只要处理的区间在询问区间范围内且包含了范围内的所有可贡献元素，即使重复计算也不影响答案)，所以可以考虑将其拆分成两个区间处理，只要这两个区间的并集为 \([l,l+1\cdots r]\)。

处理

首先预处理出 \(1\sim n\) 的 \(\log\)，\(Log_i=\begin{cases} 0&i=1\\Log_{\left\lfloor \frac{i}{2}+1\right\rfloor}&i\geqslant 2 \end{cases}\)。

那么就好办了，对于一个区间 \([l,r]\) 最大值就是 max(mx[r][Log[r - l + 1]], mx[l + (1 << Log[r - l + 1]) - 1][Log[r - l + 1]])。

询问 \(O(1)\) 处理。

P3865 【模板】ST 表

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m, mx[N][20], l, r, Log[N];

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m, Log[0] = -1;
  for (int i = 1; i <= n; i++) {
    cin >> mx[i][0], Log[i] = Log[i / 2] + 1;
  }
  for (int i = 1; i <= 16; i++) {
    for (int j = (1 << i); j <= n; j++) {
      mx[j][i] = max(mx[j][i - 1], mx[j - (1 << (i - 1))][i - 1]);
    }
  }
  for (int i = 1; i <= m; i++) {
    cin >> l >> r;
    cout << max(mx[r][Log[r - l + 1]], mx[l + (1 << Log[r - l + 1]) - 1][Log[r - l + 1]]) << '\n';
  }
  return 0;
}

并查集

基本的并查集

OI-wiki Link

并查集，一种用于管理元素所属集合的数据结构，形如一片森林，同一棵树内的元素所属同一集合，不同树内的元素不属于同一集合。

将并查集拆分一下。并，合并；查，查询；集，处理的是集合相关内容。

所以并查集一共有两种操作：合并两元素对应集合、查询某元素所属集合(查询它所在树的树根)。

对于每个元素，需要记录它的父亲，用于寻找树根。

如果需要的话，可以记录它的子树大小，一般只有树根需要记录。

初始化

初始时，每个元素都是一棵树，它们自然没有父亲。

如果要记录子树大小的话，则需把它们初始都赋值为 \(1\)。

查询

当我们要查询一个元素 \(x\) 所属集合时，我们需要一路往上跳，直到跳到 \(x\) 所属树的树根，这个元素也就是 \(x\) 所属的集合。

int Find (int x) { // 查询 x 所属集合
  return (fa[x] ? Find(fa[x]) : x); // 如果当前节点还有父亲节点，那么就往上跳，否则返回当前节点
}

合并

假如现在要合并两个元素 \(x,y\) 的所属集合，那么只要先找到两棵树的树根，再任选一个点连向另一点即可。

如果仅仅是告诉你两个元素 \(x,y\) 所属同一集合，那么还需判断 \(x,y\) 是否所属不同集合，否则可能会导致死递归。

void merge (int x, int y) { // 合并 x, y 所属集合
  x = Find(x), y = Find(y); // 找到树根
  if (x != y) { // 只有 x, y 所属不同集合时才能合并
    fa[x] = y; // 连接
  }
}

并查集时间复杂度优化

合并的复杂度在于查询，除了查询以外只用 \(O(1)\)，那么查询的复杂度呢？

很明显，我们可以利用合并构造出一种形如链状的并查集，那么在查询时复杂度仍然可以达到 \(O(n)\)，并没有达到优化的效果。

那么就要提到合并和查询的优化了。

路径压缩

路径压缩，顾名思义就是把一长条路径给压缩，从而降低时间。

int Find (int x) { // 查询 x 所属集合
  return (fa[x] ? fa[x] = Find(fa[x]) : x); // 如果当前节点还有父亲节点，那么就往上跳，否则返回当前节点
  // 路径压缩，每次往上跳时都把 fa[x] 更新为树根。
}

启发式合并

当合并两个集合时，集合的大小会影响到后续操作，为了在一定程度上优化时间复杂度，可以选择把节点数少的集合连向节点数多的集合，也可以把深度较小的集合连向深度较大的集合。

// 按节点数启发式合并
void merge (int x, int y) { // 合并 x, y 所属集合
  x = Find(x), y = Find(y); // 找到树根
  if (x != y) { // 只有 x, y 所属不同集合时才能合并
    if (sz[x] > sz[y]) { // 启发式合并
      swap(x, y);
    }
    fa[x] = y, sz[y] += sz[x]; // 连接
  }
}

时间复杂度比较玄学，可以自行 bdfs 或者参考 OI-wiki。

一般来说路径压缩后的并查集已经不怕 T，但是启发式合并 + 路径压缩后是 \(O(\alpha(n)\times n)\)，其中 \(\alpha(n)\) 为反阿克曼函数，是一个增长十分缓慢的函数，一般题目里可以将 \(\alpha(n)\) 视为 \(5\) 左右的一个常数，是完全不可能 T 的。

带权并查集

OI-wiki Link

就是在维护普通并查集的同时维护每个节点连接向它的父亲的边权，路径压缩时记得要更新为一段路径的边权。

例题：P1196 [NOI2002] 银河英雄传说。

种类并查集

不要问我为啥没有 OI-wiki Link，因为 OI-wiki 里甚至没有这玩意。

与普通并查集十分相像，主要就是把一个元素分为几个类，可以直接开多个并查集维护。

例题：P2024 [NOI2001] 食物链。

在这道题里，由于不确定每个动物的种类，则将其分类讨论，分为三类，处理时多一点细节。

$$\texttt{线段树}$$

OI-wiki Link

线段树是一种支持修改、用于维护区间信息的数据结构，可以在 \(O(\log n)\) 的复杂度下求出一个大小为 \(n\) 的数组的区间信息（如区间和、区间最大值等），也可以在同样时间复杂度下实现单点修改和区间修改等操作。

静态区间和可以使用前缀和优化，但如果有修改操作呢？当你更新一个点 \(i\) 时，前缀和数组中 \(i,i+1,i+2\cdots n\) 都要更新，时间复杂度来到了 \(O(n)\)，无法接受，这时候我们就需要使用线段树。

基本结构

假设现在有一个大小为 \(5\) 的数组 \(a = \{10,11,12,13,14 \}\)，用线段树维护区间和如下：

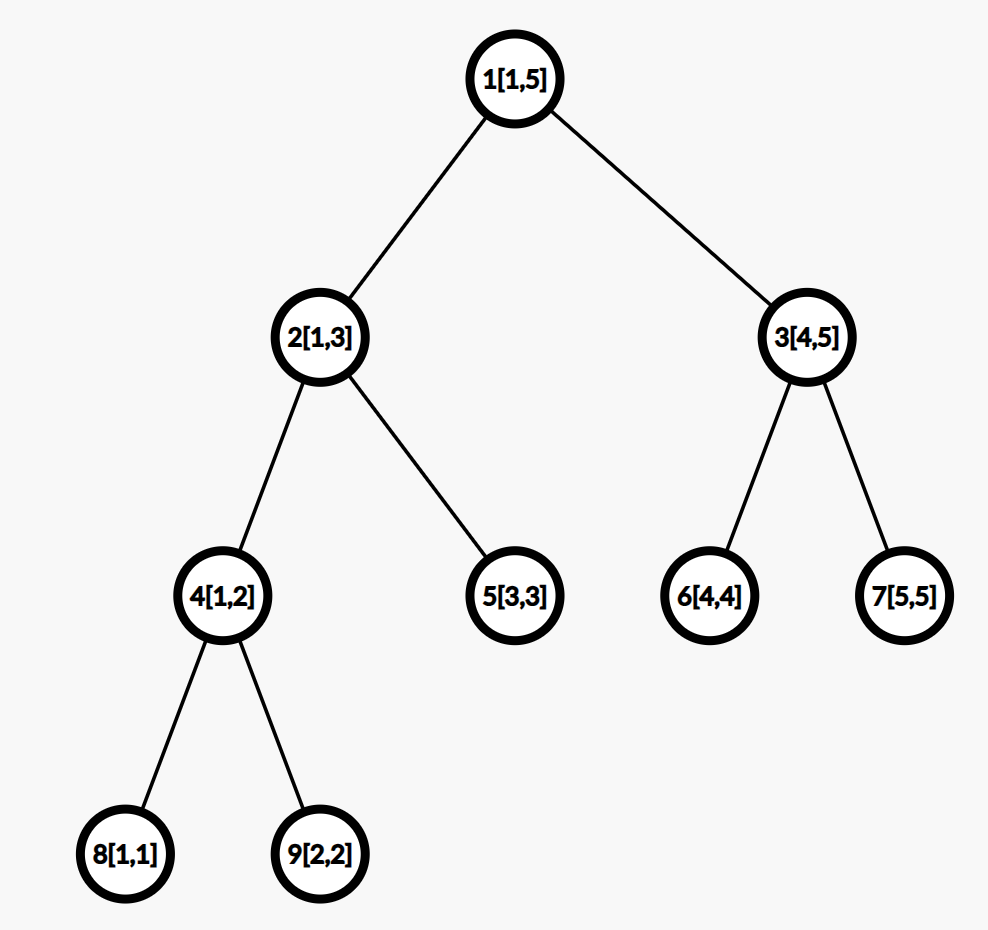
大致思想：最初有一个区间 \([1,n]\)，对于一个出现在线段树的区间 \([l,r] (l \ne r)\)，将其分为左右两个区间 \([l, \frac{l + r}{2}]\) 和 \([\frac{l + r}{2} + 1, r]\)，各自处理，然后再结合左右区间更新区间信息。

区间肯定不能 \(O(n^2)\) 记录，为了防止区间编号冲突，可以把编号为 \(i\) 的节点的左儿子编号设为 \(2 \times i\)，右儿子编号设为 \(2 \times i + 1\)。

空间分析

现在有一个问题：编号最大为多少？

通过观察，容易发现线段树深度为 \(\left\lceil \log n \right\rceil\)，则编号最大为 \(2 ^ {\left\lceil \log n \right\rceil + 1} - 1\)，稍加计算可得编号不超过 \(4 \times n\)。

详细证明请右转 OI-wiki。

Code

int n, a[N], tr[4 * N];

// Make Tree 建树
void MT (int id, int l, int r) { // 当前节点编号为 id，区间范围 [l, r]
  if (l == r) {
    tr[id] = a[l];
    return ;
  }
  int mid = (l + r) >> 1;
  MT(id * 2, l, mid), MT(id * 2 + 1, mid + 1, r);
  tr[id] = tr[id * 2] + tr[id * 2 + 1];
}

复杂度 \(O(n)\)。

区间查询

对于上面的例子，我们现在需要查询某些区间的和。

如果是查询 \([1,5]\)，很明显，\(d_1\) 即可，可要是要求 \([2,5]\) 的怎么办呢?

既然 \([2,5]\) 并没有直接出现，那么考虑将其分为若干个出现在线段树上的区间进行求解。

大致做法

• 如果当前遍历到的区间 \(id[l,r]\) 被查询区间完全包含，那么可以直接计算当前区间对答案的贡献，即 \(d_{id}\)。
• 如果当前遍历到的区间 \(id[l,r]\) 与查询区间无交集，直接 return ;
• 否则，将其分为左右两个区间进行查询，即查询 \(id \times 2 [l, \frac{l + r}{2}]\) 和 \(id \times 2 + 1 [\frac{l + r}{2} + 1, r]\)。

时间复杂度分析

做法了解了，接下来就是分析时间复杂度了。

我们可以把 \([l,r]\) 分成 \([l,l], [l+1,l+1], [l+2,l+2], \cdots [r-1,r-1],[r,r]\)，尽量合并。

由于查询是一段连续区间，所以当你把所有可以合并的区间都合并之后，线段树每层最多只会有两个区间，时间复杂度为 \(O(\log n)\)。

Code

int qry;

// Query 查询
void Query (int id, int l, int r, int x, int y) { // 查询区间 [x, y]
  if (l >= x && r <= y) { // 当前区间被查询区间完全包含
    qry += tr[id];
    return ;
  }
  if (l > y || r < x) { // 当前区间与查询区间无交集
    return ;
  }
  int mid = (l + r) >> 1;
  Query(id * 2, l, mid, x, y), Query(id * 2 + 1, mid + 1, r, x, y);
}

单点修改

继续使用上面的例子，如果我们要修改 \(a_2\) 为 \(13\)，该如何更新线段树呢？

如图，当你找到区间 \([2,2]\) 对应线段树上哪个节点时，你可以直接将其修改，然后再从下往上重新更新线段树每个节点即可，时间复杂度 \(O(\log n)\)。

如何寻找区间对应节点呢？当我们考虑到一个包含修改目标的区间 \(id[l,r](l \ne r)\)，很明显左右两个区间有且仅有一个区间包含修改目标，继续寻找即可，时间复杂度 \(O(\log n)\)。

总时间复杂度为 \(O(\log n)\)。

Code

// modify 单点修改
void modify (int id, int l, int r, int x, int y) { // 将 a[x] 修改为 y
  if (l == r) { // 找到修改目标
    tr[id] = y; // 直接修改
    return ;
  }
  int mid = (l + r) >> 1;
  if (mid >= x) { // 修改目标在左半区间
    modify(id * 2, l, mid, x, y);
  } else { // 修改目标在右半区间
    modify(id * 2 + 1, mid + 1, r, x, y);
  }
  tr[id] = tr[id * 2] + tr[id * 2 + 1]; // 重新更新
}

区间修改与懒标记

单点修改解决，然后就是区间修改。如果对于区间内每个元素都进行一次单点修改，时间复杂度无法接受，需要使用懒标记。

懒标记 lazy tag

懒标记，顾名思义就是一种十分懒惰的标记，用于临时记录区间操作对于当前节点对应范围造成的影响，当它要访问它的左右儿子时，需要将懒标记下传并更新左右儿子的节点信息，懒标记初始为 \(0\)。

引入懒标记，初始状态：

懒标记下传 Code

int lzy[4 * N];

// 将 id[l, r] 的懒标记下传
void pushdown (int id, int l, int r) {
  int mid = (l + r) >> 1;
  tr[id * 2] += lzy[id] * (mid - l + 1); // 左区间 tr 更新
  tr[id * 2 + 1] += lzy[id] * (r - mid); // 右区间 tr 更新
  lzy[id * 2] += lzy[id]; // 左区间 lazy tag 更新
  lzy[id * 2 + 1] += lzy[id]; // 右区间 lazy tag 更新
  lzy[id] = 0; // 清空当前节点 lazy tag
}

有了懒标记，我们就可以实现 \(O(\log n)\) 的区间修改了。

操作类似区间查询(将区间 \([x,y]\) 每个元素增加 \(z\))：

• 如果当前遍历到的区间 \(id[l,r]\) 被修改区间完全包含，则更新当前节点的懒标记(\(t_{id} += z\))和答案(\(d_{id} += z \times (r - l + 1)\))。
• 如果当前遍历到的区间 \(id[l,r]\) 与修改区间无交集，直接 return ;
• 否则，将其分为左右两个区间各自修改，即修改 \(id \times 2 [l, \frac{l + r}{2}]\) 和 \(id \times 2 + 1 [\frac{l + r}{2} + 1, r]\)。

区间修改（加） Code

// modify 区间修改-加
void modify (int id, int l, int r, int x, int y, int z) { // 将 a[x ~ y] 每个元素加 z
  if (l >= x && r <= y) { // 当前区间被修改区间完全包含
    lzy[id] += z, tr[id] += (r - l + 1) * z;
    return ;
  }
  if (l > y || r < x) { // 当前区间与修改区间无交集
    return ;
  }
  int mid = (l + r) >> 1;
  pushdown(id, l, r); // 懒标记下传
  modify(id * 2, l, mid, x, y, z), modify(id * 2 + 1, mid + 1, r, x, y, z);
  tr[id] = tr[id * 2] + tr[id * 2 + 1]; // 重新更新当前节点
}

区间修改（赋值） Code

容易发现，一个数只与最后一次对它的赋值操作有关。所以懒标记下传与更新需要一点点的更改。

// 将 id[l, r] 的懒标记下传
void pushdown (int id, int l, int r) {
  int mid = (l + r) >> 1;
  tr[id * 2] = lzy[id] * (mid - l + 1); // 左区间 tr 更新
  tr[id * 2 + 1] = lzy[id] * (r - mid); // 右区间 tr 更新
  lzy[id * 2] = lzy[id]; // 左区间 lazy tag 更新
  lzy[id * 2 + 1] = lzy[id]; // 右区间 lazy tag 更新
  lzy[id] = 0; // 清空当前节点 lazy tag
}

// modify 区间修改-赋值
void modify (int id, int l, int r, int x, int y, int z) { // 将 a[x ~ y] 每个元素赋值为 z
  if (l >= x && r <= y) { // 当前区间被修改区间完全包含
    lzy[id] = z, tr[id] = (r - l + 1) * z;
    return ;
  }
  if (l > y || r < x) { // 当前区间与修改区间无交集
    return ;
  }
  int mid = (l + r) >> 1;
  pushdown(id, l, r); // 懒标记下传
  modify(id * 2, l, mid, x, y, z), modify(id * 2 + 1, mid + 1, r, x, y, z);
  tr[id] = tr[id * 2] + tr[id * 2 + 1]; // 重新更新当前节点
}

优化

1. 叶子节点没有儿子，所以懒标记不用下传到叶子节点。
2. 根据儿子更新当前节点的操作可以写一个函数 pushup，增加代码可读性。
3. 标记永久化：在确定懒标记不会发生溢出的情况下，可以选择不清空懒标记，只计算对答案的贡献(用处不大，主要用于可持久化数据结构)。
4. 动态开点：左右儿子不设为 \(id \times 2\) 和 \(id \times 2 + 1\)，而是设为线段树中没有出现的最小 \(id\)。线段树第一层节点数最多为 \(1\)，第二层最多为 \(2\)，第三层最多为 \(4\)，依次类推，可以计算出节点数量最多为 \(2 \times n - 1\)，可以节省空间。

$$\texttt{树状数组}$$

OI-wiki Link

树状数组，是一种用于维护单点修改和区间查询的数据结构。

一些要求

普通树状数组要求维护的信息和运算满足结合律且可差分(具有逆运算)，包括加法、乘法、异或等。

注意：

• 模意义下乘法若要可差分，需要保证每个元素都存在逆元。
• 区间极值、最大公因数等无法用普通树状数组维护(但有办法解决，详见 OI-wiki)。

初步感知

假设现在有一个数组 \(a\)，如果我们要求 \(\sum\limits_{1\leqslant i \leqslant 7} a_i\)，很明显是算 \(a_1\) 到 \(a_7\) 这七个数的和，那如果令 \(A = a_1 + a_2 + a_3 + a_4\)，\(B = a_5 + a_6\)，\(C = a_7\)，那么你肯定会说答案就是 \(A+B+C\)。

这就是树状数组，可以在预处理出一些区间的和之后，把一段前缀化为不超过 \(\log n\) 个预处理过的区间，以 \(O(\log n)\) 的方式求出前缀和。

上图中的 \(c\) 数组用于存储数组 \(a\) 的某些区间的和，可以发现 \(c_i\) 的右端点为 \(i\)，可左端点呢？

区间管辖范围

树状数组规定：右端点为 \(i\) 的区间的大小为 \(2^{k_i}\)，其中 \(k\) 表示 \(i\) 在二进制表示下最低位的 \(1\) 的位数(最低位位数为 \(0\))。

令 lowbit(i) 为 \(2^{k_i}\)，那么根据位运算知识，我们可以知道 lowbit(x) = x & (-x)，这个东西和原、反、补码有关，这里就不详说了，具体可以看 OI-wiki。

构建树状数组

强调：必须确保维护的信息是可差分的，例如求区间和，而区间极值则不可以用树状数组进行维护。

现在给定一个大小为 \(n\) 的数组 \(a\)，要维护区间和，怎么构建树状数组呢？

可以想到一种比较简单的方法：对于每个 \(1\leqslant i \leqslant n\)，求一下 \(\sum\limits_{i-lowbit(i)+1\leqslant j \leqslant i} a_i\)，那么时间复杂度为多少呢？

通过找规律，可以发现这个的时间复杂度在 \(n=10^7\) 也只是来到了 \(12\times n\) 左右，甚至达不到 \(n\log n\)，也就是说，在正常情况下是完全可以通过的。

验证 Code

#include <iostream>

using namespace std;

int lowbit (int x) {
  return x & -x;
}

int n, ans;

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++) {
    ans += lowbit(i);
  }
  cout << ans;
  return 0;
}

Code

void MT () {
  for (int i = 1; i <= n; i++) {
    for (int j = i - lowbit(i) + 1; j <= i; j++) { // 统计范围内的整数和
      tr[i] += a[j];
    }
  }
}

当然如果你提前用前缀和进行预处理的话，可以直接 \(O(n)\) 解决。

区间查询

举个例子，现在要求区间 \([3, 5]\) 的和，那么就可以将其分为两个前缀 \([1,5]\) 和 \([1,2]\) 分别进行求解，然后做差(前缀和思想)。

根据区间管辖范围，我们可以轻松地推出前缀和的求法：函数 Query(x) 求解的是前缀 \([1,x]\) 的和，先算上以 \(x\) 结尾的区间和 \(c_x\)，求解范围为 \([x - lowbit(x) + 1,x]\)，也就是说还差 \([1,x - lowbit(x)]\) 没有求解，也就是 Query(x - lowbit(x))，如果现在 x = 0，即已将前缀完全求解，那么直接返回 \(0\) 即可。

Code

inline int lowbit (int x) {
  return x & -x; // 位运算求 lowbit
}

int n, tr[N]; // tr 就是 c 数组

int Query (int x) {
  return (x ? tr[x] + Query(x - lowbit(x)) : 0); // 分类讨论
}

单点修改

树状数组の一些性质

令 \(l_x\) 为 \(x - lowbit(x) + 1\)。

1. 对于任意 \(x \leqslant y\)，要么 \(l_y > x\)，要么 \(l_y \leqslant l_x\)。
2. 对于任意 \(x\)，有 \(l_{x+lowbit(x)} \leqslant l_x\)。
3. 对于任意 \(x < y < x + lowbit(x)\)，有 \(l_y > x\)。

详细证明见 OI-wiki。

假设现在要将 \(a_x\) 加上 \(y\)。

为了快速更新 \(c\)，我们只需要更新所有包含 \(x\) 的 \(c\) 即可。

根据如上几个性质，可以推出更新方法：当 \(c_a\) 包含 \(x\) 时，更新 \(c_a\)，并更新 \(c_{a + lowbit(a)}\)，以此类推，直到 \(a > n\)，此时也就是更新完毕了，很明显 \(c_x\) 是一定包含 \(x\) 的。

Code

void modify (int x, int y) { // 单点修改
  if (x > n) { // 更新完毕
    return ; // 返回
  }
  tr[x] += y, modify(x + lowbit(x), y); // 更新
}

复杂度 \(O(\log n)\)。

区间修改

开两个树状数组，利用查分维护即可。

$$\texttt{字符串哈希}$$

OI-wiki Link

字符串哈希，将字符串映射为一个整数，利用这个整数快速地判断两个字符串是否相等。

令函数 \(f(s)\) 为字符串 \(s\) 映射后的整数。

主要性质

假设现在有两个字符串 \(s\) 和 \(t\)。

• 当 \(f(s) \ne f(t)\) 时，\(s\) 一定与 \(t\) 不同。
• 当 \(f(s) = f(t)\) 时，\(s\) 不一定与 \(t\) 相同。

当 \(f(s) = f(t)\) 且 \(s \ne t\) 时，我们称发生了哈希冲突。

大致思想

首先设定进制数 \(P\) 和模数 \(mod\) (模数必须为质数)以及单个字符的映射规则，要求每个单个字符映射后的数不会冲突，通常可以使用其 ASCII 码或者整体偏移一定值，但得确保每个字符映射后的数都要严格小于 \(P\)。

然后将字符串看作一个 \(P\) 进制数，每个位上的数都是其对应位置上的字符经过映射后得到的数，高位在左。

将其转为十进制，记得这个十进制数要模 \(mod\)。

const int P = 131, mod = 1e9 + 7; // p 为进制数，mod 为模数
const int N = 1e5 + 10;

string s;
int n, hsh[N], p[N];

int id (char c) { // 单个字符映射规则
  return c - 'a';
}

int get_Hash (int l, int r) { // 返回子串 [l, r] 的哈希值
  int sum = 0;
  for (int i = l; i <= r; i++) {
    sum = (1ll * sum * P + id(s[i])) % mod; // 转十进制
  }
  return sum;
}

哈希冲突

当有 \(n\) 个不同的字符串时，不发生哈希冲突的概率是 \(\frac{mod \times (mod - 1) \times (mod - 2) \cdots (mod - n + 1)}{mod^n}\)。

当 \(mod = 10^9+7\) 时，经过测试，我们可以发现：

• 当 \(n = 10^2\) 时，概率大致为 \(99.999505001212170588950622907021\%\)。
• 当 \(n = 10^3\) 时，概率大致为 \(99.950062456651772569132113899215\%\)。
• 当 \(n = 10^4\) 时，概率大致为 \(95.123402247659835488397678249228\%\)。
• 当 \(n = 5\times 10^4\) 时，概率大致为 \(28.650599316946955379668306174157\%\)。
• 当 \(n = 6\times 10^4\) 时，概率大致为 \(16.529789848427975192568691042982\%\)。
• 当 \(n = 7\times 10^4\) 时，概率大致为 \(8.629167509240295731162218376142\%\)。
• 当 \(n = 10^5\) 时，概率大致为 \(0.673716114763418643374601169592\%\)。
• 当 \(n = 2 \times 10^5\) 时，概率大致为 \(0.000000205861313426543109296943\%\)。
• 当 \(n = 5 \times 10^5\)，概率已经小于了 \(10^{-30}\)！

当 \(n\) 来到 \(2 \times 10^5\) 及以上时，不出现哈希冲突的概率已经很小了，也就是说模数设为 \(10^9+7\) 顶多也就是解决 \(n \leqslant 6 \times 10^4\) 的题，当 \(n\) 更大时几乎是必然出现哈希冲突，则需要考虑更大的模数。

当 \(mod = 10^{18}+3\) 时(这是个质数)，经过测试，我们可以惊喜的发现：

• 当 \(n = 10^4\) 时，概率大致为 \(99.999999994999513598095339239613\%\)。
• 当 \(n = 10^5\) 时，概率大致为 \(99.999999499995059201512201396689\%\)。
• 当 \(n = 10^6\) 时，概率大致为 \(99.999949999962680605332387973050\%\)，趋近于 \(100\%\)！
• 当 \(n = 10^7\) 时(以下为研究所需，正常题目不可能出这么大的数据范围)，概率大致为 \(99.995000124497913132062473784423\%\)，仍然趋近于 \(100\%\)！
• 当 \(n = 10^8\) 时，概率大致为 \(99.501247914276431954941695701145\%\)，也是几乎不会出现哈希冲突。
• 当 \(n = 10^9\) 时，概率大致为 \(60.653065930827893892981345080884\%\)。

也就是说，当模数设为 \(10^{18}+3\) 时，正常题目几乎不可能出现哈希冲突(如果出现了，那么恭喜你，你可以去买彩票了！)。

注意，当模数设为 \(10^{18}+3\) 时，使用 long long 计算可能会导致溢出，需要用 __int128 来计算，直接强制类型转换((__int128)1)即可。

using ll = long long;

// p 为进制数，mod 为模数
const int P = 131;
const ll mod = 1e18 + 3;
const int N = 1e5 + 10;

string s;
int n;
ll hsh[N], p[N];

int id (char c) { // 单个字符映射规则
  return c - 'a';
}

ll get_Hash (int l, int r) { // 返回子串 [l, r] 的哈希值
  ll sum = 0;
  for (int i = l; i <= r; i++) {
    sum = ((__int128)1 * sum * P + id(s[i])) % mod; // 转十进制
  }
  return sum;
}

附：测试代码如下：

#include <bits/stdc++.h>

using namespace std;

const int mod = 1e9 + 7;
// const long long mod = 1e18 + 3;

long double x = 1;
int n;

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++) {
    x = x * (mod + 1 - i) / mod;
  }
  cout << fixed << setprecision(32) << x;
  return 0;
}

快速求子串哈希值

可我们发现，上面的代码中求子串的哈希值仍然是 \(O(n)\) 的，这和暴力判断没有区别，怎么优化呢？

再观察一下，当字符串不会改变时，可以考虑预处理。

using ll = long long;

// p 为进制数，mod 为模数
const int P = 131;
const ll mod = 1e18 + 3;

const int N = 1e5 + 10;

string s;
int n;
ll hsh[N]; // 存储前缀哈希值

int id (char c) { // 单个字符映射规则
  return c - 'a';
}

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> s, n = s.size(), s = " " + s, p[0] = 1;
  for (int i = 1; i <= n; i++) { // 预处理前缀哈希值
    hsh[i] = ((__int128)1 * hsh[i - 1] * P + id(s[i])) % mod; // 转为十进制数，hsh[i] 表示前 i 位哈希后的结果
  }
  return 0;
}

若要求子串 \([l,r]\) 的哈希值，则使用类似于前缀和的求法，公式：\(hsh_r - hsh_{l-1} \times P^{r-l+1}\)。

可以发现 \(r-l+1\leqslant n\)，则可以在预处理前缀哈希值的同时处理 \(P\) 的 \(0 \sim n\) 次方在模 \(mod\) 意义下的值。

for (int i = 1; i <= n; i++) { // 预处理前缀哈希值
  p[i] = (__int128)1 * p[i - 1] * P % mod; // p[i] 表示 P 的 i 次方 % mod 的值
  hsh[i] = ((__int128)1 * hsh[i - 1] * P + id(s[i])) % mod; // 转为十进制数，hsh[i] 表示前 i 位哈希后的结果
}

记得减法取模的细节。

ll Hash (int l, int r) { // 返回子串 [l, r] 哈希值
  return (hsh[r] + mod - (__int128)1 * hsh[l - 1] * p[r - l + 1] % mod) % mod;
}

附：生日悖论

百度百科 Link

生日悖论，指的是随机选出 \(23\) 个或更多人，出现至少两个人生日相同的概率高于 \(50\%\)。

由于这点反人类直觉，所以被称为“生日悖论”。

计算式子很类似哈希冲突，所以提到哈希往往都会提到生日悖论。

验证代码：

#include <bits/stdc++.h>

using namespace std;

long double x = 1;
int n;

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++) {
    x = x * (366 - i) / 365;
  }
  cout << fixed << setprecision(32) << x; // 随机选择 n 个人，两两生日不同的概率
  return 0;
}

$$\texttt{哈希表}$$

详见 OI Wiki。

可以用 map。

OI-wiki Link

要提到 KMP 算法，首先得提到字符串相关知识。

KMP

字符串相关

概念

• 前缀/后缀：这个很容易理解。
• 真前缀/真后缀：就是非原串的前缀/后缀。
• 子串：从原串中选取连续的一段就是一个子串，空串也算子串。
  • 任何子串都是一个前缀的后缀/一个后缀的前缀。
• 周期：当满足 \(s_i=s_{i+p}(1\leqslant i \leqslant |s|-x)\) 时，\(x\) 是 \(s\) 的周期。
• Border：当一个字符串 \(t\)，既是 \(s\) 的前缀，又是 \(s\) 的后缀时，\(t\) 就是 \(s\) 的一个 Border。

性质

• 当一个字符串 \(t\) 为 \(s\) 的 Border 时，\(|s|-|t|\) 为 \(s\) 的一个周期。
• Border 具有传递性，即当 \(x\) 为 \(y\) 的 Border、\(y\) 为 \(z\) 的 Border 时，必然有 \(x\) 为 \(z\) 的 Border。
• Border 传递性 \(2\)：当 \(x\) 为 \(z\) 的 Border、\(y\) 为 \(z\) 的 Border 时，必然有 \(x\) 为 \(y\) 的 Border。

字符串匹配

模板：P3375 【模板】KMP。

令 \(pre(s,i)\) 表示 \(s\) 的长度为 \(i\) 的前缀，\(suf(s,i)\) 表示 \(s\) 的长度为 \(i\) 的后缀。

给定两个字符串 \(s\) 和 \(t\)(\(1\leqslant |s|,|t|\leqslant 10^5\))，现在要查询 \(s\) 在 \(t\) 中的出现位置有哪些。

暴力匹配 \(O(|s| \times |t|)\)，爆炸。

我们拿两个指针 \(i,j\) 表示 \(s[1\cdots i]\) 与 \(t[j-i+1\cdots j]\) 完全相同，\(j\) 在 \(1\sim |t|\) 循环，同时 \(i\) 相应变化，始终满足 KMP 性质：\(suf(pre(t,j),i)=pre(s,i)\)(\(i\) 越大越好)。

在更新时 \(i,j\) 时：

• 若 \(s_{i+1}=t_{j+1}\)，则各自后移，i++, j++;，当 \(i=n\) 时，\(s\) 已经完全匹配，可以推出它的起始位置等。
• 否则，右移 \(j\)，调整 \(i\)，使得 \(suf(pre(t,j),i)=pre(s,i)\) 仍然满足，那么该如何调整呢？

Next[] 失配数组

在发生不匹配时，我们需要调整 \(i\)，这个可以通过预处理来解决，通常定义为 Next 数组，有时也叫 fail 数组(失配数组)。

nxt[i] = max{k | pre(s, k) = suf(pre(s, i), k)}，即 \(pre(s,i)\) 的最长 Border。

若 \(pre(s,k)\) 为 \(pre(s,i)\) 的 Border，则有：

• \(pre(s,k-1)\) 为 \(pre(s,i-1)\) 的 Border。
• \(s_k=s_i\)。

求解方法

假设 \(pre(s,i-1)\) 的所有 Border 长度为 $k_1 > k_2 > k3 \cdots $。

• 需要找到其中最大的 \(k\) 使得 \(s_{k+1} = s_i\)。
• 此时 nxt[i] = k + 1(即 \(pre(s,i)\) 的最长 Border)。

根据定义和 Border 的传递性，\(pre(s,i-1)\) 的所有 Border 其实就是 \(nxt_{i-1},nxt_{nxt_{i-1}}\cdots\)

• 求 \(nxt_i\) 就是 \(k=nxt_{i-1}\) 开始检查 \(s_{k+1}=s_j\)是否成立，不成立就一直往前找 Next。\(k= nxt_k\) 然后重复上述判断(找到满足条件的最长 Border)。

Code

void get_fail () {
  for (int i = 2, j = 0; i <= m; i++) {
    while (j && s[i] != s[j + 1]) {
      j = nxt[j];
    }
    if (s[i] == s[j + 1]) {
      j++;
    }
    nxt[i] = j;
  }
}

求完了失配数组，剩下就好办了。

KMP Code

for (int i = 1, j = 0; i <= n; i++) {
  while (j && t[i] != s[j + 1]) {
    j = nxt[j];
  }
  if (t[i] == s[j + 1]) {
    j++;
  }
  if (j == m) {
    cout << i - j + 1 << '\n';
  }
}

模板完整代码

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n, m, nxt[N];
string s, t;

void get_fail () {
  for (int i = 2, j = 0; i <= m; i++) {
    while (j && s[i] != s[j + 1]) {
      j = nxt[j];
    }
    if (s[i] == s[j + 1]) {
      j++;
    }
    nxt[i] = j;
  }
}

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> t >> s, n = t.size(), m = s.size(), s = " " + s, t = " " + t;
  get_fail();
  for (int i = 1, j = 0; i <= n; i++) {
    while (j && t[i] != s[j + 1]) {
      j = nxt[j];
    }
    if (t[i] == s[j + 1]) {
      j++;
    }
    if (j == m) {
      cout << i - j + 1 << '\n';
    }
  }
  for (int i = 1; i <= m; i++) {
    cout << nxt[i] << ' ';
  }
  return 0;
}

时间复杂度：\(O(|s|+|t|)\)。

字符串的周期

性质里有，而字符串 \(s\) 的最小周期则是 \(|s|-nxt_{|s|}\)。

失配树

顾名思义，就是将 \(i(1\leqslant i \leqslant n)\) 连向 \(nxt_i\) 所形成的树。

这棵树有什么用呢？树上的两个节点 \(x,y\) 的 LCA 就是 \(pre(s,x)\) 和 \(pre(s,y)\) 的最长公共 Border。

而一个节点 \(i\) 的祖先则都是 \(pre(s,i)\) 的 Border。

例题：P5829 【模板】失配树 | P3435 [POI2006] OKR-Periods of Words。

字典树

引入

字典树(trie)，顾名思义就是在字典上建树用于维护字符串的前缀相关内容。

在字典树中，每条边都是一个字符，从根节点到任意一个节点都可以代表一个字符串(例如 \(1 \rightarrow 2 \rightarrow 6 \rightarrow 11\) 就代表了 \(aba\))。

模板题：P8306 【模板】字典树。

结构

大致结构如上图。

对于一个节点，它需要记录它的儿子的编号，必要时还需要记录这个节点在加入字符串的操作中访问了几次(即有几个字符串有这个前缀)。

令 trie[i][j] 表示节点 \(i\) 走一条边权为 \(j\) 后到达的节点编号，如果不存在则设为 \(0\)。

边权则使用离散化思想处理，例如 0~25 分别对应着 a~z，26~51 表示 A~Z 等等。

加入字符串

令 id(char c) 表示 \(c\) 在离散化后的整数。

在处理新加入的字符串 \(s\) 时，从前往后枚举每一位，假设当前节点为 \(x\)，处理到了字符串的第 \(i\) 位，那么如果 trie[x][id(s[i])] 为 \(0\)，则新增一个节点，将 \(x\) 设为新增节点编号，否则 x = trie[x][id(s[i])]。

int id (char c) { // 字符映射规则
  return (c >= 'a' && c <= 'z' ? c - 'a' : (c >= 'A' && c <= 'Z' ? 26 + c - 'A' : 52 + c - '0'));
}

void Insert (string s) { // 加入一个字符串
  int now = 0; // 当前节点编号
  for (int i = 0; i < s.size(); i++) {
    if (!trie[now][id(s[i])]) { // 没有对应节点
      trie[now][id(s[i])] = ++cnt; // 新建节点
    }
    now = trie[now][id(s[i])], sum[now]++; // 跳过去，统计数量 + 1
  }
}

查询字符串

与加入差不多，但当没有对应节点时不应该新建节点，而是直接返回 \(0\)。

int Query (string s) { // 查询有多少个字符串以 s 为前缀
  int now = 0; // 当前节点编号
  for (int i = 0; i < s.size(); i++) {
    if (!trie[now][id(s[i])]) { // 没有对应节点
      return 0; // 直接返回
    }
    now = trie[now][id(s[i])]; // 跳过去
  }
  return sum[now]; // 返回结果
}

模板题 Code

#include <iostream>

using namespace std;

const int N = 3e6 + 10;

int t, trie[N][65], sum[N], cnt, n, q;
string s;

int id (char c) { // 字符映射规则
  return (c >= 'a' && c <= 'z' ? c - 'a' : (c >= 'A' && c <= 'Z' ? 26 + c - 'A' : 52 + c - '0'));
}

void Insert (string s) { // 加入一个字符串
  int now = 0; // 当前节点编号
  for (int i = 0; i < s.size(); i++) {
    if (!trie[now][id(s[i])]) { // 没有对应节点
      trie[now][id(s[i])] = ++cnt; // 新建节点
    }
    now = trie[now][id(s[i])], sum[now]++; // 跳过去，统计数量 + 1
  }
}

int Query (string s) { // 查询有多少个字符串以 s 为前缀
  int now = 0; // 当前节点编号
  for (int i = 0; i < s.size(); i++) {
    if (!trie[now][id(s[i])]) { // 没有对应节点
      return 0; // 直接返回
    }
    now = trie[now][id(s[i])]; // 跳过去
  }
  return sum[now]; // 返回结果
}

void Solve () {
  cnt = 0;
  cin >> n >> q;
  for (int i = 1; i <= n; i++) {
    cin >> s;
    Insert(s);
  }
  while (q--) {
    cin >> s;
    cout << Query(s) << '\n';
  }
  for (int i = 0; i <= cnt; i++) {
    for (int j = 0; j < 62; j++) {
      trie[i][j] = 0;
    }
    sum[i] = 0;
  }
}

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  for (cin >> t; t; t--) {
    Solve();
  }
  return 0;
}

应用

• 检索字符串，例如模板题。
• 01 字典树，但是不会。
• AC 自动姬，但是也不会。

$$\texttt{矩阵运算}$$

众所周知，数是可以进行加减乘除的，那矩阵为啥不可以呢？

假设现在我们有两个矩阵 \(A\) 和 \(B\)，矩阵大小分别为 \(n \times m\) 和 \(x \times y\)，矩阵元素对 \(mod\) 取模。

const int N = 110, mod = 1e9 + 7; // 矩阵大小和模数

struct matrix {
  int a[N][N], n, m; // 存储矩阵和矩阵大小
} ;

基本运算

矩阵加法

令 \(A + B = C\)。

要求：\(n = x\) 并且 \(m = y\)。

其实很简单，就是一一对应着加就行，即对于 \(1\leqslant i \leqslant n, 1\leqslant j \leqslant m\)，\(C_{i, j} = A_{i, j} + B_{i, j}\)。

所以 \(C\) 的大小为 \(n \times m\)，矩阵减法同。

性质

• 交换律：明显满足，即 \(A + B = B + A\)。
• 结合律：明显满足，即 \(A + B + C = A + (B + C)\)。

单位矩阵

明显，就是一个大小为 \(n \times m\) 的全 \(0\) 矩阵。

矩阵加法 Code

时间复杂度：\(O(n \times m)\)。

  matrix operator + (matrix y) { // 重载运算符 +
    matrix z;
    z.n = n, z.m = m;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= m; j++) {
        z.a[i][j] = a[i][j] + y.a[i][j];
      }
    }
    return z;
  }

矩阵乘法

令 \(A \times B = C\)。

要求：\(m = x\)。

公式：对于 \(1 \leqslant i \leqslant n, 1 \leqslant j \leqslant y\):

似乎看起来没啥用？因为它是在某些特定方面可以进行时间优化(例如用 \(O(8 \log n)\) 的时间复杂度求出斐波那契数列的第 \(n\) 项)，所以一般就是把它和其他知识点捆绑起来(例如矩阵乘法优化 dp 等)，单独拎出来出的题目很少(大多都是板子)。

性质

• 交换律：不满足！
  • 若 \(n = y\)，交换以后还能乘法，但矩阵大小会变为 \(m \times x\)，与原矩乘后答案不同。
  • 当然也有可能 \(n \neq y\)，这样交换以后连矩乘的基本要求都无法满足。
• 结合律：满足，设还有一个矩阵 \(C\)，大小为 \(y \times z\)，\(A \times B \times C = D\)，则 \(D\) 大小为 \(n \times z\)，而 \(A \times (B \times C) = A \times E(\texttt{大小为} x \times z) = D\)。
• 分配律：明显满足，设还有一个矩阵 \(C\)，大小为 \(y \times z\)，即 \(A \times (B + C) = A \times B + A \times C\)。

单位矩阵

Link

提到矩乘，就不得不提到它的单位矩阵。

单位矩阵定义：若这个矩阵乘任意一个矩阵 \(C\)，得到的结果都等于 \(C\)，则这个矩阵为单位矩阵。

观察式子，容易推出：当一个大小为 \(n \times n\) 的矩阵除了主对角线(从左上到右下)以外的数为 \(1\)，其他都为 \(0\) 时，它就是一个可以作为所有大小为 \(n \times m\) 的矩阵的单位矩阵。

时间复杂度：\(O(x \times y)\)。

  void Clear (int x, int y, int f) { // 把矩阵大小设为 x * y，矩阵元素都为 f
    n = x, m = y;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= m; j++) {
        a[i][j] = f;
      }
    }
  }
  void Unit (int x, int y) { // 构造单位矩阵
    Clear(x, y, 0); // 先清空
    for (int i = 1; i <= n; i++) {
      a[i][i] = 1; // 只有主对角线为 1
    }
  }

矩阵乘法 Code

时间复杂度：\(O(n \times m \times y)\)。

  matrix operator * (matrix y) { // 重载运算符 *
    matrix z;
    z.n = n, z.m = y.m;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= y.m; j++) {
        z.a[i][j] = 0;
        for (int k = 1; k <= m; k++) {
          z.a[i][j] = (z.a[i][j] + 1ll * a[i][k] * y.a[k][j] % mod) % mod; // 套公式
        }
      }
    }
    return z;
  }

矩阵除法

令 \(\frac{A}{B} = C\)。

要求：同矩阵乘法。

由于浮点数不可以取模，数里面除法取模等于乘上除数的逆，所以矩阵除法同矩阵除法，不过是把 \(B_{i, j}\) 变成 \(B_{i, j}\) 在模 \(mod\) 意义下的逆。

矩乘与它的特殊运算和应用

P3390 矩乘快速幂

给定一个矩阵 \(A\)，大小为 \(n \times m\)，一个指数 \(k\) 和一个模数 \(mod\)，求 \(A^k\ \%\ mod\)。

要求：矩阵的大小必须为 \(n \times n\)。

既然矩乘有结合律，那么就可以考虑使用类似于整数快速幂的方法以 \(O(\log k)\) 的方式求出 \(A^k\)，由于一次矩阵乘法需要 \(O(n^3)\)，所以总时间复杂度为 \(O(n ^ 3 \log k)\)。

矩乘快速幂 Code

时间复杂度：\(O(n ^ 3 \log k)\)。

matrix qmod (matrix x, ll y) { // 矩阵乘法快速幂
  matrix sum;
  sum.Unit(x.n, x.m); // 初始化为单位矩阵
  while (y) {
    if (y & 1) {
      sum = sum * x;
    }
    x = x * x, y >>= 1;
  }
  return sum;
}

P1349 广义斐波那契数列

P1962 斐波那契数列

广义的斐波那契数列是指形如 \(a_n=p\times a_{n-1}+q\times a_{n-2}\) 的数列。

今给定数列的两系数 \(p\) 和 \(q\)，以及数列的最前两项 \(a_1\) 和 $ a_2$，另给出两个整数 \(n\) 和 \(m\)，试求数列的第 \(n\) 项 \(a_n \bmod m\)。

令 \(F_i\) 表示当前情况下斐波那契数列第 \(i\) 项的值。

观察一下，把相邻两项构成一个矩阵，即要从 \(f_i = \begin{bmatrix}F_i,F_{i - 1}\end{bmatrix}\) 通过操作变为 \(f_{i + 1} = \begin{bmatrix}F_{i + 1},F_i\end{bmatrix} = \begin{bmatrix}p \times F_i + q \times F_{i - 1},F_i\end{bmatrix}\)，考虑用矩乘完成。

要能与 \(\begin{bmatrix}F_i,F_{i - 1}\end{bmatrix}\) 做矩乘，就需要一个大小为 \(2 \times k\) 的矩阵，又因为矩乘之后的矩阵仍然大小为 \(1 \times 2\)，所以 \(k = 2\)，即要求一个矩阵 \(A = \begin{bmatrix}a,b\\c,d\end{bmatrix}\)，使得 \(A \times f_i = f_{i + 1}\)。

套入公式，就是要求 \(\begin{cases}a\times F_i + c \times F_{i - 1} = p \times F_i + q \times F_{i - 1}\\b\times F_i + d \times F_{i - 1}=F_i\end{cases}\)，可以推出 \(\begin{cases}a=p\\b=1\\c=q\\d=0\end{cases}\)，现在要求 \(F_n\)，初始矩阵为\(\begin{bmatrix}a_2,a_1\end{bmatrix}\)，每次乘矩阵 \(A = \begin{bmatrix}p,1\\q,0\end{bmatrix}\) 后都会使矩阵两项下标加 \(1\)，特判 \(n = 1\) 的情况(答案为 \(a_1\))，那么答案就是 \(\begin{bmatrix}a_2,a_1\end{bmatrix} \times A^{n - 2}\) 取第一个元素即可，需要矩阵乘法快速幂。

普通的其实就相当于 \(a_1=a_2=p=q=1\)。

Code

  matrix c, d;
  int n, mod;
  c.Clear(2, 2, 0), d.Clear(1, 2, 0);
  cin >> c.a[1][1] >> c.a[2][1] >> d.a[1][2] >> d.a[1][1] >> n >> mod;
  if (n == 1) {
    cout << d.a[1][2];
    return 0;
  }
  c.a[1][2] = 1, d = d * qmod(c, n - 2);
  cout << d.a[1][1];

完整代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

const int N = 110, mod = 1e9 + 7; // 矩阵大小和模数

struct matrix {
  int a[N][N], n, m; // 存储矩阵和矩阵大小
  void Clear (int x, int y, int f) { // 把矩阵大小设为 x * y，矩阵元素都为 f
    n = x, m = y;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= m; j++) {
        a[i][j] = f;
      }
    }
  }
  void Unit (int x, int y) { // 构造单位矩阵
    Clear(x, y, 0); // 先清空
    for (int i = 1; i <= n; i++) {
      a[i][i] = 1; // 只有主对角线为 1
    }
  }
  matrix operator + (matrix y) { // 重载运算符 +
    matrix z;
    z.n = n, z.m = m;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= m; j++) {
        z.a[i][j] = a[i][j] + y.a[i][j];
      }
    }
    return z;
  }
  matrix operator * (matrix y) { // 重载运算符 *
    matrix z;
    z.n = n, z.m = y.m;
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= y.m; j++) {
        z.a[i][j] = 0;
        for (int k = 1; k <= m; k++) {
          z.a[i][j] = (z.a[i][j] + 1ll * a[i][k] * y.a[k][j] % mod) % mod; // 套公式
        }
      }
    }
    return z;
  }
} ;

matrix qmod (matrix x, ll y) { // 矩阵乘法快速幂
  matrix sum;
  sum.Unit(x.n, x.m); // 初始化为单位矩阵
  while (y) {
    if (y & 1) {
      sum = sum * x;
    }
    x = x * x, y >>= 1;
  }
  return sum;
}

int min () {
  ios::sync_with_stdio(0), cin.tie(0);
  return 0;
}

本栏目推荐文章
• [python]沪深龙虎榜数据导入通达信的自选板块，并标注于K线图上
• 2023年主线板块：数字经济+（产业化）+（价值化）+（数字化）
• uniapp登录板块封装(旧接口getUserInfo)
• HTML5 小米浮动和手机购买板块
• R语言Copula模型分析股票市场板块相关性结构|附代码数据
• 第二十八篇——一通达信板块函数INSUM、BLOCKSETNUM简介以及应用（从零起步编写通达信指标公式系列）
• 八大板块总结合集！
• TDengine 3.1.0.0 版本成功发布，涉及五大板块功能更新！
• 技术篇33：板块及股票均是周期循环下资金运行的载体/周五复盘，尾盘又见小冰点数据
• python爬虫学习小记——lxml板块

板块线图 龙虎榜 板块 数据 先见 大盘 板块 信号 减速器 风向 概率 板块 技术篇 冰点 载体 板块 平面几何 几何 板块 平面 blocksetnum公式 函数 板块 爬虫 小记 板块python 减速器 零部件 板块 重点 getuserinfo板块 接口uniapp 板块 强度 行业2023