向量的外积

定义

定义1 2个向量\(\bm{a},\bm{b}\)的外积（记作\(\bm{a}\times \bm{b}\)）仍然是一个向量，其长度规定为：

\[|\bm{a}\times \bm{b}|=|\bm{a}||\bm{b}|\sin<\bm{a},\bm{b}> \]

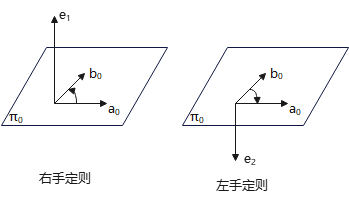
方向规定（符合右手规则）：与\(\bm{a}, \bm{b}\)均垂直，且向量\(\bm{a},\bm{b},\bm{a}\times\bm{b}\)形成向量系——右手四指从\(\bm{a}\)弯向\(\bm{b}\)（转角<π）时，拇指的指向就是\(\bm{a}\times\bm{b}\)的方向.

如果\(\bm{a},\bm{b}\)中有一个为0，则\(\bm{a}\times \bm{b}=0\).

推论1 \(\bm{a}\times\bm{b}=0\)的充要条件：\(\bm{a},\bm{b}\)共线.

证明：

\[a\times b = 0 \Leftrightarrow |a||b|\sin\braket{a,b}=0 \Leftrightarrow |a|=0,|b|=0或\sin\braket{a,b}=0\Leftrightarrow a,b共线 \]

几何意义

当\(\bm{a},\bm{b}\)不共线时，\(|\bm{a}\times \bm{b}|\)表示以\(\bm{a},\bm{b}\)为邻边的平行四边形的面积.

\(|\bm{a}\times \bm{b}|\)的方向符合右手定则（下图垂直向量\(\bm{a}.\bm{b}\)所确定平面向上）：

外积的运算规律

命题1 若向量\(\bm{a}\neq 0\)，则\(\bm{a}\times\bm{b}=\bm{a}\times\bm{b_2}\)，其中\(\bm{b_2}\)是\(\bm{b}\)沿方向\(\bm{a}\)的外射影.
注：外射影指\(\bm{b}\)在\(\bm{a}\)垂直方向的投影，模为\(|\bm{b}|\sin<\bm{a},\bm{b}>\).

证：\(\bm{b}=\bm{b_1}+\bm{b_2}\)，其中\(\bm{b_1}//\bm{a},\bm{b_2}⊥\bm{a}\)，而投影直角三角形中，\(\bm{b}|\sin<\bm{a},\bm{b}>\)
而

\[|\bm{a}\times\bm{b}|=|\bm{a}||\bm{b}|\sin<\bm{a},\bm{b}>=|\bm{a}||\bm{b_2}|=|\bm{a}\times\bm{b_2}| \]

又\(\bm{a}\times\bm{b}\)与\(\bm{a}\times\bm{b_2}\)同向
∴\(\bm{a}\times\bm{b}=\bm{a}\times\bm{b_2}\).

命题2 设\(\bm{e}\)是单位向量，\(\bm{b}⊥\bm{e}\)，则\(\bm{e}\times\bm{b}\)等于\(\bm{b}\)按右手螺旋规则绕\(\bm{e}\)旋转90°得到向量\(\bm{b}'\).

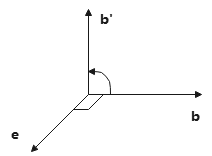
证明：
\(|\bm{e}\times\bm{b}|=|\bm{e}||\bm{b}|\sin<\bm{e},\bm{b}>=|\bm{b}|\)
∵\(\bm{b}'\)由\(\bm{b}\)旋转90°得到
∴\(|\bm{b}|=|\bm{b}'|=|\bm{e}\times \bm{b}|\)，\(\bm{b'}⊥\bm{b}, \bm{b'}⊥\bm{e}\).
∴\(\bm{b'}//\bm{e}\times \bm{b}\)
又由上图知，\(\bm{b}', \bm{e}\times \bm{b}\)同向
∴\(\bm{b}'=\bm{e}\times\bm{b}\)

推论2 若\([O;\bm{e_1},\bm{e_1},\bm{e_2},\bm{e_3}]\)为右手直角坐标系，则有

\[\bm{e_1}\times\bm{e_2}=\bm{e_3},\bm{e_2}\times\bm{e_3}=\bm{e_1},\bm{e_3}\times\bm{e_1}=\bm{e_2} \]

定理1 外积运算规律：对于任意向量\(\bm{a},\bm{b},\bm{c}\)，任意实数λ，有
1）\(\bm{a}\times\bm{b}=-\bm{b}\times{a}\)（反交规律）；
2）\((\lambda \bm{a})\times\bm{b}=\lambda(\bm{a}\times\bm{b})\)；
3）\(\bm{a}\times(\bm{b}+\bm{c})=\bm{a}\times\bm{b}+\bm{a}\times\bm{c}\)（左分配律）
\((\bm{b}+\bm{c})\times\bm{a}=\bm{b}\times\bm{a}+\bm{c}\times\bm{a}\)（右分配律）.

证明：
1）由外积定义可知\(\bm{a}\times \bm{b},\bm{b}\times \bm{a}\)模相等，方向相反，故等式成立.

2） \(|(\lambda \bm{a})\times\bm{b}|= |\lambda\bm{a}||\bm{b}|\sin<\lambda\bm{a},\bm{b}>=|\lambda||\bm{a}||\bm{b}|\sin<\bm{a},\bm{b}>=|\lambda||\bm{a}\times\bm{b}| =|\lambda(\bm{a}\times\bm{b})|\)

\(\lambda>0\)时，\(\lambda \bm{a}, \bm{a}\)同向 => \((\lambda \bm{a})\times\bm{b}\)与\(\lambda(\bm{a}\times\bm{b})\)同向；

\(\lambda<0\)时，等式左边与与\((\bm{a}\times\bm{b})\)反向，而右边也与\((\bm{a}\times\bm{b})\)反向 => 左边与右边同向.

\(\lambda=0\)时，等式显然成立.

3）左分配律，
设\(\bm{a}\)方向单位向量\(\bm{a^0}\)，将向量\(\bm{b},\bm{c}\)分别分解为\(\bm{a^0}\)方向及其垂直方向的2个分量，设\(\bm{b}=\bm{b_1}+\bm{b_2}\)，其中\(\bm{b_1}//\bm{a^0}⊥\bm{b_2}, \bm{c_1}//\bm{a^0}⊥\bm{c_2}\).

\[\begin{aligned} 左边&=(|\bm{a}|\bm{a^0)}\times[(\bm{b_1}+\bm{b_2})+(\bm{c_1}+\bm{c_2})]\\ &=|\bm{a}|[\bm{a^0}\times((\bm{b_1}+\bm{c_1})+(\bm{b_2}+\bm{c_2}))]\\ 右边&=|\bm{a}|(\bm{a^0}\times \bm{b_2}+\bm{a^0}\times \bm{c_2}) \end{aligned} \]

由命题1知，对外积有贡献的是向量的外射影. 因此

\[左边=|\bm{a}|[\bm{a^0}\times(\bm{b_2}+\bm{c_2})] \]

\(\bm{a^0}⊥\bm{b_2},\bm{c_2}=>\bm{a^0}⊥\bm{d}(\bm{d}=\bm{b_2}+\bm(c_2))\)

根据命题2，\(\bm{a^0}\times \bm{d}\)等价于\(\bm{d}\)绕\(\bm{a^0}\)向右旋转90°得到的向量\(\bm{d'}\).
同理，
\(\bm{a^0}\times \bm{b_2}\)等价于\(\bm{b_2}\)绕\(\bm{a^0}\)向右旋转90°得到的向量\(\bm{b_2'}\)；
\(\bm{a^0}\times \bm{c_2}\)等价于\(\bm{c_2}\)绕\(\bm{a^0}\)向右旋转90°得到的向量\(\bm{c_2}\).

因此，

\[\begin{aligned} 左边&=|\bm{a}|\bm{d'}\\ 右边&=|\bm{a}|(\bm{b_2'}+\bm{c_2'}) \end{aligned} \]

旋转前，\(\bm{b_2},\bm{c_2},\bm{d}\)形成三角形，旋转后也一定能形成三角形，因此，

\[\bm{d'}=\bm{b_2'}+\bm{c_2'} \]

故左边=右边.

右分配律，

\[\begin{aligned} (\bm{b}+\bm{c})\times \bm{a}&=-\bm{a}\times(\bm{b}+\bm{c})\\ &=-(\bm{a}\times\bm{b}+\bm{a}\times\bm{c})\\ &=\bm{b}\times\bm{a}+\bm{c}\times\bm{a} \end{aligned} \]

计算向量的外积

外积的坐标计算

仿射坐标系\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)下，设\(\bm{a},\bm{b}\)的坐标为\((a_1,a_2,a_3)(b_1,b_2,b_3)\)，则

\[\begin{aligned} \bm{a}\times \bm{b}&=(a_1\bm{e_1}+a_2\bm{e_2}+a_3\bm{e_3})\times (b_1\bm{e_1}+b_2\bm{e_2}+b_3\bm{e_3})\\ &=(a_1b_2-a_2b_1)\bm{e_1}\times \bm{e_2}+(a_3b_1-a_1b_3)\bm{e_3}\times \bm{e_1}+(a_2b_3-a_3b_2)\bm{e_2}\times \bm{e_3} \end{aligned} \]

因此，只要知道基向量的外积，就能求出\(\bm{a}\times \bm{b}\).

右手直角标架下，\(\bm{e_1}\times \bm{e_2}=\bm{e_3},\bm{e_2}\times \bm{e_3}=\bm{e_1},\bm{e_3}\times \bm{e_1}=\bm{e_2}\)
因此，

\[\bm{a}\times \bm{b}=(a_2b_3-a_3b_2)\bm{e_1}+(a_3b_1-a_1b_3)\bm{e_2}+(a_1b_2-a_2b_1) \bm{e_3} \]

外积的坐标表示

定理2 设\(\bm{a},\bm{b}\)在右手直角坐标系中坐标坐标为\((a_1,a_2,a_3)(b_1,b_2,b_3)\)，则\(\bm{a}\times \bm{b}\)的坐标为

\[\begin{pmatrix} \begin{vmatrix} a_2 & b_2\\ a_3 & b_3 \end{vmatrix}, -\begin{vmatrix} a_1 & b_1\\ a_3 & b_3 \end{vmatrix}, \begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix} \end{pmatrix} \]

证明很简单，由上面的坐标计算向量外积即可知. 也可以写成三阶行列式形式：

\[\bm{a}\times \bm{b}=\begin{vmatrix} \bm{e_1} & a_1 & b_1\\ \bm{e_2} & a_2 & b_2\\ \bm{e_3} & a_3 & b_3 \end{vmatrix} \]

tips：按第1列展开可得坐标形式.

向量的混合积

定义

定义2 \(\bm{a}\times\bm{b}\cdot \bm{c}\)称为向量\(\bm{a},\bm{b},\bm{c}\)的混合积.

几何意义

混合积\(\bm{a}\times\bm{b}\cdot \bm{c}\)几何意义是什么？
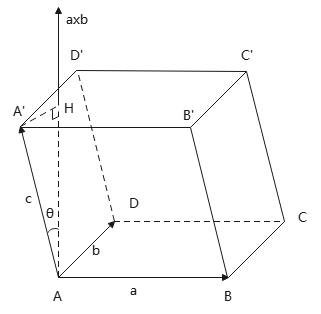
当\(\bm{a},\bm{b}\)不共线时，知外积\(|\bm{a}\times\bm{b}|\)表示\(\bm{a},\bm{b}\)为邻边的平行四边形面积.而\(\bm{a}\times\bm{b}\cdot \bm{c}\)表示以\(\bm{a},\bm{b},\bm{c}\)为棱的平行六面体的体积.

如下图，平行六面体ABCDA'B'C'D'中，
\(S_{ABCD}=|\bm{a}\times\bm{b}|, h=|\bm{c}||\cos \theta| \implies V=S_{ABCD}\cdot h=|\bm{a}\times\bm{b}||\bm{c}||\cos\theta|\)
而θ是向量\(\bm{c},\bm{a}\times\bm{b}\)的夹角
∴\(V=|\bm{a}\times\bm{b}\cdot \bm{c}|\)

当\(\bm{a}\times \bm{b}\cdot \bm{c}>0\)时，θ为锐角，\((\bm{a},\bm{b},\bm{c})\)构成右手系；
当\(\bm{a}\times \bm{b}\cdot \bm{c}=0\)时，θ为直角，\(\bm{a},\bm{b},\bm{c}\)共面；
当\(\bm{a}\times \bm{b}\cdot \bm{c}<0\)时，θ为钝角，\((\bm{a},\bm{b},\bm{c})\)构成左手系.

命题3 3个向量\(\bm{a},\bm{b},\bm{c}\)共面的充要条件：\(\bm{a}\times \bm{b}\cdot c=0\).

证明：由混合积体积意义，即可得证.

常用性质

1）\(\bm{a}\times \bm{b}\cdot \bm{c}=\bm{b}\times \bm{c}\cdot \bm{a}=\bm{c}\times \bm{a}\cdot \bm{b}\)；
2）\(\bm{a}\times \bm{b}\cdot c=\bm{a}\cdot \bm{b}\times \bm{c}\).

证明：
1）∵\(|\bm{a}\times \bm{b}\cdot \bm{c}|,|\bm{b}\times \bm{c}\cdot \bm{a}|,|\bm{c}\times \bm{a}\cdot \bm{b}|\)表示以\(\bm{a},\bm{b},\bm{c}\)为棱的平行六面体体积
∴\(|\bm{a}\times \bm{b}\cdot \bm{c}|=|\bm{b}\times \bm{c}\cdot \bm{a}|=|\bm{c}\times \bm{a}\cdot \bm{b}|\)

如果\((\bm{a},\bm{b},\bm{c})\)为右手系，则\((\bm{b},\bm{c},\bm{a}), (\bm{c},\bm{a},\bm{b})\)均为右手系，即\(\bm{a}\times \bm{b}\cdot \bm{c},\bm{b}\times \bm{c}\cdot \bm{a}, \bm{c}\times \bm{a}\cdot \bm{b}\)结果均>=0；

反之若为左手系，结果均<0；
也就是说，三者同号. 故得证.

2）\(\bm{a}\times\bm{b}\cdot\bm{c}=\bm{b}\times\bm{c}\cdot \bm{a}=(\bm{b}\times\bm{c})\cdot \bm{a}=\bm{a}\cdot (\bm{b}\times\bm{c})=\bm{a}\cdot \bm{b}\times\bm{c}\)

tips: 外积优先级比内积更高，否则内积得到的常数与向量进行外积运算没有意义.

计算向量的混合积

混合积的坐标计算

取仿射标架\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)，设\(\bm{a},\bm{b},\bm{c}\)坐标分别为\((a_1,a_2,a_3),(b_1,b_2,b_3),(c_1,c_2,c_3)\). 则

\[\begin{aligned} \bm{a}\times\bm{b} \cdot \bm{c}&=(a_1,a_2,a_3)\times (b_1,b_2,b_3)\cdot (c_1,c_2,c_3)\\ &=(a_1\bm{e_1}+a_2\bm{e_2}+a_3\bm{e_3})\times (b_1\bm{e_1}+b_2\bm{e_2}+b_3\bm{e_3})\cdot (c_1\bm{e_1}+c_2\bm{e_2}+c_3\bm{e_3})\\ &=[(a_1b_2-a_2b_1)\bm{e_1}\bm{e_2}+(a_3b_1-a_1b_3)\bm{e_3}\times \bm{e_1}+(a_2b_3-a_3b_2)\bm{e_2}\times \bm{e_3}](c_1\bm{e_1}+c_2\bm{e_2}+c_3\bm{e_3})\\ &=[(a_1b_2-a_2b_1)c_3+(a_3b_1-a_1b_3)c_2+(a_2b_3-a_3b_2)c_1]\bm{e_1}\times \bm{e_2}\cdot \bm{e_3}\\ &=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\bm{e_1}\times \bm{e_2} \cdot \bm{e_3} \end{aligned} \]

∵\(\bm{e_1},\bm{e_2},\bm{e_3}\)不共面
∴\(\bm{e_1}\times \bm{e_2} \cdot \bm{e_3}\neq 0\).

定理3 如果\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)为右手直角标架，向量\(\bm{a},\bm{b},\bm{c}\)坐标分别为\((a_1,a_2,a_3),(b_1,b_2,b_3),(c_1,c_2,c_3)\)，则

\[\bm{a}\times\bm{b} \cdot \bm{c}=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix} \]

证明：∵\([O;\bm{e_1},\bm{e_2},\bm{e_3}]\)为右手直角标架
∴\(\bm{e_1}\times\bm{e_2}=\bm{e_3}\)
∴\(\bm{e_1}\times \bm{e_2} \cdot \bm{e_3}=\bm{e_3}\cdot \bm{e_3}=1\)
∴\(\bm{a}\times\bm{b} \cdot \bm{c}=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\bm{e_1}\times \bm{e_2} \cdot \bm{e_3}=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\)

三向量（或四点）共面条件

三向量共面

定理4 设\(\bm{a},\bm{b},\bm{c}\)的仿射坐标\((a_1,a_2,a_3),(b_1,b_2,b_3),(c_1,c_2,c_3)\)，则\(\bm{a},\bm{b},\bm{c}\)共面的充要条件：

\[\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}=0 \]

证明：
由命题3知，3向量共面充要条件：\(\bm{a}\times\bm{b}\cdot \bm{c}=0\)
由上面混合积的坐标计算知，

\[\bm{a}\times\bm{b}\cdot \bm{c}=\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\bm{e_1}\times \bm{e_2} \cdot \bm{e_3} \]

∵\(\bm{e_1},\bm{e_2},\bm{e_3}\)不共面
∴\(\bm{e_1}\times \bm{e_2}\cdot \bm{e_3}\neq 0\)
∴3向量共面充要条件是\(\begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}=0\)

四点共面

推论3 设4个点A，B，C，D的仿射坐标\((x_i,y_i,z_i),i=1,2,3,4\). 则A，B，C，D共面的充要条件：

\[\begin{vmatrix} x_1 & x_2 & x_3 & x_4\\ y_1 & y_2 & y_3 & y_4\\ z_1 & z_2 & z_3 & z_4\\ 1 & 1 & 1 & 1 \end{vmatrix}=0 \]

证明：A，B，C，D共面，即\(\overrightarrow{DA},\overrightarrow{DB},\overrightarrow{DC}\)共面
由三向量共面定理知，充要条件为：

\[\begin{vmatrix} x_1-x_4 & x_2-x_4 & x_3-x_4\\ y_1-y_4 & y_2-y_4 & y_3-y_4\\ z_1-z_4 & z_2-z_4 & z_3-z_4 \end{vmatrix}=0 \]

等式等价于（按最后一行展开）

\[\begin{vmatrix} x_1-x_4 & x_2-x_4 & x_3-x_4 & x_4\\ y_1-y_4 & y_2-y_4 & y_3-y_4 & y_4\\ z_1-z_4 & z_2-z_4 & z_3-z_4 & z_4\\ 0 & 0 & 0 & 1 \end{vmatrix}=0 \]

将行列式前3列都加上最后一列，值不变：

\[\begin{vmatrix} x_1-x_4 & x_2-x_4 & x_3-x_4 & x_4\\ y_1-y_4 & y_2-y_4 & y_3-y_4 & y_4\\ z_1-z_4 & z_2-z_4 & z_3-z_4 & z_4\\ 0 & 0 & 0 & 1 \end{vmatrix}= \begin{vmatrix} x_1 & x_2 & x_3 & x_4\\ y_1 & y_2 & y_3 & y_4\\ z_1 & z_2 & z_3 & z_4\\ 1 & 1 & 1 & 1\\ \end{vmatrix}=0 \]