题目链接:构造矩阵
题目描述
我们希望构造一个 n×m 的整数矩阵。
构造出的矩阵需满足:
每一行上的所有元素之积均等于 k。
每一列上的所有元素之积均等于 k。
保证 k 为 1 或 −1。
请你计算,一共可以构成出多少种不同的满足条件的矩阵。
由于结果可能很大,你只需要输出对 109+7 取模后的结果。
输入格式
共一行,包含三个整数 n,m,k。
输出格式
一个整数,表示对 109+7 取模后的结果。
数据范围
前 3 个测试点满足 1≤n,m≤3。
所有测试点满足 1≤n,m≤1018,k 为 1 或 −1。
难度:困难
时/空限制:1s / 256MB
总通过数:300
总尝试数:1360
来源:AcWing,第127场周赛
算法标签
样例
输入样例1:
1 1 -1
输出样例1:
1
输入样例2:
1 3 1
输出样例2:
1
输入样例3:
3 3 -1
输出样例3:
16
算法1
(两次快速幂) \(O(log(n-1*m-1))\)
套路:
把最下面一行和最右边一列拿出来,只考虑左上角这个n-1*m-1的小矩形的取法,这个小矩形每个方格可以取1或者-1,
一共2^(n-1)(m-1)种不同的取法,而对于每一行,只要确定了前m-1个,最后一个就确定了,对于每一列,只要确定了前n-1列,最后一个也确定了。
但是要注意,最右下角这个点,可能会无法确定
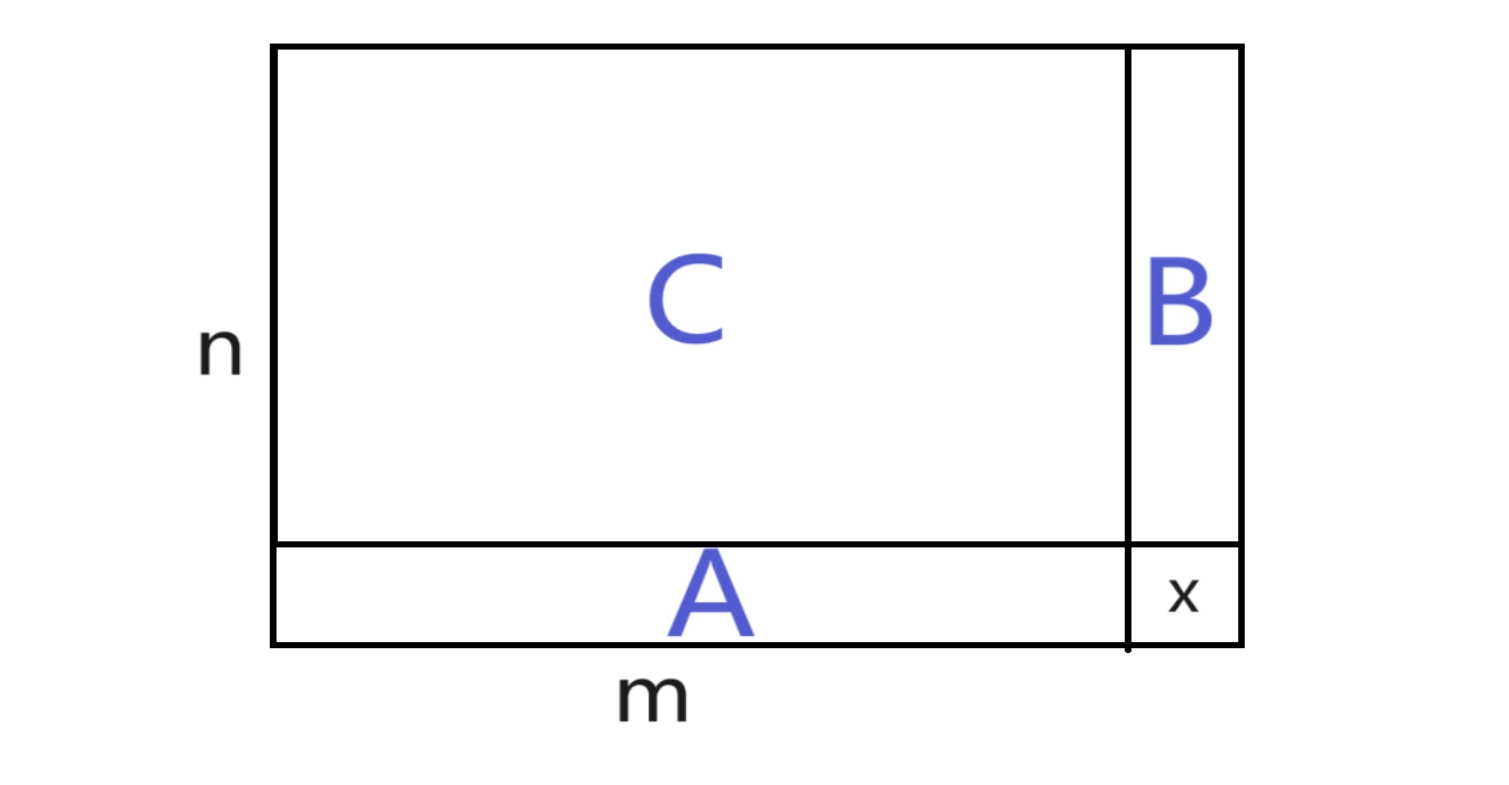
A B C 表示的是那个区域的乘积
看最后一行,由于每一行的乘积都是k,所以xA=k,所以x=k/A
看最右边一列,由于每一列的乘积都是k,所以xB=k,所以x=k/B
那么x如果想要确定,就必须得是 k/A=k/B,也就是A要等于B
而A,B都是有左上角的矩形确定的,
AC 是m-1列的乘积,每一列成绩是k,那么AC=k^(m-1)
BC 是n-1行的乘积,每一行成绩是k,那么BC=k^(n-1)
所以,A=k^(m-1) /C, B=k^(n-1)/C
想要让A=B,对于k=1,一定成立,对于k=-1,需要m-1和n-1奇偶性相同,否则不成立
而成立的情况,答案就是左上角的小矩形的填法,也就是2^(n-1)(m-1)种不同的取法,由于指数很大,所以可以做两次快速幂,或者用欧拉函数:因为我们知道 a^(p-1) 同余1modp,a与p互质,p为质数,所以我们可以把指数mod (p-1)
C++ 代码
#include<iostream>
using namespace std;
const int mod=10e9+7;
typedef long long LL;
LL qmi(LL a,LL k,LL p)
{
long long res=1;
while(k)
{
if(k&1)
{
res=res*a%p;
}
k>>=1;
a=a*a%p;
}
return res;
}
int main()
{
long long n,m,k;
cin>>n>>m>>k;
if(n==1||m==1)
{
cout<<1<<endl;
return 0;
}
LL p = qmi(2, n - 1, mod);
if((n + m) & 1) cout << 0;
else cout << qmi(p, m - 1, mod);
return 0;
}
算法2
(欧拉函数) \(O(log(n-1*m-1))\)
C++ 代码
#include<iostream>
using namespace std;
const int mod=1e9+7;
typedef long long LL;
LL qmi(LL a,LL k,LL p)
{
long long res=1;
while(k)
{
if(k&1)
{
res=res*a%p;
}
k>>=1;
a=a*a%p;
}
return res;
}
int main()
{
LL n, m, k;
cin >> n >> m >> k;
if (k == -1 && n % 2 != m % 2) puts("0");
else
{
LL t = (n - 1) % (mod - 1) * ((m - 1) % (mod - 1)) % (mod - 1);
cout << qmi(2, t, mod) << endl;
}
return 0;
}