Codeforces 编号在 1801-1825 之间的 Div.1,Div.2 only 和 EDU。
*1801. Codeforces Round 857 (Div. 1)
A. The Very Beautiful Blanket
尝试让每个 \(2\times 2\) 子矩形的异或和均为 \(0\)。
显然,若矩阵 \(A, B\) 满足条件,则矩阵 \(C_{i, j} = A_{i, j}\oplus B_{i, j}\) 也满足条件。
令 \(A_{i, j} = j\),\(B_{i, j} = i\)。为了最大化不同的数的数量,将 \(B_{i, j}\) 改成 \(2 ^ 8 i\) 即可。即 \(C_{i, j} = 2 ^ 8i + j\),显然 \(C_{i, j}\) 互不相同。
时间复杂度 \(\mathcal{O}(nm)\)。代码。
B. Buying gifts
枚举取到 \(m_2\) 的 \(b_i\),那么 \(m_1\) 不小于 \(\max_{b_j > m_2} a_i\)。
除此以外,\(b_j \leq m_2\) 且 \(i\neq j\) 的 \(a_j\) 可以任选,用 set 维护,查 \(m_2\) 在这样的 \(a_j\) 中的前驱后继。
按 \(b\) 从大到小排序后扫一遍。时间复杂度 \(\mathcal{O}(n\log n)\)。代码。
C. Music Festival
注意到重复播放一个专辑不会改变答案,且一个专辑只有严格前缀最大值有用。
设 \(f_i\) 表示以权值 \(i\) 结尾的答案。考虑专辑 \(b_1 < b_2 < \cdots < b_k\),那么 \(b_i\) 转移 \(f_{b_k}\gets \max_{p = 0} ^ {b_i - 1} f_p + (k - i + 1)\)。
前缀和优化,总转移数为 \(K = \sum k_i\),按 \(b_k\) 从小到大考虑所有转移即可。
离散化,时间复杂度 \(\mathcal{O}(K\log K)\)。代码。
D. The way home
关键性质:在城市 \(i\) 表演之后,不会在 \(w_j \leq w_i\) 的城市 \(j\) 表演。
设 \(f_i\) 表示到达城市 \(i\) 最少需表演多少次,\(g_i\) 表示对应剩余钱数。以 \(f\) 为第一关键字从小到大,\(g\) 为第二关键字从大到小,按 \(w_i\) 从小到大的顺序转移即可。
说明:对于两组贡献 \((f, g)\) 和 \((f', g')\),不妨设 \(f < f'\),若 \(g' > g + (f' - f) w_i\),说明对于 \((f', g')\) 对应的方案,一定可以少表演几次使得 \(f'\) 变成 \(f\),但 \(g'\) 仍大于 \(g\):在 \(i\) 之前表演的城市的 \(w\) 值小于 \(w_i\)。
跑 \(n\) 遍 Dijkstra 求出任意两点之间的最短路。时间复杂度 \(\mathcal{O}(nm\log m)\)。代码。
E. Gasoline prices
假设树是一条链,考虑求出第一个位置,使得两条路径该位置的点的代表元不同。BIT 维护哈希套二分,修改就启发式合并,在 BIT 上对应更新。
搬到树上就套个树剖即可。注意二分前将每段重链的哈希值先算好,保证单次检查只要查一段区间的哈希值。注意还要维护逆序哈希。
时间复杂度 \(\mathcal{O}((n + q)\log ^ 2n)\)。代码。
F. Another n-dimensional chocolate bar
将答案除掉 \(k\),设 \(f_i\) 表示切成 \(i\) 块的最大答案,发现 \(\lceil\frac k i\rceil\) 相同的 \(i\) 等价。
设 \(f_i\) 表示至少还要将数量乘以 \(i\) 的最大答案,初始值 \(f_k = 1\),转移枚举每个 \(d = \lceil\frac k i\rceil\),再枚举使得 \(\lceil \frac d j\rceil\) 相同的 \([l, r]\),用 \(f_d\lfloor\frac {a_i} l\rfloor\frac 1 {a_i}\) 更新 \(f_{\lceil\frac d l\rceil}\)。答案即 \(f_1k\)。
因为 \(\left\lceil\frac {\lceil \frac x a\rceil} b\right\rceil = \lceil\frac x {ab}\rceil\),所以算法正确。
时间复杂度类似杜教筛分析,为 \(\mathcal{O}(nk ^ {\frac 3 4})\)。代码。
*G. A task for substrings
设 \(f_i\) 表示 \(T[1, i]\) 的后缀有多少个是单词,\(g_i\) 表示最长的为 \(T[1, i]\) 的后缀的单词编号,\(h_i\) 表示 \(f\) 的前缀和。
对于每组询问,直接用 \(h_r - h_{l - 1}\) 回答询问,相当于求出了右端点在 \([l, r]\) 的子串单词数量,但没有保证左端点在 \([l, r]\) 范围内。
考虑找到最大的 \(q\) 使得 \(q - |s_{g_q}| + 1 \leq l\),那么以 \(q + 1\sim r\) 为右端点的合法子串单词数量就等于 \(h_r - h_l\),以 \(l\sim q\) 为右端点的合法子串数量就等于 \(s_{g_q}\) 的长度为 \(q - l + 1\) 的后缀有多少个子串是单词。
设 \(c_{i, j}\) 表示编号为 \(i\) 的单词的长度为 \(j\) 的后缀有多少个子串是单词,总状态数 \(S\),建反串 ACAM 预处理。
\(f, g, h\) 建正串 ACAM 预处理,线段树二分求 \(q\)。
时间复杂度 \(\mathcal{O}(S + |t| + m\log |t|)\)。不难看出算法是 在线 的。代码。
*1804. Nebius Welcome Round (Div. 1 + Div. 2)
A. Lame King
令 \(a\gets |a|\),\(b\gets |b|\) 不改变答案。
当 \(a = b\) 时,答案显然为 \(a + b\)。
否则不妨设 \(a > b\),那么最优策略是:向上向右交替走到 \((b + 1, b)\),然后停一次,向上走一步。答案为 \(a + b + |a - b| - 1\)。
B. Vaccination
考虑若干人可以打一包疫苗的充要条件:来得最早的人和来得最迟的人的时刻相差不超过 \(d + w\),且总人数不超过 \(k\)。直接按时间顺序贪心即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
C. Pull Your Luck
注意到 \(\binom {i} 2 \equiv \binom {i\bmod 2n} 2\pmod n\),所以令 \(p\gets \min(p, 2n)\) 即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
D. Accommodation
每一行独立,对每一行分别做。
设开灯总数为 \(c\),两个灯都开的双人房数量为 \(x\),那么被占用的房间数为 \(c - x\)。
最小化被占用的房间总数,等价于最大化 \(x\)。直接贪,扫一遍,能放就放。证明一定合法:不超过 \(\frac m 4\) 个双人间将序列割成了不超过 \(\frac m 2\) 段,每段都可以用至多一个单人间调整奇偶性。
最大化被占用的房间总数,等价于最小化 \(x\)。类似地,扫一遍,能放(至少一个灯没开)就放。
时间复杂度 \(\mathcal{O}(nm)\)。代码。
E. Routing
连边 \(u\to a(u)\),得到基环森林。每棵基环树的环上所有点的邻居必须为全集,否则从环上的点出发,存在无法到达的点。
考虑一个邻居为全集的环,从环上每个点出发 DFS 剩下的点,记录每个点的父亲,得到一组合法方案。
问题转化为找到邻居为全集的环。枚举起点,设 \(f_S\) 表示从起点出发经过 \(S\) 最终能到达哪些点,转移即枚举 \(k\in N(f_S)\backslash S\),找到后也容易构造方案。
时间复杂度 \(\mathcal{O}(2 ^ nn ^ 2)\)。代码。
钦定起点为编号最小的点即可做到 \(\mathcal{O}(2 ^ nn)\)。代码。
*F. Approximate Diameter
很优雅的暴力。
首先,因为 \(d(i, j)\leq d(1, i) + d(i, j)\),所以 \(2\max d(1, i) \geq d(G)\)。至此可以做到 \(\mathcal{O}(q(n + m + q))\)。
上述做法没有用到答案可以在 \((d(G), 2d(G)]\),想要用也很简单,假设 \(d(G_i)\) 求出的答案为 \(f_i\),那么对于 \(\frac {f_i} 2\leq f_j\leq f_i\) 的 \(G_j\),输出 \(f_i\) 也合法。又因为 \(d(G)\) 单调不增,所以每次二分出最后一个使得 \(2f_j\geq f_i\) 的 \(j\),将 \(f_{i\sim j}\) 均赋为 \(f_i\)。
因为每次二分答案至少减半,所以总复杂度 \(\mathcal{O}((n + m + q)\log ^ 2q)\)。代码。
直接分治复杂度是一样的,边界条件 \(2f_r\geq f_l\)。代码。
*G. Flow Control
除以 \(2\) 下取整,很难让人不想到自然 \(\log\)。
先假设没有插入和删除,那么每次被挤爆会导致序列极差变成原来的一半,在 \(\log\) 次挤爆之后就变成了会循环的平凡情况:所有数全部相同,或者除以 \(2\) 下取整之前分别是 \(2k - 1\) 和 \(2k\)。
考虑用 set 维护值域连续段,剩下来就是暴力模拟了。
一个细节:删除时需要知道删除的数的值,对 set 每个元素额外维护对应下标,每次修改时更新下标对应的值,注意涉及到合并要用并查集。或者直接把 set 改成线段树,区间不全相同就递归下去修改,势能分析得到同样的复杂度。
时间复杂度 \(\mathcal{O}(n\log ^ 2 b)\)。细节有点多。代码。
*H. Code Lock
很厉害的题目。
设 \(w(x, y)\) 表示 \(x, y\) 在密码串中相邻出现了多少次,那么问题相当于求排列 \(p\) 最小化
如果按顺序 DP,要记录 \(p\) 的顺序,那就彻底寄了:无论如何都无法避免 \(15 ^ {\underline {7}}\)。只能换一种 DP 方式了。
设 \(L = \lceil \frac n 2\rceil\),将贡献拆到每个点上,分成 \(i < L\) 和 \(L\leq i < n\) 讨论。钦定当 \(j - i < L\) 时 \(\min\) 取 \(j - i\),否则 \(\min\) 取 \(n - j + i\)。
对于 \(i < L\),有
对于 \(i\geq L\),有
首先枚举 \(S = \{p_{0\sim L - 1}\}\)。
对于 \(i < L\),需要知道 \(\{p_{0\sim i - 1}\}\) 和 \(\{p_{i + 1\sim L - 1}\}\) 中的任意一个,以及 \(\{p_{L\sim i + L - 1}\}\) 和 \(\{p_{i + L\sim n - 1}\}\) 中的任意一个。
对于 \(i \geq L\),需要知道 \(\{p_{0\sim i - L}\}\) 和 \(\{p_{i - L + 1\sim L - 1}\}\) 中的任意一个,以及 \(\{p_{L\sim i - 1}\}\) 和 \(\{p_{i + 1\sim n - 1}\}\) 中的任意一个。
发现如果按照 \(p_0, p_L, p_1, p_{L + 1}, \cdots\) 的顺序加入元素,只要维护已经加入的元素集合 \(T\),就可以计算 \(c(i)\)。状态数为 \(\sum_{x = 0} ^ L \sum_{y = x - 1} ^ {x} \binom {L} {x} \binom {n - L} {y}\)。还要乘以枚举 \(S\) 的 \(\binom n L\)。
状态数有点多,不妨钦定 \(p_0 = 0\),这样是 \(\binom {n - 1} {L - 1} \sum_{x = 1} ^ L \sum_{y = x - 1} ^ {y} \binom {L - 1} {x - 1} \binom {n - L} {y}\approx 8.3\times 10 ^ 7\),再乘以枚举下一个位置的复杂度,可以接受。
代码。
*1805. Codeforces Round 862 (Div. 2)
A. We Need the Zero
对于 \(2\mid n\),要求 \(a_i\) 异或和为 \(0\),输出任意数。
对于 \(2\nmid n\),输出 \(a_i\) 异或和。
B. The String Has a Target
对于 a 到 z 的每个字符,一定是将最后一次出现移到最前面,模拟即可。
时间复杂度 \(\mathcal{O}(n\Sigma)\)。代码。
只要将最小的字符的最后一次出现移到最前面就行了!我是憨憨。
C. Place for a Selfie
考虑无交点的充要条件:\(ax ^ 2 + bx + c = kx\) 无解,即 \(\Delta = (b - k) ^ 2 - 4ac < 0\),即 \(b - \sqrt {4ac} < k < b + \sqrt {4ac}\)。
用 set 维护斜率查前驱后继即可。注意边界处的处理。
时间复杂度 \(\mathcal{O}(m\log n)\)。代码。
D. A Wide, Wide Graph
如果一个点和其它点有连边,那它一定和直径的某一端有连边。
求出每个点到直径两端的距离最大值 \(f_i\)。对于 \(k > f_i\),这个点一定是孤立点。对于 \(k \leq f_i\),这个点一定和直径一端相连,而直径两端相连,所以所有 \(f_i\geq k\) 的 \(i\) 形成一个连通块。
因此,对于 \(k\leq \mathrm{diam}\),答案为 \(f_i < k\) 的 \(i\) 的数量加 \(1\)。对于 \(k > \mathrm{diam}\),答案显然为 \(n\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
E. There Should Be a Lot of Maximums
dsu on tree 并用两个 set 分别维护子树内和子树外所有 \(\mathrm{occ} \geq 2\) 的数。可以做任意 \(\mathrm{occ} \geq k\)。
时间复杂度 \(\mathcal{O}(n\log ^ 2n)\)。代码。
另解:对于 \(\mathrm{occ} \geq 3\) 的数,一定产生贡献。对于 \(\mathrm{occ} = 1\) 的数,一定不产生贡献。对于 \(\mathrm{occ} = 2\) 的数,只有一条链不产生贡献。找到最大的 \(\mathrm{occ} = 2\) 的数,这条链以外的边的答案好算,对于这条链只需以两端分别为根 DFS 即可。时间复杂度可做到除离散化外 \(\mathcal{O}(n)\)。
另解:DFS 序拍平并复制一份,相当于区间查询 \(\mathrm{occ} \geq 2\) 的最大值。将所有询问离线下来后扫描线,用权值线段树维护每个数倒数第 \(2\) 次出现的位置,查询在线段树上二分。可以做任意 \(\mathrm{occ} \geq k\)。时间复杂度 \(\mathcal{O}(n\log n)\)。
*F2. Survival of the Weakest (hard version)
好题。
首先钦定 \(a\) 不降,考虑 F1 的 \(n\leq 3000\) 怎么做。
值域太大肯定不能直接模拟,那就想办法减小值域,可以想到维护值 \(s\) 和序列 \(b\) 表示 \(a_i = b_i + s\),其中 \(s\) 为 \(\min a_i\)。比较 \(a_i + a_j\) 和 \(a_{i'} + a_{j'}\) 时,只要比较 \(b_i + b_j\) 和 \(b_{i'} + b_{j'}\)。注意到一次操作后新的 \(a'_{n - 1}\) 和 \(a'_{1}\) 相差不超过 \(a_n - a_2 \leq a_n - a_1\)(\(a_1 + a_{2\sim n}\) 可以贡献前 \(n - 1\) 小值),所以新的 \(b'_{n - 1}\) 不大于原来的 \(b_n\)。值域不会增大,可行。
每次将 \(s\) 变为 \(a_1 + a_2\) 即 \(2s + b_2\)(\(b_1 = 0\)),然后模拟即可。模拟就是经典超级钢琴,根据 \(b\) 的单调性直接双指针 + 优先队列维护,不用可持久化线段树。
歪解:
首先有个猜测是 \(b\) 会在很短的时间内缩减为 \(0\),这是错的:\([0, 1, 2, 10 ^ 9, 10 ^ 9, 10 ^ 9, \cdots]\),每次将 \(b_{4\sim n}\) 减去 \(b_2 = 1\),\(b_2\) 变成 \(b_3 - b_2\)。这组数据启发我们得到算法:如果 \(b_4 - b_2\geq b_3\),那么将 \(b_{4\sim n}\) 全部减去 \(b_2\),\(b_2\) 变成 \(b_3 - b_2\)。全部减去的过程直接打标记即可。这也是错的:代码。
为什么会错呢?仔细思考,我们发现将 \(b_{4\sim n}\) 全部减去 \(b_2\) 只有在 \(b_2 + b_4 \geq b_1 + b_n\) 的时候合理,所以判断当 \(b_n - b_4\leq b_2\) 的时候再执行该操作。然而还是 TLE。打个表(\(a_{1\sim 3}\) 很小,\(a_{4\sim n}\) 很大)发现 \(b_n - b_4\) 的收敛速度不尽如人意:考虑 \([0, 1, 2, 10 ^ 9 - 2, 10 ^ 9, 10 ^ 9, \cdots]\),每次操作会 \(b_{4\sim n}\) 减去 \(1\),然后将 \(b_i\)(\(i\) 等于操作编号加 \(4\))再减去 \(1\)(来自 \(b_3\) 和 \(b_4\) 的贡献),这要收敛到猴年马月去了。
我们充分发挥人类智慧:猜测编号较大的位置没有用,将判断条件改成 \(b_{X} - b_4\leq b_2\),其中 \(X\) 是一个比较小的数。这样就可以 通过 了,但不知道为啥对。
疑点:将 \(b_2\) 改成 \(b_3\) 还是可以 通过,但不知道为啥对。
知道上述两个做法为啥对或者有 hack 数据可以教育一下(如何保证正确性和复杂度)。
感觉告诉我们较大的元素是没有用的:它们会在之后的操作被 “弹出”。弹出即新的序列没有和该元素有关的和。如果 \(b_n\) 没有被弹出,那么 \(b_2 + b_3 \geq b_n\)。操作后得到序列 \([0, b_3 - b_2, \cdots, b_n - b_2]\)。发现再操作一次,序列末尾的数不大于 \((b_n - b_2) - (b_3 - b_2) = b_n - b_3\)。
注意到 \(b_2 + b_3 \geq b_n\),即 \(2b_3\geq b_n\)。这说明如果存在一次操作没有弹出 \(b_n\),那么 \(b_n\) 在第二次操作之后至少减半。
发现上述结论对任何 \(b_i\) 都成立:若 \(b_2 + b_3 \geq b_i\),那么 \(b_i\) 在第二次操作之后至少减半。这给予我们只保留前 \(L = 2\log a_i + \epsilon\) 个元素的想法。
证明:对于一次操作:
- 若 \(b_2 + b_3\leq b_L\),那么由 \(b_{1\sim L}\) 可以确定新的正确的 \(b'_{1\sim L}\)。
- 若 \(b_2 + b_3 > b_L\),那么至少新的 \(b'_{1\sim L - 1}\) 是对的。再操作一次,至少新的 \(b''_{1\sim L - 2}\) 是对的,且 \(2b''_{L - 2}\leq b_L\)。不妨令 \(L\) 减去 \(2\)。
因为情况二最多发生 \(\log a_i\) 次(当 \(b_L\) 变成 \(0\) 时,\(b_2 = b_3 = 0\),不可能发生情况二),使得 \(L\) 减去 \(2\log a_i\),而 \(L > 2\log a_i\),所以一定能求出正确的 \(b_1\),算法正确。
因此,只保留序列 \(a\) 的前 \(L\) 个元素,每次仅根据 \(a_{1\sim L}\) 求出新的 \(a'_{1\sim L}\)(注意这不改变序列长度),模拟操作 \(n - 1\) 次,则 \(a_1\) 即为所求。
需要特判 \(n = 2\)。
时间复杂度 \(\mathcal{O}(n\log V\log\log V)\)。代码。
*1806. Codeforces Round 858 (Div. 2)
A. Walking Master
每次向右上或向下走 \(1\) 单位,于是对坐标轴进行剪切变换,即令 \((x, y)\to (y - x, y)\),那么每次令第一维或第二维加 \(1\)。
检查是否有 \(b - a\leq d - c\) 且 \(b\leq d\) 即可,答案即 \((d - c) - (b - a) + d - b\)。
B. Mex Master
如果 \(2c_0 - 1\leq n\),那么可以在所有奇数位置上放 \(0\),分数为 \(0\)。
否则若序列只有 \(01\),那么分数为 \(2\)。
否则可以用非 \(1\) 正整数隔开 \(0\) 和 \(1\),分数为 \(1\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
C. Sequence Master
假设所有数相同,有 \(n = 1\) 或 \(q = 0\) 或 \((n, q) = (2, 2)\) 的平凡解。
接下来不妨设 \(q_1 \neq q_2\),令 \(S' = [3, n + 1]\),根据 \(S\cup \{1\}\) 和 \(S\cup \{2\}\) 的条件可得方程 \((q_1 - q_2)(q_3 q_4\cdots q_{n + 1} + 1) = 0\),那么 \(\prod_{i\in S} q_i = -1\)。
又因为所有 \(S'\subseteq [3, 2n]\) 且 \(|S'| = n - 1\),均有 \(\prod_{i\in S} q_i = -1\),得 \(q_{3\sim 2n}\) 相等。
所以当 \(n\) 为偶数时,没有其它解。当 \(n\) 为奇数时,\(q_{3\sim 2n} = -1\)。接下来容易推出 \(q_1 = n\),\(q_2 = -1\),因此序列中恰有一个 \(n\),其它元素为 \(-1\),贡献为 \((\sum_{i = 1} ^ {2n} |a_i + 1|) + \min_{i = 1} ^ {2n} (|a_i - n| - |a_i + 1|)\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
*D. DSU Master
好题。
考虑一个 \(p_i\) 产生贡献的充要条件:\(p_{1\sim i - 1}\) 中出现了 \(1\sim p_i - 1\) 所有元素,且此时 \(1\) 没有出边。
设 \(f_i\) 表示 \(k = i\) 的答案,考虑递推:将值 \(i + 1\) 插入所有 \(i\) 阶排列。
性质:只要不将 \(i + 1\) 插到最后,那么它一定不产生贡献。显然。
性质:将 \(i + 1\) 插到任何位置不对已经产生的贡献产生影响。证明:因为 \(i + 1\) 对应的操作一定不会涉及到包含 \(1\) 的连通块,所以不会打破其它产生贡献的元素的产生贡献的条件。
如果将 \(i + 1\) 插到最后,那么它产生贡献当且仅当前 \(i\) 次操作后 \(1\) 没有出边。因此,设 \(g_i\) 表示 \(k = i\) 时操作后 \(1\) 没有出边的排列,则 \(g_0 = 1\),且 \(g_i = g_{i - 1} (i - a_i)\),\(f_0 = 0\) 且 \(f_i = f_{i - 1} i + (1 - a_i) g_{i - 1}\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
*E. Tree Master
这题也挺不错,考察了对根号分治的理解。
记忆化后直接暴力就是对的:设 \(s_i\) 表示深度为 \(i\) 的结点数量,对于所有 \(s_i\leq \sqrt n\),总共只有 \(\sum s_i ^ 2\leq n\sqrt n\) 对点。对于每层 \(s_i > \sqrt n\),每个询问只会涉及到一对点,因为这样的层数不超过 \(\sqrt n\),所以总共只有不超过 \(q\sqrt n\) 对点。
使用 map 或 unordered_map 会 TLE,手写哈希表即可通过。
时间复杂度 \(\mathcal{O}(n\sqrt n)\)。代码。
*F2. GCD Master (hard version)
很好的猜性质题目。
对最终序列的每个元素 \(b_i\),用集合 \(S_i\) 描述它是由原序列哪些元素求 \(\gcd\) 得到的。考虑两个大小不小于 \(2\) 的 \(|S_i|, |S_j|\),不妨设 \(b_i \leq b_j\)。我们将 \(S_j\) 中最大的元素 \(c_j\) 单独拎出来,其它元素并到 \(|S_i|\) 里面去,发现这样做产生 \(\Delta = c_j - b_i - b_j + \gcd(b_i, b_j)\)。注意 \(b_i\leq b_j\) 且 \(b_j\mid c_j\),如果 \(b_j\neq c_j\),那么 \(\Delta > 0\)。那么不妨设 \(a_i\) 互不相同,就满足条件了。得到结论:若 \(a\) 互不相同,那么恰好存在一个 \(|S_i| > 1\),其它 \(|S_i| = 1\)。
\(a\) 存在相同的元素怎么办呢?注意到将相同的元素合并一定不劣,所以如果去重之后的 \(a\) 消耗了 \(k'\) 步操作,那么还要操作 \(k - k'\) 次。将多余元素从小到大排序取前 \(k - k'\) 个求和,从总和中减去即可。问题转化为对去重后的 \(a\) 求每个 \(k'\leq k\) 的答案。
枚举 \(|S_i| > 1\) 的 \(b_i\),然后从小到大枚举它的所有倍数 \(tb_i\),属于 \(S_i\) 的一定是一段前缀。设当前考虑了 \(k'\) 个元素,总和为 \(s'\),若 \(k' > 1\),那么还需要 \(k - (k' - 1)\) 次删去相同元素的操作。时间复杂度 \(\mathcal{O}(n\log n + m\log m)\),\(\log n\) 因子可以去掉,可通过 F1。代码。
观察:操作 \((i, j)\) 之后,总和至少减去 \(\max(a_i, a_j)\),自然想到不要操作特别大的数。将 \(a\) 排序后,不妨先取 \(a_{1\sim k + 1}\),然后调整。
设原 \(\gcd\) 为 \(d\),那么代价为 \(-d + \sum_{i = 1} ^ {k + 1} a_i\)。调整的核心在于,将 \(\sum a\) 变大一些,然后让 \(d\) 变得大很多。注意到 \(d\) 不大于任何两个相邻元素的差,所以调整超过一个元素是不优的:假设 \(a_i, a_j\) 被选中,其中 \(k + 1 < i < j\),那么 \(\sum a\) 至少大了 \(a_j - a_i\),但新的 \(d'\leq a_j - a_i\),不优。
进一步地,可以证明调整 \(a_i\) 一定不优,其中 \(i\leq k\):设 \(a_i\) 调整为 \(a_j\),其中 \(k + 1 < j\),发现 \(\sum a\) 增加 \(a_j - a_i\geq a_j - a_{k - 1}\),但新的 \(d'\leq a_j - a_{k - 1}\),不优。
因此,设 \(d_k = \gcd_{i = 1} ^ k a_i\),问题转化为求 \(\max_{i = k + 1} ^ n \gcd(d_k, a_i) - a_i\)。
又因为 \(d_k\mid d_{k - 1}\),所以随着 \(k\) 增大,\(d_k\) 只会改变 \(\mathcal{O}(\log a)\) 次,每次增大后重新求 \(\gcd(d_k, a_i) - a_i\) 的后缀最大值即可。总时间复杂度 \(\mathcal{O}(n\log ^ 2m)\)。
很显然,\(\gcd(d_k, a_i)\) 的计算可以均摊。记录 \(o_i = \gcd(d_k, a_i)\),每次 \(d_k\) 改变时令 \(o_i \gets \gcd(d_k, o_i)\),势能分析过程的总复杂度是 \(\mathcal{O}(n\log m)\)。
总时间复杂度 \(\mathcal{O}(n(\log n + \log m))\)。注意使用 __int128,代码。
*1808. Codeforces Round 861 (Div. 2)
A. Lucky Numbers
从 \(l\) 到 \(r\) 枚举,如果找到幸运值为 \(9\) 的直接输出。
因为枚举 \(100\) 个数之后一定存在以 \(90\) 结尾的数,所以每次不会枚举超过 \(100\) 个数。
B. Playing in a Casino
考虑所有卡片上第 \(i\) 个数的贡献。设它们形成长为 \(n\) 的序列 \(c\),将 \(c\) 从小到大排序,那么 \(c_i\) 和 \(c_{j < i}\) 产生总和为 \((i - 1) c_i\) 的贡献,和 \(c_{j > i}\) 产生总和为 \(-(n - i) c_i\) 的贡献。
时间复杂度 \(\mathcal{O}(nm\log n)\)。代码。
C. Unlucky Numbers
数位 DP,设 \(f_{i, a, b, x, y}\) 表示还剩 \(0\sim i - 1\) 位没有考虑,已经填的数码最小值为 \(a\),最大值为 \(b\),是否顶到 \(l\) 的下界和是否顶到 \(r\) 的上界时,已经填的数码形成的数或无解。转移即枚举下一位数码 \(d\),先判是否合法,若合法则求出新的 \(a', b', x', y'\),将 \(f_{i - 1, a', b', x', y'}\) 赋值为 \(10f_{i, a, b, x, y} + d\)。注意判还没有填任何数码的情况。
时间复杂度 \(\mathcal{O}(\log_k V k ^ 3)\),其中 \(k\) 表示进制数。代码。
一个值得借鉴的思路:将 \([l, r]\) 拆成若干 \([x, x + 10 ^ a)\),满足 \(10 ^ a\mid x\)。每个区间的答案显然为 \(f(\frac x {10 ^ a})\)。
D. Petya, Petya, Petr, and Palindromes
不妨先认为答案是 \((n - k + 1) \frac {k - 1} 2\),再减去可以减小答案的下标二元组 \((i, j)\) 的数量,满足:
- \(i < j\)。
- \(a_i = a_j\)。
- \(j - i < k\)。
- \(i + j > k\)。
- \(i + j \leq 2n - k + 1\)。
- \(i\equiv j\pmod 2\)。
其中第四个和第五个限制容易漏:有些位置是无法成为回文中心。
对于所有值相同的下标序列 \(b\),枚举 \(i\),用三个指针分别维护第三、四、五个条件对应的 \(j\) 的边界。注意根据 \(i\) 的方向确定指针的初始位置和方向。
第三、五个条件限制了 \(j\) 的最大值,第一、四个条件限制了 \(j\) 的最小值。求出边界后,查询 \(b\) 的一段区间上有多少个奇数,或查询有多少个偶数,前缀和维护。
时间复杂度 \(\mathcal{O}(n + a)\)。代码。
E3. Minibuses on Venus (hard version)
一
设 \(s = (\sum a_i) \bmod k\),不存在 \(2a_i\equiv s\pmod k\)。
补集转化,枚举 \(s\),设 \(f_{i, j}\) 表示长度为 \(i\) 且总和为 \(j\) 的非法序列,转移即枚举 \(2a_{i + 1}\not\equiv s\pmod k\),\(f_{i, j}\to f_{i + 1, (j + a_i)\bmod k}\)。
对每个 \(s\) 的 \(f_{n, s}\) 求和,再用 \(k ^ n\) 减掉,即为答案。
时间复杂度 \(\mathcal{O}(n k ^ 3)\),可以通过 E1。代码。
二
先把 \(k = 1\) 判掉。
当 \(2\nmid k\) 时,对每个 \(s\in [0, k - 1]\),存在恰好一个 \(x\) 使得 \(2x\equiv s\pmod k\),即 \(x = \begin{cases} \frac s 2 & (2\mid s) \\ \frac {s + k} 2 & (2\nmid s) \end{cases}\)。将 \(a_i\) 减去 \(x\),问题转化为:求 \(\sum a_i\equiv s - nx\pmod k\) 且包含 \(0\) 的序列数量。补集转化,套用 E1 的 DP,可知对于 \(1\leq j < k\),\(f_{i, k}\) 相等。有递推式 \(f_{i, 0} = (k - 1) f_{i - 1, 1}\),\(f_{i, 1} = f_{i - 1, 0} + (k - 2) f_{i - 1, 1}\)。矩阵快速幂求出 \(f_{n, 0 / 1}\),再根据 \(s - nx\) 是否为 \(k\) 的倍数计算答案。
当 \(2\mid k\) 时,对每个 \(s\in [0, k - 1]\),若 \(2\nmid s\),则所有序列均不合法,否则恰存在两个 \(x\) 使得 \(2x \equiv s\pmod k\),记为 \(x_1\) 和 \(x_2\),则 \(x_1 = \frac s 2\),\(x_2 = \frac {s + k} 2 = x_1 + \frac k 2\)。将 \(a_i\) 减去 \(x_1\),问题转化为:求 \(\sum a_i\equiv s - nx_1\) 且包含 \(0\) 或 \(\frac k 2\) 的序列数量。补集转化,套用 E1 的 DP,可知对于 \(i\geq 1\),\(f_{i, 0} = f_{i, \frac k 2}\),且对于所有 \(j\in [1, \frac k 2 - 1]\cup [\frac k 2 + 1, k - 1]\),\(f_{i, j}\) 相等。有递推式 \(f_{i, 0} = (k - 2) f_{i - 1, 1}\),\(f_{i, 1} = 2f_{i - 1, 0} + (k - 4)f_{i - 1, 1}\)。注意该递推式对于 \(i = 1\) 不成立。同样可以矩阵快速幂解决。
时间复杂度 \(\mathcal{O}(k + \log n)\)。代码。
三
对于 \(2\nmid k\),瓶颈在于计算 \(s - nx\equiv 0\pmod k\) 的 \(s\) 的数量。因为 \(s = 2x\) 且 \(s\) 和 \(x\) 一一对应,所以相当于计算 \((n - 2)x\equiv 0\pmod k\) 的 \(x\) 的数量。典中典,\(x\) 必须是 \(\frac {k} {\gcd(n - 2, k)}\) 的倍数,在 \([0, k)\) 里面恰有 \(\gcd(n - 2, k)\) 个。
对于 \(2\mid k\),瓶颈在于计算 \(s - nx_1\equiv 0\pmod k\) 或 \(s - nx_1 \equiv \frac k 2\pmod k\) 的 \(s\) 的数量,即 \(n - sx_1\equiv 0\pmod {\frac k 2}\)。因为 \(s = 2x_1\) 且 \(s\) 和 \(x_1\) 一一对应,所以相当于计算 \((n - 2)x_1\equiv 0 \pmod {\frac k 2}\) 的 \(x\) 的数量。因为 \(0\leq x_1 < \frac k 2\),所以类似地,\(x_1\) 的数量为 \(\frac {k / 2} {\gcd(n - 2, k / 2)}\)。
时间复杂度 \(\mathcal{O}(\log k + \log n)\)。注意特判 \(n = 1\)。代码。
四
对于 \(2\nmid k\),打表观察发现对于偶数 \(i\) 有 \(f_{i, 1} = f_{i, 0} - 1\),对于奇数 \(i\) 有 \(f_{i, 0} = f_{i, 1} + 1\),即 \(f_{i, 1} = f_{i, 0} + (-1) ^ {i - 1}\),容易归纳证明。由此可知 \(f_{n, 0} = vf_{n - 1, 1} = v(f_{n - 1, 0} + (-1) ^ {n - 1})\),即 \(((((0 + 1) \cdot v - 1)\cdot v + 1) \cdot v - 1)\cdots v\),共乘以 \(n - 1\) 个 \(v\),其中 \(v = k - 1\)。将括号拆开,发现就是 \(\sum_{i = 1} ^ {n - 1} (-1) ^ {i - 1} v ^ {n - i}\),变形得 \((-1) ^ {n - 1} \sum_{i = 1} ^ {n - 1} (-1) ^ {n - i} v ^ {n - i}\),等比数列求和得 \((-1) ^ {n - 1} \frac {(-v) ^ n - (-v) ^ 1} {-v - 1}\),即 \((-1) ^ n \frac {(1 - k) ^ n - (1 - k)}{k}\)。设 \(c = \gcd(n - 2, k)\),推式子:
因此对于 \(2\nmid k\),答案为 \(k ^ n - (k - 1) ^ n + (-1) ^ n (\gcd(n - 2, k) - 1)\)。
对于 \(2\mid k\),打表观察发现有 \(f_{i, 1} = f_{i, 0} + (-2) ^ {i - 1}\)。一个感性理解:\(2\mid k\) 的 DP 相当于两个规模为 \(\frac k 2\) 的 \(2\nmid k\) 的 DP(注意不是分成两个子问题,只是借用 DP 转移方式),而两个 DP 之间是对称的,产生双倍贡献。类似地,得到递推式 \(f_{n, 0} = (k - 2) f_{n - 1, 0} = (k - 2)(f_{n - 1, 0} + (-2) ^ {n - 2})\)。对比它和 \(2\nmid k\) 的 DP 递推式 \(f_{n, 0} = (k - 1)(f_{n - 1, 0} + (-1) ^ {n - 1})\),结合之前的感性理解,即做规模为 \(\frac k 2\) 的 \(2\nmid k\) 的 DP 且每次系数翻倍,考虑设 \(g_{n, 0} = \frac {f_{n, 0}} {2 ^ {n - 1}}\),得 \(g_{n, 0} = (\frac k 2 - 1)(g_{n - 1, 0} + (-1) ^ {n - 1})\)。对于 \(g_{n, 1}\) 类似,有 \(f_{n, 1} = g_{n, 1}2 ^ {n - 1}\)。所以,先做规模为 \(\frac k 2\) 的 \(2\nmid k\) 的 DP 得到 \(g\),然后根据 \(g\) 反推出 \(f\):仅仅是将答案乘以 \(2 ^ {n - 1}\)。设 \(k' = \frac k 2\),\(c' = \gcd(n - 2, k')\):
因此对于 \(2\mid k\),答案为 \(\frac {k ^ n} 2 - 2 ^ {n - 1}((\frac k 2 - 1) ^ n + (-1) ^ n (\gcd(n - 2, \frac k 2) - 1))\)。
时间复杂度 \(\mathcal{O}(\log k + \log n)\),但是封闭形式。代码。
五
不觉得打表找规律有点不牛吗?
设 \(F_n\) 表示 \(n\) 个 \([1, k)\) 之间的数之和为 \(k\) 的倍数的方案数,则 \(F_n = f_{n, 0}\)。
考虑任意填 \(a_1\sim a_{n - 1}\),最后用 \(a_n\) 补成 \(k\) 的倍数。发现当且仅当 \(k\mid \sum a_{1\sim n - 1}\) 时不合法,得到递推式 \(F_n = (k - 1) ^ {n - 1} - F_{n - 1}\)。注意边界 \(F_1 = 0\),这直接说明 \(F_n = \sum_{i = 1} ^ {n - 1} (k - 1) ^ {n - i} (-1) ^ {i - 1}\)。
对于 \(f_{n, 1}\),推导是类似的。
六
除了上述做法外,还存在根据 “不能放 ……” 的限制二项式反演 + 推式子的做法。不过该做法比较平凡,就不赘述了。
*1809. Educational Codeforces Round 145
A. Garland
当 \(\max occ_c \leq 2\) 时,答案为 \(4\)。
当 \(\max occ_c = 3\) 时,答案为 \(6\)。
当 \(\max occ_c = 4\) 时,显然无解。
B. Points on Plane
二分答案,考虑 \(m\) 是否有解。
取遍所有 \(x + y\) 和 \(m\) 奇偶性相同的 \((x, y)\),形成若干边长为 \(\sqrt 2\) 的小正方形,总共可以选择 \((m + 1) ^ 2\) 个点。
因此,答案即最小的 \(x\) 使得 \((x + 1) ^ 2 \geq n\)。
C. Sum on Subarrays
设前缀和数组为 \(s\),初始令 \(s_i = -i\)。
每将一个 \(s_i\) 变为 \(i\),都会增加 \(i\) 个和为正数的子序列。从后往前贪心即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
D. Binary String Sorting
可以证明最多交换一次。
枚举 \(01\) 分界线,求出要删除几次,再检查是否可以用交换减小代价。
时间复杂度 \(\mathcal{O}(n)\)。代码。
E. Two Tanks
注意到 \(c + d\) 不变。枚举 \(c + d\),则用第一个水箱的水量即可描述状态。
考虑对所有 \(c\) 求答案。
对于两个初始状态 \(c, c'\),如果任意时刻它们的值相同,则它们的答案相同。导致值相同的原因就是两个水箱满了或空了。
显然,当 \(a\) 很小或 \(a\) 很大的时候,这种情况越容易发生。而如果这种情况没有发生,则最终的 \(c\) 就等于初始的 \(c\) 减去 \(\sum v_i\)。
因此,答案形如 \([x, x, x + 1, x + 2, \cdots, y - 2, y - 1, y, y]\),直接二分的时间复杂度为 \(\mathcal{O}(n(a + b)\log (a + b))\)。代码。
设 \(l\) 表示 \(\leq l\) 的答案相同,\(r\) 表示 \(\geq r\) 的答案相同,依次考虑每个操作并更新 \(l, r\),时间复杂度 \(\mathcal{O}(n(a + b))\)。
F. Traveling in Berland
因为油价只有 \(1\) 或 \(2\),所以遇到 \(1\),我们一定能加满就加满,实在没油才会加 \(2\)。
不妨钦定到每个 \(1\) 时油箱恰好为空。如果不为空,则当前油箱里的油的单价不小于 \(1\),替换为当前城市的油不劣。
考虑从城市 \(i\) 出发到另一个城市 \(j\) 的代价 \(f(i, j)\),满足中途没有 \(1\),且出发前和到达后油箱均为空。设距离为 \(d\)。当出发城市油价为 \(2\) 时,代价为 \(2d\)。当出发城市油价为 \(1\) 时,若 \(d\leq k\),代价为 \(d\),否则代价为 \(2d - k\)。
破环成链,考虑 \(i\to i + n\) 中途的所有油价为 \(1\) 的城市 \(p_1, p_2, \cdots, p_k\),则 \(f(i, p_1) + f(p_k, i + n) + \sum_{j = 1} ^ {k - 1} f(p_j, p_{j + 1})\) 即为所求。
倍增,设 \(f_{i, j}\) 表示从 \(j\) 出发跳 \(2 ^ i\) 步(每一步跳到下一个 \(1\))到达的城市及对应代价。时间复杂度 \(\mathcal{O}(n\log n)\)。代码。
因为出发城市和到达城市单调增,所以双指针维护可做到 \(\mathcal{O}(n)\)。
*G. Prediction
考虑符合要求的 \(a\) 的排列 \(b\),两个选手比赛时评级较高的选手胜出。因此,题目中的条件等价于:对任意 \(2\leq i\leq n\),\(|b_i - \max_{j < i} b_j| > k\)。
因为 \(a_n\) 和 \(a_{n - 1}\) 一定会比赛,所以当 \(a_{n - 1} + k \geq a_n\) 时,无解,答案为 \(0\)。
设 \(l_i\) 表示最大的 \(j\) 使得 \(a_j + k < a_i\),\(r_i\) 表示最小的 \(j\) 使得 \(a_i + k < a_j\)。
考虑钦定前缀最大值的位置 \(q_1, q_2, \cdots, q_c\) 计算对应排列方案数。对于 \(a_{q_i}\),位置大于 \(l_{q_i}\) 的 \(a\) 必须放在 \(a_{q_{i + 1}}\) 之后。从限制强到限制弱依次插入每个元素。
- 对于 \(q_c\),将 \(l_{q_c} + 1\sim n\) 不含 \(q_c\) 的所有位置放在 \(q_c\) 之后,方案数为 \((n - l_{q_c} - 1) !\)。
- 从 \(c - 1\) 到 \(1\) 枚举 \(i\),注意到 \(q_i \leq l_{q_{i + 1}}\)(否则不合法),所以相当于将 \(l_{q_i} + 1\sim l_{q_{i + 1}}\) 不含 \(q_i\) 的所有位置 \(S\) 放在 \(q_{i + 1}\) 之后,此时 \(l_{q_{i + 1}} + 1\sim n\) 不含 \(q_{i + 1}\) 的所有位置已经在 \(q_{i + 1}\) 之后。因此,考虑每个位置插在哪个元素后面,方案数为 \(n - l_{q_{i + 1}}\sim n - l_{q_i} - 2\) 的积。
- 最后将 \(1\sim l_{q_1}\) 放在 \(q_1\) 之后,方案数为 \(n - l_{q_1}\sim n - 1\) 的积。
- 整理,得方案数 \((n - 1)! \prod_{i = 1} ^ {c - 1} (n - l_{q_i} - 1) ^ {-1}\)。
设 \(f_i\) 表示 \(q_1 = i\) 的方案数之和,从后往前转移,前缀和优化即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
*1810. CodeTON Round 4 (Div. 1 + Div. 2, Rated, Prizes!)
A. Beautiful Sequence
检查是否存在 \(a_i \leq i\) 即可。
B. Candies
如果 \(n\) 是偶数显然无解。否则考虑倒推,恰有一个操作使得操作前也为奇数。
总操作次数 \(\mathcal{O}(\log n)\)。代码。
C. Make It Permutation
特判掉全删掉再加一个 \(1\) 的情况,最终排列长度一定是某个 \(a_i\),调整法易证。
排序后枚举 \(|p| = a_i\),容易算出需要删掉和加入多少个数。
时间复杂度 \(\mathcal{O}(n\log n)\)。代码。
D. Climbing the Tree
令 \(b\gets a - b\),即每天相对于前一天上升的距离。
根据 \(a, b, n\) 可以算出树高区间 \(((n - 2)b + a, (n - 1)b + a]\)。特别地,当 \(n = 1\) 时区间为 \([1, a]\)。
维护当前树高区间 \([L, R]\),加入一个区间时,若有交,则将 \([L, R]\) 变成它和加入区间的交,否则一定不合法。
查询即检查 \(h = L\) 和 \(h = R\) 的答案是否相同,若相同则输出,不相同则无法确定。
时间复杂度 \(\mathcal{O}(q)\)。代码。
E. Monsters
考虑从 \(a_s = 0\) 的点开始 BFS,维护每个连通块。每次从队列中取出一个连通块,按 \(a\) 从小到大的顺序枚举所有出边,若已连通则跳过,否则能合并则合并(即当前连通块大小不小于对应 \(a\) 值),不能合并说明接下来也不能合并,直接退出。若整个过程至少合并一次,则重新丢入队列。
启发式合并 set 维护当前连通块的所有出边,时间复杂度 \(\mathcal{O}(m\log ^ 2 m)\)。代码。
F. M-tree
考虑求一次答案。假设答案为 \(c\),维护 \(v\) 表示能接多少个叶子,初始值为 \(1\)。从 \(c - 1\) 枚举到 \(1\),每次先将 \(v\) 乘以 \(m\),然后减去等于当前枚举值的 \(a\) 的数量。若最终 \(v < 0\) 则答案大于 \(c\),否则答案不大于 \(c\)。
在 \(m\) 进制下观察整个过程,我们发现相当于求最小的 \(c\) 使得 \(\sum m ^ {a_i} \leq m ^ c\)。用线段树或 set(维护值相同的连续段)维护 \(\sum m ^ {a_i}\) 形成的 \(m\) 进制数即可。
时间复杂度 \(\mathcal{O}((n + q)\log n)\) 或 \(\mathcal{O}(n + q\log n)\)。代码。
G. The Maximum Prefix
直接正着推肯定不太行,因为枚举 \(k\) 再枚举 \(S\) 已经要 \(n ^ 2\),再加上 DP 时肯定要记录当前前缀和,肯定寄了。
那么唯一的办法就是将 \(h_S\) 直接融入 DP 值,也就是直接 DP 期望值。那我们在一开始肯定得区分不同的 \(h_S\),这就给予我们唯一的 DP 设计方案:设 \(f_{i, j, 0 / 1}\) 表示当前序列长度为 \(i\),还需要加上 \(j\) 才能达到 \(S\),以及是否达到过 \(S\)。转移即 \(f_{i, j, k} (1 - \frac {x_i}{y_i}) \to f_{i + 1, j + 1, k}\) 以及对于 \(j > 0\),\(f_{i, j, k} \frac {x_i} {y_i} \to f_{i + 1, j - 1, k \lor j = 1}\)。\(k\) 的答案即 \(\sum_j f_{k, j, 1}\)。
时间复杂度 \(\mathcal{O}(n ^ 2)\)。代码。
*H. Last Number
找点规律。
打表发现问题分成两部分:第一部分的 \(S_{\min} = i\),第二部分的 \(S_{\min}\) 等于上次操作的结果。设 \(p\) 为第一次 \(2S_{\min} \geq S_{\max}\) 的操作,那么 \(1\sim p\) 为第一部分,\(p + 1\sim n - 1\) 为第二部分。
设 \(r_i\) 表示第 \(i\) 次操作的 \(S_{\max}\),\(l_i\) 表示 \(S_{\min}\),\(d_i = r_i - l_i\),答案即 \(r_{n - 1} - (r_{n - 2} - (\cdots - (r_p - l_p)))\)。因为 \(l_p = p\),所以只要求 \(\sum_{i = p} ^ {n - 1} r_i(-1) ^ {n - 1 - i}\) ,这要求我们用优秀的方式描述 \(r_i\)。
在操作 \(1\sim p\) 的部分,\(l_i\) 递增,且 \(r_i\) 不降,所以一个数最多只会加入 \(S\) 一次。注意到第 \(i\) 次操作后所有 \(\geq d_i\) 的数不会再改变,设这些数为 \(T\)。考虑随着 \(i\) 增大 \(T\) 的变化情况:
- 若 \(r_i = r_{i - 1}\),相当于往 \(T\) 中加了两个 \(d_i\)。
- 若 \(r_i = r_{i - 1} - 1\),相当于往 \(T\) 中加了两个 \(d_i\) 和一个 \(d_i + 1\)。
设 \(s_i = r_{i - 1} - r_i\),那么 \(s_i = 0\) 相当于在 \(T\) 末尾加入 \(1, 0\),\(s_i = 1\) 相当于在 \(T\) 末尾加入 \(1, 1, 0\)。
不断进行操作,得到无限长度的字符串 \(s\) 形如 0 / 10 / 110, 10 / 110, 110, 10, 110, 10 / ...,其中每一层都是上一层的字符串的 0 变成 10,1 变成 110,然后拼接而成。设 \(h\) 表示 \(s\) 的前缀和,那么 \(r_i = n - h_i\)。
考虑答案式 \(n - h_{n - 1} - (n - h_{n - 2} - (\cdots - (n - h_p - p)))\)。
- 当 \(n - p\) 是偶数时,答案为 \(p - s_{n - 1} - s_{n - 3} - \cdots - s_{p + 1}\)。
- 当 \(n - p\) 是奇数时,答案为 \((n - h_p - p) - s_{n - 1} - s_{n - 3} - \cdots - s_{p + 2}\)。
问题转化为:给定前缀长度 \(p\),求 \(s\) 的前缀和,前缀奇数位置和,前缀偶数位置和。设 \(f_{i, j} = (a, b, c, d)\) 表示从 \(i\) 开始迭代 \(j\) 次,得到的字符串的长度,和,偶数位置和,奇数位置和。按顺序合并两个四元组 \((a_1, b_1, c_1, d_1)\) 和 \((a_2, b_2, c_2, d_2)\) 时:
- \(a = a_1 + a_2\)。
- \(b = b_1 + b_2\)。
- 当 \(a_1\) 为偶数时,\(c = c_1 + c_2\),否则 \(c = c_1 + d_2\)。
- 当 \(a_1\) 为偶数时,\(d = d_1 + d_2\),否则 \(d = d_1 + c_2\)。
预处理这些信息后容易做到单次查询 \(\mathcal{O}(\log n)\)。
二分求出 \(p\),容易通过 \(\mathcal{O}(1)\) 次查询求出答案。时间复杂度 \(\mathcal{O}(\log ^ 2n)\)。
\(p\) 可以类似查询的方式做到 \(\mathcal{O}(\log n)\) 计算。时间复杂度 \(\mathcal{O}(\log n)\)。代码。
实际上 \(s\) 就是斐波那契串,那么 \(r_i = n + 1 - \lceil\frac i {\phi} \rceil\)。将 \(\phi\) 用分数近似表示后转化为经典和式:扩展欧几里得。
*1811. Codeforces Round 863 (Div. 3)
G2. Vlad and the Nice Paths (hard version)
设 \(f_i\) 表示以 \(i\) 结尾的最长合法路径长度,\(g_i\) 表示对应方案数。
枚举 \(j < i\),要求 \(c_{j + 1\sim i}\) 至少出现 \(k\) 次 \(c_i\),用 \(f_j + 1\) 更新 \(f_i\)。
对所有 \(j < i\),设 \(c_i\) 在 \(c_{j + 1\sim i}\) 中出现 \(x\) 次,将 \(g_i\) 加上 \(g_j\binom {x - 1} {k - 1}\)。
时间复杂度 \(\mathcal{O}(n ^ 2)\)。代码。
*1814. Educational Codeforces Round 146
A. Coins
若 \(y\geq 2\),那么将 \(y\) 减去 \(2\),\(x\) 加上 \(k\) 一定合法。
检查 \(y = 0\) 和 \(y = 1\) 是否有解即可。
B. Long Legs
考虑枚举操作 \(3\) 的次数 \(c\),那么总操作次数为 \(c + \lfloor \frac x c\rfloor + \lfloor \frac y c\rfloor + [c\nmid x] + [c\nmid y]\)。
显然 \(c\) 不超过 \(\mathcal{O}(\sqrt n)\),直接枚举即可。
时间复杂度 \(\mathcal{O}(\sqrt n)\)。代码。
C. Search in Parallel
考虑若将 \(i\) 放在第 \(j\) 个机器人的序列的第 \(k\) 个位置,会产生代价 \(s_j \times k \times r_i\)。按 \(r_i\) 从大到小,每次将其贪心插到代价最小的机器人序列中,即 \((|a| + 1)s_1\) 和 \((|b| + 1)s_2\) 的较小值的对应序列。
时间复杂度 \(\mathcal{O}(n\log n)\)。代码。
*D. Balancing Weapons
若所有武器均被调整,则总存在方案:令 \(d_i = \prod f_{j\neq i}\) 即可。
否则至少一个武器被保留。直接枚举保留的武器 \(i\),那么其它武器 \(j\) 只有三种可能:
- 保留,代价为 \(0\)。
- 改成最大的 \(d_j\) 使得 \(d_jf_j\leq d_if_i\),代价为 \(1\)。
- 改成最小的 \(d_j\) 使得 \(d_jf_j \geq d_if_i\),代价为 \(1\)。
注意修改后的 \(d_j\) 必须大于 \(0\),所以一些情况是非法的。
总共 \(\mathcal{O}(n)\) 把武器,按 \(p\) 排序后双指针。若当前 \(l\sim r\) 之间所有原武器均出现,那么可用区间内只出现代价为 \(1\) 的武器的原武器的数量更新答案。
时间复杂度 \(\mathcal{O}(n ^ 2\log n)\),和 \(k\) 无关。代码。
利用 \(k\) 较小的性质容易做到 \(\mathcal{O}(n(n + k))\):只有 \([p_i - k, p_i + k]\) 的新武器有用,直接桶排即可。
E. Chain Chips
考虑到总可以调整使得一条边被经过两次,且与一个点相邻的两条边至少有一条要被经过两次,设 \(f_{i, j}\) 表示考虑到第 \(i\) 条边,\(j\) 是否被选择的最小代价,有 \(f_{i, 0} = f_{i - 1, 1}\),\(f_{i, 1} = \min(f_{i - 1, 0}, f_{i - 1, 1}) + 2a_i\)。动态 DP 即可。
注意第一条边和最后一条边一定要被选。
时间复杂度 \(\mathcal{O}(n + q\log n)\)。代码。
F. Communication Towers
考虑线段树分治,到每个叶子 \([x, x]\) 时,所有与 \(1\) 连通的信号站都可以收到信号。
合并 \(x, y\) 时,若 \(x, y\) 均不包含 \(1\),那么新建点 \(u\) 连向 \(x, y\)。若 \(x\) 包含 \(1\),则将 \(y\) 打上标记。若 \(y\) 包含 \(1\),则将 \(x\) 打上标记。最后从有标记的点开始可达的所有信号站就是答案。
时间复杂度 \(\mathcal{O}(m\log n\log r)\)。代码。
*1815. Codeforces Round 865 (Div. 1)
A. Ian and Array Sorting
做一次差分 \(d_i = a_i - a_{i - 1}\),那么操作相当于将 \(d_i\)(\(1\leq i < n\))加上任意整数 \(k\),\(d_{i + 2}\) 减去 \(k\)。目标序列满足 \(d_{2\sim n} \geq 0\),\(d_1\) 和 \(d_{n + 1}\) 可以任取。
因为所有偶数位置上的 \(d\) 和所有奇数位置上的 \(d\) 总和分别不变,所以若 \(n + 1\) 为偶数,那么一定可以达到目标,若 \(n + 1\) 为奇数,那么可行当且仅当 \(\sum_{2\leq 2k \leq n} d_{2k}\geq 0\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
B. Sum Graph
加入所有 \(i + j = n + 1\) 和 \(i + j = n + 2\) 的边,得到一条链。
任选一个 \(p_i\),得到 \(p_i\) 和所有 \(p_j\) 的距离 \(q(i, j)\),然后任选一个 \(q(i, j) = 1\) 的 \(p_j\),得到 \(p_j\) 和所有 \(p_k\) 的距离 \(q(j, k)\)。对于 \(q(i, j) + q(j, k) = q(i, k)\) 的 \(k\),和 \(j\) 在同一侧,否则在另一侧。根据得到的链,只有两种可能的排列,回答之。
总询问次数恰为 \(2n\)。代码。
C. Between
对限制 \((a_i, b_i)\),从 \(b_i\) 向 \(a_i\) 连有向边。对于所有有向边 \(x\to y\),若整个序列有 \(k\) 个 \(x\),那至多能有 \(k + 1\) 个 \(y\)。
考虑 \(1\) 到每个点的最短路 \(d_i\),若 \(1\) 不可达 \(i\),说明 \(i\) 的出现次数可以为无穷大。否则 \(i\) 至多出现 \(d_i + 1\) 次。
构造答案:从 \(1\) 到 \(n\) 枚举出现次数 \(j\),从 \(1\) 到 \(n\) 枚举每个点 \(i\),若 \(d_i + 1 \geq j\),则将 \(i\) 加入序列。
时间复杂度 \(\mathcal{O}(m + n ^ 2)\)。代码。
D. XOR Counting
\(m = 1\) 是平凡的。
\(m \geq 3\) 可以构造 \(x\)(\(x\equiv n\pmod 2\))和两个 \(\frac {n - x} 2\) 做到任意 \(n - 2k\)(\(0\leq 2k\leq n\))。
相当于求 \(x\oplus (n - x)\) 的所有可能的值之和。
数位 DP 记录一维表示下一位是否进位,枚举 \(x\) 和 \(n - x\) 的第 \(i\) 位,根据实际意义转移即可。
时间复杂度 \(\mathcal{O}(\log n)\)。代码。
*E. Bosco and Particle
很厉害的一道题目。
首先将每个串变成它的最小整周期串,那么就是要计算经过多长时间后,粒子再次回到 \(0\) 且所有对撞器的指针指向开头。
对于每个对撞器,其指针所跳过的 \(0\) 的数量决定了粒子的位置:若为偶数则在左侧,为奇数则在右侧。所以若串中 \(0\) 的数量为奇数,则需要倍长该串。
对每个对撞器,求出信息:每 \(x\) 次从左侧进入,将产生 \(y\) 次向右侧出发,其中 \(x\) 表示第 \(2k\) 个 \(0\) 到第 \(2k + 1\) 个 \(0\) 之间的字符数量,\(y\) 表示第 \(2k + 1\) 个 \(0\) 到第 \(2k + 2\) 个 \(0\) 之间的字符数量。
考虑从 \(0\) 出发的次数 \(z\),则 \(\frac z {x_1}, \frac {z y_1} {x_1x_2}, \frac {zy_1y_2} {x_1x_2x_3}, \ldots\) 均需要是整数。对所有 \(x, y\) 分解质因数,容易得到最小的 \(z\),进而得到循环节长度。
注意特判全 \(1\) 串,此时将其视为 \(n + 1\) 即可。
时间复杂度 \(\mathcal{O}(\sum |s_i|)\)。代码。
*F. OH NO1 (-2-3-4)
神必 MO 题。
设 \(f_i\) 表示 \(a_i\) 加上 \(i\) 的入度,考虑给每条边定向使得 \(f_i\) 互不相同。每次取出 \(f_i\) 最小的 \(i\),将与之相连的还没有定向的边指向对应邻居,这样未处理的点的 \(f\) 只会增大,符合限制。
每个三元环的贡献形如 \((0, 1, 2)\) 或 \((1, 1, 1)\),而在原问题上对三元环构造 \((3, 4, 5)\) 和 \((4, 4, 4)\) 是容易的。因此,将每个三元环上所有点的 \(a_i\) 加上 \(3\),然后做转化后的问题即可。
时间复杂度 \(\mathcal{O}(m\log m)\)。代码。
*1817. Codeforces Round 869 (Div. 1)
A. Almost Increasing Subsequence
答案为区间内属于某个长度大于 \(1\) 的上升子段的位置数量。若左端点不属于这样的位置,答案还要 \(+1\),右端点同理。
时间复杂度 \(\mathcal{O}(n + q)\)。代码。
*B. Fish Graph
枚举 \(u\),显然 \(u\) 的度数不小于 \(4\)。如果我们找到了经过 \(u\) 的环,考虑环上与 \(u\) 相邻两点 \(x, y\),加入 \(u\) 的两条非 \(x, y\) 出边 \(a, b\)。
且慢,万一 \(a, b\) 也在环上怎么办?调整成环 \(a \to u \to b \rightsquigarrow a\),然后加入 \((u, x)\) 和 \((u, y)\) 即可。
如何找经过 \(u\) 的环?这就是套路的积累了。
从 \(u\) 的所有出边开始 BFS,记录每个点是由哪个 \(u\) 的邻居达到的,设为 \(f_i\)。BFS 时,若遇到边 \((i, j)\) 满足 \(f_i \neq f_j\),则存在环 \(u\to f_i\rightsquigarrow i \to j \rightsquigarrow f_j \to u\)。为输出方案,记录每个点在 BFS 树上的父亲 \(fr_i\)。
然后我们发现,因为执行的是 BFS,所以找到的环的长度一定最小,也就是说,对于一开始的思路,\(a, b\) 不可能在环上,皆大欢喜。
时间复杂度 \(\mathcal{O}(nm)\)。代码。
直接找一个点双里的 \(u\) 即可做到 \(\mathcal{O}(n)\)。
*C. Similar Polynomials
多项式次数太高了,不好处理。考虑 “求导” 降次。离散意义下就是差分。
我们知道,对函数做形如 \(f'(x) \gets f(x + 1) - f(x)\) 的差分,则 \(\deg f' = \deg f - 1\)。所以将 \(d + 1\) 个点值差分 \(d - 1\) 次,\(A\) 从 \(d\) 次变成 \(1\) 次,也就是直线 \(A' = kx + b\)。
\(A(0\sim d)\) 的 \(d - 1\) 阶差分 \(a_0, a_1\) 分别等于 \(A'(0), A'(1)\),相当于 \(kx + b\) 在 \(x = 0\) 和 \(x = 1\) 处的点值。
\(B(0\sim d)\) 即 \(A(s\sim s + d)\) 的 \(d - 1\) 阶差分 \(b_0, b_1\) 分别等于 \(A'(s), A'(s + 1)\),相当于 \(kx + b\) 在 \(x = s\) 和 \(x = s + 1\) 处的点值。
显然,根据 \(a_0\) 和 \(a_1\) 可以直接确定直线,再代入 \((s, b_0)\) 或 \((s + 1, b_1)\) 即可。答案即 \(\frac {b_1 - a_1} {a_1 - a_0}\) 或 \(\frac {b_0 - a_0} {a_1 - a_0}\)。
至于 \(k\) 阶差分怎么求:
时间复杂度 \(\mathcal{O}(d)\)。代码。
D. Toy Machine
烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂。
烂烂 Ad-hoc。
对于 \(k = 2\),考虑把 \(1\) 搞到它后面,容易想到执行 LDRU,发现 \(2\sim \frac {n - 1} 2\) 向前移动了一位。因此,设 \(m = \frac {n - 1} 2\),对于 \(k\leq m\),执行 \(k - 1\) 次 LDRU 和一次 L。
那后半部分怎么办?考虑先用对称的方法将 \(k\) 挪到最右边,然后不断执行 RDRU 直到所有数全部堆在右半部分,且 \(k\) 在右上角,再执行一次 LU,\(k\) 就变到了原来 \(m\) 的位置。
时间复杂度 \(\mathcal{O}(n)\)。代码。
*E. Half-sum
不妨设 \(A < B\),则一组方案的权值为 \(B - A\)。
考虑最终变成 \(A\) 和 \(B\) 的所有数 \(A_{1\sim a}\) 和 \(B_{1\sim b}\)(\(a, b > 0\)),从小到大排序。设 \(A_i\) 被合并 \(c_i\) 次,\(B_i\) 被合并 \(d_i\) 次,则 \(B - A\) 等于
观察样例 \(4\),发现 \(59\) 是 \(\frac {16 + 32} 2 = 24\),\(\frac {24 + 64} 2 = 44\),\(\frac {44 + 64} 2 = 54\),\(\frac {54 + 64} 2 = 59\) 这样得来的,这启发我们猜想:对于 \(B\),一定是先合并 \(B_1, B_2\) 得到 \(D_2\),再合并 \(D_2, B_3\) 得到 \(B_3\),以此类推。对于 \(A\),一定是先合并 \(A_a, A_{a - 1}\) 得到 \(C_{a - 1}\),再合并 \(C_{a - 1}, A_{a - 2}\) 得到 \(C_{a - 2}\),以此类推。
证明:
对于四个数 \(e \leq f\leq g\leq h\),不妨设它们属于 \(B\),那么合并 \(e, f\),再将得到的数合并 \(g\),再将得到的数合并 \(h\),一定不劣于将 \(e, f, g, h\) 分成两组,两两合并后再合并。对于前者,贡献为 \(\frac e 8 + \frac f 8 + \frac g 4 + \frac h 2\),对于后者,贡献为 \(\frac {e + f + g + h} 4\)。因为 \(2h\geq e + f\),所以 \(\frac h 4 \geq \frac e 8 + \frac f 8\)。这说明:\(D_i\) 不会由 \(D_j\) 和 \(D_k\) 合并而来(\(j, k < i\))。
因此 \(d_i\) 形成的可重集形如 \(\{1, 2, \cdots, b - 2, b - 1, b - 1\}\),将较小的 \(c_i\) 分给较大的 \(b_i\) 一定更优。调整法易证。
综上,\(D_2 = \mathrm{merge}(B_1, B_2)\),对于 \(i > 2\),\(D_i = \mathrm{merge}(D_{i - 1}, B_i)\)。
对于 \(A\),同理。\(\square\)
有了该结论,若存在 \(A_i > B_j\),则交换 \(A_i, B_j\) 更优,因为减数变小了,加数变大了。
这说明将 \(a\) 排序后存在 \(2\leq i\leq n\) 使得 \(a_{1\sim i - 1}\) 合并至 \(A\),\(a_{i\sim n}\) 合并至 \(B\)。
至此可以做到 \(\mathcal{O}(n ^ 2)\):枚举 \(i\),计算 \(B - A\),用二进制高精度表示,形如 \(X_i = \sum_{i = 0} ^ n \frac {x_i} {2 ^ i}\)。求出 \(X_i\) 的最大值。
遇到这种 \(2\) 的幂的情况,通常都会根据 \(2\) 的幂的性质(\(\sum_{i = 0} ^ {n - 1} 2 ^ i < 2 ^ n\)),将某些范围限定在 \(\log\) 值域的大小(数位 DP 经常用到这一点)。
考虑 \(i\to i + 1\),把式子写下来发现 \(X_{i + 1} - X_i = \Delta_{i\to i + 1} = \frac {a_{i + 1} - a_i} {2 ^ {n - i}} - \frac {a_i - a_{i - 1}} {2 ^ {i - 1}}\)。这说明对于 \(a_i = a_{i - 1}\) 的 \(i\),\(X_i\leq X_{i + 1}\),\(X_i\leq X_{i - 1}\),即若 \(a_i = a_{i - 1}\),那么在 \(i - 1\sim i\) 之间切一刀一定不优。除非所有数相等,此时答案为 \(0\)。
进一步探索,对 \(a\) 差分得到 \(b\)(\(b_i = a_i - a_{i - 1}\)),对于 \(i\to j\),有
当 \(i < j \leq \frac n 2\) 时, \(b_j\) 的系数是负数。如果 \(\frac {b_i} {2 ^ {i - 1}} \geq \frac {b_j} {2 ^ {n - j + 1}}\),那么 \(\Delta_{i\to j} \leq 0\),\(j\) 一定不优。因为 \(b \leq 10 ^ 9\) 且 \(n - j + 1\geq \frac n 2\),所以只要 \(b_i > 0\) 且 \(i \leq \frac n 2 - 30\),就有 \(\Delta_{i\to j}\leq 0\)。
因此,找到第一个使得 \(b_i > 0\) 且 \(i\leq \frac n 2 - 30\) 的 \(i\),\(i\) 在前半部分一定更优。若不存在,检查 \(\frac n 2 - 30\leq i \leq \frac n 2\)。对于右半部分同理。
一个等价的实现是:找到前 \(30\) 和后 \(30\) 个 \(a_{i - 1} \neq a_i\) 的位置,检查之。
时间复杂度 \(\mathcal{O}(n\log a_i)\)。代码。
官方题解给出了妙妙分治做法:在 \([l, r]\) 寻找最优决策点时,\(a_{1\sim l - 2}\) 和 \(a_{r + 2\sim n}\) 的系数不变,只关心 \(a_{l - 1\sim r + 1}\),可以做到 \(\mathcal{O}(\mathrm{len})\) 比较左子区间和右子区间哪个更优。时间复杂度 \(\mathcal{O}(n\log n)\)。将该思想应用于上述做法,可得 \(\mathcal{O}(n + \log a_i \log\log a_i)\) 解法,但读入信息量为 \(\mathcal{O}(n\log a_i)\)。
F. Entangled Substrings
建出基本子串结构,\(a, b\) 合法当且仅当它们不重叠且属于相同等价类。
问题相当于求一个左边界和上边界对齐阶梯型内有多少点对 \(P, Q\) 满足 \(y_P < x_Q\)。枚举 \(x_Q\),用单指针求出有多少 \((x_Q, y)\),使得 \(y_P < x_Q\) 的 \((x, y_P)\) 数量也容易前缀和求出。
时间复杂度 \(\mathcal{O}(n|\Sigma|)\)。代码。
*1819. Codeforces Round 866 (Div. 1)
A. Constructive Problem
求出 \(v = \mathrm{MEX}(a)\),若 \(v = n\) 显然无解。
否则,若 \(v + 1\notin a\),显然有解。
否则 \([l, r]\) 一定要包含 \(v + 1\) 的所有出现。感性理解区间越小越好,所以将 \(a_{l\sim r}\) 赋值为 \(v\),检查是否有 \(v + 1 = \mathrm{MEX}(a')\) 即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
B. The Butcher
考虑逆推。
先算出面积 \(S = \sum a_i b_i\) 以及 \(A = \max a_i\) 和 \(B = \max b_i\)。那么形状只有可能是 \(A\times \frac S A\) 或 \(\frac S B\times B\)。
检查 \(x\times y\) 是否为答案是容易的:每次必然切掉一边,按 \(a_i\) 和 \(b_i\) 分别从大到小排序后用两个指针维护即可。
时间复杂度 \(\mathcal{O}(n\log n)\)。代码。
C. The Fox and the Complete Tree Traversal
先把 \(n = 2\) 的平凡情况特判掉,否则选一个非叶子作为根。
对点 \(i\),考虑环在 \(i\) 子树内的部分,发现必然是一段,因为进去再出来再进去再出来是不可能的。因此,设 \(i\) 子树的插头为 \(x, y\),其中必然有一个是 \(i\),另一个是 \(i\) 的儿子,设为 \(f_i\)。当 \(i\) 为叶子时 \(f\) 不存在。
合并 \(i\) 的所有儿子时,若 \(i\) 有两个儿子 \(f_u\) 非空,因为 \(f_u\) 只能跳到 \(i\),所以当且仅当 \(i\) 为根时合法:若 \(i\) 非根,因为根不是叶子,所以则 \(i\) 子树外必然有一个距离 \(i\) 为 \(2\) 的插头,这个插头只能跳到 \(i\)。
对于非叶子:
- 若所有儿子 \(f\) 为空,则连接 \(i\) 和任意儿子,并将剩下所有儿子串起来,令 \(f_i\) 为最后一个儿子。
- 若存在一个儿子 \(f\) 非空,则从该儿子开始将剩下所有儿子串起来,令 \(f_i\) 为最后一个儿子。
- 若存在两个儿子 \(f\) 非空,若非根则无解,否则从其中一个儿子开始,另一个儿子结束将所有儿子串起来。
- 若存在大于两个儿子 \(f\) 非空,无解。
- 特别地,将所有 \(f\) 非空的儿子的 \(f\) 和 \(i\) 直接相连。
最终得到以根为端点的链或一条环。从根开始在环上遍历即可。
细节较多。时间复杂度 \(\mathcal{O}(n)\)。代码。
实际上,一棵树合法当且仅当它是毛毛虫,将度数为 \(1\) 的点处理掉,剩下一条链,处理一下即可。
D. Misha and Apples
将商店卖的苹果种类看成集合 \(S_i\),设 \(f_i\) 表示最小的 \(j\) 使得编号为 \(f_i\sim j\) 的集合都可以被保留。
考虑转移,显然 \(f_{i - 1}\leq f_i\)。
- 若 \(k_i = 0\),则令 \(S_i = \varnothing\) 即可使 \(f_i = f_{i - 1}\)。
- 若 \(k_i > 0\),考虑最大的 \(p < i\) 使得 \(S_p\) 和 \(S_i\) 有交。若不存在,则 \(f_i = f_{i - 1}\)。否则若此时 \(S_p\) 仍未被删去,则整个背包就空了。
- 若 \(p < f_{i - 1}\),\(p\) 无论如何一定被删去,\(f_i = f_{i - 1}\)。
- 若 \(p\geq f_{i - 1}\) 就不太好办了。发现此时 \(f_i\) 等于最小的 \(q + 1\),满足 \(p\leq q\) 且存在一种方案使得 \(S_q\) 之后整个背包为空。
因此,设 \(g_i\) 表示是否存在一种方案使得处理 \(S_i\) 之后整个背包为空。
- 若 \(k_i = 0\),总可以使得背包为空:若处理 \(S_i\) 之前背包为空,则令 \(S_i = \varnothing\);否则令 \(S_i\) 为之前的背包。故 \(g_i = 1\)。
- 若 \(k_i > 0\),如果 \(f_{i - 1}\sim i - 1\) 之间有 \(k_j = 0\),则可以通过合理地设置 \(S_j\) 清空背包,\(g_i = 1\)。否则考虑最大的 \(p < i\) 使得 \(S_p\) 和 \(S_i\) 有交。若不存在,显然 \(g_i = 0\)。
- 若 \(p < f_{i - 1}\),则无论如何 \(S_i\) 无法被删去,\(g_i = 0\)。
- 若 \(p \geq f_{i - 1}\),则 \(S_i\) 可以通过 \(S_p\) 将整个背包清空,\(g_i = 1\)。
用 set 维护所有 \(g_i = 1\) 的 \(i\),时间复杂度 \(\mathcal{O}(n\log n + \sum k_i)\)。
每次查询 lower_bound 之后 \(f\) 值变成对应后继加 \(1\),具有单调性,直接双端队列维护。
若 \(f_n\sim n\) 之间有 \(k_i = 0\),显然答案为 \(m\)。否则答案为之间的 \(k_i\) 之和。
时间复杂度 \(\mathcal{O}(n + \sum k)\)。注意清空的复杂度,因为 \(\sum m\) 没有保证。代码。
*E. Roads in E City
考虑删边,删去 \((u_i, v_i)\) 后随机询问 \(45\) 次 \(u_i\) 或 \(v_i\),若 \(u_i, v_i\) 不连通,则有极大概率得到至少一个 \(0\)。否则所有询问均返回 \(1\)。由此求出任意一棵被修复的边的生成树。
接下来考虑每条非树边 \((u_i, v_i)\),删去 \(u_i, v_i\) 树上简单路径上任意一条边 \((u_j, v_j)\),然后加入 \((u_i, v_i)\),随机询问 \(45\) 次 \(u_i\) 或 \(v_i\),可以以极大概率求出 \((u_i, v_i)\) 是否被修复。原理是一样的。
正确率为 \(1 - \frac 1 {2 ^ k}\),其中 \(k = 45\)。代码
*F. Willy-nilly, Crack, Into Release!
变换规则太复杂了,但是有一点很显然:若 \(s\) 经过一次变换得到 \(t\),\(t\) 也可以经过一次变换得到 \(s\)。
这启发我们把所有字符串以及它们之间通过单次变换互相转化的关系抽象成图,然后研究图具有的性质,因为在图上更容易看出一些仅通过字符串和复杂的变换难以发现的性质和模式。从这点来看,抽象成图反而让这道题目更加具象,而思考问题越具象,思路就越流畅,这就是为什么举例子是一个很好的说明方式。
言归正传。从小规模的图入手,因为大规模的图处理起来较复杂。
对于 \(n = 1\),很显然,图是一个正方形。不妨认为左上角是 \(a\),左下角是 \(b\),右下角是 \(c\),右上角是 \(d\)。
对于 \(n = 2\),事情变得有趣起来了。\(a*, b*, c*, d*\) 分别构成了 \(n = 1\) 的正方形,但 \(ab\) 和 \(ba\),\(ad\) 和 \(da\),\(bc\) 和 \(cb\),\(cd\) 和 \(dc\) 之间也有连边。将 \(a*\) 代表的正方形放在左上角,\(b*\) 放在左下角,\(c*\) 放在右下角,\(d*\) 放在右上角,那么整个结构形如四个角都被标上直角符号的正方形。
对于 \(n = 3\),有了先前的思考,我们猜测图张成这样:将 \(n = 2\) 的四张图按照上文提到过的顺序排列,然后在 \(abb\) 和 \(baa\),\(add\) 和 \(daa\),\(bcc\) 和 \(cbb\),\(bdd\) 和 \(dbb\) 之间连边,形成分形结构。
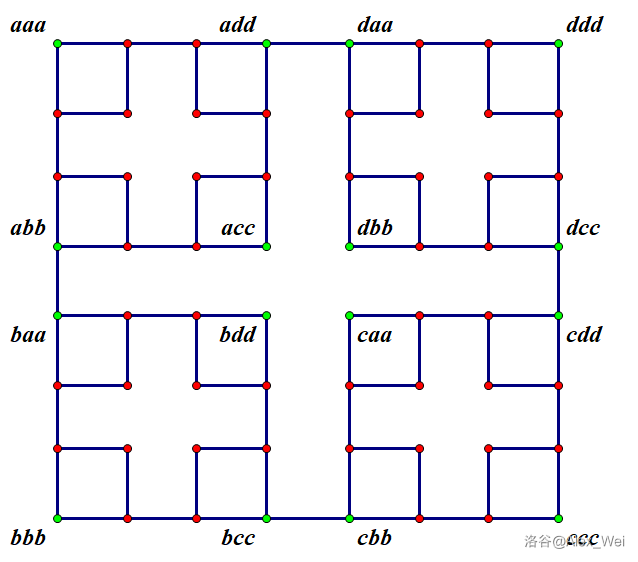
这张图也很好理解:如果想要改变 \(s_1\),那么 \(s_2\sim s_n\) 必须相同。
到这里思路就很清晰了。
我们建出所有字符串的字典树,深度为 \(i\) 的结点(根节点深度为 \(0\))对应大小为 \(n - i\) 的分型结构。一个分形结构在比它大一级的结构中,只有四个端点是有用的。因此,设 \(f_{i, j, k}\) 表示在字典树结点 \(i\) 对应的分形结构中,从全是 \(j\) 的字符串走到全是 \(k\) 的字符串的 经过结构内所有关键点 的最短路,即任意两个端点之间的合法最短路。设 \(g_{i, j, k}\) 表示最长路。
根据实际意义转移即可,要求没有被经过的子结构内没有关键点。
例如,设 \(A, B, C, D\) 分别表示对应儿子,则:
- 令 \(f_{i, a, b} = f_{A, a, d} + f_{D, a, c} + f_{C, b, d} + f_{B, b, c} + 3\)。
- 如果 \(C\) 和 \(D\) 内没有关键点,则还可以用 \(f_{A, a, b} + f_{B, a, b} + 1\) 更新 \(f_{i, a, b}\)。
再记 \(F_i\) 和 \(G_i\) 表示经过结构内所有关键点的环。如果恰好一个结构内有关键点,则 \(F, G\) 可以直接继承对应结构的 \(F, G\)。还可以用 \(f_{A, b, d} + f_{D, a, c} + f_{C, b, d} + f_{B, a, c} + 4\) 更新 \(F\),\(G\) 同理。
实现时,可以将 \(f, g\) 绑定在一起减少讨论。
注意当 \(|S| < 2\) 时最小环为 \(2\)。当 \(|S| = 2\),集合内两个字符串相邻时最小环也为 \(2\)。为此,用 set 维护 \(S\)。
时间复杂度 \(\mathcal{O}(nq\log q)\),做到 \(\mathcal{O}(nq)\) 是平凡但不必要的。代码。
*1821. Educational Codeforces Round 147
A. Matching
若 \(s_0 = 0\) 则无解。
否则对于每个问号,若其位置为 \(0\),则产生 \(9\) 的贡献,否则产生 \(10\) 的贡献。
代码。
B. Sort the Subarray
找到包含 \(a_i \neq a'_i\) 的位置的 \(a'\) 的极长不降子段即为答案。
代码。
C. Tear It Apart
直接枚举最后剩下来哪个字符,考虑不包含该字符的最长子串长度 \(L\),若 \(L = 0\) 则代价为 \(0\),否则代价为 \(\lfloor \log_2 L\rfloor + 1\)。
所有字符代价取 \(\min\) 即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
*D. Black Cells
将贡献拆成两部分:最后停下来的位置,加上两倍覆盖的区间数量。
只有 \(l_i = r_i\) 的段可能跳过,因为跳过 \(l_i < r_i\) 的段,虽然减少了一次 Shift 和 Release,但是至少增加了两次 Move,一定不优。
考虑枚举最后一段 \(I_i\),设 \(I_{1\sim i - 1}\) 长度为 \(1\) 的区间数量为 \(c\),长度大于 \(1\) 的区间总长为 \(t\),区间数量为 \(u\)。
当 \(t + |I_i| \geq k\) 时,不用任何长度为 \(1\) 的区间,最后停在位置 \(l_i + k - t - 1\),区间数量为 \(u + 1\),且容易证明再往后枚举 \(i\) 一定不优。
否则,当 \(t + |I_i| + c \geq k\) 时,一定是 \(I_i\) 占满到 \(r_i\)(否则就落在上一个情况了),最后停在位置 \(r_i\),区间数量为 \(u + 1 + (k - t - |I_i|)\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
E. Rearrange Brackets
一个括号序列的代价是建树后所有点的深度之和。
把一个左括号挪到对应右括号左边,代价减小距离除以 \(2\)。用栈求出每对括号之间的距离,排序后选前 \(k\) 大即可。
时间复杂度 \(\mathcal{O}(n\log n)\) 或 \(\mathcal{O}(n)\)。代码。
*F. Timber
好题。
从左往右枚举,一棵树能往左倒就往左倒。
设 \(f_{i, j}\) 表示第 \(i\) 棵树倒下的右边界为 \(j\),那么对于 \(k + 1\leq p \leq 2k\),\(2f_{i, j}\to f_{i + 1, j + p}\),因为左端点和右端点都可以倒。对于 \(2k < p\),\(f_{i, j} \to f_{i + 1, j + p}\)。
问题转化为:选择 \(m\) 个数 \(x_i \geq k + 1\) 且 \(\sum x_i\leq n\),求所有方案的 \(\prod (1 + [x_i \leq 2k])\) 之和。
将 \(n\) 减去 \(m(k + 1)\),转化为 \(x_i \geq 0\) 和 \(\prod (1 + [x_i < k])\)。
注意到容易钦定 \(x_i \geq k\),所以钦定 \(c\) 个 \(x_i\geq k\),插板法得方案数为 \(g_c = \binom m c\binom {(n - ck - 1) + (m + 1)} {m}\),则 \(g_c = \sum_{i = c} ^ m \binom i c f_i\),其中 \(f_c\) 表示恰好 \(c\) 个 \(x_i\geq k\) 的方案数。
二项式反演得 \(f_c = \sum_{i = c} ^ m (-1) ^ {i - c} \binom i c g_i\),则答案为
时间复杂度 \(\mathcal{O}(n)\)。代码。
*1822. Codeforces Round 867 (Div. 3)
G2. Magic Triples (Hard Version)
设 \(c_i\) 表示 \(o\) 的出现次数。
对于 \(b = 1\),答案为 \(\sum c_i ^ {\underline{3}}\)。
对于 \(b > 1\),枚举 \(a_j\),考虑其所有非 \(1\) 因数 \(b\mid a_j\),将 \(c_{\frac {a_j} b}c_{a_j} c_{a_jb}\) 加入答案。
时间复杂度 \(\mathcal{O}(na ^ {\frac 1 3}\log n)\):对于 \(a_j > 10 ^ 6\),\(a_jb\leq 10 ^ 9\) 的 \(b\) 不超过 \(10 ^ 3\);对于 \(a_j\leq 10 ^ 6\),因数个数不超过 \(2\times 10 ^ 3\)。直接根据 \(d(n)\sim \mathcal{O}(n ^ {\frac 1 3})\) 可得同样复杂度,但跑不满,可以通过。代码。
直接枚举 \(a_k\),那么 \(b\) 的数量等于 \(a_k\) 的平方因子数量,即 \(d(n ^ {\frac 1 2}) \sim \mathcal{O}(n ^ {\frac 1 6})\)。时间复杂度 \(\mathcal{O}(na ^ {\frac 1 6}\log n)\)。
可以通过哈希表将 \(\log\) 因子去掉。
*1823. Codeforces Round 868 (Div. 2)
A. A-characteristic
枚举 \(1\) 的数量 \(c\),则权值为 \(\binom {c} 2 + \binom {n - c} 2\)。
检查是否存在 \(c\) 使得权值为 \(k\) 即可。
时间复杂度 \(\mathcal{O}(n)\)。代码。
B. Sort with Step
将下标和 \(p\) 均减去 \(1\),因为排序过程不改变下标模 \(k\) 相同的位置的元素集合,所以答案为 \(0\) 当且仅当 \(p_i\equiv i\pmod k\)。
若存在两个不符合的元素,交换它们可符合条件,答案为 \(1\)。
否则答案为 \(-1\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
C. Strongly Composite
对于三个不同的质数,\(abc\) 和 \(a ^ 2\) 都是合法的。设质数 \(i\) 在 \(\prod a\) 的幂次为 \(c_i\),那么先贪心地不断将 \(i ^ 2\) 加入 \(b\),最后剩下若干 \(c_i\) 为奇数的质数 \(i\),不断任选三个相乘加入 \(b\) 即可。答案即 \(\sum \lfloor \frac {c_i} 2 \rfloor + \lfloor \frac {\sum (c_i\bmod 2)} 3 \rfloor\)。
容易证明这是正确的。
时间复杂度 \(\mathcal{O}(n\sqrt a_i)\)。代码。
D. Unique Palindromes
考虑一个回文串第一次产生贡献的位置,那么这些位置互不相同。
对于相邻两个限制 \(i\sim i + 1\),若 \(x_{i + 1} - x_i < c_{i + 1} - c_i\) 显然无解。否则选连续 \(c_{i + 1} - c_i\) 个位置填入第 \(i + 3\) 个小写字母。
对于其它不产生贡献的位置,填入 abc 循环,那么只有开头的三个位置会产生贡献。注意到 \(x_1, c_1\geq 3\),故可行。
时间复杂度 \(\mathcal{O}(n)\)。代码。
E. Removing Graph
度数为 \(2\) 的图由若干个环组成。
设 \(f_i\) 表示长度为 \(i\) 的链的 SG 值,\(g_i\) 表示长度为 \(i\) 的环的 SG 值,打表发现当 \(i < l\) 或 \(i\geq l + r\) 时,SG 值为 \(0\),当 \(l\leq i < l + r\) 时,SG 值为 \(\lfloor\frac i l\rfloor\)。
实际上可以直接分析:因为 \(l < r\),所以对于 \(f_i\) 且 \(i \geq l\),总存在方案使得删去链后两侧长度相等,所以 \(f_i > 0\)。由此容易证明对于 \(i \geq l + r\) 有 \(g_i = 0\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
F. Random Walk
以 \(t\) 为根,找包含 \(s\) 的子树,其它部分删去。
每次进入一个点,我们可以认为对该点的子树进行深搜,然后返回其父亲。那么点 \(i\) 的答案为其度数乘以 \(t\to i\) 和 \(t\to s\) 的公共长度。
特判 \(t\) 的答案为 \(1\)。
时间复杂度 \(\mathcal{O}(n)\)。代码。
*1824. Codeforces Round 872 (Div. 1)
A. LuoTianyi and the Show
将大于 \(0\) 的数去重。
设 \(-1, -2\) 和大于 \(0\) 的数量分别为 \(x, y, z\)。
若第一次选择了 \(-1\),那么接下来只能选择 \(-1\) 或大于 \(0\),贡献为 \(\min(m, x + z)\)。
同理,若第一次选择了 \(-2\),则贡献为 \(\min(m, y + z)\)。
否则枚举第一次选择哪个大于 \(0\) 的数 \(x_i\),设它在所有大于 \(0\) 的数中的排名为 \(r\),则左边贡献为 \(\min(x_i - 1, r - 1 + x)\),右边贡献为 \(\min(m - x_i, z - r + x)\)。
时间复杂度 \(\mathcal{O}(n\log n)\) 或 \(\mathcal{O}(n + m)\)。代码。
B2. LuoTianyi and the Floating Islands (Hard Version)
\(k\) 为奇数时重心唯一,答案为 \(1\)。
\(k\) 为偶数时,若重心唯一,则产生 \(1\) 的贡献;若重心不唯一,则产生两重心之间最短路径长度的贡献。对于后者,枚举每条边,它产生贡献当且仅当两侧分别选择 \(\frac k 2\) 个点,方案数容易计算。最后给期望加上 \(1\) 即可。
预处理阶乘和阶乘逆元,时间复杂度 \(\mathcal{O}(n)\)。代码。
C. LuoTianyi and XOR-Tree
设 \(f_{i, j}\) 表示 \(i\) 到叶子所有路径异或和为 \(j\) 的最小代价,则先令 \(f_{i, j} = \sum_{u\in \mathrm{son}(i)} f_{u, j}\),然后将 \(f_{i, j}\) 的所有 \(j\) 同时异或 \(a_i\),最后将 \(f_{i, j}\) 和 \(\min_{k} f_{i, k} + 1\) 取最小值。
这说明 \(f_i\) 的极差不超过 \(1\)。维护 \(v_i\) 表示 \(\min_j f_{i, j}\),\(S_i\) 表示取到 \(v_i\) 的 \(j\) 的集合,则:
- 第一步操作相当于合并所有 \(S_u\) 到 可重集 \(S\)。
- 第二步直接打懒标记,设 \(c_i\) 表示 \(S_i\) 所有数要异或 \(c_i\) 才是真实值。
- 第三步设 \(S\) 最大出现次数为 \(\mathrm{occ}\),若 \(\mathrm{occ} = 1\),则 \(S_i = S\),否则 \(S_i\) 为 \(S\) 内取到最大 \(\mathrm{occ}\) 的所有数。对于后者,每个数出现次数至少减半,所以暴力遍历即可。
- 此外,\(v_i\) 即 \(\sum v_u + |\mathrm{son}(i)| - \mathrm{occ}\),\(c_i\) 变成 \(c_i\oplus a_i\)。
- 对于叶子,令 \(S_i = \{c_i\}\),\(v_i = 0\)。
启发式合并维护 \(S\),时间复杂度 \(\mathcal{O}(n\log ^ 2 n)\)。代码。
D. LuoTianyi and the Function
从右往左扫描线,对于 \(a_i\) 和它下一次出现的位置 \(j\),有
线段树维护区间赋值区间历史和即可。
时间复杂度 \(\mathcal{O}((n + q)\log n)\)。代码。
*E. LuoTianyi and Cartridge
\(\min(A, C)\) 不好处理,枚举之,设为 \(x\)。称一个点或一条边合法当且仅当 \(a_i\) 或 \(c_i\) 不小于 \(x\)。
先考虑对某个 \(v\) 求答案。显然,若一条边一侧没有被选中的点,则该边一定不会被选中。反之,若每条被选中的边两侧均有被选中的点,则一定合法:按任意顺序加入选中的边,其两侧必然存在被选择的 \(u, v\) 不连通,否则 \(T'\) 已经形成一个连通块,矛盾。
将不合法的边两端合并起来,得到一棵树 \(G\),树上每条边代表一条合法边,每个点代表若干个点(可以全都是非法点),且叶子对应至少一个合法点:若叶子不对应任何合法点,则将其和与其相连的唯一的边删去不影响答案,因为该边不可能被选中。
此外,一个叶子至少有一个点被选中,否则与其相连的唯一的边无法被选中,往 \(T'\) 加入该边和叶子内任意合法点,方案仍合法且权值增大。
因此,对于固定的 \(x = \min(A, C)\),可以算出 \(T'\) 的边数 \(e = \min(|V| - 1, |E|)\),其中 \(V, E\) 是删去了不合法的元素的点集和边集。
- 选点:选择所有叶子的权值最大的合法点,以及其它所有合法点的权值前 “\(e + 1\) 减去叶子数量” 大的点。
- 选边:选择权值前 \(e\) 大的合法边。
考虑实时维护 \(G\):
- 对每个点 \(u\in V_G\),记录 \(S_u\) 表示对应所有合法点的权值。
- 对每个点 \(u\in V_G\),记录 \(X_u\) 表示它在树上的所有邻边。
- 维护所有叶子权值最大的合法点的点权之和 \(L\)。
- 维护所有合法边权值构成的权值线段树 \(T_D\)。
- 维护所有合法点去掉每个叶子权值最大的合法点的点权构成权值线段树 \(T_B\)。
- 一个点是叶子当且仅当 \(|X_u| = 1\)。
考虑 \(x\) 在增大的过程中,会删去一些边或一些点。
对于删边,直接合并两侧的点,注意 \(S\) 和 \(X\) 需要启发式合并。
对于删点,若删去后得到了空叶子,则删除该叶子和与其相连的唯一的边。注意这个过程可能引发连锁反应(一个空心非叶子是合法的,所以删边可能导致某个空心非叶子变成空心叶子),用队列维护。
注意特判 \(|T'| = 1\) 的情况。
时间复杂度 \(\mathcal{O}(n\log ^ 2 n)\) 或 \(\mathcal{O}(n\log n)\)(线段树合并维护 \(S\),\(X\) 可以额外维护度数并懒惰删除将 set 换成 vector)。代码。