526互联

EulerNet Adaptive Feature Interaction Learning via Euler’s Formula for CTR Prediction

发布时间 2023-06-19 14:52:11作者: 馒头and花卷

目录

Tian Z., Bai T., Zhao W., Wen J. and Cao Z. Eulernet: Adaptive feature interaction learning via euler’s formula for ctr prediction. SIGIR, 2023.

概

一种能够自适应地学习阶数地网络.

Motivation

  • 高阶信息, 对于 CTR 任务而言是十分重要的, 之前的方法, 通常需要我们显式地构造这种信息:

    \[\Delta_{ex} = \sum_{\alpha \in \mathcal{A}} \bm{e}_1^{\alpha_1} \odot \bm{e}_2^{\alpha_2} \odot \cdots \odot \bm{e}_m^{\alpha_m}, \]

    其中 \(\bm{\alpha} = [\alpha_1, \alpha_2, \ldots, \alpha_m]\) 是不同的阶数.

  • 为了充分利用高阶信息, 我们可能需要合理地设计 \(\mathcal{A}\), 而这通常是困难的. 我们需要一种能够自适应的学习方式来处理.

Eulernet

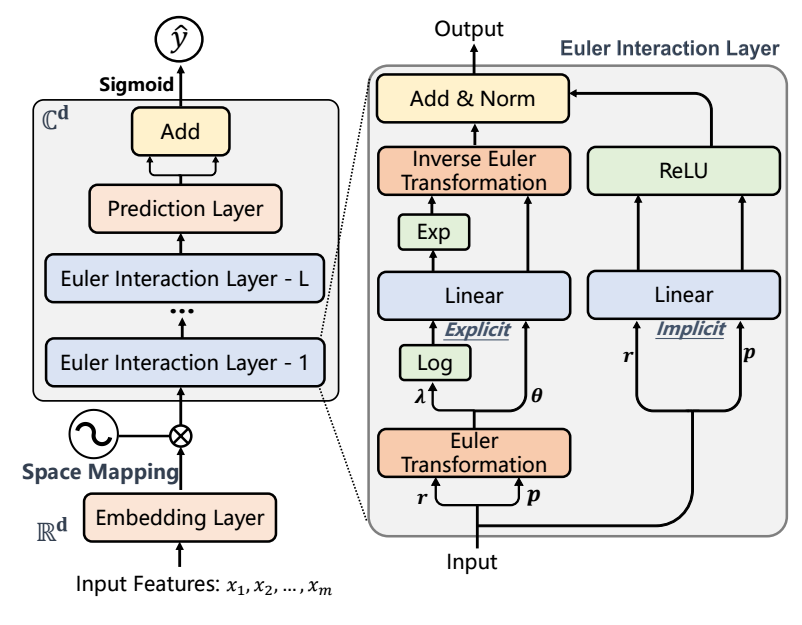
  • Eulernet 主要是 Euler Interaction Layer 的设计.

Explict

  • 每一层的输入为:

    \[\bm{r}_j + i \bm{p}_j \]

    对于最初输入, \(\bm{r}_j = \mu_j \cos(\bm{e}_j), \quad \bm{p}_j = \mu_j \sin (\bm{e}_j)\), 其中 \(\mu_j\) 亦为可学习的参数.

  • 我们知道, 对于

    \[\tilde{\bm{e}}_j = \bm{r}_j + i \bm{p}_j = \bm{\lambda}_j e^{i \bm{\theta}_j}, \]

    其中 (我们可以通过极坐标变换得到)

    \[\bm{\lambda}_j = \sqrt{\bm{r}_j^2 + \bm{p}_j^2}, \bm{\theta}_j = \text{atan2}(\bm{p}_j, \bm{r}_j), \]

    atan2 是反三角函数.

  • 我们希望得到高阶信息 (先考虑一个 \(\alpha\)):

    \[\Delta_{ex} = \tilde{\bm{e}}_1^{\alpha_1} \odot \tilde{\bm{e}}_2^{\alpha_2} \odot \cdots \odot \tilde{\bm{e}}_m^{\alpha_m}, \]

    可以发现:

    \[\begin{array}{ll} \Delta_{ex} &= \tilde{\bm{e}}_1^{\alpha_1} \odot \tilde{\bm{e}}_2^{\alpha_2} \odot \cdots \odot \tilde{\bm{e}}_m^{\alpha_m} \\ &= \prod_{j=1}^m (\bm{\lambda}_j^{\alpha_j} \exp(i \alpha_j \bm{\theta}_j)) \\ &= \exp(\sum_{j=1}^m \alpha_j \log (\bm{\lambda}_j)) \exp(i \sum_{j=1}^m\alpha_j \bm{\theta}_j)). \\ \end{array} \]

    如此一来乘法就全部变成加法了 (好处?)

  • 若令

    \[\bm{\psi}_k = \sum_{j=1}^m \alpha_{k, j} \bm{\theta}_j + \bm{\delta}_k, \\ \bm{l}_k = \exp(\sum_{j=1}^m \alpha_{k, j} \log (\bm{\lambda}_j) + \bm{\delta}_k'), \]

    则更一般的高阶信息可以用如下方式表示:

    \[\Delta_{ex} = \bm{l}_k e^{i \bm{\psi}_k}. \]

  • 得到 \(\Delta_{ex}\) 之后, 为了下一层的继续进行, 我们需要拆解出实部和虚部:

    \[\hat{\bm{r}}_k = \bm{l}_k \cos(\bm{\psi}_k), \\ \hat{\bm{p}}_k = \bm{l}_k \sin(\bm{\psi}_k). \\ \]

  • 如果有更多的高阶信息需要建模, 可以:

    \[\Delta_{ex} = \sum_{k=1}^n (\hat{\bm{r}}_k + i \hat{\bm{p}}_k). \]

Implict

  • 此外, Eulernet 还有 implict 的信息建模部分:

    \[\bm{r}_k' = \text{ReLU}(\mathbf{W}_k \bm{r} + \bm{b}_k), \\ \bm{p}_k' = \text{ReLU}(\mathbf{W}_k \bm{p} + \bm{b}_k). \\ \]

  • 两部分信息, 相加并通过 normlization layer 归一化.

优化

  • 假设最后的输出为:

    \[\{\tilde{\bm{r}}_k + i \tilde{\bm{p}}_k\}_{k=1}^n, \]

    通过如下方式进行回归预测:

    \[\hat{y} = \sigma(z_{re} + z_{im}), \\ z = \mathbf{w}^T \tilde{\bm{r}} + i (\mathbf{w}^T \tilde{\bm{p}}) = z_{re} + iz_{im}, \\ \tilde{\bm{r}} = [\tilde{\bm{r}}_1, \tilde{\bm{r}}_2, \ldots, \tilde{\bm{r}}_n] \in \mathbb{R}^{nd} \\ \tilde{\bm{p}} = [\tilde{\bm{p}}_1, \tilde{\bm{p}}_2, \ldots, \tilde{\bm{p}}_n] \in \mathbb{R}^{nd}. \\ \]

  • 然后通过 BCE 进行优化.

代码

[official]