ECC加密
之前机缘巧合研究过一段时间ECC的加密原理(指意义不明的手写笔记),刚好看到有ECC相关的题目就试试。
基础知识
较快地了解ECC算法:↓
https://blog.csdn.net/sitebus/article/details/82835492
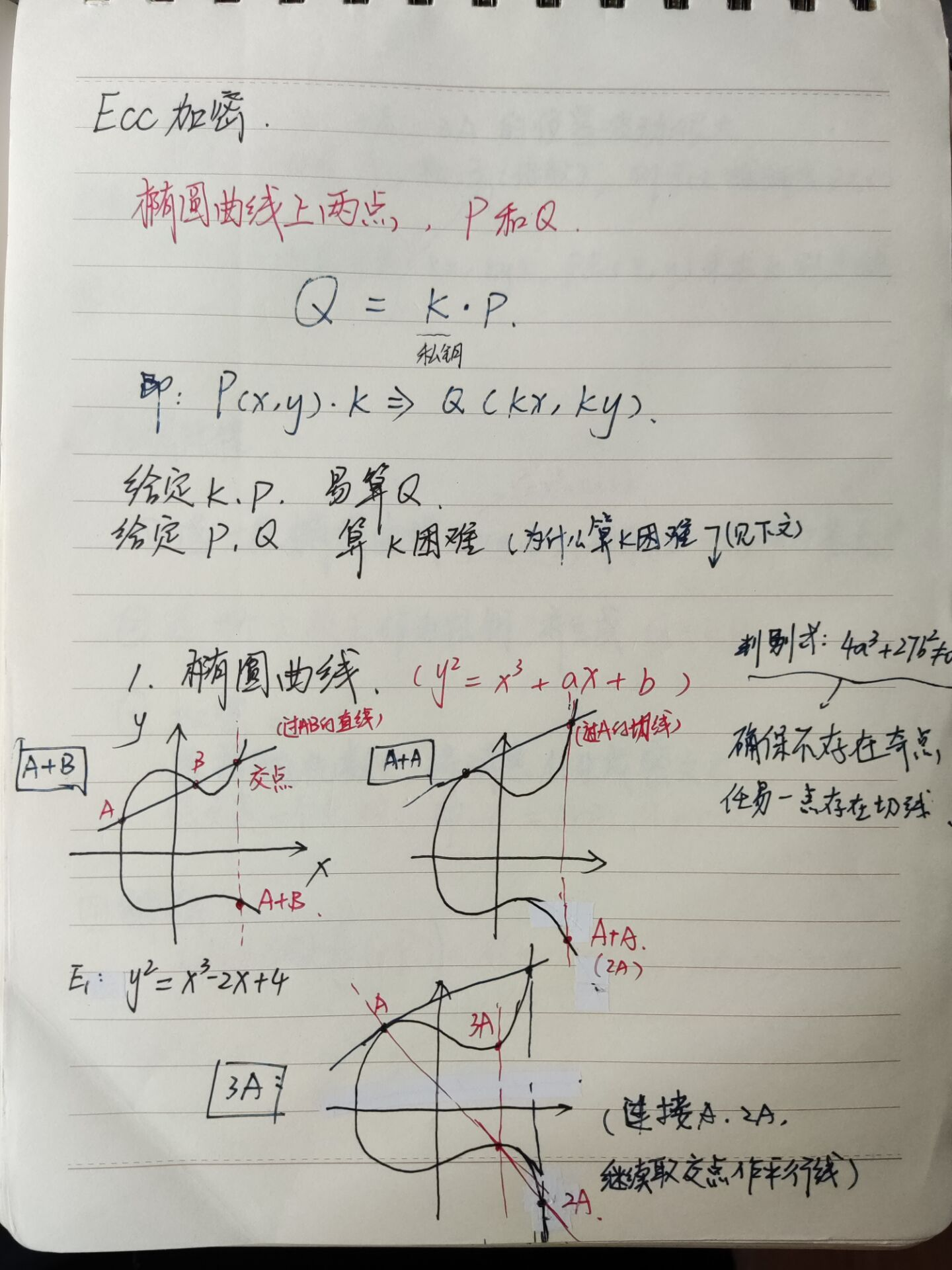

加密过程
1、用户A选定一条椭圆曲线Ep(a,b),并取椭圆曲线上一点,作为基点G。
2、用户A选择一个私有密钥k,并生成公开密钥K=kG。
3、用户A将Ep(a,b)和点K,G传给用户B。
4、用户B接到信息后 ,将待传输的明文编码到Ep(a,b)上一点M(编码方法很多,这里不作讨论),并产生一个随机整数r(r<n)
5、用户B计算点\(C 1 = M + r K和C_2 = rG\)
6、用户B将\(C_1、C_2\)传递给用户A
7、用户A接受到信息之后,计算\(C_1-kC_2\),这个所得的结果就是点M。
举例
1、Alice选定一条椭圆曲线E,并取椭圆曲线上一点作为基点G 假设选定E29(4,20),基点G(13,23) , 基点G的阶数n=37
2、Alice选择一个私有密钥k(k<n)比如25,并生成公开密钥K=kG = 25G = (14,6)
3、Alice将E和点K、G传给Bob
4、Bob收到信息后,将待传输的明文编码到E上的一点M,并产生一个随机整数r(r<n,n为G的阶数) 假设r=6 要加密的信息为3,因为M也要在E29(4,20) 上,所以M=(3,28)
5、Bob计算点\(C_1和C_2\)
\(C_1=M+rK=M+6K=M+6G=(3,28)+6×(14,6)=(3,28)+(27,27)=(6,12)\)
\(C_2=rG=6G=(5,7)\)
6、Bob将\(C_1、C_2\) 传给Alice
7、Alice收到信息后,计算\(C_1-kC_2\) ,结果就是:
$ M = C_1-kC_2 =(6,12)-25C_2=(6,12)-25\times(5,7) =(6,12)-(27,27) =(6,12)+(27,2) =(3,28)$
要求
通常将Fp上的一条椭圆曲线描述为T=(p,a,b,G,n,h)
p、a、b确定一条椭圆曲线(p为质数,用于(mod p)运算)G为基点,n为点G的阶,h是椭圆曲线上所有点的个数m与n相除的商的整数部分。
参量选择要求:
-
p越大安全性越好,但会导致计算速度变慢
-
200bit左右可满足一般安全要求
-
n应为质数 h≤4;p≠n×h ;pt≠1(mod n) (1≤t<20)
-
$ 4a^3 + 27b^2 \neq 0 \pmod p$(椭圆曲线判别式,确保不存在奇点,使任意一点均存在切点)
[watevrCTF 2019]ECC-RSA
题目
from fastecdsa.curve import P521 as Curve
from fastecdsa.point import Point
from Crypto.Util.number import bytes_to_long, isPrime
from os import urandom
from random import getrandbits
def gen_rsa_primes(G): #用于生成RSA的p和q
urand = bytes_to_long(urandom(521//8))
while True:
s = getrandbits(521) ^ urand #将得到的两个随机数再进行异或(估计是为了提升随机性)
Q = s*G #由此看来,这个s就是上文我们提到的椭圆加密的那个关键K值
if isPrime(Q.x) and isPrime(Q.y):
print("ECC Private key:", hex(s))
print("RSA primes:", hex(Q.x), hex(Q.y))
print("Modulo:", hex(Q.x * Q.y))
return (Q.x, Q.y)
flag = int.from_bytes(input(), byteorder="big")
ecc_p = Curve.p
a = Curve.a
b = Curve.b
Gx = Curve.gx
Gy = Curve.gy
G = Point(Gx, Gy, curve=Curve)
e = 0x10001
p, q = gen_rsa_primes(G)
n = p*q
file_out = open("downloads/ecc-rsa.txt", "w")
file_out.write("ECC Curve Prime: " + hex(ecc_p) + "\n")
file_out.write("Curve a: " + hex(a) + "\n")
file_out.write("Curve b: " + hex(b) + "\n")
file_out.write("Gx: " + hex(Gx) + "\n")
file_out.write("Gy: " + hex(Gy) + "\n")
file_out.write("e: " + hex(e) + "\n")
file_out.write("p * q: " + hex(n) + "\n")
c = pow(flag, e, n)
file_out.write("ciphertext: " + hex(c) + "\n")
ECC Curve Prime: 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
Curve a: -0x3
Curve b: 0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
Gx: 0xc6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66
Gy: 0x11839296a789a3bc0045c8a5fb42c7d1bd998f54449579b446817afbd17273e662c97ee72995ef42640c550b9013fad0761353c7086a272c24088be94769fd16650
e: 0x10001
p * q: 0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
ciphertext: 0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e
分析
首先我们可以看到题目定义了一个gen_rsa_primes函数,用于获取rsa的pq这俩大质数。
可以看到最后的flag其实是解RSA解出来的,主要问题就集中于如何解开椭圆曲线加密得出pq。
得到pq之后就是常规的解RSA了。
Q = s*G
G在这题里是基点,Q的横纵坐标就是我们所需要的pq。
因为使用的是椭圆曲线加密,即满足:\(y^2=x^3+ax+b\)
使用我们可以得到式子1:\(q^2=p^3+ap+b\) 其中a和b都是已知参数。
已知数据中还给了式子2:
p*q=0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
两个未知数两个式子,应该可以求解了。
将两个式子化简成一个:
即:
写sage脚本:
a=-0x3
b=0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
ECC_p=0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
n=0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
R.<x>=Zmod(ECC_p)[]
f=x**5+a*x**3+b*x**2-n**2
f.roots()
运行:
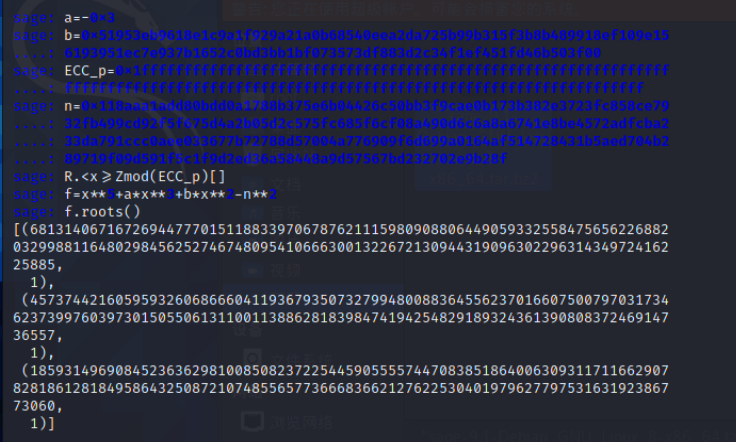
[(6813140671672694477701511883397067876211159809088064490593325584756562268820329988116480298456252746748095410666300132267213094431909630229631434972416225885,
1),
(4573744216059593260686660411936793507327994800883645562370166075007970317346237399760397301505506131100113886281839847419425482918932436139080837246914736557,
1),
(1859314969084523636298100850823722544590555574470838518640063093117116629078281861281849586432508721074855657736668366212762253040197962779753163192386773060,
1)]
可以看到有三个解,最后一个一看就知道不是质数,第一个其实也不是质数,不是质数则说明不是我们要的p的值。
只有第二个解是质数:
from Crypto.Util.number import long_to_bytes
import gmpy2
p=4573744216059593260686660411936793507327994800883645562370166075007970317346237399760397301505506131100113886281839847419425482918932436139080837246914736557
n=0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
q=n//p
phi=(p-1)*(q-1)
e=0x10001
d=gmpy2.invert(e,phi)
c=0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e
m=pow(c,d,n)
print(long_to_bytes(m))
得到flag:
b'watevr{factoring_polynomials_over_finite_fields_is_too_ez}'