有不少介绍扩散模型的资料,其中"Understanding Diffusion Models: A Unified Perspective"论文是我读到的解释最详细也是最易于理解的一个。
数学符号
- 用粗体字母表示向量, 如\(
\mathbf{x}, \mathbf{z}\)
- 用字母\(\mathbf{x}\)表示可观测到变量,用字母\(\mathbf{z}\)表示隐变量
- 用\(q_{\phi}(z|x)\)表示从观测变量\(x\)到隐变量\(z\)编码模型,模型参数用\(\phi\)表示,这个参数即可以是训练得到的也可以是人为设定的
证据下界 ELBO
假设观测到的变量\(x\)和其对应的隐变量\(z\)的联合概率分布用\(p(x,z)\)表示。回想有一种生成模型方法,称之为“基于似然”,该方法通过最大化观测的变量\(x\)的似然来构建模型。有两种方法来从联合概率分布\(p(x,z)\)得到仅仅是关于观测变量\(x\)的似然。
\[p(x) = \int p(x,z)dz \tag{1}
\]
\[p(x) = \frac{p(x,z)}{p(z|x)} \tag{2}
\]
从上述两个公式出发直接计算和最大化似然\(p(x)\)都是很困难的。因为公式(1)中对于复杂的模型,关于隐变量\(z\)求积分/边际分布是很困难的;公式(2)中求解真实的隐变量编码器\(p(z|x)\)也是很困难的。但是使用这两个公式可以推导出Evidence Lower Bound (ELBO)证据下界。这里的证据,是指观测到数据\(x\)的似然值对数\(\mathrm{log}\ p(x)\)。下面来推导证据下界公式
推导一
\[\begin{aligned}
\mathrm{log}\ p(x) &= \mathrm{log} \int p(x,z)dz \\
&= \mathrm{log} \int \frac{p(x,z)q_{\phi}(z|x)}{q_{\phi}(z|x)} dz \\
&= \mathrm{log}\ \mathbb{E}_{q_{\phi}(z|x)} \frac{p(x,z)}{q_{\phi}(z|x)} \\
&\geq \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)} \\
\end{aligned}
\tag{3}
\]
其中,用\(q_{\phi}(z|x)\)表示从观测变量\(x\)到隐变量\(z\)编码模型,模型参数用\(\phi\)表示,该编码模型学习估计一个概率分布,来近似在给定观测变量\(x\)下隐变量\(z\)的真实后验概率分布\(p(z|x)\)。公式首先利用公式(1)以及分子分母同时乘以\(q_{\phi}(z|x)\),将积分转化为期望。最重要的是利用Jensen不等式,交换期望与对数运算。
推导二
\[\begin{aligned}
\mathrm{log}\ p(x) &= \mathrm{log}\ p(x) \int q_{\phi}(z|x)dz \\
&= \int \mathrm{log}\ p(x) q_{\phi}(z|x)dz \\
&= \int \mathrm{log}\ \frac{p(x,z)}{p(z|x)} q_{\phi}(z|x)dz \\
&= \int \mathrm{log}\ \frac{p(x,z)q_{\phi}(z|x)}{p(z|x)q_{\phi}(z|x)} q_{\phi}(z|x)dz \\
&= \int [\mathrm{log}\ \frac{p(x,z)}{q_{\phi}(z|x)} + \mathrm{log}\ \frac{q_{\phi}(z|x)}{p(z|x)}] q_{\phi}(z|x)dz \\
&= \int \mathrm{log}\ \frac{p(x,z)}{q_{\phi}(z|x)}q_{\phi}(z|x) dz + \int \mathrm{log}\ \frac{q_{\phi}(z|x)}{p(z|x)}q_{\phi}(z|x) dz \\
&= \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)} + D_{KL}(q_{\phi}(z|x) || p(z|x)) \\
&\geq \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)} \\
\end{aligned}
\tag{4}
\]
推导二中,关键的一点是利用条件概率\(q_{\phi}(z|x)\)的积分等于1,然后再使用公式(2)替换概率\(p(x)\),再分子分母同乘以\(q_{\phi}(z|x)\),拆分得到KL散度项\(D_{KL}(q_{\phi}(z|x) || p(z|x))\)和\(\mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)}\)。
- 上述公式中,\(D_{KL}(q_{\phi}(z|x) || p(z|x))\),表示近似的后验概率分布\(q_{\phi}(z|x)\)与真实的后验概率分布\(p(z|x)\)之间的KL散度
- 上述公式中,\(\mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)}\),可以从形式看出,如果\(q_{\phi}(z|x)\)是真实的后验概率分布\(p(z|x)\),那么就刚好等于\(\mathrm{log}\ p(x)\),如果不等于那么\(\mathrm{log}\ p(x)\)就大于关于任意条件概率\(q_{\phi}(z|x)\)的$ \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)}$的期望。称 \(\mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)}\)为证据下界。
总结,证据=证据下界+近似后验与真实后验间的KL散度
为什么最大化ELBO可以代替最大化 \(\mathrm{log}\ p(x)\)
- 由于证据和ELBO之间就相差一个KL散度,KL散度本身是非负的,因此ELBO是证据的下界
- 引入想要建模的隐变量\(z\),目标就是学习能够描述观测的数据的根本隐藏的内在结构。换句话说,就是优化近似后验概率\(q_{\phi}(z|x)\)的参数,以达到精确匹配真实的后验概率\(p(z|x)\)。而这种匹配关系恰好通过最小化KL散度来实现。理想情况下KL散度值为0. 不幸的是,由于无法获取真实的后验概率分布\(p(z|x)\),因此是很难直接最小化KL散度。 但是注意到推导二中,观测到数据的似然对数即证据关于参数\(\phi\)是一个常量,因为它是通过对联合概率分布\(p(x,z)\)关于所有隐变量\(z\)求边际分布而不依赖参数\(\phi\)。因此,此处最小化KL散度等价于最大化ELBO,因此最大化ELBO,可以用来指导如何完美建模真实后验概率分布。此外,一旦训练完成,ELBO就可以用来估计观测到的或者生成数据的似然,因为它已经可以近似模型证据\(\mathrm{log}\ p(x)\).
变分自编码器 VAE
在变分自编码器VAE任务中,是直接最大化证据下界ELBO。之所以用“变分”修饰,是由于求解的结果是一个的函数而非一个值。
传统的AE模型,先是经过中间瓶颈表示步骤,将输入数据转化为与之对应的隐变量取值(encoder),然后再逆变换将隐变量取值转化为原始输入(decoder)。这里的AE模型特点是,输入数据与隐变量取值是一一对应的,并未设计成,给定一个输入数据\(x\),而与之对应的隐变量取值服从某个分布\(p(z|x)\)。因此AE模型无法截取decoder部分从中取样用于生成近似训练集分布的数据。
而变分自编码VAE中,encoder部分是将输入数据转化为与之对应所有可能隐变量取值,不同取值都具有不同的概率值。这样encoder部分输入是向量\(x\),输出是概率分布\(p(z|x)\),是一个函数。接下来decoder部分,学习一个确定性的函数\(p_{\theta}(x|z)\),给定隐变量取值,得到观察值\(x\)。
下面对ELBO进行进一步的拆解
\[\begin{aligned}
\mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p(x,z)}{q_{\phi}(z|x)}
&= \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} \frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)} \\
&= \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} [p_{\theta}(x|z)] + \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} [\frac{p(z)}{q_{\phi}(z|x)}] \\
&= \mathbb{E}_{q_{\phi}(z|x)} \mathrm{log} [p_{\theta}(x|z)] - \mathbb{D}_{KL}(q_{\phi}(z|x)||p(z))] \\
\end{aligned}
\tag{5}
\]
- 拆解的第1项表示,从encoder变分分布\(q_{\phi}(z|x)\)中取样,经过decoder合成部分\(p_{\theta}(x|z)\)重建出\(x\)的可能性。这一项保证了,学习到有效的概率分布,使得从中取样的隐变量取值能重建回对应的原始数据。
- 拆解的第2项表示,学习的变分分布与先验分布的相似性。最小化该项,则是鼓励encoder实际上是学习一个分布而不是退化为Dirac\(\delta\)函数。如果这样,就有点变成传统AE模型的意思了~
分级变分自编码器 HVAE
HVAE可以看成是VAE的一种扩展,将VAE由单个隐变量扩展到多个分级的隐变量。假设HVAE有\(T\)级/层隐变量,每个隐变量都可以条件依赖之前的所有隐变量,为了简化模型复杂度和便于计算,我们仅考虑条件依赖相邻之前的一个隐变量,称之为马尔科夫HVAE(MHVAE)。如图所示,在MHVAE中,encoder过程中,隐变量\(z_t\)仅条件依赖\(z_{t-1}\);在decoder过程中,隐变量\(z_t\)仅条件依赖\(z_{t+1}\)。接下来按照公式(1)和(2)推导MHVAE的ELBO,因此要先写出联合概率分布和后验概率分布的公式。
- 从decoder过程推导联合概率分布,看图上方由右到左容易得到
\[\begin{aligned}
p(x,z_{1:T})
&=p(x|z_1)p(z_1|z_2) \cdots p(z_{T-1}|z_T) p(z_T)\\
&=p(x|z_1)p(z_T)\prod_{t=1}^{T-1}p(z_t|z_{t+1})
\end{aligned}
\tag{6}
\]
- 从encoder过程推导联合概率分布,看图下方由左到右容易得到
\[\begin{aligned}
p(x,z_{1:T})
&=q(x)q(z_1|x)q(z_2|z_1) \cdots p(z_T|z_{T-1})\\
&=q(x)q(z_1|x)\prod_{t=1}^{T-1}q(z_{t+1}|z_t)
\end{aligned}
\tag{7}
\]
- 从encoder过程推导后验概率分布,看图容易得到
\[\begin{aligned}
q(z_{1:T}|x)
&= q(z_1|x)q(z_2|z_1) \cdots p(z_T|z_{T-1})\\
&= q(z_1|x)\prod_{t=1}^{T-1}q(z_{t+1}|z_t)
\end{aligned}
\tag{8}
\]
上面是理论推导,而encoder和decoder都用某种方式进行建模,encoder部分建模参数用\(\phi\)表示,decoder建模参数用\(\theta\)表示。于是,MHVAE的联合概率分布和后验概率分布可以表示为
\[\begin{aligned}
p(x,z_{1:T})
&=p_{\theta}(x|z_1)p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_{T-1}|z_T) p(z_T)\\
&=p(z_T)p_{\theta}(x|z_1)\prod_{t=1}^{T-1}p_{\theta}(z_t|z_{t+1})
\end{aligned}
\tag{9}
\]
\[\begin{aligned}
q_{\phi}(z_{1:T}|x)
&= q_{\phi}(z_1|x)q_{\phi}(z_2|z_1) \cdots p_{\phi}(z_T|z_{T-1})\\
&= q_{\phi}(z_1|x)\prod_{t=1}^{T-1}q_{\phi}(z_{t+1}|z_t)
\end{aligned}
\tag{10}
\]
直接应用公式(3),使用\(z_{1:T}\)替换其中的\(z\),便可以得到
\[\mathrm{log}\ p(x) \geq \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p(x,z_{1:T})}{q_{\phi}(z_{1:T}|x)} \tag{11}
\]
\[\mathrm{log}\ p(x) \geq \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p(z_T)p_{\theta}(x|z_1)\prod_{t=1}^{T-1}p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_1|x)\prod_{t=1}^{T-1}q_{\phi}(z_{t+1}|z_t)}
\tag{12}
\]
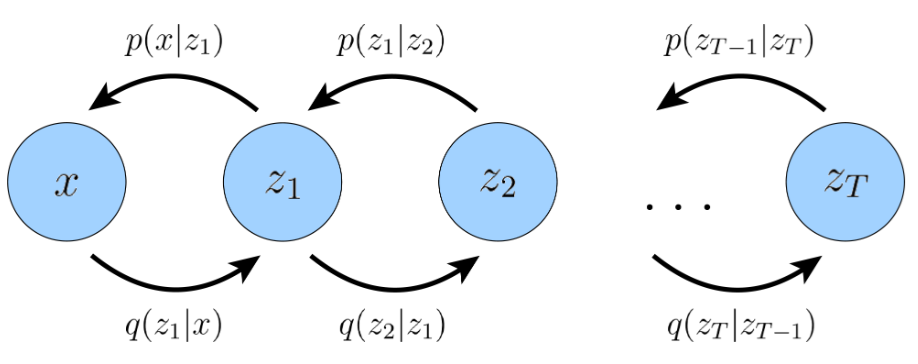
注: 为什么这么繁琐分两次推导这个公式呢?因为第一次是理论推导,概率分布符号表示也是采用一般的形式。而第二次引入参数符号\(\phi,\theta\)下标,一方面是为了区分;另一方面,为了后续便于计算,对要求解的条件概率进行某种形式的建模(比如假设是一种高斯分布),建模后条件概率就可以用参数\(\phi,\theta\)表达出来。不同的建模方式也有不同的参数化表达形式。
变分扩散模型 VDM
VDM可以看成是MHVAE的一种,相比MHVAE具有下面3个特点:
- 隐变量的维度与原始数据维度保持一致
- encocder过程,每个时间步的条件概率分布不是训练学习到的,而是预先设定的高斯分布
- 从初始数据出发,\(T\)个时间步后,得到数据服从高斯分布
基于上述公式,继续对ELBO进行拆解,还是习惯于去掉\(\prod\)符号,展开写更清晰些
\[\begin{aligned}
\mathrm{log}\ p(x)
&\geq \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p(z_T)p_{\theta}(x|z_1)\prod_{t=1}^{T-1}p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_1|x)\prod_{t=1}^{T-1}q_{\phi}(z_{t+1}|z_t)} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p(z_T)p_{\theta}(x|z_1) p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|x)q_{\phi}(z_2|z_1) \cdots q_{\phi}(z_{t+1}|z_t) \cdots p_{\phi}(z_T|z_{T-1})} \\
\end{aligned}
\tag{13}
\]
参考VAE中的拆解方式,需要将重建项和先验匹配项拆解出来,就对应此处的\(\mathrm{log}\ p_{\theta}(x|z_1)\)和\(\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}\),于是对上述公式进行改写
\[\begin{aligned}
\mathrm{log}\ p(x)
&\geq \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p(z_T)p_{\theta}(x|z_1)\prod_{t=1}^{T-1}p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_1|x)\prod_{t=1}^{T-1}q_{\phi}(z_{t+1}|z_t)} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p(z_T)p_{\theta}(x|z_1) p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|x)q_{\phi}(z_2|z_1) \cdots q_{\phi}(z_{t+1}|z_t) \cdots p_{\phi}(z_T|z_{T-1})} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|x)} [\mathrm{log}\ p_{\theta}(x|z_1)] + \mathbb{E}_{q_{\phi}(z_{1:T}|x)} [\frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}] + \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|x)q_{\phi}(z_2|z_1) \cdots q_{\phi}(z_{t+1}|z_t) \cdots p_{\phi}(z_{T-1}|z_{T-2})} \\
\end{aligned}
\tag{14}
\]
现在继续对上述公式最后一项进行进一步拆解,结合下图理解,粉色线和绿色线从两个不同方向对隐变量\(z_t\)进行条件概率分布建模
\[\begin{aligned}
& \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|x)q_{\phi}(z_2|z_1) \cdots q_{\phi}(z_{t+1}|z_t) \cdots p_{\phi}(z_{T-1}|z_{T-2})} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p_{\theta}(z_1|z_2)}{q_{\phi}(z_1|x)} + \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p_{\theta}(z_2|z_3)}{q_{\phi}(z_2|z_1)} + \cdots + \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})} + \cdots + \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \mathrm{log} \frac{p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_{T-1}|z_{T-2})}\\
\end{aligned}
\tag{15}
\]
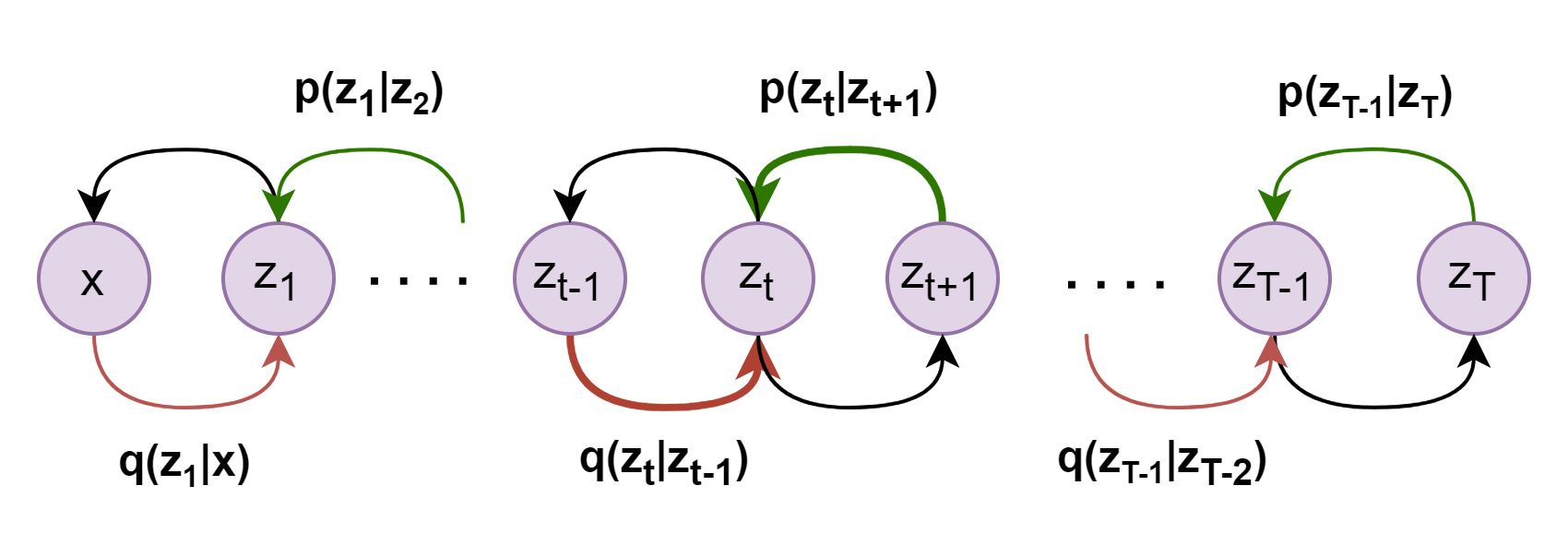
现在回到VDM的假设,初始数据\(x\)与隐变量\(z_t\)具有相同的维度,再加之后续公式表达的便捷,于是设置\(z_0=x\),而隐变量\(z_t\)其中\(t\in[1,T]\)。于是VDM的ELBO可以写成为如下形式:
\[\begin{aligned}
ELBO_{VDM}
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1)] \\
& +\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}] \\
& +\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p_{\theta}(z_1|z_2)}{q_{\phi}(z_1|z_0)} \\
& + \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p_{\theta}(z_2|z_3)}{q_{\phi}(z_2|z_1)} \\
& + \cdots \\
& + \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})} \\
& + \cdots \\
& + \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p_{\theta}(z_{T-1}|z_{T})}{q_{\phi}(z_{T-1}|z_{T-2})} \\
\end{aligned}
\tag{16}
\]
简化形式
\[\begin{aligned}
ELBO_{VDM}
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1)] \\
& +\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}] \\
& + \sum_{t=1}^{T-1} \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})}]
\end{aligned}
\tag{17}
\]
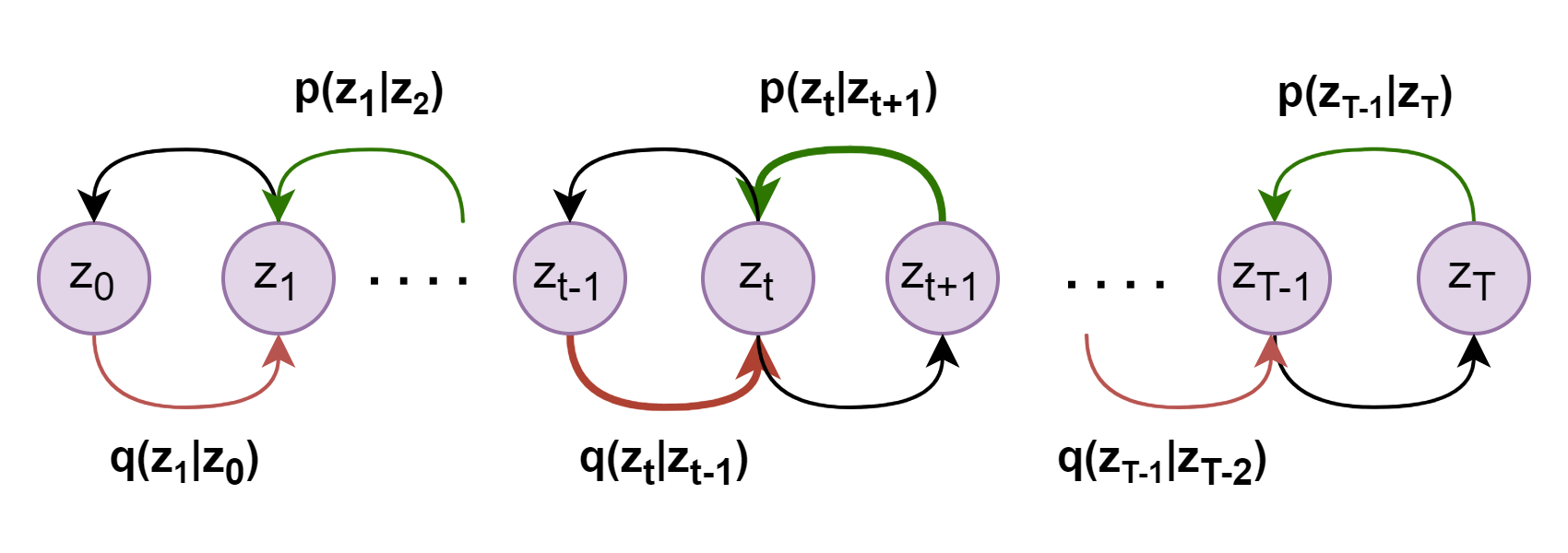
再回顾关于VDM对encoder部分每个时间步的高斯分布假设,设
\[z_t = \alpha_t z_{t-1} + \beta_t \epsilon_t
\]
其中,
\[\epsilon_t \sim \mathcal N(0, I)
\]
\[\alpha_t^2 + \beta_t^2 = 1, \alpha_t,\beta_t > 0
\]
然后可以推导出
\[z_t = \underbrace{(\alpha_t\cdots\alpha_1)}_{记为\bar{\alpha}_t} z_0 + \underbrace{\sqrt{1-(\alpha_t\cdots\alpha_1)^2}}_{记为\bar{\beta}_t} \bf{\bar \epsilon_t}, \bar \epsilon_t \sim \mathcal N(0, I)
\]
因此\(z_t\)服从高斯分布\(\mathcal N(\bar{\alpha}_t z_0, \bar{\beta}_t^2I)\),即\(q_{\phi}(z_t|z_{t-1})=q(z_t|\bar{\alpha}_t z_0, \bar{\beta}_t^2I)\)。
\[\begin{aligned}
q_{\phi}(z_{1:T}|z_0)
&=q_{\phi}(z_1|z_0)q_{\phi}(z_2|z_1) \cdots q_{\phi}(z_{t+1}|z_t) \cdots p_{\phi}(z_{T-1}|z_{T-2}) \\
&=q(z_1|\bar{\alpha}_1 z_0, \bar{\beta}_1^2I) q(z_2|\bar{\alpha}_2 z_0, \bar{\beta}_2^2I) \cdots q(z_t|\bar{\alpha}_T z_0, \bar{\beta}_T^2I) \\
\end{aligned}
\]
后面中每一项条件概率仅与\(z_0,z_t\)有关系的概率,因此上述公式中,与求期望内部项无关的变量可以消掉(转化为积分形式乘法项无关可以分离,概率的积分又等于1)。
因此,
\[\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1)] = \mathbb{E}_{q_{\phi}(z_1|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1)]
\]
\[\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}] = \mathbb{E}_{q_{\phi}(z_{T-1}, z_T|z_0)} [\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}]
\]
\[\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})}] = \mathbb{E}_{q_{\phi}(z_{t-1},z_t, z_{t+1}|z_0)} [\mathrm{log}\ \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})}]
\]
又由于\(q_{\phi}(z_{T-1}, z_T|z_0)=q_{\phi}(z_{T-1}|z_0)q_{\phi}(z_T|z_{T-1})\), 因此
\[\begin{aligned}
\mathbb{E}_{q_{\phi}(z_{T-1}, z_T|z_0)} [\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}]
&= \mathbb{E}_{q_{\phi}(z_{T-1}|z_0)} [q_{\phi}(z_T|z_{T-1})\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_{T-1})}] \\
&= -\mathbb{E}_{q_{\phi}(z_{T-1}|z_0)} [\mathbb{D}_{KL}(q_{\phi}(z_T|z_{T-1})||p(z_T))]
\end{aligned}
\]
又由于\(q_{\phi}(z_{t-1}, z_t, z_{t+1}|z_0)=q_{\phi}(z_{t-1},z_{t+1}|z_0)q_{\phi}(z_t|z_{t-1})\), 因此
\[\begin{aligned}
\mathbb{E}_{q_{\phi}(z_{t-1}, z_t, z_{t+1}|z_0)} [\mathrm{log}\ \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})}]
&= \mathbb{E}_{q_{\phi}(z_{t-1}, z_{t+1}|z_0)} [q_{\phi}(z_t|z_{t-1})\mathrm{log}\ \frac{p_{\theta}(z_t|z_{t+1})}{q_{\phi}(z_t|z_{t-1})}] \\
&= -\mathbb{E}_{q_{\phi}(z_{t-1}, z_{t+1}|z_0)} \mathbb{D}_{KL} (q_{\phi}(z_t|z_{t-1}) || p_{\theta}(z_t|z_{t+1})) \\
\end{aligned}
\]
最终得到VDM的变分下界
\[\begin{aligned}
ELBO_{VDM}
&= \mathbb{E}_{q_{\phi}(z_1|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1)] \\
& -\mathbb{E}_{q_{\phi}(z_{T-1}|z_0)} \mathbb{D}_{KL} (q_{\phi}(z_T|z_{T-1}) || p(z_T)) \\
& -\sum_{t=1}^{T-1} \mathbb{E}_{q_{\phi}(z_{t-1}, z_{t+1}|z_0)} \mathbb{D}_{KL} (q_{\phi}(z_t|z_{t-1}) || p_{\theta}(z_t|z_{t+1}))
\end{aligned}
\]
VDM变分下界各个子项解释
- \(\mathbb{E}_{q_{\phi}(z_1|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1)]\) 看作重建项,表示在给定第1步隐变量取值后,重建/得到原始数据的对数概率。
- \(\mathbb{E}_{q_{\phi}(z_{T-1}|z_0)} \mathbb{D}_{KL} (q_{\phi}(z_T|z_{T-1}) || p(z_T))\) 看作先验匹配项,表示最后一步的隐变量的分布与高斯先验分布之间的KL散度,最小化即要求这两个分布要相等或者匹配。由于隐变量的概率分布的特殊设计,这一点是可以保证的,不需要训练。
- \(\mathbb{E}_{q_{\phi}(z_{t-1}, z_{t+1}|z_0)} \mathbb{D}_{KL} (q_{\phi}(z_t|z_{t-1}) || p_{\theta}(z_t|z_{t+1}))\) 看作一致性项,表示对于每一个隐变量\(z_t\),从encoder方向编码出隐变量\(z_t\)概率分布与从decoder方向解码出\(z_t\)概率分布是相等的/一致的。
VDM优化主要集中在一致性项上面,因为是关于时间步进行求和共计T-1项。VDM的变分下界ELBO都是期望,因此可以使用蒙特卡罗估计方法进行近似计算。然而基于这些项进行求解优化并不是最优的,因为一致性项求期望是关于两个随机变量\(z_{t-1}, z_{t+1}\)进行计算的,使用蒙特卡罗估计的方差比基于单个随机变量的方差要大。而且\(T-1\)个一致性项加在一起,最终的方差可能更大。
因此就需要想办法减少期望中的随机变量的个数,此处的关键是将encoder过程中每个时间步变换\(q(z_t|z_{t-1})\)改写为\(q(z_t|z_{t-1},z_0)\)。这是因为马尔科夫特性仅条件依赖相邻的前一项,因此\(q(z_t|z_{t-1},z_0)\)中\(z_0\)添加上或者省略都不影响这个变换。因此
\[q(z_t|z_{t-1})=q(z_t|z_{t-1},z_0)
\]
在由贝叶斯公式改写每个时间步变换得到
\[q(z_t|z_{t-1},z_0) = \frac{q(z_{t-1}|z_t,z_0)q(z_t|z_0)}{q(z_{t-1}|z_0)}
\]
之所以如此变换,就是为了反转条件概率中变量的顺序,不再像上述推导中从encoder和decoder两个不同方向去保证时间步\(t\)时刻的隐变量\(z_t\)的条件概率分布一致,也就不会出现了期望是关于两个隐变量\(z_{t-1},z_{t+!}\)。如此变换后,从encoder和decoder部分得到的隐变量\(z_t\)的条件概率分布都条件依赖\(z_{t+1}\),从而实现了求期望过程中减少了随机变量的个数,从理论上减少了求解过程中的方差。
基于此,再对ELBO进行推导
\[\begin{aligned}
\mathrm{log}\ p(x)
&\geq \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p(z_T)\prod_{t=0}^{T-1}p_{\theta}(z_t|z_{t+1})}{\prod_{t=0}^{T-1}q_{\phi}(z_{t+1}|z_t)} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p(z_T)p_{\theta}(z_0|z_1) p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|z_0)q_{\phi}(z_2|z_1) \cdots q_{\phi}(z_{t+1}|z_t) \cdots p_{\phi}(z_T|z_{T-1})} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p(z_T)p_{\theta}(z_0|z_1) p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|z_0)q_{\phi}(z_2|z_1,z_0) q_{\phi}(z_3|z_2,z_0)\cdots q_{\phi}(z_{t}|z_{t-1},z_0) q_{\phi}(z_{t+1}|z_t,z_0) \cdots p_{\phi}(z_T|z_{T-1},z_0)} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p(z_T)p_{\theta}(z_0|z_1) p_{\theta}(z_1|z_2) p_{\theta}(z_2|z_3) \cdots p_{\theta}(z_{t-1}|z_t) p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_1|z_0) \frac{q_{\phi}(z_1|z_2,z_0)q_{\phi}(z_2|z_0)}{q_{\phi}(z_1|z_0)} \frac{q_{\phi}(z_2|z_3,z_0)q_{\phi}(z_3|z_0)}{q_{\phi}(z_2|z_0)} \cdots \frac{q(z_{t-2}|z_{t-1},z_0)q(z_{t-1}|z_0)}{q(z_{t-2}|z_0)} \frac{q(z_{t-1}|z_t,z_0)q(z_t|z_0)}{q(z_{t-1}|z_0)} \cdots \frac{p_{\phi}(z_{T-1}|z_{T},z_0)q_{\phi}(z_T|z_0)}{q_{\phi}(z_T|z_0)}} \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} \mathrm{log} \frac{p(z_T)p_{\theta}(z_0|z_1) p_{\theta}(z_1|z_2) \cdots p_{\theta}(z_t|z_{t+1}) \cdots p_{\theta}(z_{T-1}|z_T)}{q_{\phi}(z_{1}|z_2,z_0)q_{\phi}(z_{2}|z_3,z_0) \cdots q_{\phi}(z_{t-2}|z_{t-1},z_0) q_{\phi}(z_{t-1}|z_t,z_0) \cdots q_{\phi}(z_{T-1}|z_T,z_0) q_{\phi}(z_T|z_0) } \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1) + \mathrm{log} \ \frac{p(z_T)}{q_{\phi}(z_T|z_0)} + \sum_{t=2}^{T}\mathrm{log}\ \frac{p_{\theta}(z_{t-1}|z_t)}{q_{\phi}(z_{t-1}|z_t,z_0)} ] \\
&= \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1) ]+ \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log} \ \frac{p(z_T)}{q_{\phi}(z_T|z_0)}] + \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\sum_{t=2}^{T}\mathrm{log}\ \frac{p_{\theta}(z_{t-1}|z_t)}{q_{\phi}(z_{t-1}|z_t,z_0)} ] \\
&= \mathbb{E}_{q_{\phi}(z_{1}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1) ]+ \mathbb{E}_{q_{\phi}(z_{T}|z_0)} [\mathrm{log} \ \frac{p(z_T)}{q_{\phi}(z_T|z_0)}] +\sum_{t=2}^{T} \mathbb{E}_{q_{\phi}(z_{t-1},z_t|z_0)} [\mathrm{log}\ \frac{p_{\theta}(z_{t-1}|z_t)}{q_{\phi}(z_{t-1}|z_t,z_0)} ] \\
\end{aligned}
\]
\[\begin{aligned}
ELBO_{VDM}
&=\mathbb{E}_{q_{\phi}(z_{1:T}|z_0)}[\mathrm{log}\ p_{\theta}(z_0|z_1) ]+ \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\mathrm{log}\ \frac{p(z_T)}{q_{\phi}(z_T|z_0)}] + \mathbb{E}_{q_{\phi}(z_{1:T}|z_0)} [\sum_{t=2}^{T}\mathrm{log}\ \frac{p_{\theta}(z_{t-1}|z_t)}{q_{\phi}(z_{t-1}|z_t,z_0)}] \\
&= \mathbb{E}_{q_{\phi}(z_{1}|z_0)} [\mathrm{log}\ p_{\theta}(z_0|z_1) ]+ \mathbb{E}_{q_{\phi}(z_{T}|z_0)} [\mathrm{log} \ \frac{p(z_T)}{q_{\phi}(z_T|z_0)}] +\sum_{t=2}^{T} \mathbb{E}_{q_{\phi}(z_{t-1},z_t|z_0)} [\mathrm{log}\ \frac{p_{\theta}(z_{t-1}|z_t)}{q_{\phi}(z_{t-1}|z_t,z_0)} ] \\
\end{aligned}
\]


