A Randomized Algorithm for Single-Source Shortest Path on Undirected Real-Weighted Graphs

Ran Duan , Jiayi Mao , Xinkai Shu , and Longhui Yin

这篇翻译必定有相当多的错漏，仅起到抛砖引玉的作用，各位大佬们有兴趣可以看原论文

7.11发表于arxiv的原论文

前排膜拜大佬先

单源最短路算法的革新！

从 Abstract 来看，时间复杂度是 \(O(m\sqrt{\log n \cdot \log \log n})\)

主要面向问题为：在一张非负实数边权无向图上，给定一个起点 \(S\)，问从 \(S\) 到每个点的最短长度为多少。这被称为单源最短路问题。

翻译人为：andychen_2012(3.2节之前), Nostalgia(3.3节-第4节), wiki0922(第5节)

1、简介

问题简介与历史略去。

1.1 我们的成果

在本文中，我们提出了第一个无向实加权图的SSSP算法，该算法打破了排序瓶颈。

算法1 在一张非零实数边权无向图 \(G=(V,E,w)\) 中，每条边都有一个边权 \(w:E \to \mathbb R_{\ge 0}\)。有一种基于比较加法的 Las-Vegas 随机化算法，能够在 \(O(m\sqrt{\log n\cdot \log\log n})\) 的时间复杂度内解决单源最短路问题，其结果总是正确的，并且有很高的概率能够抵达这个时间复杂度。这个时间复杂度可以在 \(m=\omega(n)\) 且 \(m=o(n\log n)\) 的情况下被优化到 \(O(\sqrt{mn\log n}+n\sqrt{\log n\log \log n})\)。

注意到对于无向实加权SSSP的“基于层次(hierarchy-based)”算法，有一个最坏的时间复杂度 \(\Omega(m+\min\{n\log n,n\log \log r \})\)，但我们的算法是随机的，而不是基于层次的，因此不受这个时间复杂度的约束。讨论情况见备注 Remark 2。

技术概述 基于 Dijkstra 的算法的瓶颈是优先级队列。因此，我们只将一小部分顶点添加到优先队列中。正如在许多关于距离预言机（Distance oracle）或 spanners（指图 \(G\) 中的子图，保留了原图的最短路长度，但有一定程度的失真，失真程度不超过某个数值，通常来说是可加和/或可乘的）的工作中一样，我们对点的进行采样，得到一个仅包含点的子集 \(R\)，并且堆也仅包含 \(R\) 中的点，然后我们将每一个其他顶点 \(v\) “捆绑”到其在 \(R\) 中最近的点，称为 \(b(v)\)。然后将 \(\operatorname{Ball}(v)\) 定义为比 \(b(v)\) 更接近 \(v\) 的点集。由于该算法不知道最短路径上大多数点的正确顺序，因此像 Dijkstra 的算法那样只对邻点进行松弛操作是不起作用的。（Dijkstra 的松弛操作指：假设当前起点和终点分别为 \(u,v\)，遍历一遍起点 \(u\) 的邻点，设当前遍历到点 \(t\)，观察以 \(t\) 作为中转站会不会能够使得 \(u,v\) 间的距离更短，如果更近了就更新距离）

因此，当从堆中弹出一个点 \(u \in R\) 时，我们也处理与 \(u\) 捆绑的点 \(v\)。在无向图中，这也意味着 \(| \operatorname{dist}(s,u) - \operatorname{dist}(s,v) |\) 不大。在这里，我们从 \(\operatorname{Ball}(v)\) 中选取点及其邻点，用这些点来松弛 \(v\)，使得我们能够更新 \(v\) 的邻点到 \(Ball(v)\) 中的点的最短距离。（为了更容易描述，我们首先将图更改为具有 \(O(m)\) 个顶点的常度数图）算法的细节以及正确性和运行时间的分析将在第 3 节中讨论。第4节将介绍 bundles（也即上文提到的捆绑）的详细构造，以便算法能够保证高概率的正确率，并且在规定的时间复杂度运行完成。第5节将讨论通过放松 constant-degree 约束来提高时间复杂性。

1.2 其他人近期的工作

2、前置知识与约定

在这篇论文里，我们在无向图 \(G=(V,E,w)\) 上进行讨论，其中 \(V\) 为 \(G\) 的点集，边集 \(E \subseteq V^2\)，并且有非负实数函数 \(w:E \to \R_{\ge 0}\)，由该边的连接的两个点 \(u,v\) 决定，也可以被表示为 \(w_{uv}\)。在一张无向图中，\(w_{uv}=w_{vu}\) 对所有边 \((u,v) \in E\) 都满足。我们约定 \(n=|V|,m=|E|\)，分别表示图的点数与边数。我们还约定 \(N(u)=\{v:(u,v) \in E \}\)，表示 \(u\) 的所有邻点。对于两个点 \(u,v \in V\)，\(\operatorname{dist}_G(u,v)\) 表示 \(u\) 到 \(v\) 的最短路径长度，被称为 \(u\) 到 \(v\) 的距离。当不至于引起歧义时，我们省略下标 \(G\)。我们设 \(s\) 为源点。我们这个算法的目标是对于所有的 \(v \in V\) 计算出 \(\operatorname{dist}(s,v)\)。在不失一般性的情况下，我们假设 \(G\) 是连通的，因此 \(m\ge n−1\)。

Constant-Degree Graph. 在整篇论文中，我们需要一张常度数图（constant-degree graph）。为了实现这个目的，给出一张图 \(G\)，我们通过一个经典的转换来构造 \(G'\):

用一个与零权边相连的 \(|N(v)|\) 点集 \(x_{vw}(w\in N(v))\) 的环替换每个点 \(v\) ，也就是说，对于 \(v\) 的每个邻点 \(w\)，在这个环上都有一个点 \(x_{vw}\) 对应。
对于在 \(G\) 中的每条边 \((u,v)\)，在相应的点 \(x_{uv}\) 和 \(x_{vu}\) 上连接一条无向边，权值为 \(w_{uv}\)。

我们可以观察到 \(\operatorname{dist}_{G'}(x_{uu'},x_{vv'})=\operatorname{dist}_G(u,v)\)，这对于任意的 \(u' \in N(u)\) 且 \(v' \in N(v)\) 都是成立的。对于每个在 \(G'\) 中的点，它的度数顶多为 3，而 \(G'\) 则是一个有 \(O(m)\) 个点和 \(O(m)\) 条边的图。

Comparison-Addition Model. 在这篇论文中，我们的算法在比较加法模型(comparison-addition model) 下运作，其中实数只进行比较和加法运算。在这个模型中，每次加法和比较操作都花费一个单位时间，并且对于边权的其他运算是不被允许的。

**Fibonacci Heap. ** 在这个模型下，我们可以构造一个 Fibonacci Heap \(H\)，用于初始化、插入、减少操作的时间复杂度均摊后为 \(O(1)\)，以及用于将最小值取出的操作的时间复杂度均摊后为 \(O(\log |H|)\)。当我们将堆中的最小值取出时，我们也称这个元素被从堆中弹出。

3、主要算法

在下面的小节中，我们假定 \(G\) 是连通的，并且 \(G\) 中的每个点有不超过 \(3\) 的度数（有 \(O(m)\) 个点和 \(O(m)\) 条边在 \(G\) 中，但我们依旧认为 \(O(\log n)=O(\log m)\) 的等价关系成立，这里的 \(n\) 指的是原图中没有最大度数限制时点的个数）

我们的算法基于最原始的 Dijkstra 的算法。由于 Dijkstra 的算法的瓶颈在于每次从 Fibonacci Heap 中取出最小值都需要花费 \(O(\log n)\) 的时间复杂度，因此我们只把子点集 \(R \subseteq V\) 加入到堆中。所有剩下的点 \(v \in V \backslash R\) 都被 bundled(捆绑) 到了 \(R\) 中离它最近的点。在整个算法中，点集只会在某些点 \(u \in R\) 被弹出堆时被更新。我们的算法包含两个部分：bundle construction 和 Bundle Dijkstra，在 3.1 节和 3.2 节中将分别介绍它们。

为了演示我们算法的主要思想，在这一章中，我们给出一个预期时间复杂度为 \(O(m\sqrt{\log n \cdot \log \log n})\) 的算法，但是不能够保证高概率达到这个时间复杂度。在第 4 章中，我们将给出一个 bundle construction stage 的进阶版本，能够使得整个算法很高概率做到 \(O(m\sqrt{\log n \cdot \log \log n})\) 的时间复杂度。不过两种算法都能够正确地给出答案。

3.1 Bundle Construction

我们给出 Bundle Construction 的一个简单版本，运行步骤如下（\(k\) 是稍后确定的参数）：

独立地选取每个点 \(v \in V \backslash \{s \}\)，每个 \(v\) 都有 \(\frac{1}{k}\) 的概率被选到。被选出的 \(v\) 组成点集 \(R\)，然后再把 \(s\) 加入到 \(R\) 中。
对于每个点 \(v \notin R\)，从 \(v\) 开始跑一边 Dijkstra，直到 \(R\) 的第一个点被从堆中取出。这个点被标记为 \(b(v)\)。因此 \(b(v)\) 是 \(R\) 中到 \(v\) 的最近的点，也就是说 \(b(v) \in \arg \min_{u\in R} \operatorname{dist}(u,v)\)。我们称 \(v\) 与 \(b(v)\) 捆绑。（\(\arg \min\) 表示的是使得后面式子取最小值的变量的取值）
对于每个 \(u \in R\)，我们让 \(b(u)=u\)，并且 \(\operatorname{Bundle}(u)=\{v:u=b(v) \}\) 被定义为被捆绑到 \(u\) 上的点集。根据定义 \(\{\operatorname{Bundle}(u) \}_{u\in R}\) 构成了点集 \(V\) 的一个划分。
对于每个点 \(v \notin R\)，定义 \(\operatorname{Ball}(v)=\{w\in V:\operatorname{dist}(v,w)<\operatorname{dist}(v,b(v)) \}\)，也就是说，比 \(b(v)\) 到 \(v\) 的距离更近的点组成的点集。在先前的 Dijkstra 算法中，我们可以得到 \(\operatorname{Ball}(v)\) 并且对于所有 \(w \in \operatorname{Ball}(v) \cup \{b(v) \}\) 可以得到 \(\operatorname{dist}(v,w)\) 的值。

Time Analysis of Bundle Construction. 对于每个 \(v \notin R\)，不失一般性地，我们假定它的 Dijkstra 算法以确定性的方式打破了平衡。因此，从堆中提取的点的顺序是固定的。

我们可以观察到 \(\Bbb{E}[|R|]=O(m/k)\)。对于每个点 \(v \notin R\)，让 \(S_v\) 表示在它的 Dijstra 算法停止前，被提取的点组成的点集，那么 \(\operatorname{Ball}(v) \subsetneq S_v\)。根据 \(R\) 的定义，\(|S_v|\) 满足成功概率为 \(\frac{1}{k}\) 的几何分布，因此 \(\Bbb{E}[|S_v|]=k\) 且 \(\Bbb{E}[|\operatorname{Ball}(v)|] \le k\)。根据最大度数性质，被加入堆中的点数也是 \(O(|S_v|)\)。因此 bundle construction 的总的期望时间复杂度为 \(\large O(\sum\limits_{v\in V\backslash R} \Bbb{E}[|S_v|\log |S_v|])=O(mk\log k)\)。

Remark 1. 有的人可能注意到 \(x\log x\) 是一个凸函数，因此 \(\Bbb{E}[|S_v|\log |S_v|]=O(k\log k)\) 的成立不是很明显。我们现在给出一个简单的证明（通过几何分布 \(\Bbb{E}[|S_v|^2]=2k^2-k\)：

\[\begin{aligned} \Bbb{|S_v|\log |S_v|}&= \sum_{n=1}^{\infty} \frac{1}{k}(1-\frac{1}{k})^{n-1} \cdot n\log n\\ &\le \sum_{n\le k^2}\frac{1}{k}(1-\frac{1}{k})^{n-1} \cdot n\log n +\sum_{n>k^2}\frac{1}{k}(1-\frac{1}{k})^{n-1}\cdot n^2\\ &\le 2\log k\sum_{n \le k^2}\frac{1}{k}(1-\frac{1}{k})^{n-1}\cdot n+\sum_{n=1}^{\infty} \frac{1}{k}(1-\frac{1}{k})^{k^2+(n-1)}(n+k^2)^2\\ &\le 2\log k \cdot \Bbb{E}[|S_v|]+(1-\frac{1}{k})^{k^2}\cdot \Bbb{E}[(|S_v|+k^2)^2]\\ &\le 2k\log k + e^{-k} \cdot O(k^4)\\ &=O(k\log k) \end{aligned} \nonumber \]

3.2 Bundle Dijkstra

给定集合 \(R\) 和 bundles 的划分，主要算法的运行原理如下，伪代码在算法中给出：

一开始我们设 \(d(s)=0\) 且对于所有其他点 \(v\) 设 \(d(v)=+\infty\)。然后将 \(R\) 中的所有点插入到一个 Fibonacci heap 中。每当我们将一个点 \(u \in R\) 从堆中弹出，我们就通过如下不中更新距离（这里的用值 \(D\) 松弛一个点 \(v\) 表示我们将 \(d(v)\) 更新为 \(\min\{d(v),D \}\)）

对于每个被捆绑到 \(u\) 上的 \(v\)，我们需要找到 \(\operatorname{dist}(s,v)\) 的确切值。我们首先用 \(d(u)+\operatorname{dist}(u,v)\) 松弛点 \(v\)。然后对于每个点 \(y \in \operatorname{Ball}(v)\)，用 \(d(y)+\operatorname{dist}(y,v)\) 松弛点 \(v\)。并且对于每个 \(z_2 \in \operatorname{Ball}(v) \cup \{v \}\) 与 \(z_1 \in N(z_2)\)，用 \(d(z_1) +w_{z_1,z_2}+\operatorname{dist}(z_2,v)\) 松弛点 \(v\)。也就是说，我们通过捆绑点 \(u\)，\(\operatorname{Ball}(v)\) 中的点集，与 \(v\) 与 \(\operatorname{Ball}(v)\) 相邻的点集来更新 \(d(v)\)。
在对所有 \(x \in \operatorname{Bundle}(u)\) 更新完 \(d(x)\) 后，我们更新 \(y \in N(x)\) 和 \(z_1 \in \operatorname{Ball}(y)\)。也就是说，对所有 \(y \in N(x)\)，用 \(d(x)+w_{x,y}\) 松弛点 \(y\)，然后对所有 \(z_1 \in \operatorname{Ball}(y)\)，用 \(d(x)+w_{x,y}+\operatorname{dist}(y,z_1)\) 松弛点 \(z_1\)。
每当我们更新完一个点 \(v \notin R\)，我们也将其捆绑点 \(b(v)\) 用 \(d(b)+\operatorname{dist}(v,b(v))\) 松弛。（但稍后我们将看到，这仅在步骤2中需要，而在步骤1中不需要，因为在步骤1中将 \(v\) 绑定到 \(u\)，但在从堆中弹出 \(u\) 时已经找到距离 \(\operatorname{dist}(s,u)\)。）

下面的观察可以从算法中自然地得出

Observation 2. \(d(v) \ge \operatorname{dist}(s,v)\) 对于所有

Time Analysis for Bundle Dijkstra. 对于 Bundle Dijkstra 这一过程，只有 \(R\) 中的点会被插入到堆中，因此取出最小值的操作总共只花费 \(O(|R|\log n)\) 的时间复杂度。因为每个在 \(V \backslash R\) 中的点只被当作 \(v\) 和 \(x\) 在步骤1和步骤2中各出现了一次，并且通过最大常数度数性质，每个点只被当作 \(y \in N(x)\) 在步骤2出现了常数次，因此步骤1中对于每个 \(v\) 的点 \(z_1,z_2\) 的个数是 \(O(|\operatorname{Ball}(v)|)\) 个，并且对于步骤1和步骤2中，每个点 \(y\) 所对应的点 \(z_1,z_2\) 的个数为 \(O(|\operatorname{Ball}(y)|)\) 个。同时我们注意到步骤3中Relax的递归调用只能递归一次，因为 \(b(v) \in R\)。所以步骤1，2，3的总时间复杂度为 \(O(\sum_{v \in V \backslash R}|\operatorname{Ball}(v)|)\)。因此，Bundle Dijkstra 过程的时间复杂度为 \(\Bbb{E}[O(|R|\cdot \log n+\sum_{v \in V \backslash R}|\operatorname{Ball}(v)|)]=O(\frac{m}{k}\log n+mk\log k)\)，在 \(k=\sqrt{\frac{\log n}{\log \log n}}\) 时取得最小值 \(O(m\sqrt{\log n\cdot \log \log n})\)。我们来解释我们关于正确性证明的主要观点。第3.3节给出了正式证明。

Main ideas. 以下命题在算法中成立。（这里 \(u\) 的迭代意味着当弹出 \(u \in R\) 时执行的迭代；找到实距离 \(\operatorname{dist}(s,v)\) 意味着 \(d(v)= \operatorname{dist}(s,v)\) 已经成立。）

Proposition 3. 当 \(u \in R\) 从堆中弹出时，它的距离 \(\operatorname{dist}(s,u)\) 已经找到了。

Proposition 4. 在步骤1中，\(u\) 的迭代结束后，对于所有的 \(v \in \operatorname{Bundle}(u)\)，\(\operatorname{dist}(s,v)\) 都被找到了。

以下引理包含了该算法的主要思想。

Lemma 5. 对于任何点 \(u\in R\) 和任何从 \(s\) 到 \(u\) 的路径 \(P\)，如果 \(P\) 经过点 \(y\)，\(\operatorname{dist}(s,b(y))\) 至多是 \(P\) 的长度。

证明：\(\operatorname{dist}(s,y)\) 最多为 \(P\) 从 \(s\) 到 \(y\) 的子路径长度。根据 \(b(y)\) 的定义，\(\operatorname{dist}(y,b(y))\) 最多是 \(P\) 从 \(y\) 到 \(u\) 的子路径长度。将两条子路径连接在一起，\(\operatorname{dist}(s,b(y)) \le \operatorname{dist}(s,y)+\operatorname{dist}(y,b(y))\)，长度最大为 \(P\)。

引理5表明，对于任意点 \(u \in R\)，从 \(s\) 到 \(u\) 的最短路径只包含点 \(y\) 和 \(\operatorname{dist}(s,b(y)) \le \operatorname{dist}(s,u)\)。这就是为什么 \(R\) 的点按 \(\operatorname{dist}(s,\cdot)\) 的递增顺序弹出的原因。但是，从 \(s\) 到某个顶点 \(v \in \operatorname{Bundle}(u)\) 的最短路径可能会经过某个顶点 \(y\) 满足 \(\operatorname{dist}(s,b(y)) \ge \operatorname{dist}(s,u)\)，也就是说 \(b(y)\) 仍然不会从堆中弹出。但令人惊讶的是，使用引理6的想法，我们甚至可以在 \(b(y)\) 迭代之前处理这种情况。

Lemma 6. 对于一个点 \(v \notin R\)，如果从 \(s\) 到 \(v\) 的最短路径比 \(\operatorname{dist}(s,b(v))+\operatorname{dist}(b(v),v)\) 短，并且它经过一个点 \(y\) （不是 \(v\)），使得 \(\operatorname{dist}(s,b(y)) \ge \operatorname{dist}(s,b(v))\)，那么在从 \(y\) 到 \(v\) 的最短路径中，有两个相邻的顶点 \(z_1,z_2\)，使得 \(z_1 \in \operatorname{Ball}(y) \cup \{y \}\) 且 \(z_2 \in \operatorname{Ball}(v) \cup \{v \}\)。

证明：我们有 \(\operatorname{dist}(y,v) = \operatorname{dist}(s,v)-\operatorname{dist}(s,y)\) 和 \(\operatorname{dist}(s,v) < \operatorname{dist}(s,b(v))+\operatorname{dist}(b(v),v)\)。通过三角不等式 \(\operatorname{dist}(s,y) \ge \operatorname{dist}(s,b(y))-\operatorname{dist}(y,b(y))\) 和 \(\operatorname{dist}(s,b(y)) \ge \operatorname{dist}(s,b(v))\)，我们可以得到

\[\begin{aligned} \operatorname{dist}(y,v) &< \operatorname{dist}(b(v),v)+\operatorname{dist}(y,b(y))+\operatorname{dist}(s,b(v))-\operatorname{dist}(s,b(y))\\ &\le \operatorname{dist}(b(v),v)+\operatorname{dist}(y,b(y)) \end{aligned} \nonumber \]

设 \(z_1\) 是从 \(y\) 到 \(v\) 的最短路径上满足 \(\operatorname{dist}(y,z_1)<\operatorname{dist}(y,b(y))\) 的最后一个点，即 \(z_1 \in \operatorname{Ball}(y)\)。然后 \(z_2\) 是 \(z_1\) 连接的下一个点。所以 \(\operatorname{dist}(y,z_2) \ge \operatorname{dist}(y,b(y))\)，并且还有 \(\operatorname{dist}(z_2,v)<\operatorname{dist}(v,b(v))\)，因此 \(z_2 \in \operatorname{Ball}(v)\)。（如果 \(\operatorname{dist}(y,b(y))=0\)，那么 \(z_1=y\)，如果 \(\operatorname{dist}(y,v) <\operatorname{dist}(y,b(y))\)，那么 \(z_2=v\) 且 \(z_1\) 是 \(v\) 之前的那个点）

然后我们可以看到命题3和4在整个算法中可以迭代成立：（形式化证明将在3.3节给出）。

当我们从堆中弹出源 \(s\) 时，\(d(s)=0\) 和对于所有 \(v \in \operatorname{Bundle}(s)\) 的距离 \(\operatorname{dist}(s,v)\) 在 bundle construction 步骤中得到，并可以放在步骤1中的 \(d(v)\) 中。
假设命题4对首先弹出的 \(i\) 个点成立，那么就可以找到所有与弹出顶点捆绑在一起的点的实际距离。通过步骤2和3，我们可以看到对于所有未弹出的 \(u \in R\)，如果从 \(s\) 到 \(u\) 的最短路径没有经过那些被捆绑到堆中其他未弹出的点上的点，则可以找到距离 \(\operatorname{dist}(s,u)\)。如果下一个弹出的点 \(u'\) 不满足这一点，那么令 \(y\) 是从 \(s\) 到 \(u'\) 的最短路径上的第一个点，并且它被捆绑到一个未弹出的点 \(b(y)\)，而不是 \(u'\)，因此 \(\operatorname{dist}(s,b(y))\) 可以被找到。由引理5，我们可以得到 \(\operatorname{dist}(s,b(y)) \le \operatorname{dist}(s,u')\)，所以如果 \(d(u)>\operatorname{dist}(s,u')\)，那么 \(b(y)\) 将是下一个被弹出的点。因此，\(\operatorname{dist}(s,u')\) 对于下一个弹出的点 \(u'\) 而言，是在 \(u'\) 弹出之前找到的。
如果弹出的顶点 \(u\) 在迭代中更新了未弹出的点 \(u' \in R\)，则到 \(u'\) 的新路径必须经过 \(\operatorname{Bundle}(u)\) 中的点。根据引理5，\(d(u')\) 不能被更新为小于 \(\operatorname{dist}(s,u)\) 的数，因此未弹出的点必须比任何弹出的顶点具有更长或相等的（到 \(s\)）的距离。
因此当弹出一个点 \(u \in R\)，它的距离 \(\operatorname{dist}(s,u)\) 已经被找到了。对于所有满足 \(v \in \operatorname{Bundle}(s)\) 的点 \(v\)，如果 \(\operatorname{dist}(s,v)\) 不是直接从 \(d(u)+\operatorname{dist}(u,v)\) 得到的，也就是说，\(\operatorname{dist}(s,v)<\operatorname{dist}(s,u)+\operatorname{dist}(u,v)\)，那么我们令 \(x\) 是 \(s\) 到 \(v\) 的最短路径上的最后一个点满足 \(b(x)\) 在 \(u\) 之前被弹出，然后令 \(y\) 是 \(x\) 的下一个点。我们可以观察到 \(\operatorname{dist}(s,b(y)) \ge \operatorname{dist}(s,u)\)，所以根据引理6，我们可以得到 \(z_1\) 和 \(z_2\)。然后根据命题4，我们可以在步骤1 \(b(x)\) 的迭代中得到 \(\operatorname{dist}(s,x)\)，而在步骤2的迭代中，我们可以得到 \(\operatorname{dist}(s,z_1)\)。在 \(u\) 的这次迭代中，\(\operatorname{dist}(s,v)\) 可以在步骤1种被设置为 \(\operatorname{dist}(s,z_1)+w_{z_1,z_2}+\operatorname{dist}(z_2,v)\)，因此命题4在这次迭代后依旧成立。

3.3 正确性证明

基于前面算法 1 的伪代码，我们给出一个形式化的证明。令 \(u_i\in R\) 表示算法 1 中第 \(i\) 轮 while 循环中的顶点。我们在下面给出的引理展示了算法的主要特点，即无论 \(R\) 如何选取，bundle Dijkstra总是正确的

引理 7.

下面的性质对于在 bundle Dijkstra（算法 \(1\)）过程的任何 \(i\ge 1\) 成立

当 \(u_i\) 在堆中被弹出时，\(d(u_i)=\operatorname{dist}(s,u_i)\) 成立
在 while 循环中的第 \(i\) 次迭代后，\(d(u)\ge d(u_i)\) 对 \(\forall u\in R\backslash\{u_j\}_{j\le i}\) 成立
在 while 循环中的第 \(i\) 次迭代的步骤 \(1\) 被执行后，\(d(v)\ge \operatorname{dist}(s, v)\) 对 \(\forall v\in \operatorname{Bundle}(u_i)\) 成立

证明：我们将通过对 \(i\) 作归纳来证明引理

对于 \(i=1\) 的情况，该引理成立，因为 \(d(s)=0\)，且 \(d(v)=\operatorname{dist}(s,v)\) 对 \(\forall v\in\operatorname{Bundle}(s)\) 在算法第 \(7\) 行后成立

假设引理对于每个 \(i\le t-1\) 成立，考虑 \(i=t\) 时的情况

考虑一条从 \(s\) 到 \(u_t\) 的最短路径 \(P\)，令 \(x\) 为路径 \(P\) 上满足 \(\exists j<t,x\in \operatorname{Bundle}(u_j)\) 的最后一个节点，\(y\) 为 \(x\) 的下一个节点，因此 \(y\in \operatorname{Bundle}(u)\) 对一些满足 \(u\in R\backslash\{u_{\mathscr l}\}_{\mathscr l<t}\) 的 \(u\) 成立，通过归纳假设中的性质 \(3\)，\(d(x)=\operatorname{dis}(s, x)\) 在 \(j\) 次迭代的第一步后成立。因为 \(u\in N(x)\)，在那之后算法会更新 \(d(y)\)，接下来在第 \(15\) 行会更新 \(d(u)\)。

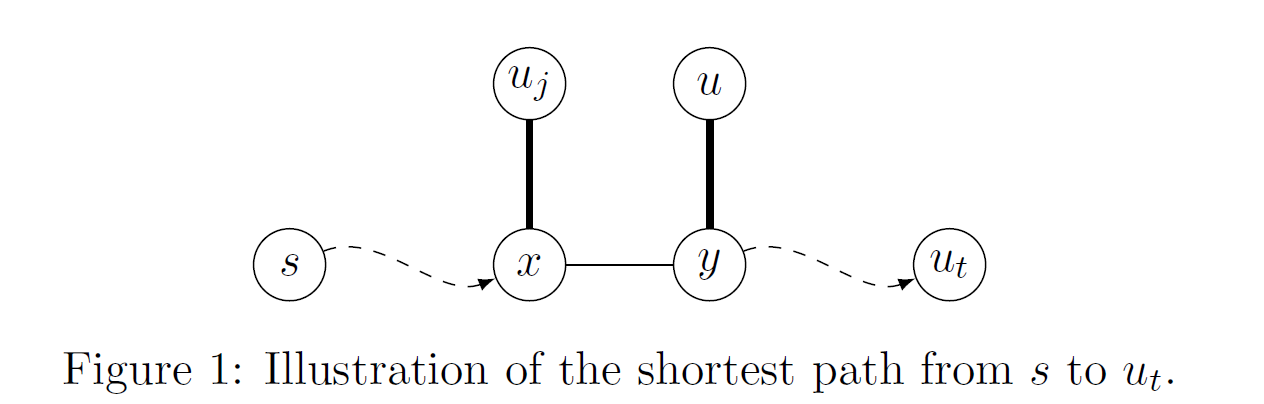
因此，在 \(t-1\) 轮迭代后，\(d(y)=\operatorname{dist}(s, x)+\operatorname{dist}(x,y)=\operatorname{dist}(s,y)\) 且 \(d(u)\le \operatorname{dist}(s,y)+\operatorname{dist}(y,u)\)

\[\begin{aligned} d(u)&\le \operatorname{dist}(s,y)+\operatorname{dist}(y,u)\\ &\le \operatorname{dist}(s,y)+\operatorname{dist}(y,u_t)&(\operatorname{b}(y)=u)\\ &=\operatorname{dist}(s,u_t)&(y在最短路径上)\\ &=d(u_t)&(观察2) \end{aligned} \nonumber \]
反过来说，当算法在 \(t-1\) 次迭代后立即从 Fibonacci 堆 \(H\) 中取出 \(u_t\)。所以所有的不等式变为等式，也就是说 \(d(u_t)=\operatorname{dist}(s,u_t)\)
由于 \(H\) 是一个 Fibonacci 堆，在执行完第 \(t\) 次迭代中伪代码的第 \(5\) 行时，\(d(u)\ge d(u_t)\) 对 \(\forall u\in R\{u_j\}_{j\le t}\) 成立。假设对某些 \(u\in R\backslash\{u_{\mathscr l}\}_{\mathscr l<t}\) 有 \(d(u)<d(u_t)\)，则接下来对 \(d(u)\) 的更新一定是从某些 \(x\in \operatorname{Bundle}(u_t)\)。对最后一次这样的更新中，从 \(s\) 到 \(x\) 再到 \(u\) 的路径应用引理 \(5\)，我们可以得到

\[\begin{aligned} d(u)&\ge \operatorname{dist}(s,u_t) &(引理5)\\ &=d(u_t) &(性质1) \end{aligned} \nonumber \]
从而矛盾
我们希望证明 \(d(v)=\operatorname{dist}(s,v)\) 对所有 \(v\in \operatorname{Bundle}(u_t)\) 成立。假设在步骤 \(1\) 后存在一个节点 \(v\in \operatorname{Bundle}(u_t)\) 有 \(d(v)>\operatorname{dist}(s,v)\)

记 \(P\) 为从 \(s\) 到 \(v\) 的最短路径。令 \(x\) 为 \(P\) 中满足 \(\exists j<t,x\in \operatorname{Bundle}(u_j)\) 的最后一个节点，\(y\) 为 \(x\) 在最短路径上的下一个节点，从而对于一些 \(u\in R\backslash \{u_{\mathscr l}\}_{\mathscr l<t}\) 有 \(y\in\operatorname{Bundle}(u)\)。通过归纳假设中的性质 \(3\)，在第 \(j\) 次迭代的步骤 \(1\) 后有 \(d(x)=\operatorname{dist}(s,x)\)。与上面同理，在第 \(t\) 次迭代前我们可以得到 \(d(y)=\operatorname{dist}(s,x)+\operatorname{dist}(x,y)=\operatorname{dist}(s,y)\)，并且 \(d(u)\le \operatorname{dist}(s, y)+\operatorname{dist}(y,u)\)（此处 \(u=\operatorname{b}(y)\)）。我们有：

\[\begin{aligned} \operatorname{dist}(s,y)&\ge d(u)-\operatorname{dist}(y,u).\\ \operatorname{dist}(s,v)&<d(v) &(假设)\\ &\le d(u_t)+\operatorname{dist}(u_t,v)&(d(v)在第\ 7\ 行更新了) \end{aligned} \nonumber \]
反过来说，通过性质 \(2\) 在 \(t\) 轮迭代后有 \(d(u)\ge d(u_t)\)。因为 \(d(u_t)\) 没有改变（性质 \(1\) 与观察 \(2\)），并且 \(d(u)\) 只有在第 \(t\) 轮迭代后才会减小，所以 \(d(u)\ge d(u_t)\) 在整个第 \(t\) 轮迭代中成立，从而：

\[\begin{equation} \operatorname{dist}(y,v)=\operatorname{dist}(s,v)-\operatorname{dist}(s,y)<\operatorname{dist}(u_t,v)+\operatorname{dist}(y,u) \end{equation} \]
当 \(y\) 在 \(s\) 到 \(v\) 的最短路上时等式成立

因此有两种可能的情况：
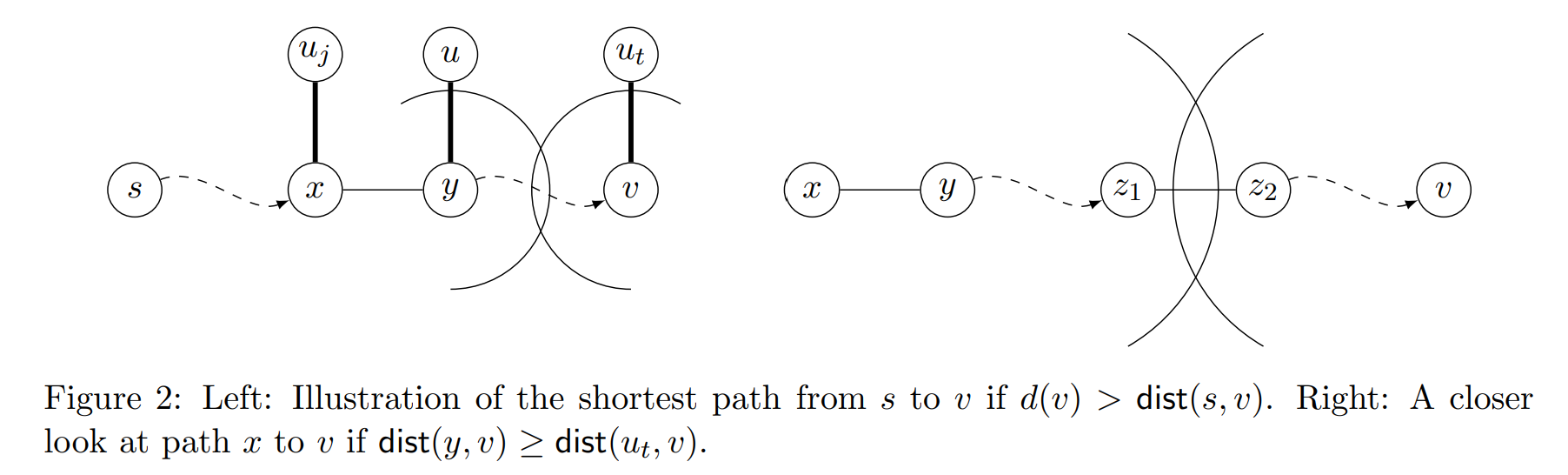
- \(\operatorname{dist}(y,v)<\operatorname{dist}(u_t,v)\)
  
  在这种情况下 \(y\in \operatorname{Ball}(v)\)，所以我们能在伪代码的第 \(9\) 行中将 \(d(v)\) 更新为 \(\operatorname{dist}(s,y)+\operatorname{dist}(y,v)\)，与 \(d(v)>\operatorname{dist}(s,v)\) 矛盾
- \(\operatorname{dist}(y,v)\ge \operatorname{dist}(u_t,v)\)
  
  首先通过不等式 \((1)\)，有 \(\operatorname{dist}(y,u)>\operatorname{dist}(y,v)-\operatorname{dist}(u_t,v)\ge 0\)。令 \(z_1\) 为路径 \(P\) 上满足 \(\operatorname{dist}(y,z_1)<\operatorname{dist}(y,u)\) 的最后一个节点，我们有 \(z_1\in \operatorname{Ball}(y)\)。令 \(z_2\) 表示路径上的下一个节点，那么 \(\operatorname{dist}(y,z_2)\ge \operatorname{dist}(y,u)\)，所以 \(\operatorname{dist}(z_2,v)=\operatorname{dist}(y,v)-\operatorname{dist}(y,z_2)\le \operatorname{dist}(y,v)-\operatorname{dist}(y,u)<\operatorname{dist}(u_t,v)\)，也就是说 \(z_2\in \operatorname{Ball}(v)\)（若 \(z_2\) 不存在，则 \(z_1=v\)）。通过归纳假设中的性质 \(3\)，就在 \(j\) 轮迭代的步骤 \(1\) 后 \(d(x)=\operatorname{dist}(s,x)\)，随后在第 \(j\) 轮迭代的第 \(17\) 行 \(d(z_1)\) 被更新为 \(\operatorname{dist}(s,z_1)\)。所以在第 \(t\) 轮迭代的第 \(12\) 行 \(d(v)\) 被更新为 \(\operatorname{dist}(s,v)\)（因为 \(j<t\)），与假设矛盾。
所以 \(d(v)=\operatorname{dist}(s,v)\) 在第 \(t\) 轮迭代后对所有 \(v\in\operatorname{Bundle}(u_t)\) 成立。

Q.E.D.

Remark2暂略

4、改进的 Bundle 构造

在这一节中我们将给出一个以高概率在 \(O(m\sqrt{\log n\cdot \log \log n})\) 的时间复杂度下运行的改进的 bundle 构造方法。在第 \(3.3\) 节我们展示了 bundle Dijkstra 的正确性并不依赖于 \(R\) 的选择，只要 \(\operatorname{b}(\cdot),\operatorname{Ball}(\cdot)\) 和 \(\operatorname{Bundle}(\cdot)\) 基于 \(R\) 被正确地计算出来。bundle 的构造时间复杂度为 \(O(\sum_{v\in V\backslash R}|S_v|\log |S_v|)\)，而 bundle Dijkstra 的时间复杂度为 \(O(\sum_{v\in V\backslash R}|\operatorname{Ball}(v)|+|R|\log n)\)

自然地，对于每个节点 \(v\in V\)，\(|S_v|\) 是一个服从几何分布的随机变量，但他们不是彼此独立的，因为一个节点 \(x\in V\) 可能在若干个集合中出现。但是对于一个子集 \(W\subset V\)，如果任何节点在 \(\{S_v\}v\in W\) 中出现最多一次，相应的随机变量 \(\{S_v\}_{v\in W}\) 是彼此独立的。通过引理 \(9\)，如果每个随机变量依赖于少数其他变量，它们的和以指数小的概率偏离期望。所以我们手动将所有满足 \(|S_v|\ge k\log k\) 的节点加入 \(R\) 中。这样对于所有 \(V\backslash R\) 中的节点，其随机变量仅依赖于有限的其他节点，所以我们可以以一个高的概率绑定他们的总和。

我们将在下面介绍如何生成 \(R\) 和计算 \(\{\operatorname{b}(v)\}_{v\in V\backslash R}\)，以及 \(\{\operatorname{Ball}(v)\}_{v\in V\backslash R},\{\operatorname{Bundle}(u)\}_{u\in R}\) 还有所有满足 \(u\in \operatorname{Ball}(u)\cup \{\operatorname b(u)\}\) 的 \(\operatorname{dist}(v, u)\)，伪代码将在算法 \(2\) 中给出。与第 \(3\) 节中同样，我们仍然设参数 \(k=\sqrt{\dfrac{\log n}{\log \log n}}\)

改进的Bundle构造

以 \(\frac{1}{k}\) 的概率对每个顶点 \(v\in V\backslash \{s\}\) 进行采样组成集合 \(R_1\)，再把 \(s\) 加入 \(R_1\) 中
对于每个 \(v\in V\backslash R_1\)，以 \(v\) 为源点进行 Dijkstra 算法，直到我们取出了一个 \(R_1\) 中的顶点；或者已经弹出了 \(k\log k\) 个节点
在前面的情况中，将弹出的节点按他们出现的顺序记录为列表 \(V^{(v)}_{extract}\)，注意 \(V^{(v)}_{extract}\) 与第 \(3\) 节中的 \(S_v\) 类似

在后面的一种情况，将 \(v\) 加入 \(R_2\)
令 \(R=R_1\cup R_2\)，对于所有 \(v\in V\backslash R\)，令 \(R\) 中在 \(V^{(v)}_{extract}\) 中的第一个节点为 \(\operatorname b(v)\)
根据上面的结果对 \(u\in R\) 的 \(u\) 计算 \(\operatorname{Bundle}(u)\)，对 \(v\in V\backslash R\) 的 \(v\) 计算 \(\operatorname {Ball}(v)\)，并记录对所有 \(u\in \operatorname{Ball}(v)\cup \{\operatorname b(u)\}\) \(\operatorname{dist}(v,u)\)，这一步仅需要线性时间。

这个 Bundle 的构造的正确性同 Dijkstra 算法。我们只需要分析 \(|R|,\sum_{v\in V\backslash R}|\operatorname{Ball}(v)|\) 以及其时间复杂度。这种改进的 bundle 的构造方法的特性见下面的引理 \(8\)。从引理 \(8\) 中，我们得到 bundle 的构造时间复杂度为 \(O(mk\log k)\)，并且 bundle Dijkstra 有 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率时间复杂度为 \(O(\sum_{v\in V\backslash R}|\operatorname{Ball}(v)|+|R|\log n)=O(mk\log n/k)\)，故在 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率下，我们算法总的运行时间为 \(O(mk\log k+m\log n/k)=O(m\sqrt{\log n\cdot \log \log n})\)。引理 \(8\) 的证明基于引理 \(9\)。

引理 8.

通过运行算法 \(2\)，有 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率，以下的性质成立

\(|R|=O(\frac{m}{k})\)。
\(\sum_{v\in V\backslash R}|\operatorname{Ball}(v)|=O(mk)\)
算法 \(2\) 运行的时间是 \(O(mk\log k)\)

证明

首先，对于每个 \(V\backslash \{s\}\) 中的节点都互不影响地以 \(\frac{1}{k}\) 的概率插入 \(R_1\)，所以根据 Chernoff 界，在 \(1-O(e^{-m/k})=1-e^{-\Omega(n^{1-o(1)})}\) 的概率下，\(|R_1|=\Theta(m/k)\)，并且同时 \(m':=|V\backslash R_1|=\Theta(m)\)，对于每个节点 \(v\in V\backslash R_1\)，定义 \(X_v=\mathbb I[v\in R_2]\) 和 \(Y_v=|V^{(v)}_{extract}|\)。则 \(X_v\) 为 Bernoulli 随机变量，\(X_v\in [0,1]\) 的概率为 \(1\)，并且 \(\mathbb E[X_v]=(1-\frac{1}{k})^{k\log k}=\Theta (\frac{1}{k})\)。而 \(Y_v\) 是一个几何随机变量，其值最多为 \(k\log k\)，\(Y_v\in [0, k\log k]\) 的概率为 \(1\)，并且 \(\mathbb E[Y_v]=k(1-(1-\frac{1}{k})^{k\log k})=\Theta (k)\)。

对于所有节点 \(v\in V\backslash R_1\)，记 \(V^{(v)}_{full}\) 为没有被中断的 Dijkstra 过程中的前 \(k\log k\) 个节点。它们由图 \(G\) 的结构决定，所以 \(V^{(v)}_{full}\) 中没有随机要素。\(X_v\) 与 \(Y_v\) 的值由 \(V^{(v)}_{full}\) 中的节点是否被插入 \(R_2\) 决定。因此，如果 \(V^{(v_1)}_{full},V^{(v_2)}_{full},\cdots, V^{(v_j)}_{full}\) 是无交的，则 \(X_{v_1},X_{v_2},\cdots, X_{v_j}\) 是相互独立的，类似地，\(Y_{v_1},Y_{v_2},\cdots, Y_{v_j}\) 也是相互独立的。

对每个节点 \(w\in V^{(v)}_{full}\)，因为 \(v\) 通过 Dijkstra 的 \(k\log k\) 步中找到了 \(w\)，必定存在一条不超过 \(k\log k\) 条边的从 \(v\) 到 \(w\) 的路径，所以根据常度数的性质，最多有 \(3\cdot (1+2+\cdots+2^{k\log k-1})\le 3\cdot 2^{k\log k}\) 个不同的 \(u\) 令 \(w\in V^{(u)}_{full}\)。从而，对每个 \(v\)，最多有 \(3k\log k\cdot2^{k\log k}=O(n^{o(1)})\) 个不同的 \(u\in V\backslash R_1\) 令 \(V^{(v)}_{full}\cap V^{u}_{full}\neq \empty\)，为了应用引理 \(9\)，对每个 \(v\in R_1\)，也像 \(v\) 在算法 \(2\) 中的循环中取出时那样定义 \(X_v, Y_v\) 以及 \(V^{(v)}_{full}\)。

现在，我们对 \(\{X_u\}_{u\in V}\) 和 \(\{Y_v\}_{v\in V}\) 应用引理 \(9\)。对 \(\{X_v\}_{v\in V}\)，\(S\) 即 \(V\)，并且 \(|V|=,\mu=\Theta(\frac{1}{k}),b=1,T=O(n^{o(1)})\)，并且 \(\{W_v\}_{v\in V}\) 是 \(\{V^{(v)}_{full}\}_{v\in V}\)，我们可以验证 \(8Tb\mu^{-1}=O(n^{o(1)})\) 和 \(8b^3T/\mu^3=O(n^{o(1)})\)，所以 \(\sum_{v\in S}X_v=\Theta(m/k)\) 至少有 \(1-e^{-\Omega(m/n^{o(1)})}\) 的概率成立。并且对于 \(\{Y_v\}_{v\in V}\)，\(S\) 为 \(V\)，\(\mu=\Theta(k)\)，\(b=k\log k\)，\(T=O(n^{o(1)})\)，并且 \(\{W_v\}_{v\in V}\) 同样为 \(\{V^{(v)}_{full}\}_{v\in V}\)，类似地我们可以推断，\(\sum_{v\in S}Y_v=\Theta(mk)\) 至少有 \(1-e^{-\Omega(m/n^{o(1)})}\) 的概率成立。因此我们得出结论，有 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率，\(\sum_{v\in S}X_v=\Theta(m/k)\) 且 \(\sum_{v\in S}Y_v=\Theta(mk)\)

随后，我们证明引理的三个部分

对 \(1\)，由定义可知 \(|R|=|R_1|+|R_2|\)，通过联合约束，有 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率 \(|R|=|R_1|+\sum_{v\in V\backslash R_1}X_v=O(\frac{m}{k})\)

对 \(2\)，由定义可知 \(|\operatorname{Ball}(v)|\le Y_v\)，所以 \(\sum_{v\in V\backslash R}|\operatorname{Ball}(v)|\le \sum_{v\in V\backslash R_{1}}Y_v\)。从而有 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率，\(\sum_{v\in V\backslash R}|\operatorname{Ball}(v)|=O(mk)\)。

对 \(3\)，我们对在所有迭代中被中断的 Dijkstra 算法进行计数，对每个节点 \(v\in V\backslash R_1\)，根据常度数的性质，\(\operatorname{INSERT}\) 操作的次数是 \(O(Y_v)\)，故 \(H^{(v)}=O(|Y_v|)=O(k\log k)\)，从而，每个 \(\operatorname{ExctractMin}\) 操作需要 \(O(\log (Y_v))=O(\log k)\) 的时间复杂度，并且其他操作仅需要常数时间。从而从 \(v\) 出发被中断的 Dijkstra 算法所需时间为 \(O(Y_v\log k)\)。从而，在 \(1-e^{-\Omega(n^{1-o(1)})}\) 的概率下，算法 \(2\) 的时间复杂度为 \(O(\sum_{v\in V\backslash R_1}Y_v\log k)=O(mk\log k)\)

Q.E.D.

引理 9.(类似参考文献 \(21\))

一个随机变量的集合 \(\{Z_v\}_{v\in S}\) 满足对于所有 \(v\in S,\mathbb E[Z_v]=\mu,Z_v\in [0,b]\) 有 \(1\) 的概率，并且每个 \(Z_v\) 对应一个确定性的集合 \(W_v\) 使得如果 \(W_{v_1},W_{v_2},\cdots,W_{v_j}\) 是无交的，则 \(Z_{v_1},Z_{v_2},\cdots ,Z_{v_j}\) 是相互独立的，并且 \(W_v\) 最多与 \(T\) 个不同的 \(W_u\) 有交。

\[那么，至少有1-8Tb\mu^{-1}\cdot e^{-\frac{\mu^3|S|}{8b^3T}} 的概率,有 \sum_{v\in S}Z_v=\Theta(|S|\mu) \nonumber \]

证明

我们尝试将 \(\{Z_v\}_{v\in S}\) 分为几个子集合 \(\{\mathcal Z_t\}\) 使得每个 \(\mathcal Z_t\) 中的所有 \(Z_v\) 都是相互独立的，从而我们可以使用 Hoeffding 不等式，或者 \(\mathcal Z_t\) 足够小使得我们可以通过上界 \(b\) 把他们结合起来，最后使用联合界将所有东西结合起来。请注意我们并不需要实际计算出 \(\{\mathcal Z_t\}\)，他们只是为了数学证明引入的。

固定参数 \(p=\frac{|S|\mu}{4Tb}\)，因为每个 \(W_v\) 最多与其他 \(T\) 个不同的 \(W_u\) 有交，无论如何至少有 \(p(T+1)\) 个元素在 \(\{Z_v\}_{v\in S}\) 中，我们可以从中选择 \(p\) 个不同的 \(Z_v\)，因为他们的 \(W_v\) 是无交的，所以他们是相互独立的：选择任意一个 \(Z_v\) 并丢弃那些使得 \(W_u\cap W_v\neq \emptyset\) 的 \(Z_u\)，因为最多有 \(T\) 个这样的 \(Z_u\) 不同于 \(Z_v\)，每次最多丢弃 \(T+1\) 个元素。所以我们可以从 \(p(T+1)\) 中个元素中选取 \(p\) 个。我们令他们组成一个 \(\mathcal Z_t\) 并在 \(\{Z_v\}_{v\in S}\) 中一处他们，重复这个过程，我们最终得到 \(\{Z_v\}_{v\in S}\) 的一个划分 \(\{\mathcal Z_1,\mathcal Z_2,\cdots, \mathcal Z_p, \mathcal Z_{p+1}\}\)

从而：\(\{\mathcal Z_t\}=p\)，并且对于所有满足 \(1\le t\le q;|\mathcal Z_{q+1}|\le p(T+1)\le 2pT=\frac{\mu}{2b}|S|\)的 \(Z_v\in \mathcal Z_t\) 都是相互独立的。由定义有 \(\mu\le b\)，所以 \(|\mathcal Z_{q+1}\le \frac{1}{2}|S|\)。

接下来根据 Hoeffding 不等式，对每个 \(1\le t\le q\)，

\[\operatorname{Pr}\bigg[\Bigg|\sum_{v\in\mathcal Z_t}Z_v-|\mathcal Z_t|\mu\Bigg|>\frac{1}{2}|\mathcal Z_t|\mu\bigg]\le 2e^{\frac{2(\frac{1}{2}|\mathcal Z_t|\mu)^2}{|Z_t|b^2}}=2e^{-\frac{\mu^2p}{2b^2}} \nonumber \]

并且 \(0\le \sum_{v\in\mathcal Z_{q+1}}Z_v\le |Z_{q+1}|b\) 的概率为 \(1\)

通过联合约束，至少有 \(1-2qe^{-\frac{\mu^2p}{2b^2}}\) 的概率

\[\sum_{v\in S}Z_v\ge \frac{1}{2}\sum_{t=1}^{q}|\mathcal Z_t|\mu=\frac{1}{2}(|S|-|\mathcal Z_{q+1}|)\mu\ge \frac{1}{2}\bigg(|S|-\frac{1}{2}|S|\bigg)\mu=\frac{1}{4}|S|\mu \nonumber \]

并且同时

\[\sum_{v\in S}Z_v\le \frac{3}{2}\sum_{t=1}^{q}|\mathcal Z_t|\mu+|\mathcal Z_{q+1}|b\le \frac{3}{2}|S|\mu+\frac{\mu}{2b}|S|\cdot b=2|S|\mu \nonumber \]

从 \(|S|\ge \sum_{t=1}^{q} |\mathcal Z_t|\ge pq\)，我们总结得到 \(q\le |S|/p=4Tb/\mu\)。从而，至少有 \(1-8Tb\mu^{-1}e^{-\frac{\mu^3|S|}{8b^3T}}\)，有 \(\sum_{v\in S}Z_v=\Theta(|S|\mu)\)

Q.E.D.

5、讨论

我们非常感谢一位匿名审稿人指出常数度不为该算法的必要条件，所以我们可以当 \(m = \omega(n)\) 或 \(m = o(n\log n)\) 时提升算法复杂度。不将图变成三度数图，我们用类似的方法将度数 \(> m/n\) 的结点分裂成度数 \(\le m/n\) 的若干结点，以保证结点的个数仍是 \(O(n)\) 的。

下面是步骤：

在 Bundle 的构造中，每个结点 \(v\) 的 Dijkstra 搜索时间将变为 \(O(|S_v|\cdot\frac m n + |S_v|\log(|S_v|\cdot \frac m n))\)，因为堆的大小至多为 \(|S_v|\cdot \frac m n\)，所以总共为 \(O(mk + nk\log(mk/n))\)。
Bundle Dijkstra 的时间将变为 \(O(\frac n k\log n+mk)\)，因为对于步骤一中的每个 \(v\)，\(z_2\) 的数量是 \(O(\frac m n|\mathsf{Ball}(v)|)\)；对于步骤二中的每个 \(y\)， \(z_1\) 的数量为 \(O(|\mathsf{Ball}(y)|)\)，但每个结点只会作为步骤二中的 \(y\) 出现 \(O(m/n)\) 次。
当 \(m/n = o(\log n)\) 时，可以验证 Section 4 里对于独立性的分析仍然成立，因为对于每个 \(v\) 满足 \(u \in V\backslash R_1\) 的 \(u\) 数量仍是 \(O(n^{o(1)})\) 的，其中 \(V\) 满足 \(V_{full}^{(v)}\cap V_{full}^{(u)}\) 。

因此，该算法的时间复杂度是 \(O(\frac n k\log n+mk+nk\log(mk/n))\)，当 \(m< n\log\log n\) 时，\(k\) 仍为 \(\sqrt{\frac{\log n}{\log\log n}}\)，时间复杂度下界为 \(O(n\sqrt{\log n\log\log n})\)；当 \(n\log\log n \le m < n\log n\) 时，令 \(k = \sqrt{\frac n m\log n}\)，时间复杂度下界将为 \(O(\sqrt{mn\log n})\)。