526互联

AcWing面试刷题模版总结

发布时间 2023-08-06 22:23:21作者: miseryjerry

目录

排序

快速排序模板

const int N=1e6+10;
int nums[N];

void quicksort(int *nums, int left, int right) {
    if(left >= right) return;
    int x=nums[left+right>>1], i=left-1, j=right+1;
    while(i < j) {
        do ++i; while(nums[i] < x);
        do --j; while(nums[j] > x);
        if(i < j) swap(nums[i], nums[j]);
    }
    quicksort(nums, left, j);
    quicksort(nums, j+1, right);
}
  • 上述模板也可x取nums[left]，其它不变
  • 若x取nums[right]，递归时参数范围选择时将(left, j)和(j+1, right)改为(left, i-1)和(i, right)
  • 若x取nums[left+right>>1]，递归时参数范围可(left, j)和(j+1, right)，也可(left, i-1)和(i, right)
  • 快速排序不稳定

归并排序模板

const int N=1e6+10;
int nums[N], tmp[N];

void mergesort(int *nums, int left, int right) {
    if(left >= right) return;
    
    int mid = left+right>>1;
    mergesort(nums, left, mid);
    mergesort(nums, mid+1, right);
    
    int k = 0, i = left, j = mid+1;
    while(i <= mid && j <= right) { //这里容易写成i < j 和快排搞混
        if(nums[i] <= nums[j]) tmp[k++] = nums[i++];
        else tmp[k++] = nums[j++];
    }
    while(i <= mid) tmp[k++] = nums[i++];
    while(j <= right) tmp[k++] = nums[j++];
    
    for(i = left, k = 0; i <= right; ++i, ++k) nums[i] = tmp[k];
}

主要思想：

  1. 确定分界点mid = (left+right)/2
  2. 递归处理左右两段
  3. 归并（双指针算法，指针表示剩余部分最小元素的位置）

在归并步骤时，如果碰到相同元素的插入，每次都选择第1段（左边）的元素插入，则能使归并算法稳定。

例题：逆序对的数量（使用归并排序）

-w935

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5+10;
int nums[N], tmp[N];

LL mergesort(int *nums, int left, int right) {
    if(left >= right) return 0;
    
    int mid = left+right>>1;
    LL res = mergesort(nums, left, mid) + mergesort(nums, mid+1, right);
    
    int k = 0, i = left, j = mid+1;
    while(i <= mid && j <= right) {
        if(nums[i] <= nums[j]) tmp[k++] = nums[i++]; //这里if <= 因为归并是稳定排序
        else {
            tmp[k++] = nums[j++];
            res += mid - i + 1; //这里是+=
        }
    }
    while(i <= mid) tmp[k++] = nums[i++];
    while(j <= right) tmp[k++] = nums[j++];
    
    for(i = left, k = 0; i <= right; ++i, ++k) nums[i] = tmp[k]; //注意这里<=right
    return res;
}

二分查找

整数二分模板

bool check(int x) {/*...*/} // 检查x是否满足某种性质

//区间[l, r]被划分成[l, mid]和[mid+1, r]时使用：
int bsearch_1(int l, int r) {
    while(l < r) {
        int mid = l+r>>1; // 若产生整数溢出 改为 l+(r-l>>1)
        if(check(mid)) r = mid; //check判断mid是否满足性质
        else l = mid+1;
    }
}

//区间[l, r]被划分成[l, mid-1]和[mid, r]时使用：
int bsearch_2(int l, int r) {
    while(l < r) {
        int mid = l+r+1>>1; // 若产生整数溢出 改为 l+(r+1-l>>1)
        if(check(mid)) l = mid;
        else r = mid-1;
    }
}

-w987
1是mid点落在红色部分的情况，且红色部分check为真；2是mid点落在绿色部分的情况，且绿色部分check为真

-w1062

例题：整数划分

-w951
-w945

#include <iostream>
using namespace std;

const int N=1e5+10;
int nums[N];

int n, q;

int main() {
    scanf("%d%d", &n, &q);
    for(int i = 0; i < n; ++i) scanf("%d", &nums[i]);
    
    while(q--) {
        int x;
        scanf("%d", &x);

         //找左边界
        int left = 0, right = n-1;
        while(left < right) {
            int mid = left+(right-left>>1);
            if(nums[mid] >= x) right = mid;
            else left = mid+1;
        }
        if(nums[left] != x) cout << "-1 -1" << endl; //说明未找到左边界
        else {
            //找到了左边界
            cout << left << " "; //打印左边界
            
            //找右边界
            int left = 0, right = n-1;
            while(left < right) {
                int mid = left+(right+1-left>>1);
                if(nums[mid] <= x) left = mid;
                else right = mid-1;
            }
            
            //只要找到左边界 最终若未找到右边界 left和right均指向左边界
            cout << left << endl; //cout << right << endl; //也可以
        }
        
    }
    return 0;
}

例题：x的平方根

-w882

模板解法（注意溢出）：

class Solution {
public:
    int mySqrt(int x) {
        int left = 0, right = x;
        while(left < right) {
            unsigned long long mid = (long)left + (long)right+ (long)1 >> 1;
            if(mid*mid <= x) left = mid;
            else right = mid-1;
        }
        return left;
    }
};

浮点数二分模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r) {
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    // 或者不用精度 只迭代100次即可
    // for(int i = 0; i < 100; ++i) {
    //     double mid = (l + r) / 2; //对于double类型这里应该除以2 而非移位
    //     if(check(mid)) r = mid;
    //     else l = mid;
    // }
    return l;
}

说明：

  • 浮点数二分不需要考虑mid是否+1，else后是否+1。
  • 没有固定的浮点数序列，因此要考虑精度eps，一般比题目要求多1位小数就行
  • 需要自己确定l和r的值，即查找范围

高精度、大整数运算

大整数比较模板

// A >= B返回true，否则返回false
bool cmp(vector<int>& A, vector<int>& B) {
    if (A.size() != B.size()) return A.size() > B.size();
    for (int i = A.size() - 1; i >= 0; i--) 
        if (A[i] != B[i])
            return A[i] > B[i];
    return true;
}

高精度加法模板

// C = A + B, A >= 0, B >= 0
vector<int> C;
vector<int> add(vector<int> &A, vector<int> &B) {
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i ++ ) {
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}

说明：

  • 模板假设A和B都是非负大整数
  • 大整数低位存放在数组低地址处，高位存放在数组高位处
  • 注意处理大整数的最高位进位
  • 读取数组时反向（n-1->0）遍历，运算时正向（0->n-1）遍历
  • 高精度加法不会出现前导0，而减法、乘法和除法会出现前导0

相关练习题目：
lc415、lc66、lc67、lc989

高精度减法模板

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B) {
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); ++i) {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);             // 涵盖t为正数负数两种情况
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();     // 去掉前导0，但不能把结果`0`去掉
    return C;
}

说明：

  • 模板假设A和B都是非负大整数，且\(A\ge B\)，可用cmp()模板判断是否满足\(A\ge B\)，不满足交换参数次序即可。
  • (t + 10) % 10涵盖了t正负两种情况：
    • \(t \ge 0\) 输出 t % 10
    • \(t \lt 0\) 输出 t + 10
  • 减法会产生多个前导0
  • 去掉前导0时，注意不能把结果0也去掉，即需要判断C.size() > 1

操作逻辑：

...
if(cmp(A, B)) {
    auto C = sub(A, B);
    for(int i=C.size()-1; i>=0; --i) printf("%d", C[i]);
} else {
    auto C = sub(B, A);
    printf("-"); // 负号
    for(int i=C.size()-1; i>=0; --i) printf("%d", C[i]);
}
...

高精度乘法模板

模板一：

// C = A * b, A >= 0, b > 0
vector<int> mul(vector<int> &A, int b) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; ++i) {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back(); // 去除前导0
    return C;
}

说明：

  • 模板假设A是非负大整数，b是基本类型int
  • 乘法模板把对最高位的进位的处理翻到了for的循环条件中，这是与加法的主要区别。加法之所以能用一个if就能解决最高位的进位问题，是因为高精度加法最高位进位不会超过10（实际上最多是1），而高精度乘法的最高位进位可能超过10，甚至更高，因此不能像加法那样处理

相关练习题目：
lc43

模板二：

// C = A * B, A >= 0, B >= 0
vector<int> mul(vector<int> &A, vector<int> &B) {
    int m = A.size(), n = B.size();
    vector<int> C(m+n);
    for(int i = 0; i < m; ++i)
        for(int j = 0; j < n; ++j)
            C[i+j] += A[i] * B[j];

    int t = 0;
    for(int i = 0; i < C.size(); ++i) {
        t += C[i];
        C[i] = t % 10;
        t /= 10;
    }
    while(C.size() > 1 && C.back() == 0) C.pop_back(); // 去除前导0
    return C;
}

说明：

  • 模板假设A、B均为非负大整数
  • 返回的C的存储方式同大整数加法

高精度除法模板

// A / b = C ... r, A >= 0, b > 0, r为余数
vector<int> div(vector<int> &A, int b, int &r) {
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; --i) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());            // #include <algorithm>
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

说明：

  • 模板假设A是非负大整数，b是基本类型int
  • 商用vector<int>保存，余数用参数r保存
  • 除法是反向遍历（高位到低位）
  • 结果要翻转，注意导入<algorithm>库
  • 注意遍历时，r = r * 10 + A[i];是=，而不是+=
  • 除法先算高位，为了与加减乘存储方式一致，返回的C的存储方式同大整数加法

前缀和与差分

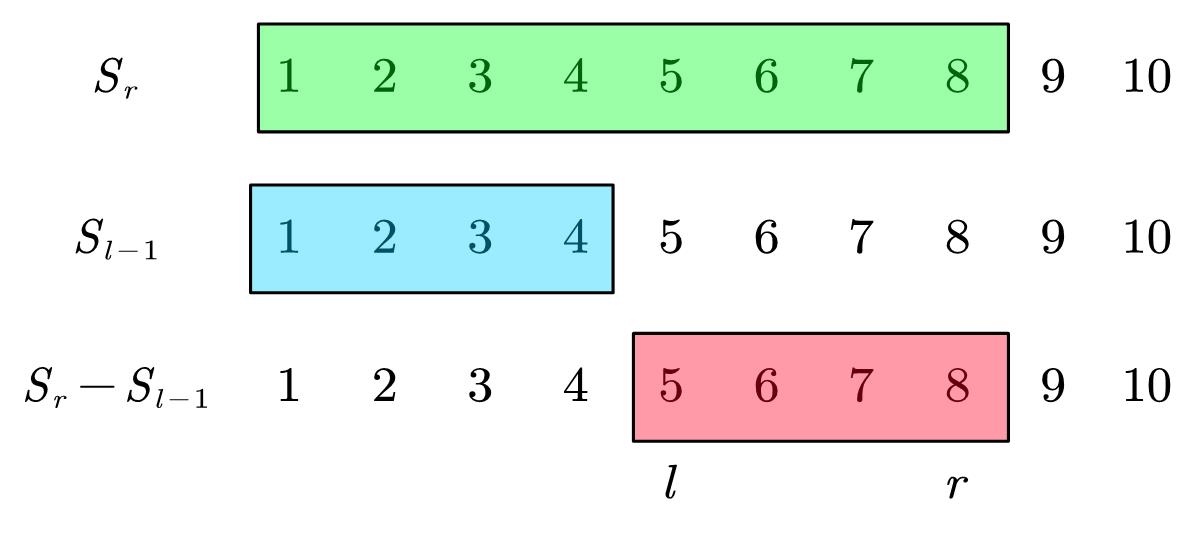
一维前缀和定义：

\[S_k = \sum\limits^k_{i=1} a_iS_0 = 0a_l+a_{l+1}+...+a_r = S_r - S_{l-1} \]

示意图：

一维前缀和模板

int a[N], S[N];

for (int i = 1; i <= n; ++i) S[i] = S[i - 1] + a[i];    // 给定数组a，初始化前缀和数组S
for (int i = 1; i <= n; ++i)  {
    scanf("%d", &a[i])          // 非必须
    S[i] = S[i - 1] + a[i];     // 未给定数组a，可合并读入和初始化的过程
}

printf("%d\n", S[r] - S[l-1]);    // 计算a[l] + ... + a[r]

说明：

  • 假设\(S_0 = a_0 = 0\)
  • 复杂度由O(n)降为O(1)
  • 数组a和S的第1个元素都不存储（下标为0），而从第2个元素开始存储（下标为1）
  • 注意遍历范围是1~n
  • 在一些不涉及a[i]的题目中，不必要存储a[i]的值，只需要存储S[i]就足够

相关练习题目：
lc53、lc1423、lc523

--

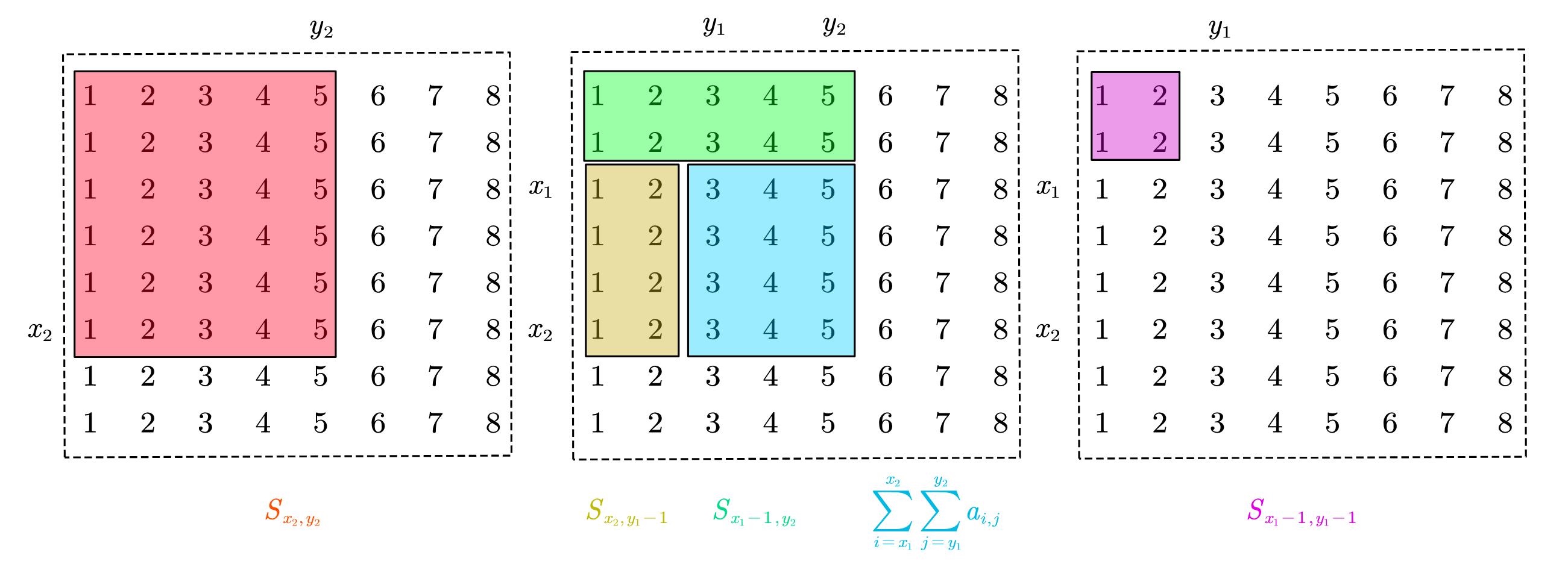
二维前缀和定义：

\[\begin{eqnarray}& S_{x,y} = \sum\limits^x_{i=1}\sum\limits^y_{j=1}a_{i,j} = S_{x-1,y} + S_{x,y-1} + S_{x-1,y-1} + a_{x,y}\tag{1} \\& S_{0,*} = S_{*,0} = a_{0, *} = 0 \tag{2} \\& \sum\limits^{x_2}\_{i=x_1} \sum\limits^{y_2}_{j=y_1}a_{i,j} = S_{x_2,y_
2}-S_{x_1-1,y_2}-S_{x_2,y_1-1}+S_{x_1-1,y_1-1}\tag{3} \end{eqnarray} \]

示意图：

二维前缀和模板

int a[N][N], S[N][N];

// 给定数组a
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++) 
        S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j];

// 没有给定数组a，需要读入并初始化前缀和数组，则可以合并读入和初始化的过程
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++) {
        scanf("%d", &a[i][j]);
        S[i][j] = S[i - 1][j] + S[i][j - 1] - S[ i - 1][j - 1] + a[i][j];
    }

// 使用
cout << S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2] + S[x1 - 1][y1 - 1] << endl;

说明：

  • 假设数组a中行下标或列下标为0的项都是0
  • 复杂度由O(m * n)降为O(1)
  • 读入数组a和初始化前缀和数组S的过程可以合并在一起
  • 注意遍历范围是1 ~ n
  • 在一些不涉及a[i][j]的题目中，不必要存储a[i][j]的值，只需要存储S[i][j]就足够

相关练习题目：
lc304

--

一维差分：给定区间[l, r]中的每个数加上c

构造方式：
存在 \(a_1, a_2, a_3, ..., a_n\)，构造 \(B_1, B_2, B_3, ..., B_n\)，使得 \(a_i = B_1 + B_2 + ... + B_i\)，\(a\) 数组是 \(B\) 数组的前缀和，一维构造很简单，让\(B_1 = a_1, B_2 = a_2 - a_1, B_3 = a_3 - a_2, ..., B_n = a_n-a_{n-1}\)。那么a数组就称为B 数组的前缀和数组，B数组就称为a数组的差分数组。

我们的目的是：使得a数组中某个区间的值统一加上c，那么首先构造B差分数组，对B差分数组以O(1)时间复杂度进行操作（比如对[l, r]区间的数均加上c，则B[l] += c; B[r+1] -= c;），操作完毕后通过B差分数组去计算出前缀和数组a，计算方法为B[i] += B[i-1]，进而得到区间[l, r]上统一加上c后的数组。（下述模板中的a数组并非前缀和数组，而是差分数组，这与上面构造方式说到的a和B含义不同，上述方式的a指的是前缀和，B指的是差分数组，但模板中的a指的是差分数组，B一开始存放差分元素值，修改后由转换为前缀和数组了。下述模板中将a的所有元素加入到B差分数组中，然后对B差分数组进行修改，修改后的结果转换为前缀和数组B[i] += B[i-1]，即可得到某个区间范围内值的统一加减后的前缀和数组）

一维差分模板

int a[N], B[N];

void insert(int l, int r, int c) {
    B[l] += c;
    B[r + 1] -= c;
}

// 初始化差分数组
for (int i = 1; i <= n; i++) {
    scanf("%d", &a[i]);
    insert(i, i, a[i]);
}

// 输出前缀和数组
for (int i = 1; i <= n; i++) {
    B[i] += B[i - 1];
    printf("%d ", B[i]);
}

说明：

  • 复杂度由O(n)降为O(1)
  • 用insert(i, i, a[i])与B[i] = a[i]初始化差分数组的区别在于，前者构造的差分数组B[n]等于-B[n - 1]，而后者等于0
  • 读入数组a和初始化差分数组B的过程可以合并在一起
  • 注意遍历范围是1 ~ n
  • 在一些不涉及a[i]的题目中，不必要存储a[i]的值，只需要存储S[i]就足够

例题：差分

-w779
-w713

#include <iostream>
using namespace std;

const int N = 1e5+10;
int n, m;
int a[N], B[N];

// [l, r]区间元素均加上c
void insert(int l, int r, int c) {
    B[l] += c;
    B[r+1] -= c;
}

int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    for(int i = 1; i <= n; ++i) insert(i, i, a[i]);
    while(m--) {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    for(int i = 1; i <= n; ++i) B[i] += B[i-1];
    for(int i = 1; i <= n; ++i) printf("%d ", B[i]);
    return 0;
}

--

二维差分：给\([x_1,y_1]\)（左上角点）与\([x_2,y_2]\)（右下角点）构成的矩形范围内的每个数加上c

二维差分模板

int B[N][N];            // 二维差分数组

void insert(int x1, int y1, int x2, int y2, int c) {
    B[x1][y1] += c;
    B[x2 + 1][y1] -= c;
    B[x1][y2 + 1] -= c;
    B[x2 + 1][y2 + 1] += c;
}

// 构造（无需额外的数组a）
int tmp;
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        scanf("%d", &tmp);
        insert(i, j, i, j, tmp);
    }
}

// 转换成二维前缀和数组
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
        B[i][j] += B[i - 1][j] + B[i][j - 1] - B[i - 1][j - 1];

说明：

  • insert()函数规律
  • 下标出现2的部分都+1
  • 范围最大最小的+=c，其它-=c
  • 复杂度由O(m * n)降为O(1)
  • 注意遍历范围是1 ~ n

双指针算法

定义：

  • 第1类双指针算法：一个指针操作一个序列（归并排序的合并步骤）
  • 第2类双指针算法：两个指针操作同一个序列（快速排序）

双指针算法模板

for(int i = 0, j = 0; i < n; ++i) {
    while (j < i && check(i, j)) j++;
    // 题目逻辑
}

说明：

  • 目的是把\(O(n^2)\)复杂度降为\(O(n)\)
  • 双指针算法会把序列分成3段，理解各段的含义很重要（尤其第2段）
    • 第1段：0 ~ j-1
    • 第2段：j ~ i
    • 第3段：i+1 ~ n-1

例题

-w750

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int n = s.size();
        int res = 0;
        int a[200] = {0};
        for(int i = 0, j = 0; i < n; ++i) {
            a[s[i]]++;
            while(a[s[i]] > 1) {
                a[s[j]]--;
                j++;
            }
            res = max(res, i-j+1);
        }
        return res;
    }
};

位运算

要点：

  • x & -x返回最后1位1，例如101000返回1000，这个lowbit操作是树状数组的基本操作
  • x >> k && 1返回x右起第k位二进制数

位运算模板

// 返回最后一位1，例如101000返回1000
int lowbit(int x) {
    return x & -x;  // 或者return x&(~x+1);
}

// 统计某数x二进制1的个数
int cnt = 0;
while(x) {
    x -= lowbit(x);
    ++cnt;          // cnt记录x的二进制中1的个数
}

// 打印数x的二进制表示
for(int i = 31; i >= 0; --i) cout << (x>>i & 1);

说明：

  • 若让x不停地减去最后1位1，直到变成0，做减法的次数就是x二进制表示的1的个数

例题

-w595

class Solution {
public:
    int lowbit(int x) {
        return x & -x;
    }
    vector<int> countBits(int n) {
        vector<int> res;
        for(int i = 0; i <= n; ++i) {
            int cnt = 0;
            int x = i;
            while(x) x -= lowbit(x), ++cnt;
            res.push_back(cnt);
        }
        return res;
    }
};

相关题目：
lc190、lc191、lc78

离散化

适用问题：需要开辟长度很大的数组统计数据（\(10^9\)），但实际上使用的元素个数很少（\(10^5\)）

离散化模板

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // +1是为了映射到1, 2, ...n，而非0, 1, 2, ..., n-1
}

说明：

  • 实际上解决的是稀疏数组表示的问题，本质是映射问题
  • 先把元素存储在vector<int> alls中，排序去重后，再把值映射到长度较小的数组a中
  • 通过二分查找find(x)找到元素x在数组a的下标
  • 排序去重后的alls与数组a的相对顺序是一致的
  • 二分查找是整数二分的特例

例题：区间和

-w826-w759

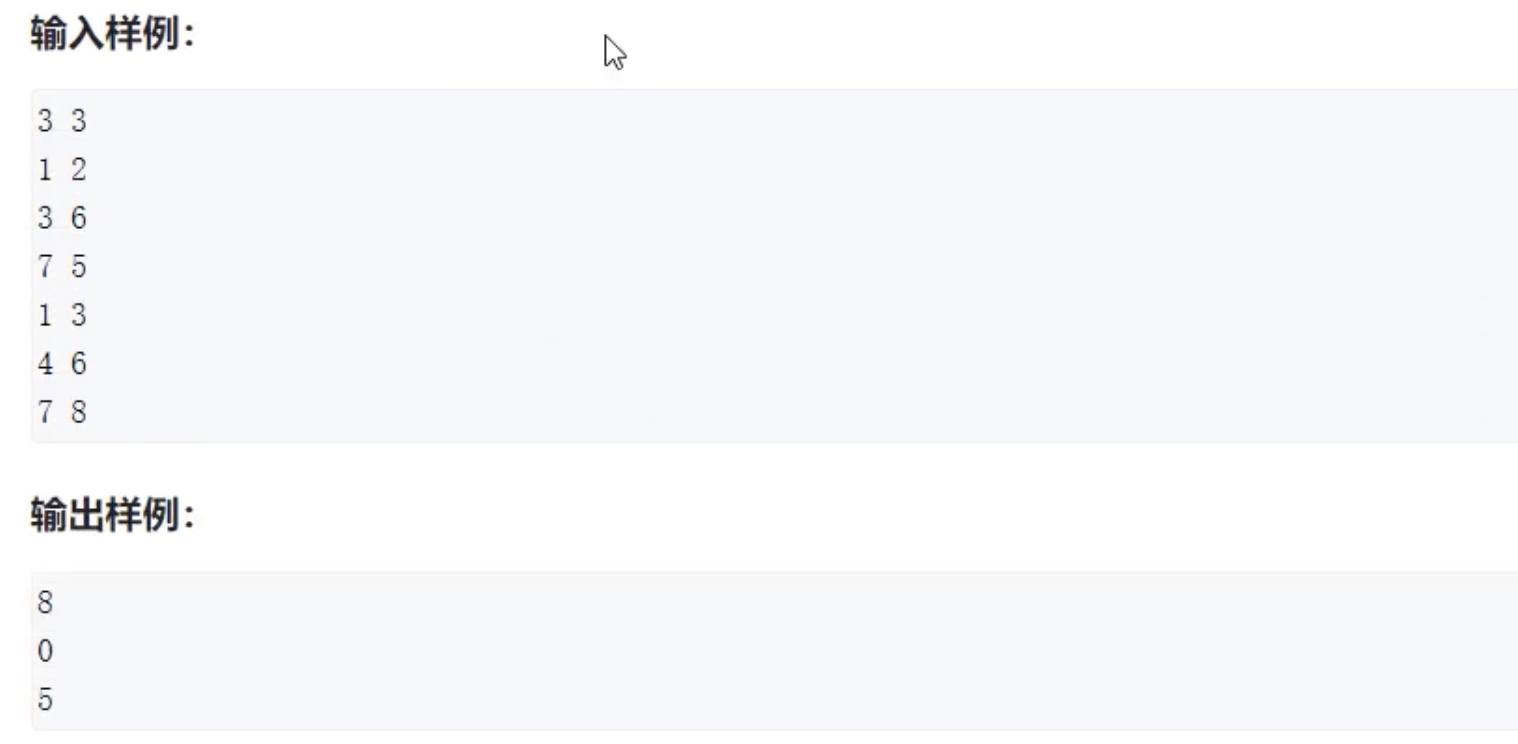
这道题若数组范围较小时可用前缀和做，若数组范围较大则需用离散化去解决。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 300010;
int n, m;
int a[N], s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x) {
    int l = 0, r = alls.size()-1;
    while(l < r) {
        int mid = l+r >> 1;
        if(alls[mid] >= x) {
            r = x;
        } else {
            l = mid+1;
        }
    }
    return r+1;
}

int main() {
    cin >> n >> m;
    for(int i = 0; i < n; ++i) {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        
        alls.push_back(x);
    }
    
    for(int i = 0; i < m; ++i) {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});
        
        alls.push_back(l);
        alls.push_back(r);
    }
    
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    for(auto item : add) {
        int x = find(item.first);
        a[x] += item.second;
    }
    
    // 预处理前缀和
    for(int i = 1; i <= alls.size(); ++i) s[i] = s[i-1] + a[i];
    
    // 处理询问
    for(auto item : query) {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l-1] << endl;
    }
    return 0;
}

区间合并

适用问题：把若干个区间合并成多个没有交集的区间。

区间合并模板

typedef pair<int, int> PII;

// 将所有存在交集的区间合并
void merge(vector<PII> &segs) {
    vector<PII> res;    // 存储合并结果
    sort(segs.begin(), segs.end()); // pair默认优先左端点排序，再右端点排序

    int st = -2e9, ed = -2e9;       // 左端点最小值
    for(auto seg : segs) {
        if(ed < seg.first) {
            if(st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        } else {
            ed = max(ed, seg.second);
        }
    }
    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

说明：

  • 先按左端点排序，然后再合并
  • 选取第2个区间时，可分为两大类情况
    • 有交集（包括“包含”和“相交但不包含”两种情况）
    • 无交集
  • 对于有交集的情况，只需保留最大的右端点即可
  • 对于无交集的情况，首先判断是否是空区间（st == -2e9），非空则保存当前区间，并跳至下一个区间
  • 由于循环内部是先发现新的无交集区间才保存当前指向的区间，因此在循环结束后，还需要单独保存当前区间（注意判断是否为空区间）

链表

单链表模板

int e[N], ne[N]; // 链表元素及下个结点的地址
int head;       // 头结点地址
int idx;        // 可用位置

/** 创建含头结点的单链表 */
void init() {
    head = 0;

    // 头结点
    e[0] = 0;       // 值为链表长度
    ne[0] = -1;     

    idx = 1;        // 第1个结点的下标从1开始
}

/** 向链表头部插入一个数 */
void insert_head(int x) {
    e[idx] = x;
    ne[idx] = ne[head];
    ne[head] = idx;
    idx++;

    e[0]++;     // 链表长度+1
}

/** 删除下标为k后面的数 */
void rem(int k) {
    ne[k] = ne[ne[k]];
    e[0]--;     // 链表长度-1
}

/** 在下标为k的位置后插入一个数 */
void insert(int k, int x) {
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx++;

    e[0]++;     // 链表长度+1
}

/** 遍历链表 */
void print() {
    for (int i = ne[head]; i != -1; i = ne[i]) cout << e[i] << " ";
}

说明：

  • 采用含头结点的单链表，头结点存储链表长度
  • 元素从下标1开始存储

双链表模板

const int N = 100010;
int e[N], l[N], r[N], idx;

/** 创建双链表（含头结点和尾结点） */
void init() {
    r[0] = 1;       // 头结点
    l[1] = 0;       // 尾结点
    idx = 2;
}

/** 在下标为k的结点右侧插入一个结点 */
void insert(int k, int x) {
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx;
    idx++;
}

/** 删除下标为k的结点 */
void remove(int k) {
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

/** 输出 */
void print() {
    for (int i = r[0]; i != 1; i = r[i]) printf("%d ", e[i]);
}

说明：

  • 实现的双链表含头结点和尾结点，下标分别为0和1
  • insert()函数可根据参数的选取实现在链表任意位置插入的功能（包括头插和尾插）
  • 遍历时从头结点的下一个位置开始（r[0]），直到遍历到尾结点（下标为0）

栈与队列

栈模板

int stk[N], tt = 0;     // tt表示栈顶

// 向栈顶插入一个数
stk[++tt] = x;

// 从栈顶弹出一个数
--tt;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if(tt) {...}       // 栈不为空

说明：

  • 栈从下标1开始存储元素
  • 栈指针tt的值可表示栈的实际长度

普通队列模板

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[++tt] = x;

// 从队头弹出一个数
++hh;

// 队头的值
q[hh];

// 判断队列是否为空
if(hh > tt) {...}   // 队列为空

说明：

  • tt + 1 - hh可表示队列长度

循环队列模板

// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if(tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if(hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空
if(hh == tt) {...}

说明：

  • 这种实现方式与普通队列方式有点区别，在这里是先存入，后++，故tt初值为0
  • 可以把入队改成q[tt] = x; tt = (tt + 1) % N;，出队改成hh = (hh + 1) % N; x = q[hh];
  • 队满判断可用(tt + 1) % N == hh
  • 队列长度可用(tt - hh + N) % N求出

单调栈模板

int tt = 0;
for(int i = 1; i <= n; ++i) {
    while(tt && check(stk[tt], i)) --tt;
    stk[ ++ tt] = i;
}

用途
为每个数找出满足如下条件的数:

  • 在它左边
  • 距离最近
  • 比它小（大）

说明：时间复杂度由 \(O(n^2)\) 降为 \(O(n)\)。当要找比当前值小的最近左值，那只需要在从左向右遍历时，若遇到左边的值大于右边的值时（局部递减），将左边的值删除掉即可，在代码中的展现就如下面例题代码中满足tt && stk[tt] >= x就进行--tt。

例题：单调栈

-w812

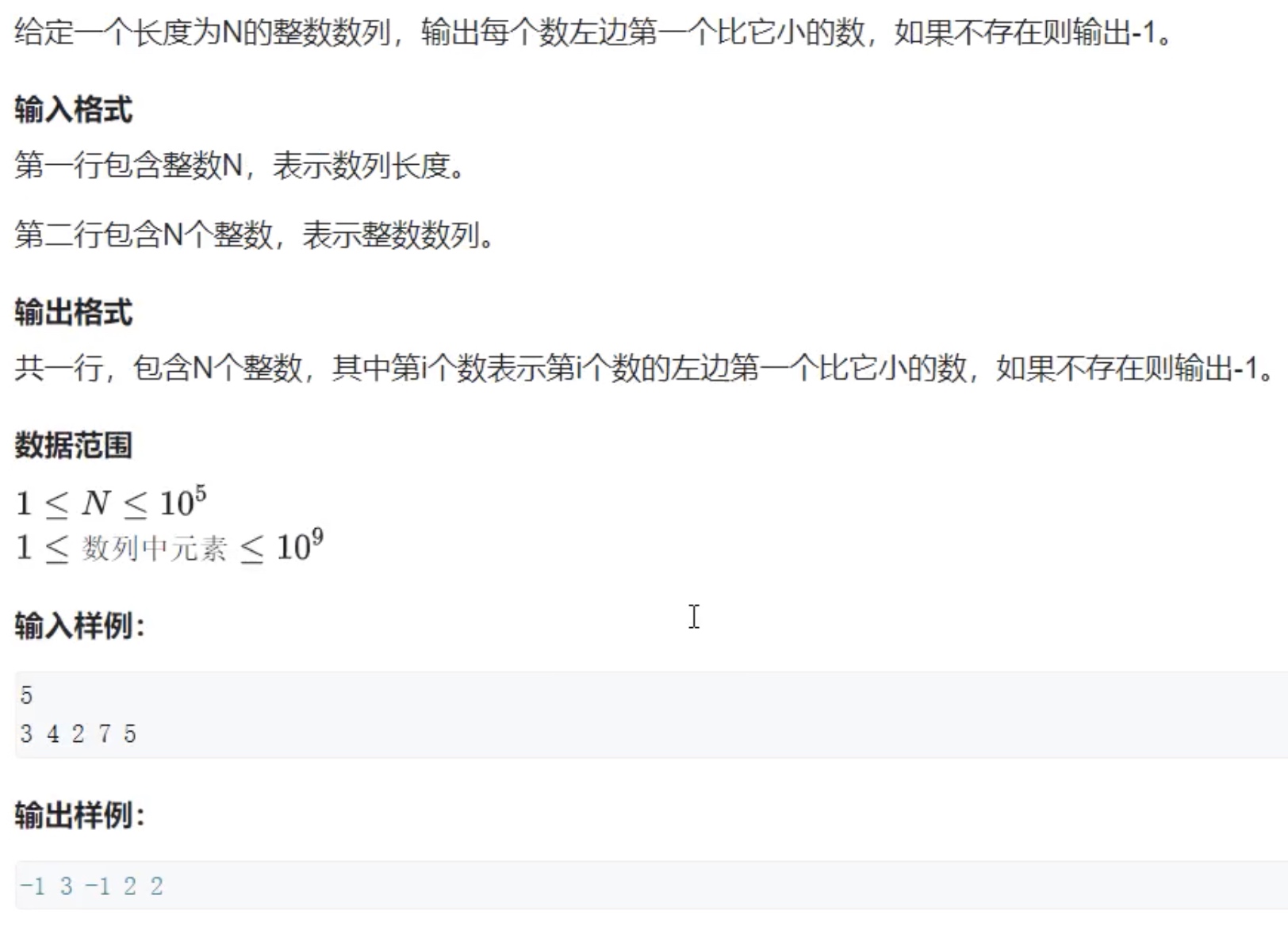
#include <iostream>
using namespace std;
const int N = 1e5+10;

int stk[N], x;
int tt = 0;
int main () {
    int n;
    cin >> n;
    for(int i = 0; i < n; ++i) {
        int x;
        cin >> x;
        while(tt && stk[tt] >= x) {
            --tt;
        }

        if(tt) cout << stk[tt] << " ";  // 找到了左边比x小的数
        else cout << -1 << " "; // 说明没找到

        stk[++tt] = x;
    }
    return 0;
}

注意，上述代码输入输出换成scanf、printf效率更高

单调队列模板

用途：找出滑动窗口中的最大值（最小值）

int hh = 0, tt = -1;
for(int i = 0; i < n; i ++ ) {
    while(hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while(hh <= tt && check(q[tt], i)) tt -- ;  // check使得满足某种单调性
    q[ ++ tt] = i;
}

说明：时间复杂度由 \(O(nk)\) 降为 \(O(n+k)\)

例题：

单调栈存储具体的值，单调队列存储索引。

Trie树

用途：

快速存储和查找字符串集合，又称字典树

模板：

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) son[p][u] = ++ idx; // 不存在结点则创建结点
p = son[p][u]; // 指向新结点
}
cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
说明：

Trie树共享前缀，结点存在不代表根到该结点的字符串存在，需要看标记数组cnt
Trie树是多重集合
son数组的第1维表示结点地址，要大于所有存储的字符串长度的和（不是字符串长度的最大值）；第2维表示每个结点的最大分支数，一般取字符种类数（如小写字母有26个）
cnt[i]表示以son[i]结点为末尾的字符串的个数

刷题总结

  • 判断两个字母是否为同一个字母的大小写：x^y == 32
  • 做01背包的时候划分左右区间，通常需要判断sum%2 == 1成立于否，条件可改为sum & 1
  • 多重背包可以用单调队列优化（讲单调队列时提到的，后续再考虑下）