初始化?
给定一个字符串,求其最长回文串,比如:
aababa,最长回文长度为 3,是ababa;
abbabb,最长回文长度为 2,是abba;
以上两个回文串有奇回文和偶回文,这样处理比较繁琐,需要我们进行分类讨论。
所以我们第一步就是先将字符串统一处理为奇回文。
也就是将每两个字符串之间插入一个占位符(随便吧,我用的是 #),强制将所有的都改为奇回文串,然后再在前面和后面各加入一个不同的字符,防止越界。
e.g.我们可以将aababa变换为@#a#a#b#a#b#a#%。
Code
int p=0;
s[p]='@';s[++p]='#';
for(int i=1;i<=n;++i){
s[++p]=t[i];
s[++p]='#';
}
s[p+1]='%';
实现?
对于正常的暴力,大概是 \(O(n^3)\) 的,不过你优化一下,你大概可以优化到 \(O(n^2)\)。
那么暴力就有一个致命的缺陷:每次求完一个回文串后,什么信息都不能继承,导致需要重新算一遍,这就很费时间好吧,则我们需要考虑一下,之前已经求出来的信息,能不能用在这次呢?
显然是可以的。
我们可以定义一个数组 \(p\),\(p_i\) 表示 \(i\) 所在的字符为中心的最长回文的半径。
且可以发现一个性质,就是我们插入那些占位符的 \(p_i\) 是奇数,而原串中的字符的 \(p_i\) 都是偶数。(似乎没什么用)
并且我们记录一个 \(mid\),表示在i之前所有的回文中心中,回文右端点最远在哪,记 \(mx\) 表示这个最远的右端点所对应的回文中心
接下来,我们考虑如何用这个东西维护 \(p_i\)
这是需要分类讨论的,即:
- 当 \(mid<i<mx\) 时,情况如下图:
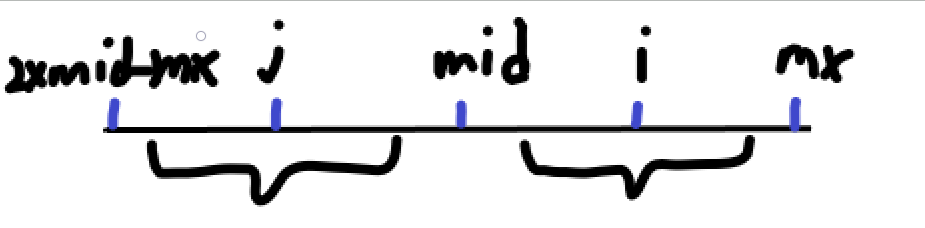
我们可以在 \(mid\) 的另一边找到 \(i\) 的一个对称点 \(j\),那么 \([i-p_j,i+p_j]=[j-p_j,j+p_j]\)。但是要注意一下边界情况,回文的长度应该不超过 \(mid\times 2-mx\)(\(mx-i\) 也是一样的),毕竟超过了就不能保证它相等了。
所以对于这种情况,我们可以将 \(p_i\) 的初值设为:\(min(p_{mid\times 2-i},mx-i)\)。然后暴力拓展即可。
- 当 \(i>mx\) 时:
我们找不到对称点,只能暴力拓展。
最后考虑如何更新 \(mid\) 与 \(mx\):
我们需要能继承的越多,那尽量要多些第一种情况,那么当我们遇到某个右端点比 \(mx\) 大的时候,就可以更新了。
将 \(mid\to i,mx\to i+p_i\) 即可。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=22000005;
inline int read(){
int x=0,f=1;
char ch;
ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*f;
}
int n;
char s[N],t[N];
int p[N];
void manacher(){
s[0]='@';
int q=0;
s[++q]='#';
for(int i=0;i<n;++i){
s[++q]=t[i];
s[++q]='#';
}
s[q+1]='%';//初始化
int mx=0,mid=0;
for(int i=1;i<=q;i++){
if(i<mx) p[i]=min(p[mid*2-i],mx-i);//继承
while(s[i+p[i]+1]==s[i-p[i]-1]) ++p[i];//暴力拓展
if(p[i]+i>mx) mx=i+p[i],mid=i;//更新
}
}
signed main(){
cin>>t;
n=strlen(t);
manacher();
int ans=0;
for(int i=1;i<=2*n+1;++i)
ans=max(ans,p[i]);
cout<<ans;
return 0;
}