Prufer 序列
Prufer 序列可以将一个带标号 \(n\) 个节点的树用 \([1,n]\) 中的 \(n-2\) 个整数表示,即 \(n\) 个点的完全图的生成树与长度为 \(n-2\) 值域为 \([1,n]\) 的数列构成的双射。
Prufer 序列可以方便的解决一类树相关的计数问题,比如凯莱定理:\(n\) 个点的完全图的生成树有 \(n^{n-2}\) 个。
对树构造 Prufer 序列
\(Prufer\) 序列 是这样构造的:
每次选择一个编号最小的叶节点并删掉它,然后在序列中记录下它连接到的那个节点。
过程
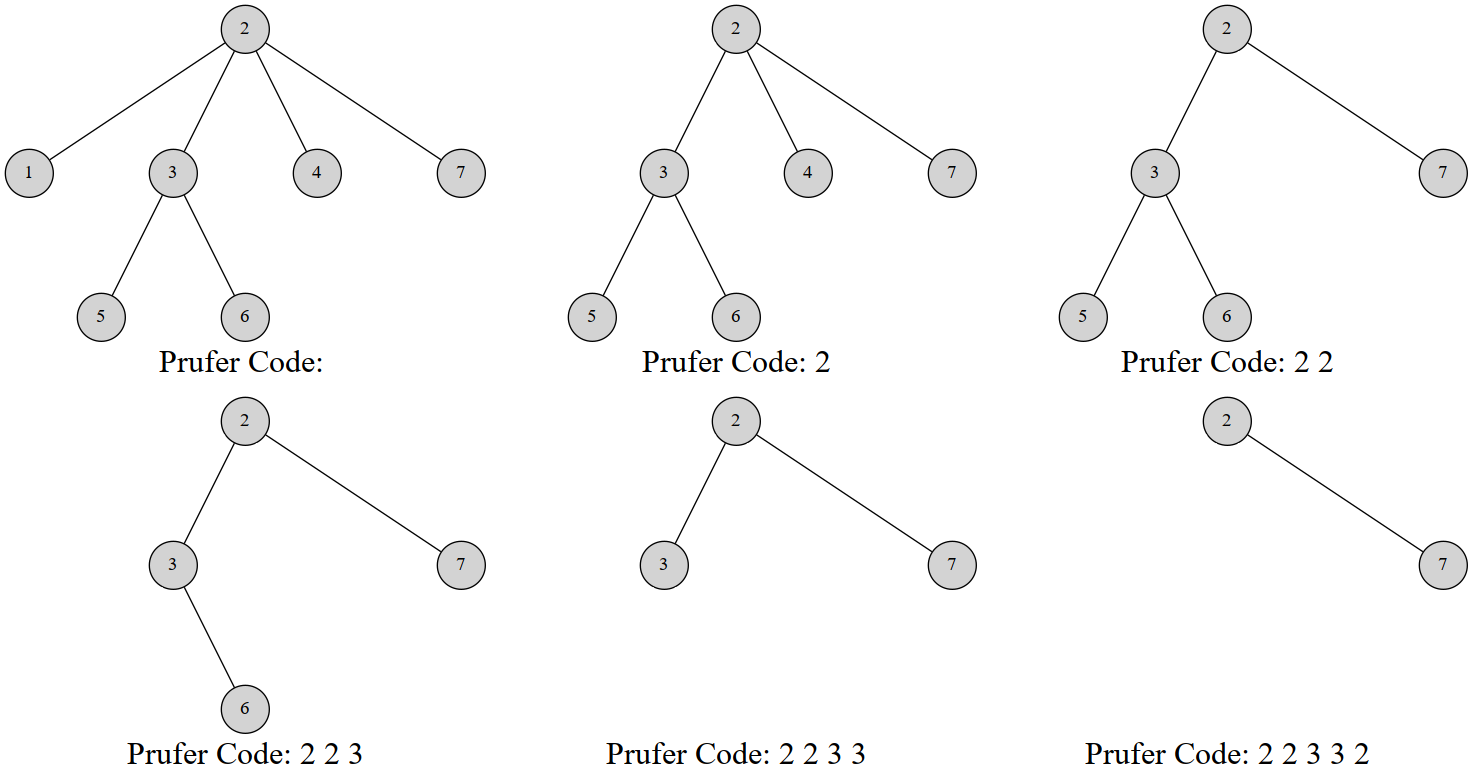
重复 \(n-2\) 次后就只剩下两个节点,算法结束。
\(\mathcal O(n \log n)\)
显然,使用堆可以做到 $ O(n\log n)$ 的复杂度。
\(\mathcal O(n)\)
使用一个指针代替堆找最小值,可以做到 \(\mathcal O(n)\) 的复杂度。
具体而言,指针指向编号最小的叶节点。每次删掉它之后,如果产生了新的叶节点且编号比指针指向的更小,则直接继续删掉,否则自增找到下一个编号最小的叶节点。
循环上述操作$n-2 $ 次,就完成了序列的构造。接下来考虑算法的正确性。
\(p\) 是当前编号最小的叶结点,若删除 \(p\) 后未产生叶结点,我们就只能去寻找下一个叶结点;若产生了叶结点 \(x\):
- 如果 \(x > p\),则反正 \(p\) 往后扫描都会扫到它,于是不做操作;
- 如果 \(x < p\),因为 \(p\) 原本就是编号最小的,而 \(x\) 比 \(p\) 还小,所以 \(x\) 就是当前编号最小的叶结点,优先删除。删除 继续这样的考虑直到没有更小的叶结点。
算法复杂度分析,发现每条边最多被访问一次(在删度数的时侯),而指针最多遍历每个结点一次,因此复杂度是 \(O(n)\) 的。
具体实现
void solve1(){
for(int i=1;i<n;++i) f[i]=read(),++d[f[i]];
for(int i=1,j=1;i<=n-2;++i,++j){
while(d[j]) ++j;p[i]=f[j];
while(i<=n-2&&!(--d[p[i]])&&p[i]<j) p[i+1]=f[p[i]],++i;
}
}
用 Prufer 序列构造树
根据 Prufer 序列的性质,我们可以得到原树上每个点的度数。
每次我们选择一个编号最小的度数为$ 1$ 的节点,与当前枚举到的 Prufer 序列的点连接,然后同时减掉两个点的度数。重复 \(n-2\) 次后就只剩下两个度数为 \(1\) 的节点,其中一个是 \(n\),把它们连接起来即可。
\(\mathcal O(n \log n)\)
同样地,显然,使用堆可以做到 \(O(n\log n)\) 的复杂度。
\(\mathcal O(n)\)
类似地,使用一个指针代替堆找最小值,可以做到 \(\mathcal O(n)\) 的复杂度。
具体而言,指针指向编号最小的度数为 \(1\)的节点。每次将它与当前枚举到的 Prufer 序列的点连接之后,如果产生了新的度数为$ 1$ 的节点且编号比指针指向的更小,则直接继续将它与下一个 Prufer 序列的点连接,否则自增找到下一个编号最小的度数为 \(1\) 的节点。
具体实现
void solve2(){
for(int i=1;i<n-1;++i) p[i]=read(),++d[p[i]];p[n-1]=n;
for(int i=1,j=1;i<n;++i,++j){
while(d[j]) ++j;f[j]=p[i];
while(i<n&&!(--d[p[i]])&&p[i]<j) f[p[i]]=p[i+1],++i;
}
}
通过这些过程其实可以理解,\(Prufer\) 序列与带标号无根树建立了双射关系。
prufer 序列的一些性质
1.与一棵有标号的无根树对应
2.某编号结点的入度为该点在prufer 序列中出现的次数 \(+1\)
3.点数为 \(n\) 的有标号无根树个数为 \(n^{n-2}\)
,有根树当然就 \(\times n\) 就行啦。
4.每个点度数为 \(d_i\)
的有标号无根树个数为 \(\frac{(n-2)!}{\prod\limits_{i=1}^n(d_i-1)!}\)
#include<bits/stdc++.h>
#define N 5000005
#define int long long
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int n,m,ans;
int f[N],p[N],d[N];
void solve1(){
for(int i=1;i<n;++i) f[i]=read(),++d[f[i]];
for(int i=1,j=1;i<=n-2;++i,++j){
while(d[j]) ++j;p[i]=f[j];
while(i<=n-2&&!(--d[p[i]])&&p[i]<j) p[i+1]=f[p[i]],++i;
}
for(int i=1;i<=n-2;++i) ans^=i*p[i];
}
void solve2(){
for(int i=1;i<n-1;++i) p[i]=read(),++d[p[i]];p[n-1]=n;
for(int i=1,j=1;i<n;++i,++j){
while(d[j]) ++j;f[j]=p[i];
while(i<n&&!(--d[p[i]])&&p[i]<j) f[p[i]]=p[i+1],++i;
}
for(int i=1;i<n;++i) ans^=i*f[i];
}
signed main(){
n=read(),m=read();
m==1?solve1():solve2();
printf("%lld\n",ans);
return 0;
}
#include<bits/stdc++.h>
#define N 205
#define int long long
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int n,ans=1,sum;
int d[N],c[N][N];
signed main(){
n=read();
for(int i=1;i<=n;++i) d[i]=read();
if(n==1){
if(d[1]==0) printf("1\n");
else printf("0\n");
return 0;
}
for(int i=0;i<=n;++i){
c[i][0]=1;
for(int j=1;j<=i;++j) c[i][j]=c[i-1][j]+c[i-1][j-1];
}
for(int i=1;i<=n;++i){
if(!d[i]) return printf("0\n"),0;
d[i]--;
sum+=d[i];
}
if(sum!=n-2) return printf("0\n"),0;
sum=0;
for(int i=1;i<=n;++i) ans*=c[n-2-sum][d[i]],sum+=d[i];
printf("%lld\n",ans);
return 0;
}
Cayley 公式 (Cayley's formula)
完全图 \(K_n\) 有 \(n^{n-2}\) 棵生成树。
怎么证明?方法很多,但是用 Prufer 序列证是很简单的。任意一个长度为 \(n-2\) 的值域 \([1,n]\) 的整数序列都可以通过 Prufer 序列双射对应一个生成树,于是方案数就是 \(n^{n-2}\)。