[AHOI2013] 作业

区间求值域在$[a,b]$的数的个数和种类

由于有$O(n\sqrt m)$复杂度的修改和$O(m)$的查询，我们需要$O(1)$修改，$O(\sqrt n)$查询的东西，自然是

分块。

于是考虑值域分块即可。

[P3709] 大爷的字符串题

询问一个区间能被拆成至少几个(严格的)$LIS$ （求区间众数的出现次数）

等价于：给你 $n$ 个数, $m$ 次询问区间 $[l,r]$ 中众数的出现次数。

然后就是区间众数的处理方法。

$cnt[i]$ 表示数 $i$ 出现的次数, $t[i]$ 表示出现 $i$ 次的数有多少个。

加入一个数时,把 $Ans$ 和 $cnt$ 取个$Max$。

删除一个数时,如果有$t[cnt]==1$ && $cnt==Ans$，那么就 $Ans−−$

小清新人渣本愿

区间求是否有：和，差，积为$x$的一对数

$bitset$，判断$S$ & $(S>>x)$，和的话可以维护一个倒着的$bitset$。

模拟赛 29 B

给定一棵树和序列，区间跳$father$，区间求$min_{l≤i≤r}$ $dep(a_i)$

分块，让每个块至多总共跳$n$次以来均摊复杂度，所以如果一个块内的点同时跳的时候遇到了之前

跳到过的点就别跳了。

时间复杂度分析：对于一次散块修改，首先$\sqrt n\times log(n)$还原块，再$\sqrt n$暴力跳父亲，然后$\sqrt n$修

改$vector$，对于整块修改，其总共不会超过$O(n)$，总共有$\sqrt n$个块，所以总共是$O(n\times \sqrt n)$的。

总共修改的散块个数是$2\times n$的，也就是说就算$vector$要重构也总共只用重构$2\times n\times \sqrt n$的。

[HEOI2015] 公约数数列

将 $a_i$ 修改为 $x$.

求最小的整数 $p(0≤p<n)$，使得 $gcd(a0,a1,...,ap)\times XOR(a0,a1,...,ap)=x$

首先注意到前缀 $gcd$ 种类不超过 $log$ 个，所以产生变化的位置甚至可以枚举。

然后我们从前往后枚举，对于 $gcd$ 不变的整块，只需要用 $map$ 找到有无异或前缀和等于 $x/gcd$。

单点修改？只用**修改当前块的 $map$ **

原因在于，修改是$10000$的，查询是$10000$的，我们希望做到查询修改都是 $\sqrt n$的，所以我们只能

修改一个块的$map$，查询的时候每经过一个块就再 $xor$ 一次总块。

如果一个块内出现了不同的 $gcd$ 就暴力扫块，然后至多有 $log$ 个块要暴力扫。

P3603 雪辉

给定一棵树，求链的并的点权种类以及$mex$

~~太强了太强了~~

看到 $mex$ 和数颜色可以想到 $bitset$，然后直觉上是每个链维护一个$bitset$然后合并。

也就是一颗线段树，所有的 $nlogn$ 个节点中，每个点有一个 $bitset$，这样做空间开不下。

然后发现这很类似于线段树合并，底部的两层几乎只有$1,2$个数，于是下两层用$pair$存。

线段树的节点分布：$2^0+2^1+...2^k$满足$2^k\ge n$，那么去掉最后一行就最多只有$n$个节点

也就是：线段树的节点个数 $-$ 最后一行的节点个数 $\approx$ n

[AT_joisc2014_c]歴史の研究

询问区间最大的$val\times time$ （值乘上出现次数）

首选想到莫队，然后伸展很好做，缩小很难做，那么采用回滚莫队

注意，在操作的时候，要先把单独右边的贡献给记录到 $lst$ 里面，然后再移动左端点，这样在左端

点移动回来的时候才能正确初始答案。

这个时候的排序要格外注意了，就必须严格用 $belong$ 了。

[ZJOI2013]K大数查询

1 l r c：表示将 $c$ 加入到编号在 $[l,r]$ 内的集合中

2 l r c：表示查询编号在 $[l,r]$ 内的集合的并集中，第 $c$ 大的数是多少。

采用树套树，先在外层套一个权值线段树，每一个点存当前权值在哪些集合里面出现过，这个用动态开点线段树然

后查询的时候就在最外层的权值线段树上二分就可以了。

CF620E

其实原题挺简单的，拿$bitset$就能做了，但是如果$a[i]$达到了 $100$ 怎么做呢？

我们可以考虑把$100$ 拆分成前$50$和后$50$，就能做了。

P4145 上帝造题的7分钟 2

区间开根，区间询问和

做法简单，一个数开根$log$次就会变成$1$，然后就不会变了，于是考虑维护区间最大值，如果最大值不超过$1$就不要

递归下去了。

这道题的关键在于时间复杂度的分析，我们直接分析每一次操作的复杂度是很难的，于是我们换一个角度考虑，我

们发现所有$n$个数，每个数都至多会被操作$6$次，我们假设每一次操作都是单点修改，会带上$log$ ，于是严谨一些的

总复杂度为$O(6\times n\times logn)$了。

区间的有些操作虽然难以维护，但是可以通过操作的性质对于区间进行合并处理。

完全合并需要的次数（即总势能）只要在可接受范围内，那么这个暴力修改+剪枝的做法就是可以接受的。

UOJ228 基础数据结构练习题

区间加，区间开根，区间求和

记录区间内$max,min$，开根号时，判断$min-\sqrt min$是否等于$max-\sqrt max$，如果等于，等价于区间加一个

负数值，如果不等直接继续递归。

原因在于开根会导致$max-min \rightarrow \sqrt max-\sqrt min$ ，其实也就是极差除以$\sqrt max+\sqrt min$，

至于时间复杂度，我们这样考虑它，如果有一个区间里的数全部都相等，那么我们其实是可以$O(1)$的打上加减标

记的，如果没有加法，那么最多进行 $6nlogn$ 次操作序列就会全部变成$1$，但很不幸的是我们有区间加法操作，但

是每次区间加法操作只会使得$2logn$个区间的$min-\sqrt min$和$max-\sqrt max$产生改变，我们又需要对于每一个

这样的区间执行$6$次的修改，所以每次区间加法造成的影响是 $2\times 6 \times logn$的，所以是$log^2n$的，加法操作是

$nlogn$的，所以大致复杂度是$nlog^2n$的。

CF438D The Child and Sequence

区间取模，区间求和，单点修改

这道题其实也隐藏了 $log$ 的性质，具体的：$ x mod p < \frac{x}{2}$。

所以我们可以照葫芦画瓢，记录区间最大值，再加上单点修改，然后同花神游历各国就行了，唯一的区别在于复杂

度，花游是$6nlogn$，这一个是$nlog^2n$的，对于单点加操作的理解同上一题。

CF431E Chemistry Experiment

$1$ $p$ $x$：倒掉试管$p$的水银修改为$x$ $ml$。

$2$ $v$：将$v$ $ml$水任意分配至$n$支试管里，最小化有水的试管中最大体积，输出这个最小值，误差不超过$10^{-4}$算作正确。。这个操作只是一次假想，不会真的把水倒进试管里。

直接二分答案 $mid$，判断可不可行就线段树查询值域小于$mid$的值的和，然后用

$mid\times num$减去，再看是否大于 $v$ 就可以了，要注意的是这题需要动态开点的线段树。

P2184 贪婪大陆

每次操作会加入新的线段，问有多少条线段与区间相交

注意是不能直接取 $max$ 的，因为会遇到这种情况：

这个时候，我们其实可以维护两个东西：

维护节点$i$，之前有几个线段的开头，设为$st(i)$。
维护节点$i$，之前有几个线段的结尾，设为$ed(i)$。

那么实际询问要求的就是 $st[r]-ed[l-1]$。

P1438 无聊的数列

区间加等差数列，单点查询

我们发现等差数列这个东西是可合并的，也就是：

一个首项为$A$，公差为$B$的数列，加上一个首项为$C$，为$D$的数列可以合成一个首项为

$A+C$，公差为$B+D$的序列。于是我们在线段树上记录首项和公差即可。

----------------------------------------------一次复习分割线--------------------------------------------------

CF992E Nastya and King-Shamans

给定一个序列 $a_i$ ，记其前缀和序列为 $s_i$ ，有 $q$ 个询问，每次单点修改，询问是否存在一个 $i$ 满足 $a_i=s_{i-1}$ ，有多解输出任意一个，无解输出 $−1$ 。

说白了还是在找$log$，我们发现如果有一个位置满足 $a_i-s_{i-1} \ge 0$，这样的位置不超过

$log$ 个，证明显然，所以直接大力维护 $a_i-s_{i-1}$ 然后判断区间 $max$ 是否大于$0$即可。再

来考虑怎么修改，我们可以考虑修改 $delta$ 而不是原值，所以在位置 $x$ 单点 $+delta$, $x$ 以

后的所有位置 $-delta$ 即可。

CF1000F One Occurence

给定一个长度为 $n$ 序列，$m$ 个询问，每次询问给定一个区间 $[l,r]$，如果这个区间里存在只出现一次的数，输出这个数（如果有多个就输出任意一个），没有就输出 $0$

直接莫队+分块莽！可以考虑值域分块，这样每一次的修改就变成 $O(1)$的了，查询的时候

照常做就行。

CF1149C Tree Generator™

给你一棵树的括号序列，输出它的直径。

有$m$次询问，每次询问表示交换两个括号，输出交换两个括号后的直径（保证每次操作后都为一棵树）

首先要观察出一个性质：括号序列上任何一个子区间，去掉所有匹配的括号后，得到的

括号序列一定是树上一条链，而且链的两端就是括号序列的两端！

去掉所有匹配的括号是复杂的，我们可以考虑确定性问题转$max,min$，也就是对于所

有子区间，找到一个分界点，右区间权值和 − 左区间权值和的最大值，为这个子区间

的路径长度最大值，其中钦定左括号是$+1$，右括号是$-1$，我们发现最后最优解一定是被

覆盖到的，而且不优解也会被排除掉。

CF1422F Boring Queries

区间求$LCM$，强制在线

$LCM$和$GCD$的关系是很大的，观察到如果一个区间里有大于$\sqrt n$的质因子，那么这个数

只要出现过我们就会乘上，相当于变成了存在性问题，那么对于小于$\sqrt n$的质因子，这样的

质因子有$87$个，可以直接拿$87$个$ST$表维护区间最大值。

对于存在性问题，可以考虑$HH$的项链，但是强制在线，这也很好处理，加上可持久化就可

以了，具体的我们维护一个 $root[i]$ 表示扫描线扫到 $i$ 的时候线段树的状况，那么我们在查

询区间$[l,r]$的时候自然就会想到，找到$root[r]$，然后查询这个版本的 $[l,r]$即可。

CF617E XOR and Favorite Number

给定一个长度为 $n$ 的序列 $a$，然后再给一个数字 $k$，再给出 $m$ 组询问，每组询问给出一个区间，求这个区间里面有多少个子区间的异或值为 $k$。

最初的想法是：对于每一个右端点找到对应的位置，然后再考虑二维数点，使用$KDtree$解决。但是如果所有数一

样，就会退化成$O(n^2)$。

考虑莫队，直接维护前缀异或和就好了，有三个细节要注意：

因为是$s[l-1]$和$s[r]$，所以初始读入的 $l$ 要减去 $1$
$pos[0]$要初始化为 $1$。
因为是异或，数组开大一点，至少到$1<<20$

[HNOI2016]大数

多次询问，不带修改，询问区间大数能整除$p$的个数

我们发现从后面添数是容易的，从前面添加是困难的。因为从前只需要找到$A=\frac{P-B}{10^i mod P}$。

$[L,R]×10^{n−R}=sum[L]−sum[R+1]$

$⇒[L,R]=\frac{sum[L]−sum[R+1]}{10^{n−R}}$

∴ $sum[L] mod P=sum[R+1] mod P$

然后就成了小$Z$的袜子

CF940F Machine Learning

查询区间 $[l,r]$ 中每个数字出现次数的 $mex$。

单点修改某一个位置的值。

考虑带修莫队，首先观察到一点，答案一定是小于$\sqrt n$的，于是先带修莫队，然后暴力扫描

$mex$就可以了。

注意带修改的莫队，要先按照 $l$ 所在块排序，再按 $r$ 所在的块排序，最后按照 $t$ 排序。时间

复杂度证明如下：

CF1787G Colorful Tree Again

定义一条路径为好，当且仅当：

1、所有边同色。

2、所有点均没有被锁。

3、包含了这种颜色的所有边。

定义一条路径的权值为边权之和。

现给定一棵树，有多次操作，每次锁或解锁一个点，你需要求出最大的好路径的权值，若不存在输出 $0$。

CF1783G Weighed Tree Radius

给定一棵 $n$ 个点，第 $i$ 个点有点权 $a_i$ 的树，对于一个点 $u$ 定义偏心距 $e(u)=max⁡$ {${dis(u,v)+a_v}$}，其中 $dis(u,v)$表示两点在树上的距离。定义半径 $r=min⁡$ $e_u$。

$m$ 次单点修改，每次修改后询问 $r$。

CF1774G Segment Covering

给定 $n$ 个区间 $[x_i,y_i]$，保证所有区间均不同。令 $f(l,r)$ 表示从 $n$ 个区间中选择偶数个区间使得其求并集后恰为 $[l,r]$ 的方案数，令 $g(l,r)$ 表示从 $n$ 个区间中选择奇数个区间使得其求并集后恰为 $[l,r]$ 的方案数。给定 $q$ 组询问 $[l_i,r_i]$，输出 $f(l_i,r_i)−g(l_i,r_i)$

首先挖掘性质：如果有两条线段 $X,Y$，其中 $X$ 包含了 $Y$ ，那么 $X$ 可以被删除，原因在于如果有方案选择了 $X$, 那么 $Y$ 的选择会对奇偶同时产生贡献。

然后我们考虑对于一个区间 $[l,r]$，我们把所有在这个区间内的线段提取出来，按照左端点排序，很容易发现第一条线段是必须选的，但是如果我们选择了三线段，那么二线段的有无又会同时产生贡献，于是三号线段是没有用的。

那么我们发现四号，五号....都被删除了，最后停在了某一号如图：

然后二号就变成了必选。

那么按照上面的方法删除线段后，只剩下了 $k$ 条必须选择的线段，答案就是$(-1)^k$

每次询问我们先找到左端点就是 $l$ 的线段和左端点大于 $l$ 且最小的两条线段作为起始线段。从他们开始，设他们编号 $1,2$，我们先从 $1$ 找到一个左端点大于 $r$ 且最小的线段 $3$，再对 $2$ 做，一直这么做下去，直到右端点到达 $r$。

那么我们按照上面这个步骤进行一个预处理：对于线段 $i$，我们找到最小的 $j$ 满足$l_j>r_i$，建一棵树（森林），我们令 $fa[i]=j$。事实上不用把树显式建出来，只要 $fa$ 数组就行。

这样我们每次先找到两条初始线段，只要线段范围没有超过 $r$，就一直倍增向后面跳 $fa$ ，如果最终两条线段的右端点还没到 $r$，或者最终两条线段是相同的，那么答案就是 $0$ 了。

CF1004F Sonya ans Bitwise OR

将 $a_i$ 修改成 $y$ ；

给定 $l$ 和 $r$ ，询问有多少个区间 $[L,R]$ 满足 $l≤L≤R≤r$ 且 $aL∼aR$ 按位或和至少为 $x$

这个题目给了我们全新的角度去观察 $or$ ，那就是：

前缀 $or$ 是单调不减的，所以可以分治双指针。
不同的前缀 $or$ 种类是不超过 $log$ 个的。

所以我们可以考虑对于线段树上每一个节点，记录前缀后缀$or$的种类和长度，这样的

位置至多只有 $log$ 个所以合并的时候可以考虑暴力合并。

CF1114F Please, another Queries on Array？

MULTIPLY l r x，对于所有 $i(l≤i≤r)$，将 $a_i$ 乘上 $x$。

TOTIENT l r，求出 $φ(∏_{i=l}^ra_i)$，

其中 $φ$ 表示欧拉函数，$φ(n)$ 的定义为 $1…n$ 中与 $n$ 互质的数的个数。

注意：欧拉函数虽然是积性函数，但不完全是：

若 $a , b$互质，则$ φ ( a b ) = φ ( a ) \times φ ( b ) $

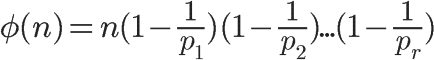
所以实际上我们只用维护有哪些质因子就可以了。

然后 $300$ 以内的质因子只有 $62$ 个，直接状压就可以了。

然后再维护一个区间乘积就可以了。

P4839 P哥的桶

维护一个集合序列，支持单点插入，区间查询最大异或和。

最大异或和？线性基！

那么就是普通的线性基插入，线性基合并了。

CF515E Drazil and Park

给定 $n$ 个点 $i$ 到点 $i+1$ 的距离 $d[i]$，每个点有一个权值 $h[i]$。现在有 $m$ 组询问，每次询问 $[l,r]$ 内两点 $x,y$，使得 $2×(hx+hy)+dis(x,y)$ 最大。其中 $dis(x,y)$ 表示 $x$ 到 $y$ 的距离。

考虑式子 $2\times h_x + 2\times h_y +dis(x,y)$。明显是要拆掉的。

第一步：拆掉$dis(x,y)$ $\rightarrow$ $sum[x]-sum[y]$

第二部：分离式子$\rightarrow$ $sum[x]+2\times h_x - (sum[y]-2\times h_y)$

那么很明显每一个点我们维护一个 $sum[i]+2\times h_i$，一个 $sum[i]-2\times h_i$

那么我们就在一个区间内找到一个最大的$A$式子，最小的$B$式子就可以了。

然后考虑如何处理$A，B$在一个点上的问题，那么我们就先删掉这个相同点，再找一遍最大最小值就可以了。

CF522D Closest Equals

现在有一个序列 $a_1,a_2,...,a_n$，还有 $m$ 个查询 $l_j,r_j (1≤l_j≤r_j≤n)$ 。对于每一个查询，请找出距离最近的两个元素 $a_x和 a_y(x≠y)$ ，并且满足以下条件：

$l_j≤x,y≤r_j$;

$a_x=a_y$

看到最近的两个元素，可以想到 $HH的项链$，具体怎么搞呢？

我们可以考虑把询问全部离线到右端点，然后假设我们当前扫描到了 $i$ ，我们就把 $pre[i]$的位置更新为 $i-pre[i]$ 一定注意是更新到 $pre[i]$ 而不是 $i$ ，画画图就能懂了。

那么询问就是区间最小值了。

P5386 [CNOI2019]数字游戏

给定一个排列，多次询问，求一个区间 $[l,r]$ 有多少个子区间的值都在区间 $[x,y]$ 内。

首先容易发现莫队是不好做的，但是我们可以考虑在值域上莫队，那么 $x,y$ 的限制就被我们消除了，剩下的是 $l,r$ 的问题了。

然后我们可以这样理解，我们现在序列上有一些 $1$，一段连续的 $1$ 的贡献是 $\frac {len\times (len-1)}{2}$，然后我们要求 $[l,r]$ 的贡献。

首先第一反应是线段树维护，但是这样会多一个 $log$ 显然过不去.......

那么我们考虑$O(1)$修改，$O(\sqrt n)$的查询，可以想到分块解决，但是要支持撤回。

具体的维护方法可以看代码

CF1771F Hossam and Range Minimum Query

给你一个长度为 $n$ 的非负整数序列 $a$。

有 $q$ 次询问，每次询问 $[l,r]$ 中满足出现次数为奇数的数当中，最小的那个是哪个数，不存在则输出 $0$

强制在线

考虑主席树，然后思考怎么快速判断一个区间内是否有出现次数为奇数的数。

异或 $HASH$ ，给每一个数字赋一个随机权值，那么有结论，一个区间如果存在出现次数为奇数的数，显然他异或值不为 $0$。

注意这里的主席树是值域上的，$root[i]$ 表示前缀异或 $[1,i]$ 的情况，查询的时候就查询$root[r]$ 和 $root[l-1]$ 即可。

int lval=tree[tree[p1].lc].val^tree[tree[p2].lc].val;

CF1767F Two Subtrees

给你一棵有根树，每次给出两个子树（可能有交），求这两个子树中所有的点权的最小众数。如果一个点被两个子树覆盖算两次。

区间众数是经典的不可以$polylog$的问题，通用解法是莫队或者摩尔投票。

$polylog:$$logn$，$log^2 n$，$log^3 n$。但$logn\times \sqrt n$不算

第一想法是把树拍平，然后跑莫队，但是这样会丢失树上的一些性质。

可以考虑$dsu$ $on$ $tree$ 的实现过程，轻子树暴力重子树保留，这给了我们很好的一个莫队顺序，

CF739C

现在有 $n$ 个数，$m$ 个操作，每次区间加一个数，对于每一次操作，你要找出最长的 $a_l...a_r$ ，满足

$∃k ⁣∈ ⁣[l,r],al<al+1<al+2<...<ak>ak+1>ak+2>...>ar$

输出其长度

要维护的东西是：

左右端点的值（$lval,rval$）。这是用于左右区间拼接时判断边界大小关系的。
以左端点开始的最长单减子段（$iseq$）。
以右端点结束的最长单增子段（$dseq$）。
以左端点开始的最长单峰子段（$lans$）。
以右端点结束的最长单峰子段（$rans$）。$2,3,4,5$ 都是用来拼接整个区间的单峰区间的。后面会详细讲到。
整个区间的最长单峰区间（$ans$）。
万年不变的懒标记（$tag$）。

~~有点ex~~

CF718C Sasha and Array

在本题中，我们用 $fi$ 来表示第 $i$ 个斐波那契数（$f1=f2=1,fi=fi−1+fi−2(i≥3)$）。

给定一个 $n$ 个数的序列 $a$。有 $m$ 次操作，操作有两种：

将 $al∼ar$ 加上 $x$。

求$ (∑_{i=l}^{r}f_{a_i}) mod (1e9+7)$。

由于是斐波那契所以想到矩阵维护一下，然后矩阵有一个性质：

$a\times b+a\times c=a\times (b+c)$

所以区间加，就变成了区间乘矩阵了。

CF803G Periodic RMQ Problem

给你一个序列aa 让你支持

$1\quad l，r，x$ 区间赋值

$2\quad l，r$ 询问区间最小值

我们觉得这个问题太水了,所以我们不会给你序列 $a$

而是给你序列一个长度为 $n$ 的序列 $b$ ,把 $b$ 复制粘贴 $k$ 次就可以得到 $a$

~~似曾相识~~

直接动态开点权值线段树就可以了，然后利用$ST$表进行新建点的时候的初始化。

CF911G Mass Change Queries

给出一个数列,有$q$个操作,每种操作是把区间$[l,r]$中等于$x$的数改成$y$.输出$q$步操作完的数列.

因为值域只有$100$，所以可以建立$100$ 棵线段树出来，那么某个值在一个区间里有值，当且仅当这棵线段树在这个区间里有点。

那么在把$x$ 变为 $y$ 的时候，就相当于是把 $x$ 的线段树在这个区间里的点移动到线段树
$y$ 上面去，也就是线段树合并。

void modify(int& a,int& b,int l,int r,int x,int y){
	if(!a)return ;
	if(l > y or r < x)return ;
	if(l >= x and r <= y) {
		b = merge(a , b);
        a = 0;
		return;
	}
	if(!b)
		b = ++cnt;
	int mid = (l + r) >> 1;
	modify(lson[a],lson[b],l,mid,x,y);
	modify(rson[a],rson[b],mid+1,r,x,y);
}

P4062 Yazid的新生舞会

求有多少个子区间内的众数在该子区间的出现次数严格大于 $\frac{r−l+1}{2}$

区间众数，无法$polylog$.....吗？注意这里的众数是绝对众数！

~~经典题~~

所以我们考虑枚举众数，然后考虑怎么计算他的贡献，我们发现，如果把是该数的位置赋值为$1$，不是该数的位置赋值为 $0$，那么$l,r$ 能成为众数的条件就是 $S_r-S_l>r-l-(S_r-S_l)$。拆掉式子就是$2S_r-r>2S_l-l$，那么问题变成了求全局顺序对个数。

如果我们每一次都是$O(nlogn)$的去做这个东西，显然不可行，于是考虑找性质。

我们发现对于前缀和数组$S$，一定是被拆成了一段一段等差数列的，例如：

$0,-1,-2/-1,-2,-3/-2,-3/-2/-1,-2$

可以发现在同一段里面是没有贡献的，而且这样的关键点加起来是$O(n)$的，是非常好的性质。

记 $T_i$ 表示权值的前缀和，即 $T_i=∑_{j=1}^i c_i$。对段内每个位置的 $P_i$ ，我们得到的贡献是 $T_{P_i−1}$。也就是说，对整个段内 $[x,y]$ 这些数，总贡献是 $∑_{i=x−1}^{y−1}Ti$。记 $G_i$ 表示权值的前缀和的前缀和，即 $G_i=∑_{j=1}^{i}T_j$，那么总贡献可以表示为 $G_{y−1}−G_{x−1}$。

那么问题就变成了区间加法，区间求二阶前缀和。

可以考虑线段树维护权值的前缀和 $T_i$ ，这样在 $[x,y]$ 上的区间加 $1$ 就变成了：在 $[x,y]$ 上加等差数列 $1,2,3,…,y−x+1$，在 $[y+1,2n+1]$ 上加上 $y−x+1$。后者也可看成是公差为 $0$ 的等差数列。

然后区间求和就做完了。

P4314 CPU监控

区间加，区间赋值，区间最大值，区间历史最大值。

吉司机线段树？

~~其实不用太麻烦~~

这里首先有一个技巧，就是说如果有区间加和区间赋值操作，那么在第一次的区间赋值操作之后，后面所有的区间加操作都可以视作区间赋值操作。

这样，一个区间的操作序列就被劈成了两半，一半全是区间加，另一半全是区间赋值。

那么怎么维护区间历史最大值呢？我们先考虑左半边，那么我们可以维护一个上次下放之后的最大加和，上次下方之后的最大赋值，在此之前先维护一个“是否进行过区间赋值的$tag$"，假如我们当前有一个区间加，就先看$vis$是否为$1$，是就直接更新最大赋值，否就更新最大加和，区间赋值也是同理。

更详细的可以看这里

CF840D Destiny

给定 $n$ 个元素，$m$ 次询问。

每次给出三个参数 $l,r,k$，询问区间 $[l,r]$ 内是否存在出现次数严格大于$\frac{r−l+1}{k}$ 的数。如果存在就输出最小的那个 $ans$，否则输出 $-1$.

建立主席树，然后两个版本相减，然后递归左右子树，如果总次数超过目标说明很有可能这个子区间存在答案，当然会出现实际不存在的情况，但是最多只会有$k$次这种情况。如图：

CF817F Mex Queries

将 l 到 r 的区间用 1 覆盖

将 l 到 r 的区间用 0 覆盖

将 l 到 r 的区间取反

区间的初始值都为 0。

在每次操作后输出第一个 0 的下标。

虽然用动态开点线段树和线段树上二分也可以做，但是我们还是要学习珂朵莉树。

struct node{
    int l,r;
	mutable int val;//区间端点、权值
    bool operator<(const node &t) const{
		return l<t.l;
	}

};
int n;
set<node> s;
se it,itl,itr;
inline se split(int pos){
    it=s.lower_bound(node({pos}));
    if(it!=s.end()&&it->l==pos)
		return it;
    --it;
    int l=it->l,r=it->r,v=it->val;
    s.erase(it);
    s.insert(node({l,pos-1,v}));
    return s.insert(node({pos,r,v})).first;
}//分裂成 2 个区间
inline void assign(int l,int r,int val){
    itr=split(r+1),itl=split(l);
    //这里特别注意顺序不要颠倒了！
    s.erase(itl,itr);
    s.insert(node({l,r,val}));
}//区间覆盖
inline void rever(int l,int r){
    itr=split(r+1),itl=split(l);
    for(se it=itl;it!=itr;++it)
        it->val=!it->val;
}//区间取反

CF1725E Electrical Efficiency

树上 $n$ 个点，每个点有点权 $a_i$。对于一个三元组 $(x,y,z)$ 满足$ 1≤x<y<z≤n$，定义 $f(x,y,z)$ 为树上连通这三个点的连通块的最小边数（即三个点两两间路径的并的边数），$g(x,y,z)$为 $gcd⁡(a_x,a_y,a_z)$ 所含的不同质因子个数，求 $∑f(x,y,z)×g(x,y,z)$

原答案等价于$∑_{d∈P}∑f(x,y,z)[d∣gcd(a_x,a_y,a_z)]$。
$f(x,y,z)=\frac{dis(x,y)+dis(x,z)+dis(y,z)}{2}$

所以$∑f(x,y,z)=\frac{(n−2)}{2}∑dis(x,y)$。

然后枚举质数 $p$，把所有 $p∣a_i$ 的点拎出来建虚树，然后一次 $dfs$ 算出任意两点间的距离之和（注意只计算关键点的贡献，对于保持树的形态加入的点不算）。

左偏树：

int find(int x){return rt[x]==x?x:rt[x]=find(rt[x]);}
int merge(int x,int y)
{
 if(!x||!y)return x+y;
 if(v[y]<v[x])swap(x,y);
 rc[x]=merge(rc[x],y);
 if(dist[lc[x]]<dist[rc[x]])swap(lc[x],rc[x]);
 dist[x]=dist[rc[x]]+1;
 return x;
}

P3224 永无乡

B x y 表示在岛 $x$ 与岛 $y$ 之间修建一座新桥。

Q x k 表示询问当前所与岛 $x$ 连通的岛中重要度排名第 $k$ 小的岛是哪座，请你输出那个岛的编号。

可以考虑并查集和线段树合并，具体来说，每一个连通块在 $rt$ 处都会有一个线段树，那么合并两个连通块就变成了合并两棵线段树，查询就是查询第 $k$ 大。

P3521 POT-Tree Rotation

给定一颗有 $n$ 个叶节点的二叉树。每个叶节点都有一个权值 $p_i$（注意，根不是叶节点），所有叶节点的权值构成了一个 $1∼n$ 的排列。
对于这棵二叉树的任何一个结点，保证其要么是叶节点，要么左右两个孩子都存在。
现在你可以任选一些节点，交换这些节点的左右子树。
在最终的树上，按照先序遍历遍历整棵树并依次写下遇到的叶结点的权值构成一个长度为 $n$ 的排列，你需要最小化这个排列的逆序对数。

一定要注意！每个节点交不交换都是互不影响的！这就说明我们每个点能换就要换，不能换就不换！

那么问题就变成怎么快速求逆序对了。

这个题的解决方法和分治求逆序对是很像的，我们可以考虑线段树合并，那么：

用 $p$ 表示左子树，$q$ 表示右子树。$ls$ 表示左子节点，$rs$ 表示右子节点。

很明显，对于除了叶节点的每一个节点：

如果不交换： $u+=[p.rs].size∗[q.ls].size$
如果交换： $v+=[p.ls].size∗[q.rs].size$

这里的节点是指值域线段树上的节点。

P2824 [HEOI2016/TJOI2016]排序

0 l r 表示将区间 $[l,r]$ 的数字升序排序

1 l r 表示将区间 $[l,r]$ 的数字降序排序

注意，这里是对下标在区间 $[l,r]$ 内的数排序。
最后询问第 $q$ 位置上的数字。

因为只会询问一个位置，所以可以二分答案，那么问题就变成了区间赋$0,1$值区间求和了。

如果查询的位置是$1$，就$l=mid+1$，否则$r=mid-1$

当然因为是区间推平和区间求和，也可以$ODT$

CF558E A Simple Task

给定一个长度不超过$1e5$的字符串，每次给定区间，要求区间升序降序排序

很经典的一道题目，考虑建树，每个点维护$26$个字母在当前区间的个数，那么排序的时候相当于是先区间求出数组，然后再区间赋值即可。

P3437 [POI2006]TET-Tetris 3D

二维区间赋值，一次整体最值。

看一看数据范围，显然的二维线段树。

那么我们考虑怎么维护，我们发现如果方块掉落在了一片参差不齐的位置，那么我们最后一定是将这一片区间先找到最值，然后区间赋值为最大值$+k$。

当然需要标记永久化一下。

P5524 [Ynoi2012]NOIP2015充满了希望

给一个长为 $n$ 的序列，有 $m$ 个操作，操作编号从 $1$ 到 $m$，每个操作为：

1 x y：将序列位置为 $x,y$ 的两个元素交换。

2 l r x：将序列区间 $[l,r]$ 内所有元素修改为 $x$。

3 x：查询序列 $x$ 位置的值。

现在有 $q$ 次查询，每次查询给出一个操作的区间 $[l,r]$：

先将序列中的元素全部置为 $0$，之后依次进行从 $l$ 到 $r$ 的所有操作，求出所有这些操作中所有 $3$ 操作的答案的和。

查询之间独立。

看到这种区间推平，就容易想到对于每一个位置都找到最后一个影响到它的操作的位置。

那么我们对于所有的 $3$ 操作都找到影响到他的最前面的操作，假设为$pos$，那么在询问的时候如果 $l$ 在 $pos$ 右边，那么当前位置是没有值的。

那么现在问题就变成了，每一个位置有一个 $pos$ 值一个 $val$值，$q$次询问，每次询问在$l,r$中，$pos_i$大于 $l$ 的 $val_i$ 的和。

直接树状数组就可以了。

P4168 [Violet]蒲公英

区间众数，强制在线

$n\le40000$，$m\le 50000$ ，$w\le 10^9$

可以考虑预处理两个数组：

$p[i][j]$表示块 $i$ 到块 $j$ 的最小众数是谁。

$s[i][j]$表示前$i$个块中数 $j$ 出现的次数。

有这两个数组就可以处理了

P5048 [Ynoi2019] Yuno loves sqrt technology III

区间众数，强制在线

$n\le500000$，$m\le 500000$ ，$w\le 10^9$

数据范围太大了，显然我们的$s[i][j]$开不下了，那么我们还是预处理出$p[i][j]$数组，然后考虑散块怎么处理。

我们可以这样考虑，我们先使用$n$个$vector[i]$记录数$i$出现的位置集合。

然后记$p_i$表示$i$这位上的数在$vector[a_i]$是第几个，然后在询问的时候还是先把$s[bl+1][br-1]$找出来，再考虑散块是否会成为众数，设$s[bl+1][br-1]=T$，注意$T$是出现次数，那么散块想要成为众数，必须出现大于$T$次，也就是说，出现第$T+now$次的数要在$l,r$范围内。

P1712 [NOI2016] 区间

在数轴上有 $n$ 个闭区间从 $1$ 至 $n$ 编号，第 $i$ 个闭区间为 $[l_i,r_i]$ 。

现在要从中选出 $m$ 个区间，使得这 $m$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$ ，使得对于每一个被选中的区间 $[l_i,r_i]$，都有 $l_i≤x≤r_i$ 。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。

区间 $[l_i,r_i]$ 的长度定义为 $(r_i−l_i)$ ，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 $−1$。

双指针，左端点固定时，右端点移动，如果有一个点被覆盖了超过$k$次就停止。

固定右端点也是可以的，那么就变成了

for (int i = 1; i <= n; i++) {
	sgt.modify(1, 1, tot, a[i].l, a[i].r, 1);
	while (sgt.query_all() >= m) {
		chkmin(ret, a[i].length - a[tmpl].length);
		sgt.modify(1, 1, tot, a[tmpl].l, a[tmpl].r, -1);
		tmpl++;
	}
}

P3793 由乃与大母神原型和偶像崇拜

给你一个长为 $n$ 的序列 $a$

每次两个操作：

修改 $x$ 位置的值为 $y$

查询区间 $[l,r]$ 是否可以重排为值域上连续的一段

这个题很神奇，我们发现这个东西很难维护，于是考虑有没有什么正确率高一些的维护方法。

那么我们可以维护线段树区间最小值，区间最大值和区间平方和。

这里补一个连续平方和公式：

\[1^2+2^2+...+n^2 \\\\ =1\times(2-1)+2\times(3-1)+...+n\times(n+1-1) \]

因为$n\times(n+1)=\frac{1}{3}[n(n+1)(n+2)-(n-1)n(n+1)]$

\[S=\frac{1}{3}[1\times2\times3-0\times1\times2]+\frac{1}{3}[2\times3\times4-1\times2\times3]+... \]

\[=\frac{1}{3}[n(n+1)(n+2)]-\frac{n(n+1)}{2} \\\\ =\frac{n\times(n+1)\times(2n+1)}{6} \]

P2633 Count on a tree

给定一棵树，每次询问一条路径上标号第 $k$ 小的点是谁

可以考虑可持久化线段树，我们设在节点 $i$ 的主席树是 $s[i]$，那么答案就是：

\[s[u]+s[v]−s[lca(u,v)]−s[fa[lca(u,v)]] \]

的主席树的树。

然后我们没有必要真的一个一个加减把最后得到的树求出来，我们只需要在多个树上同时向左向右走就可以了（有点类似树套树的方法，参见$dynamic$ $ranking$

inline int query(Node x, Node y, Node z, Node w, int l, int r, int k) {
    if (l == r) return l;
    int sum = node[x.l].sum + node[y.l].sum - node[z.l].sum - node[w.l].sum;
    int mid = (l + r) >> 1;
    if(sum >= k) return query(node[x.l], node[y.l], node[z.l], node[w.l], l, mid, k);
    return query(node[x.r], node[y.r], node[z.r], node[w.r], mid+1, r, k - sum);
}

P2839 middle

回答 $Q$ 个这样的询问：$s$ 的左端点在 $[a,b]$ 之间，右端点在 $[c,d]$ 之间的子区间中，最大的中位数。

看到区间中位数，一定要反应过来是枚举$mid$，然后大于等于 $mid$ 的赋值为 $1$，否则赋值为 $-1$，判断就直接判断和是否大于 $0$ 就可以了。

但是我们有多次 $check$，所以要开一个主席树，$rt[i]$表示当前 $mid=i$ 的时候数组内 $-1$和$1$的情况是什么样子的。

然后$check$就是前区间$rmax$ + 后区间$lmax +$ 必选区间$$[b + 1, c - 1]$$是否$>=0$

P4577 [FJOI2018] 领导集团问题

给定一棵树，求$求 ∣Smax∣使得 ∀i,j(ancestor of i)∈S,wi≤wj$

可以设$dp[u][x]$表示点 $u$ 的子树中，大于$x$ 选的节点全都大于 $x$ 的最大子集大小

那么转移就是：

$x∈[1,n],f(u,x)=∑_{v是u的儿子节点}f(v,x)$

$x∈[1,w_u],f(u,x)max⁡=∑_{v在u的儿子节点}f(v,w_u)+1$

每个点用线段树维护第二维度。

那么问题就变成了区间对一个数取$max$（推平），区间加。

维护方式就是同时记录区间加和区间取$max$，像这样：

void seg_add(int x,int v)
{
    t[x].sum+=v;
    if(t[x].assign!=-1)
    	t[x].assign+=v;
    t[x].add+=v;
}
void assign(int x,int v)
{
   t[x].sum=max(t[x].sum,v);
   t[x].assign=max(v,t[x].assign);
}
void pushdown(int k)
{
	if(!t[k].lson) t[k].lson=getnode();
	if(!t[k].rson) t[k].rson=getnode();
	if (t[k].add)
	{
	    t[t[k].lson].sum+=t[k].add;
	    t[t[k].rson].sum+=t[k].add;
	    t[t[k].lson].add+=t[k].add;
	    t[t[k].rson].add+=t[k].add;
	    t[t[k].lson].assign+=t[k].add;
	    t[t[k].rson].assign+=t[k].add;
	    t[k].add=0;
	} 
	if (t[k].assign != -1)
	{
	    t[t[k].lson].sum=max(t[k].assign,t[t[k].lson].sum);
	    t[t[k].rson].sum=max(t[k].assign,t[t[k].rson].sum);
	    t[t[k].lson].assign=max(t[k].assign,t[t[k].lson].assign);
	    t[t[k].rson].assign=max(t[k].assign,t[t[k].rson].assign);
	    t[k].assign=-1;
	}
	
}

他的原理是这样的：

![null (3)](E:\3_disk_c\DS\pics\null (3).png)

P4331 Sequence 数字序列

给定一个整数序列 $a1,a2,⋅⋅⋅,an$ 求出一个递增序列 $b1<b2<⋅⋅⋅<bn$，使得序列$a_i$和 $b_i$ 的各项之差的绝对值之和$∣a1−b1∣+∣a2−b2∣+⋅⋅⋅+∣an−bn∣$ 最小。

①：若原序列a满足 $a1<a2<…<an$，显然最优情况为 $b_i=a_i$

②：若原序列a满足 $a1>a2>…>an$，显然最优情况为 $b_{mid}=x$（$x$为$a$中位数）

有了上述的两种情况，不难发现，整个 $a$ 序列是尤一些单调区间组成。

所以我们可以将原序列a拆成若干个单调区间，最后再将答案合并。

我们可以重新找一个中位数来合并。

假设我们已经找到前 $k$ 个数的最优解，队列中有 $cnt$ 段区间，每段区间最优解为$w1,w2,…,wcnt$，现在要加入 $a_{k+1}$，并更新队列。

首先把 $ak+1$ 加入队尾，令 $w_{cnt+1}=a_{k+1}$ 如果 $w_{cnt}>w_{cnt+1}$，就将最后两个区间合并，并找出新区间的最优解。重复上述过程，直至满足 $w$ 单调递增。

P3732 供给侧改革

Anihc 国提高社会生产力水平，落实好以人民为中心的发展思想，决定进行供给侧结构性改革。

为了提高供给品质，你调查了某个产业近来 $n$ 个时期的供求关系平衡情况，每个时期的情况都用 $0$ 或 $1$ 中的一个数字来表示。于是这就是—个长度为 $n$ 的 $\texttt{01}$ 字符串 $S$。为了更好的了解这一些数据，你需要解决一些询问，我们令 $\text{data}(L,R)$ 表示：在字符串 $S$ 中，起始位置在 $[L,R]$ 之间的这些后缀之中，具有最长公共前缀的两个后缀的最长公共前缀的长度。

对于每一个询问 $L,R$，求：

\[ans = \sum_{L \leqslant i < R} \text{data}(i,R) \]
由于你其实根本没有时间调查，所以这些数据都是乱编的，即串 $S$ 中的每一位都是在 $0$ 和 $1$ 之间随机产生的。