前置知识:动态开点权值线段树。
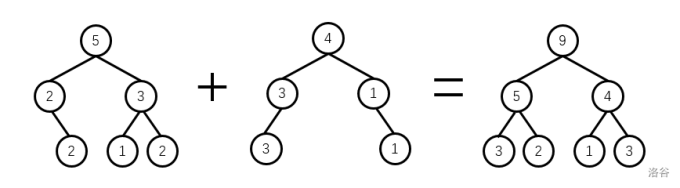
线段树合并,顾名思义,就是将两棵权值线段树合并在一起。为什么不把两棵普通的线段树合并呢?因为那样好像没啥用。
我们知道,权值线段树支持着查询某个数的个数、查询第 \(k\) 大/小的数等操作,有了合并操作之后就可能会支持一些令人意想不到的操作。
放张图,可以帮助理解下。
1 实现方式
线段树合并的代码其实非常简单,这里先直接贴上来:
int merge(int x,int y,int l,int r){ //y合并到x上
if(!x||!y) return x|y; //x和y有一个为空
if(l==r){
//do something to merge...
return x;
}
int mid=(l+r)>>1;
ls[x]=merge(ls[x],ls[y],l,mid); //左右儿子继续合并
rs[x]=merge(rs[x],rs[y],mid+1,r);
pushup(x);
return x;
}
是不是十分甚至九分的好理解?不再具体展开讲了。
唯一要注意的就是,把 \(y\) 合并到 \(x\) 上之后,如果今后又把 \(x\) 合并到了其它树上很可能会把 \(y\) 的结构破坏掉,因此合并到其他树上的线段树要保证今后不再使用。
当然也是有解决方法的,对于都有的结点直接选择新开一个结点而非使用 \(y\) 的结点,但是空间复杂度爆炸。
2 时间复杂度
先谈时间上,根据上面的代码,显然有一点:两棵线段树合并复杂度只取于它们在值域上重合的点数,因此总复杂度一定不会超过点数。
设有 \(m\) 次单点修改操作,合并 \(n\) 棵线段树,动态开点每次最多增加 \(O(\log n)\) 个结点,因此总结点数是 \(O(m\log n)\) 的,时间复杂度不会超过 \(O(m\log n)\)。
空间复杂度由于是动态开点,与时间复杂度一致,同为 \(O(m\log n)\)。
总体上看复杂度还是非常优秀的,当然具体实现的时候多少会带个两倍左右常数,还是记得空间之类的放大点。
3 例题
洛谷 P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并
题意:\(n\) 个房子连成一棵树,\(m\) 次操作,每次给 \((x,y)\) 路径上的房子发一袋 \(z\) 类型救济粮,问所有操作结束后每座房子数量最多的救济粮的类型。
分析:对于每个结点,考虑分别开一棵权值线段树维护每种救济粮的数量和最多的救济粮的类型。
由于是路径加,且是所有修改结束之后再进行询问,因此直接考虑树上差分。最后的时候直接把所有权值线段树自下而上合并即可。
代码其实挺短的,时空复杂度 \(O(m\log n)\)。
const int N=5e5+5;
struct Edge{
int nxt,to;
}e[N];
int n,m,cnt,head[N];
int siz[N],son[N],dep[N],fa[N],top[N];
int tot,sum[N*20],maxp[N*20],ls[N*20],rs[N*20],rt[N],ans[N];
void add_edge(int u,int v){
e[++cnt]={head[u],v};
head[u]=cnt;
}
void dfs1(int now,int fath){
dep[now]=dep[fath]+1;siz[now]=1;fa[now]=fath;
for(int i=head[now];i;i=e[i].nxt){
int to=e[i].to;
if(to==fath) continue;
dfs1(to,now);siz[now]+=siz[to];
if(siz[to]>siz[son[now]]) son[now]=to;
}
}
void dfs2(int now,int lmt){
top[now]=lmt;
if(!son[now]) return;
dfs2(son[now],lmt);
for(int i=head[now];i;i=e[i].nxt){
int to=e[i].to;
if(top[to]) continue;
dfs2(to,to);
}
}
int LCA(int x,int y){ //常规的树剖求LCA,不喜欢倍增
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
void pushup(int k){
if(sum[ls[k]]>=sum[rs[k]]) sum[k]=sum[ls[k]],maxp[k]=maxp[ls[k]];
else sum[k]=sum[rs[k]],maxp[k]=maxp[rs[k]];
}
int modify(int x,int y,int l,int r,int k){ //权值线段树单点修改
if(!k) k=++tot;
if(l==r){sum[k]+=y,maxp[k]=x;return k;}
int mid=(l+r)>>1;
if(x<=mid) ls[k]=modify(x,y,l,mid,ls[k]);
else rs[k]=modify(x,y,mid+1,r,rs[k]);
pushup(k);return k;
}
int merge(int x,int y,int l,int r){ //线段树合并
if(!x||!y) return x|y;
if(l==r) return sum[x]+=sum[y],x;
int mid=(l+r)>>1;
ls[x]=merge(ls[x],ls[y],l,mid);
rs[x]=merge(rs[x],rs[y],mid+1,r);
pushup(x);
return x;
}
void get_ans(int now){
for(int i=head[now];i;i=e[i].nxt){
int to=e[i].to;
if(to==fa[now]) continue;
get_ans(to); //先搞完子树,再统计自己
rt[now]=merge(rt[now],rt[to],1,1e5);
}
ans[now]=sum[rt[now]]>0?maxp[rt[now]]:0; //别忘了特判没有粮食
}
void Main(){
read(n,m);
For(i,1,n-1){
int u=read(),v=read();
add_edge(u,v);add_edge(v,u);
}
dfs1(1,0);dfs2(1,1);
For(i,1,m){
int x=read(),y=read(),z=read(),lca=LCA(x,y);
rt[x]=modify(z,1,1,1e5,rt[x]); //常规树上差分
rt[y]=modify(z,1,1,1e5,rt[y]);
rt[lca]=modify(z,-1,1,1e5,rt[lca]);
rt[fa[lca]]=modify(z,-1,1,1e5,rt[fa[lca]]);
}
get_ans(1);
For(i,1,n) printf("%d\n",ans[i]);
}
洛谷 P3224 [HNOI2012]永无乡
题意:有 \(n\) 个点和 \(q\) 次操作,每个点有一个权值,且保证 \(n\) 个点的权值形成一个从 \(1\) 到 \(n\) 的排列,初始时每个点各自为一个集合。要求支持的操作如下:
-
将点 \(x\) 和点 \(y\) 所在的集合合并为同一个集合。
-
求点 \(x\) 所在集合的所有点中权值第 \(k\) 小的点。
分析:涉及到集合的合并与整体第 \(k\) 小,很容易想到线段树合并。
考虑直接对 \(n\) 个点各自开一个权值线段树维护权值出现次数和每个权值对应的点,对于操作一显然直接合并即可维护。
对于操作二,我们目前的问题就是在操作一合并之后,如何找到 \(x\) 所在集合中最后合并到的那棵线段树,因为前文说过如果一棵线段树之前被合并到了另一棵上,它的结构很有可能会被破坏掉。实际上也非常简单,我们直接在合并的时候顺便维护一个并查集就可以解决了。
要注意的一点是并查集的合并方向一定要与线段树合并的方向一致,即如果线段树合并的顺序是 \(y\) 合并到 \(x\) 上,那么并查集中也一定是要把 \(y\) 合并到 \(x\) 上。
时空复杂度均为 \(O(q\log n)\)。
int n,m,q,p[N],fa[N];
int cnt_node,rt[N],sum[N<<5],id[N<<5],ch[N<<5][2];
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void modify(int x,int idx,int l,int r,int &now){
if(!now) now=++cnt_node;
if(l==r){
sum[now]++;id[now]=idx;
return;
}
int mid=(l+r)>>1;
if(x<=mid) modify(x,idx,l,mid,ls(now));
else modify(x,idx,mid+1,r,rs(now));
sum[now]=sum[ls(now)]+sum[rs(now)];
}
int merge(int x,int y,int l,int r){
if(!x||!y) return x|y;
if(l==r){
if(id[y]) id[x]=id[y],sum[x]+=sum[y];
return x;
}
int mid=(l+r)>>1;
ls(x)=merge(ls(x),ls(y),l,mid);
rs(x)=merge(rs(x),rs(y),mid+1,r);
sum[x]=sum[ls(x)]+sum[rs(x)];
return x;
}
int queryKth(int k,int l,int r,int now){
if(sum[now]<k) return 0;
if(l==r) return id[now];
int mid=(l+r)>>1;
if(k<=sum[ls(now)]) return queryKth(k,l,mid,ls(now));
else return queryKth(k-sum[ls(now)],mid+1,r,rs(now));
}
void Main(){
read(n,m);
For(i,1,n){
read(p[i]);fa[i]=i;
modify(p[i],i,1,n,rt[i]);
}
For(i,1,m){
int x=read(),y=read();
int fx=find(x),fy=find(y);
if(fx==fy) continue;
fa[fy]=fx;merge(rt[fx],rt[fy],1,n);
}
char opt;read(q);
while(q--){
cin>>opt;
if(opt=='B'){
int x=read(),y=read();
int fx=find(x),fy=find(y);
if(fx==fy) continue;
fa[fy]=fx;rt[fx]=merge(rt[fx],rt[fy],1,n);
}
else{
int x=read(),k=read(),fx=find(x);
int ans=queryKth(k,1,n,rt[fx]);
printf("%d\n",!ans?-1:ans);
}
}
}