526互联

线段树优化建图

发布时间 2023-12-07 11:43:11作者: 小超手123

线段树优化建图学习笔记

CF786B Legacy

题意：

有 n 个点、q 次操作。每一种操作为以下三种类型中的一种：

  • 操作一：连一条 u 到 v 的有向边，权值为 w。

  • 操作二：连一条 u 到 [l,r] 的有向边，权值为 w。

  • 操作三：连一条 [l,r] 到 u 的有向边，权值为 w。

求从点 s 到其他点的最短路。

前言：

图片懒得画，用的 maoyiting 大佬的图。

分析：

直接建图边的数量级是 nq 的，需要减少边的数量。

由于 [l,r] 是一段连续的区间，不妨考虑利用线段树优化建图。

操作 1 被操作 2 包含，故这里只考虑操作 2,3。

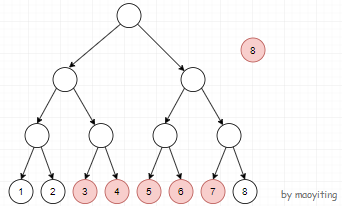
先考虑询问 2，这里对编号为 8 的点连一条到 [3,7] 的点，对该区间利用线段树拆成 [3,4],[5,6],[7,7] 这三个区间。那么只需要从 8 连一条到这三个区间所表示的节点即可。 但要从区间落实点怎么办呢？对一个节点分别连一条到 TA 左右儿子的边权为 0 的边即可。

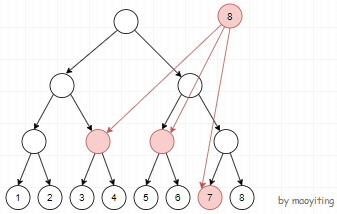
询问 3 类似，不过是内向边。

如何组合起来呢？

我们建两棵线段树。

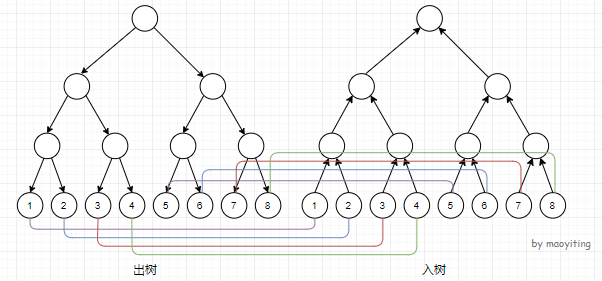
image.png

首先将处于同一位置的两个叶子节点连一条边权为 0 的边。

image.png

对于操作 2，从入树的叶子节点连一条到出树的对应区间节点的边。

对于操作 3，从入树的对于区间节点连一条到出树的叶子节点的边。

这样边的数量被优化到 q \log n。

然后跑 dijstra 就做完了。

代码：
#include<bits/stdc++.h>
#define int long long
#define N 100005 
#define K 2000000
using namespace std; 
int read() {
    char ch = getchar(); int x = 0, f = 1;
    while(ch < '0' || ch > '9') if(ch == '-') f = -1, ch = getchar();
    while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}
void write(int x) {
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) write(x / 10);
    putchar('0' + x % 10);
}
int n, q, s, opt, Max;
int h[N], dis[N * 40]; //h[i]表示i这个位置在线段树上的编号 
struct edge {int to, w; };
vector<edge>p[N * 40];
bool vis[N * 40];
void add(int u, int v, int w) { p[u].push_back((edge){v, w}); }
void build(int u, int L, int R) {
    if(L == R) {
        h[L] = u;
        Max = max(Max, u);
        return;
    }
    add(u, u * 2, 0); add(u, u * 2 + 1, 0); //在外向树上连边 
    add(u * 2 + K, u + K, 0); add(u * 2 + 1 + K, u + K, 0);  //在内向树上连边 
    int mid = (L + R) / 2;
    build(u * 2, L, mid); build(u * 2 + 1, mid + 1, R);
}
void update(int u, int L, int R, int l, int r, int x, int w) {
    if(r < L || R < l) return;
    if(l <= L && R <= r) {
        if(opt == 2) add(h[x] + K, u, w);
        else add(u + K, h[x], w);
        return;
    }
    int mid = (L + R) / 2;
    update(u * 2, L, mid, l, r, x, w);
    update(u * 2 + 1, mid + 1, R, l, r, x, w);
}
struct node{
    int v, w;
    friend bool operator < (node x, node y) {
        return x.w > y.w;
    }
};
priority_queue<node>Q;
void Dijstra() {
    Max += K;
    for(int i = 1; i <= Max; i++) dis[i] = 1e18;
    dis[h[s]] = 0;
    Q.push((node){h[s], 0});
    while(!Q.empty()) {
        int x = Q.top().v;
        Q.pop(); 
        if(vis[x]) continue;
        vis[x] = 1;
        for(int i = 0; i < p[x].size(); i++) {
            int y = p[x][i].to;
if(dis[y] > dis[x] + p[x][i].w) {
dis[y] = dis[x] + p[x][i].w;
Q.push((node){y, dis[y]});
    }
    }
    }
}
signed main() {
n = read(), q = read(), s = read();
    build(1, 1, n);
    for(int i = 1; i <= n; i++) add(h[i], h[i] + K, 0), add(h[i] + K, h[i], 0); //叶子结点间互相连边
for(int i = 1, v, u, l, r, w; i <= q; i++) {
opt = read();
if(opt == 1) {
v = read(), u = read(), w = read();
add(h[v] + K, h[u], w);
    }
else {
v = read(), l = read(), r = read(), w = read();
update(1, 1, n, l, r, v, w);
    }
    }
Dijstra();
for(int i = 1; i <= n; i++) printf("%lld ", dis[h[i]] == 1e18 ? -1 : dis[h[i]]);
return 0;
}
​

P5025 [SNOI2017] 炸弹

题意：

在一条直线上有 n 个炸弹，每个炸弹的坐标是 x_i ，爆炸半径是 r_i ，当一个炸弹爆炸时，如果另一个炸弹所在位置 x_j 满足： |x_j-x_i| \le r_i ，那么，该炸弹也会被引爆。 现在，请你帮忙计算一下，先把第 i 个炸弹引爆，将引爆多少个炸弹呢？

答案对 10^9 + 7 取模

分析：

求每个点用二分求出 TA 能直接引爆的最远左右端点。

然后利用线段树把图建出来。再用 tarjan 缩点。

对每个强连通分量，我们记 gl[i],gr[i] 分别表示该强连通分量的所有点所表示的区间中的最小点，最大点。

在 DAG 上拓扑排序一下就做完了。

代码：
#include<bits/stdc++.h>
#define int long long
#define N 2000006
#define mod 1000000007
using namespace std;
bool P1;
int read() {
    char ch = getchar(); int x = 0, f = 1;
    while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
    while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}
void write(int x) {
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) write(x / 10);
    putchar('0' + x % 10);
}
int n, P;
int x[N], r[N], h[N], ll[N], rr[N];
vector<int>p[N], G[N];
unordered_map<int, unordered_map<int, int>>vis;
void add(int u, int v) {p[u].push_back(v); }
void build(int u, int L, int R) {
    ll[u] = L, rr[u] = R;
    if(L == R) {
        h[L] = u;
        P = max(P, u);
        return;
    }
    add(u, u * 2);
    add(u, u * 2 + 1);
    int mid = (L + R) / 2;
    build(u * 2, L, mid);
    build(u * 2 + 1, mid + 1, R);
}
void update(int u, int L, int R, int l, int r, int x) {
    if(r < L || R < l) return;
    if(l <= L && R <= r) {
        add(h[x], u);
        return;
    }
    int mid = (L + R) / 2;
    update(u * 2, L, mid, l, r, x);
    update(u * 2 + 1, mid + 1, R, l, r, x);
}
int ansL[N], ansR[N], dfn[N], low[N], d[N], cnt, gl[N], gr[N];
int S[N], ins[N], bel[N], siz[N], top, tot;
void tarjan(int x) {
    dfn[x] = low[x] = ++cnt;
    S[++top] = x;
    ins[x] = 1;
    for(auto y : p[x]) {
        if(!dfn[y]) {
            tarjan(y);
            low[x] = min(low[x], low[y]);
        }
        else if(ins[y]) low[x] = min(low[x], dfn[y]);
    }
    if(low[x] == dfn[x]) {
        tot++;
        gl[tot] = 1e18;
        while(1) {
            int now = S[top];
            gl[tot] = min(gl[tot], ll[now]);
            gr[tot] = max(gr[tot], rr[now]);
            ins[now] = 0;
        top--;
        bel[now] = tot;
        if(now == x) break;
        }
    }
}
void SortonGraph() {
queue<int>Q;
for(int i = 1; i <= tot; i++) {
if(d[i] == 0) Q.push(i);
ansL[i] = gl[i];
ansR[i] = gr[i];
    }
        
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(auto y : G[x]) {
ansL[y] = min(ansL[y], ansL[x]);
ansR[y] = max(ansR[y], ansR[x]);
d[y]--;
if(d[y] == 0) Q.push(y);
    }
    }
}
bool P2;
signed main() {
//cerr << (double)(&P1 - &P2) / 1024 / 1024 << "MB" << endl;
    n = read();
    for(int i = 1; i <= n; i++) x[i] = read(), r[i] = read();
    build(1, 1, n);
    for(int i = 1; i <= n; i++) {
    int GetL = -1, GetR = -1;
int L = 1, R = i, mid;
while(L <= R) {
mid = (L + R) / 2;
if(x[i] - r[i] <= x[mid]) {
GetL = mid;
R = mid - 1;
    }
else L = mid + 1;
    } 
L = i, R = n;
while(L <= R) {
mid = (L + R) / 2;
if(x[mid] <= x[i] + r[i]) {
GetR = mid;
L = mid + 1; 
    }
else R = mid - 1;
    }
//cout << i << " : " << GetL << " " << GetR << endl;
update(1, 1, n, GetL, GetR, i);
    }
for(int i = 1; i <= P; i++) 
if(!dfn[i]) tarjan(i);
//for(int i = 1; i <= n; i++) cout << bel[h[i]] << " ";
//cout << endl;
for(int i = 1; i <= P; i++) {
for(auto y : p[i]) {
if(bel[i] != bel[y] && !vis[bel[i]][bel[y]]) {
vis[bel[i]][bel[y]] = 1;
G[bel[y]].push_back(bel[i]);
d[bel[i]]++;
//cout << bel[i] << "->" << bel[y] << endl;
    }
    }
    }

SortonGraph();
int res = 0;
for(int i = 1; i <= n; i++) {
res += i * (ansR[bel[h[i]]] - ansL[bel[h[i]]] + 1), res %= mod;
//cout << i << " : " << ansL[bel[h[i]]] << " " << ansR[bel[h[i]]] << endl;
    }

write(res); 
return 0;
}
​
​
/*
5
0 9
0 9
7 4
8 0
8 0
​
42
*/

P3588 [POI2015] PUS

题意：

给定一个长度为 n 的序列 a 的部分位置的值。需要构造该序列使得满足以下 m 个条件。每个条件给出了 l,r,k 和 k 个数，表示在 [l,r] 的这 k 个数都比其他数大。

\sum k \le 3 \times 10^5。

分析：

先考虑 \sum k 较小时怎么做。

一个很显然的思路是把这 k 个数与另外 r-l+1-k 个数两两连一条边，连 x \rightarrow y 表示 a_y 严格大于 a_x。

如果有环就无解。不会真有人用 tarjan 判环吧，我不说是谁。

那么图就变成了一个 DAG。即可利用拓扑排序。

如果 a_y 被给出的话，就要判断 a_y 是否大于等于 a_x+1，否则就无解。

a_y 没有给出，显然有转移 a_y=\max(a_x+1)。

根据贪心的原则，我们对入度为 0 且没有给出的点，有 a_x=1。

 

但这样做边的数量级是 n^2 的。

对每个条件都新建一个点，记作 x。

一共有 k 个数，划分成了 k+1 段。对这 k 个数，我们称为 k_i，对着 k+1 段我们称为 l_i,r_i。

显然有 [l_i,r_i] \rightarrow x（边权为 0），以及 x \rightarrow k_i（边权为 1）。

边权为 0 表示 a_u \le a_v，边权为 1 表示 a_u < a_v。

显然可以用线段树优化建图。不会去做 模板题。

建图代码如下：

for(int i = 1, l, r, k; i <= m; i++) {
        l = read(), r = read(), k = read();
        cnt++; //对每个限制建立一个源点 
        int L = l, x;
        for(int j = 1; j <= k; j++) { //k把小的数分成了k+1段 
            X[j] = read();
            if(L <= X[j] - 1) update(1, 1, n + m, L, X[j] - 1, cnt, 0); //建边：小的数 <= 源点 
            L = X[j] + 1;
        }
        if(L <= r) update(1, 1, n + m, L, r, cnt, 0);
        for(int j = 1; j <= k; j++) add(h[cnt], h[X[j]], 1); //建边：源点 < 大的数 
}

其他部分跟最开始的暴力方法差不多，不过转移要改成 a_y=\max(a_x+w)。

代码：
#include<bits/stdc++.h>
#define int long long
#define N 1000006
using namespace std;
int read() {
    char ch = getchar(); int x = 0, f = 1;
    while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
    while(ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}
void write(int x) {
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) write(x / 10);
    putchar('0' + x % 10);
}
int n, s, m, cnt, P;
int ans[N], X[N], d[N], o[N], h[N];
struct edge{
    int to, w; //w=0表示x<=to w=1表示x<to 
};
vector<edge>p[N];
void add(int u, int v, int w) {if(u == v && w == 0) return; p[u].push_back((edge){v, w}); d[v]++; }
void build(int u, int L, int R) {
    if(L == R) {
        h[L] = u;
        o[u] = L;
        P = max(P, u);
        return;
    }
    add(u * 2, u, 0);
    add(u * 2 + 1, u, 0);
    int mid = (L + R) / 2;
    build(u * 2, L, mid);
    build(u * 2 + 1, mid + 1, R);
}
void update(int u, int L, int R, int l, int r, int x, int w) {
    if(r < L || R < l) return;
    if(l <= L && R <= r) {
        add(u, h[x], w);
        return;
    }
    int mid = (L + R) / 2;
    update(u * 2, L, mid, l, r, x, w);
    update(u * 2 + 1, mid + 1, R, l, r, x, w);
}
int dfn[N], low[N], tot, ins[N], S[N], top;
void tarjan(int x) { //判断环 
    dfn[x] = low[x] = ++tot;
    S[++top] = x;
    ins[x] = 1;
    for(auto y : p[x]) {
        if(!dfn[y.to]) {
            tarjan(y.to);
            low[x] = min(low[x], low[y.to]);
        }
        else if(ins[y.to]) low[x] = min(low[x], dfn[y.to]);
    }
    if(low[x] == dfn[x]) {
        int num = 0;
        while(1) {
            int now = S[top];
            top--;
            num++;
            ins[now] = 0;
            if(now == x) break;
        }
        if(num > 1) {
        printf("NIE");
        exit(0);
    }
    }
}
int z[N];
bool G[N];
void Sort_On_Graph() {
queue<int>Q;
for(int i = 1; i <= P; i++) 
        if(d[i] == 0) {
        Q.push(i);
        if(!G[o[i]]) z[i] = 1;
    }
while(!Q.empty()) {
int x = Q.front();
        Q.pop();
for(int i = 0; i < p[x].size(); i++) {
int y = p[x][i].to;
if(G[o[y]]) {
if(z[x] + p[x][i].w > z[y]) { //不满足默认值,说明无解 
printf("NIE");  
                exit(0);
    }
    }
else {
if(z[y] != 0) z[y] = max(z[y], z[x] + p[x][i].w);
        else z[y] = z[x] + p[x][i].w;
    }

d[y]--;
if(d[y] == 0) Q.push(y);
    } 
    }
} 
signed main() {
n = read(), s = read(), m = read();
build(1, 1, n + m);
for(int i = 1, p, d; i <= s; i++) {
p = read(), d = read();
ans[p] = d;
z[h[p]] = d; 
G[p] = 1;
    }
cnt = n;
for(int i = 1, l, r, k; i <= m; i++) {
l = read(), r = read(), k = read();
cnt++; //对每个限制建立一个源点 
int L = l, x;
for(int j = 1; j <= k; j++) { //k把小的数分成了k+1段 
X[j] = read();
if(L <= X[j] - 1) update(1, 1, n + m, L, X[j] - 1, cnt, 0); //建边：小的数 <= 源点 
L = X[j] + 1;
    }
if(L <= r) update(1, 1, n + m, L, r, cnt, 0);
for(int j = 1; j <= k; j++) add(h[cnt], h[X[j]], 1); //建边：源点 < 大的数 
    }
for(int i = 1; i <= P; i++) {
if(!dfn[i]) tarjan(i);
    }
Sort_On_Graph();
for(int i = 1; i <= n; i++) {
if(z[h[i]] > 1e9) {
printf("NIE");  
        exit(0);
    }
    }
printf("TAK\n");
for(int i = 1; i <= n; i++) {
write(z[h[i]]);
printf(" ");
    }
return 0;
}