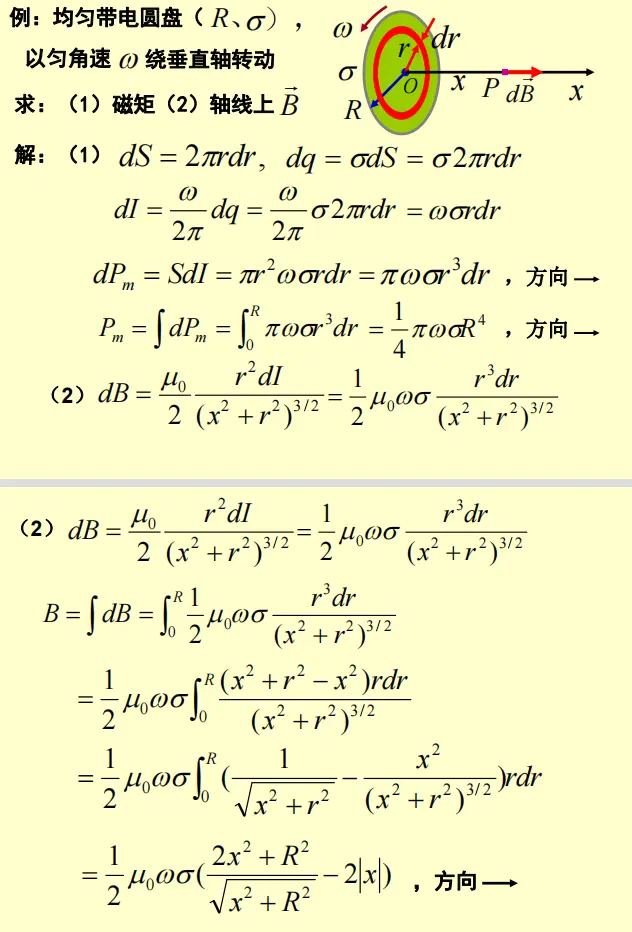第一章 静电场
第一讲 库仑定律
库仑定理——（真空静止点电荷）
\[F = \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2}\boldsymbol{r}^0\tag 1
\]
其中真空介电常数 \(\varepsilon_0 \approx 8.85\times10^{-12} C^2N^{-1}m^{-2}\)，令 \(k=\frac{1}{4\pi\varepsilon_0}\) 则 \(k\approx 9\times 10^9Nm^2/C^2\)，矢量 \(\boldsymbol{r}^0\) 由施力电荷指向受力电荷
第二讲 电场强度\(E\)
2.1 电场强度
\[E = \frac{F}{q_0}=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}\boldsymbol{r}^0\tag 2
\]
2.2 均匀带电细圆环
圆环轴线上一点 \(P\) 的电场强度：
\[E = \frac{1}{4\pi\varepsilon_0}\frac{qx}{(R^2+x^2)^\frac{3}{2}}\tag 3
\]
其中，\(x\) 表示 \(P\) 点到圆环中心 \(O\) 的距离，\(R\) 表示圆环半径，\(q\) 表示圆环带电量；
2.3 有限长直线段
直线外一点 \(P\) 电场强度：
\[E_x=\frac{\lambda}{4\pi\varepsilon_0 a}(cos\theta_1-cos\theta_2), E_y=\frac{\lambda}{4\pi\varepsilon_0 a}(sin\theta_2-sin\theta_1)\tag 4
\]
注：在建立坐标系的情况下，上式均带有方向，其中沿 \(y\) 轴正向：\(\theta_1\rightarrow \theta_2\)，\(\theta\) 为与 \(y\) 轴正向夹角；
其中，\(a\) 表示 \(P\) 点到直线的垂直距离；
2.4 均匀带电无限长直线
由 \(2.4\) 推得：令\(\theta_1=0,\theta_2=\pi\)
\[E_x = \frac{\lambda}{2\pi\varepsilon_0 a}, E_y = 0\tag 5
\]
2.5 均匀带电无限大平面
\[E=\frac{\sigma}{2\varepsilon_0} \tag 6
\]
2.6 无限大均匀带异号电荷平板间
\[E=\frac{\sigma}{\varepsilon_0}\tag 7
\]
其中，\(\sigma\) 表示每个平板的电荷面密度；
2.7 电偶极子
电偶极矩：\(\boldsymbol{p}=q\boldsymbol{l}\)
中垂线上一点\(P\)场强：
\[E = -\frac{\boldsymbol{p}}{4\pi\varepsilon_0y^3} (y\gg l)\tag 8
\]
共线上一点 \(P\) 场强：
\[E=\frac{2\boldsymbol{p}}{4\pi\varepsilon_0x^3}(x\gg l)\tag 9
\]
其中 \(\boldsymbol{l}\) 方向由负电荷指向正电荷；
2.8 力偶矩
电偶极子在匀强电场中得力偶矩：
第三讲 电通量 \(\bigstar\)高斯定理
3.1 电通量
\[\Phi_e=\oint_S\boldsymbol{E}\cdot d\boldsymbol{S}\tag{11}
\]
3.2 高斯定理
选定高斯面后，电通量：
\[\Phi_e=\oint_S\boldsymbol{E}\cdot d\boldsymbol{S}=\frac{1}{\varepsilon_0}\sum_{(内)}q_i\tag{12}
\]
3.3 轴对称性电场
无限长均匀带电直线外一点 \(P\) 场强：
\[\Phi_e=\boldsymbol{E}\oint_侧d\boldsymbol{S}=2\pi rEl=\frac{1}{\varepsilon_0}\lambda l\Rightarrow E = \frac{\lambda}{2\pi\varepsilon_0r}\tag{13}
\]
其中，\(r\)表示 \(P\) 距离导线垂直距离；
3.4 球面对称性电场
均匀带电球面电场分布：
\[\Phi_e=\boldsymbol{E}\oint_S\boldsymbol{S}=E\cdot 4\pi r^2=\sum_{(内)}q_i=q
\]
\[\Rightarrow E=\frac{1}{4\pi \varepsilon_0}\frac{q}{r^2}\boldsymbol{r}^0(r>R)\tag{14}
\]
\[\Rightarrow E=0(r<R)
\]
3.5 无限大均匀带电平面
选定圆柱面作为高斯面：
\[\Phi_e=\oint_{左端面}\boldsymbol{E}\cdot d\boldsymbol{S}+\oint_{右端面}\boldsymbol{E}\cdot d\boldsymbol{S}=2ES=\frac{1}{\varepsilon_0}\sigma S\tag{15}
\]
3.6 均匀带电圆盘
\[E = \frac{\sigma}{2\varepsilon_0}(1-\frac{x}{\sqrt{R^2+x^2}})\tag{16}
\]
3.7 均匀带电球体
\[E=\frac{Q}{4\pi\varepsilon_0r^2}\boldsymbol{r_0}(r>R)
\]
\[E=\frac{\rho}{3\varepsilon_0}\boldsymbol{r}(r<R)
\]
第四讲 静电场的环路定理 电势能
4.1 电场强度环流
\[\oint\boldsymbol{E}\cdot d\boldsymbol{l}=0\tag{17}
\]
环路定理表明静电场是无旋有源场；
4.2 电势能
选定电势能零参考点，则点 \(A\) 处的电势能：
\[w_a=A_{a'0'}=\int_a^{'0'}q_0\boldsymbol{E}\cdot d\boldsymbol{l}\tag{18}
\]
注：电势能是标量，相对于电势能零参考点有负值；
第五讲 电势 电势差
5.1 电势与电势差
\(A\)点电势：
\[u_a=\frac{W_a}{q_0}=\int_a^{'0'}\boldsymbol{E}\cdot d\boldsymbol{l}\tag{19}
\]
注：电势为标量；
\[U_{ab}=u_a-u_b=\int_a^b\boldsymbol{E}\cdot d\boldsymbol{l}\tag{20}
\]
电荷\(q\)\(a\rightarrow b\)时，静电力做功：
\[A_{ab}=q(u_a-u_b)\tag{21}
\]
5.2 电偶极子电势能
在电场 \(\boldsymbol{E}\) 中：
\[W=-\boldsymbol{p}\cdot\boldsymbol{E}\tag{22}
\]
当\(\boldsymbol{E}\)为非均匀电场时，上式应改为积分形式；在电场中做功：
- 方法一
\[W_{\theta_1\theta_2}=-\boldsymbol{p}\cdot\boldsymbol{E}(\theta_1)-(-\boldsymbol{p}\cdot\boldsymbol{E}(\theta_2))
\]
- 方法二
\[W_{\theta_1\theta_2}=\int_{\theta_1}^{\theta_2}-\boldsymbol{p}\times\boldsymbol{E}d\theta
\]
5.3 电势叠加原理
对于点电荷选取无穷远处作为零电势点：
\[u_a=\int_a^{\infty}\boldsymbol{E}\cdot d\boldsymbol{l}=\frac{1}{4\pi\varepsilon_0}\frac{q}{r}\\
W_a = \frac{1}{4\pi\varepsilon_0}\frac{q^2}{r}\tag{23}
\]
叠加原理——标量叠加
\[u_a=\sum u_i\\
\Rightarrow u_a=\int_Q\frac{1}{4\pi\varepsilon_0}\frac{dq}{r}\tag{24}
\]
5.4 电荷分布求电势
积分形式：
\[u_a=\int_Q\frac{1}{4\pi\varepsilon_0}\frac{dq}{r}\tag{25}
\]
电偶极子外任一点\(C\)的电势：
\[U_C = \frac{1}{4\pi\varepsilon_0}\frac{q}{r_+}-\frac{1}{4\pi\varepsilon_0}\frac{q}{r_-}=\frac{q}{4\pi\varepsilon_0}\frac{r_--r_+}{r_-r_+}
\]
\[r\gg l\Rightarrow r_+r_-\approx r^2,r_--r_+\approx lcos\theta\tag{26}
\]
\[\Rightarrow u_C = \frac{1}{4\pi\varepsilon_0}\frac{\boldsymbol{p}\cdot\boldsymbol{r}}{r^3}
\]
5.5 电场强度求电势
场强与电势关系：
\[u_a=\int_a^{\infty}\boldsymbol{E}\cdot d\boldsymbol{l}\tag{27}
\]
带电体电荷分布具有对称性时，利用高斯定理求出场强分布进而求电势；
【无限长均匀带电圆柱面】
由高斯定理求得电场分布：
一般而言，当电荷分布延伸到无穷远时，是不能选取无穷远处为电势零参考点的；
\[u_P=\int_P^{P_0}\boldsymbol{E}\cdot d\boldsymbol{l}=\int_P^{P'}\boldsymbol{E}\cdot d\boldsymbol{l}+\int_{P'}^{P_0}\boldsymbol{E}\cdot d\boldsymbol{l}
\]
\[=0+\int_r^{r_0}\frac{\lambda}{2\pi\varepsilon_0r}dr
=-\frac{\lambda}{2\pi\varepsilon_0}\ln r+\frac{\lambda}{2\pi\varepsilon_0}\ln r_0\tag{29}
\]
\[=-\frac{\lambda}{2\pi\varepsilon_0}\ln r+C(r>R)
\]
\[u_P=\int_P^{P_0}\boldsymbol{E}\cdot d\boldsymbol{l}=\int_r^R\boldsymbol{E}\cdot d\boldsymbol{l}+\int_R^{r_0}\boldsymbol{E}\cdot d\boldsymbol{l}
\]
\[=0+\int_R^{r_0}\frac{\lambda}{2\pi\varepsilon_0r}dr\tag{30}
\]
\[=-\frac{\lambda}{2\pi\varepsilon_0}\ln R + C(r<R)
\]
其中，\(C=\frac{\lambda}{2\pi\varepsilon_0}\ln r_0\)
5.6 均匀带电球面电势
5.7 均匀带电球体电势
球内距离球心\(r\)处一点\(P\)电势：
\[u = u_1+u_2=\frac{1}{4\pi\varepsilon_0}\frac{Q}{R^3}r^2+\int_r^R\frac{1}{4\pi\varepsilon_0}\frac{dq_2}{r'}
\]
\[=\frac{1}{4\pi\varepsilon_0}\frac{Q}{R^3}r^2+\int_r^R\frac{3Qr'}{4\pi\varepsilon_0R^3}dr'\tag{32}
\]
\[=\frac{Q(3R^2-r^2)}{8\pi\varepsilon_0R^3}(r<R)
\]
球外距离球心 \(r\) 处一点 \(P\) 电势：
\[u = \frac{Q}{4\pi\varepsilon_0r}(r\ge R)\tag{33}
\]
注：在 \(P\) 点的电场强度犹如电荷集中在球心处的点电荷在 \(P\) 点产生的电场强度一样，故电势同理；
第六讲 电势与场强微分关系
\[E = -\frac{du}{dn}, E_l=-\frac{du}{dl}
\]
\[\boldsymbol{E}=-(\frac{\partial u}{\partial x}\boldsymbol{i}+\frac{\partial u}{\partial y}\boldsymbol{j}+\frac{\partial u}{\partial z}\boldsymbol{k}), u(x,y,z)\Rightarrow E(x,y,z)\tag{34}
\]
第七讲 静电场中的导体 电容
7.1 静电平衡导体表面
电场强度：
\[\boldsymbol{E}=\frac{\sigma}{\varepsilon_0}\boldsymbol{n}\tag{35}
\]
区别于无限大带电平面产生的电场(缺少静电平衡的条件)：
\[\boldsymbol{E}=\frac{\sigma}{2\varepsilon_0}\boldsymbol{n}\tag{36}
\]
7.2 孤立导体电容
\[C = \frac{q}{u}\tag{37}
\]
7.3 平行板电容器电容
\[C = \frac{q}{u_1-u_2}\\
=\frac{q}{Ed}=\frac{q}{\frac{\sigma}{\varepsilon_0}d}\\
=\frac{q}{\frac{qd}{\varepsilon_0S}}=\frac{\varepsilon_0S}{d}\tag{38}
\]
7.4 球形电容器电容
两球面间电场强度：
\[E=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}\tag{39}
\]
\[u_1-u_2=\int_{R_1}^{R_2}\boldsymbol{E}\cdot d\boldsymbol{l} = \int_{R_1}^{R_2}\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}dr
\]
\[=\frac{q}{4\pi\varepsilon_0}\frac{R_2-R_1}{R_1R_2}\tag{40}
\]
\[\Rightarrow C = \frac{q}{u_1-u_2}=\frac{4\pi\varepsilon_0R_1R_2}{R_2-R_1}
\]
7.5 电容器串并联
- 串联
\[\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\cdot\cdot\cdot+\frac{1}{C_n}
\]
- 并联
\[C = C_1+C_2+\cdot\cdot\cdot+C_n\tag{41}
\]
第八讲 静电能
8.1 静电能公式推导
\[U(t) = \frac{q(t)}{C}, dA = U(t)dq = \frac{q(t)}{C}dq
\]
\[A = \int dA = \int_0^Q\frac{q(t)}{C}dq=\frac{Q^2}{2C}
Q=CU\tag{42}
\]
\[\Longrightarrow A = \frac{1}{2}CU^2=\frac{1}{2}QU\Rightarrow W=A=\frac{Q^2}{2C}=\frac{1}{2}CU^2=\frac{1}{2}QU
\]
8.2 电场能量密度推导
\[U=Ed, C = \frac{\varepsilon_0S}{d}
\]
\[\Rightarrow W = \frac{1}{2}\varepsilon_0E^2Sd = \frac{1}{2}\varepsilon_0E^2V\tag{43}
\]
\[\Rightarrow \omega = \frac{W}{V}=\frac{1}{2}\varepsilon_0E^2
\]
第九讲 电介质的极化 束缚电荷
9.1 电介质
\[C = \varepsilon_r C_0\tag{44}
\]
其中，\(\varepsilon_r\) 称为介质的相对介电常数（相对电容率），\(C_0\) 表示真空中对应的电容；因此，除真空中 \(\varepsilon_r=1\) 外，其余 \(\varepsilon_r>1\)；
9.2 介质极化
{% message color:info size:default%}
有极分子 \(\Rightarrow\) 取向极化
无极分子 \(\Rightarrow\) 位移极化
第十讲 电介质内的电场强度
根据电介质极化原理推导：
\[\boldsymbol{E} = \boldsymbol{E}_0+\boldsymbol{E}',\ E_0=\frac{\sigma_0}{\varepsilon_0},E'=\frac{\sigma'}{\varepsilon_0}
\]
\[\Rightarrow E = \frac{\sigma_0}{\varepsilon_0}-\frac{\sigma'}{\varepsilon_0},\ E = \frac{E_0}{\varepsilon_r}\tag{45}
\]
\[\Rightarrow \sigma'=(1-\frac{1}{\varepsilon_r})\sigma_0
\]
第十一讲 \(\bigstar\)电介质中的高斯定理
11.1 电位移矢量
推导：
\[\iint_S\boldsymbol{E}\cdot d\boldsymbol{S}=\frac{1}{\varepsilon_0}(\sigma_0-\sigma')S
\]
由式(45)得:
\[\frac{1}{\varepsilon_0}(\sigma_0-\sigma')=\frac{\sigma_0}{\varepsilon_0\varepsilon_r}
\]
\[\iint_S\varepsilon_0\varepsilon_r\boldsymbol{E}\cdot d\boldsymbol{S}=\varepsilon_0S=q_0
\]
令 \(\boldsymbol{D} = \varepsilon\boldsymbol{E} = \varepsilon_0\varepsilon_r\boldsymbol{E}\) 得:
\[\iint_S\boldsymbol{D}\cdot d\boldsymbol{S} = q_0\tag{46}
\]
其中，\(D\) 称为电位移矢量或电通密度，\(\varepsilon = \varepsilon_0\varepsilon_r\) 称为电介质的介电常数；
11.2 电介质中的能量密度
\[\omega = \frac{1}{2}\boldsymbol{D}\cdot\boldsymbol{E}\\
\varepsilon_r = 1\Rightarrow \omega = \frac{1}{2}\varepsilon_0E^2\tag{47}
\]
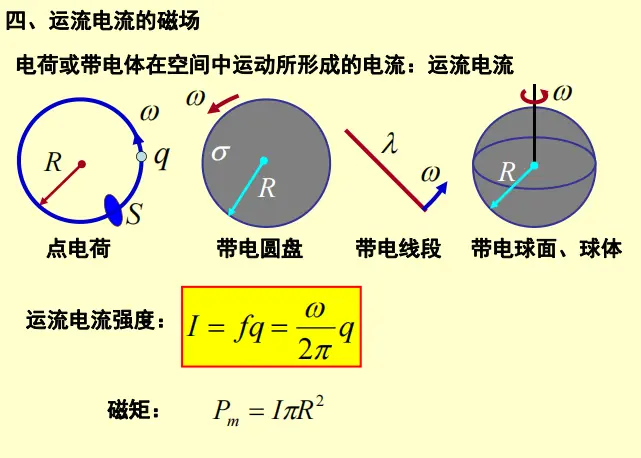
第二章 恒定电流的磁场
第一讲 磁感应强度\(B\)
电流元 \(Idl\) 所受磁场力：
\[d\boldsymbol{F} = Id\boldsymbol{l}\times\boldsymbol{B}\tag{1}
\]
第二讲 毕奥-萨伐尔定律
2.1 电流元的磁场
\[d\boldsymbol{B} = \frac{\mu_0}{4\pi}\frac{Id\boldsymbol{l}\times\boldsymbol{r}^0}{r^2}\tag{2}
\]
其中，\(\mu_0=4\pi\times10^{-7}N/A^2\)称为真空磁导率，\(\boldsymbol{r}_0\) 表示到 \(P\) 点的单位矢量，\(r\) 表示到 \(P\) 点的距离；
2.2 运动电荷的磁场
\[\boldsymbol{B} = \frac{d\boldsymbol{B}}{dN}=\frac{\mu_0}{4\pi}\frac{q\boldsymbol{v}\times\boldsymbol{r}^0}{r^2}\tag{3}
\]
2.3 载流直导线的磁场
\[dB = \frac{\mu_0}{4\pi}\frac{Idlsin\theta}{r^2}
\]
\[\Rightarrow B = \frac{\mu_0I}{4\pi r}\int_{\theta_1}^{\theta_2}sin\theta d\theta=\frac{\mu_0I}{4\pi r}(cos\theta_1-cos\theta_2)\tag{4}
\]
\[\theta_1\approx 0,\theta_2\approx\pi\Rightarrow B = \frac{\mu_0I}{2\pi r}
\]
式中，\(r\) 表示到载流导线的距离；
2.4 载流圆环的磁场
\[B = \int dB_x = \int dBcos\theta = \frac{\mu_0}{4\pi}\int \frac{Idl}{r^2}cos\theta
\]
\[cos\theta = \frac{R}{r}=\frac{R}{(R^2+x^2)^{1/2}}\tag{5}
\]
\[\Rightarrow B = \frac{\mu_0IR^2}{2(R^2+x^2)^{3/2}}
\]
【\(N\)匝线圈】
\[B = \frac{\mu_0IR^2N}{2(R^2+x^2)^{3/2}}\tag{6}
\]
【圆弧磁场】
由式 (5) 令 \(x=0\) 得圆心处磁感应强度: \(B = \frac{\mu_0I}{2R}\)
\[B = \frac{\mu_0I}{2R}\cdot\frac{\varphi}{2\pi}=\frac{\mu_0I\varphi}{4\pi R}\tag{7}
\]
2.5 载流线圈的磁矩
由式 (5) 令 \(x\gg R\) 则得: \((x^2+R^2)\approx x^2\)
\[\Rightarrow B\approx \frac{\mu_0IR^2}{2x^3} = \frac{\mu_0I\pi R^2}{2\pi x^3}=\frac{\mu_0 IS}{2\pi x^3}
\]
\[\Rightarrow Define:\ \ \ \ \boldsymbol{p}_m = IS\boldsymbol{n}\tag{8}
\]
\[\boldsymbol{B} = \frac{\mu_0}{2\pi}\frac{\boldsymbol{p}_m}{x^3}
\]
其中，\(\boldsymbol{n}\)表示线圈平面正法线方向上的单位矢量；
圆心处的磁感应强度：
\[\boldsymbol{B} = \frac{\mu_0}{2\pi}\frac{\boldsymbol{p}_m}{R^3}\tag{9}
\]
2.6 无限大均匀载流平面
\[dB = \frac{\mu_0\alpha dx}{2\pi\sqrt{r^2+x^2}}
\]
由对称性得：\(B_x = \int dB_x, \ \ \ B_y = \int dB_y = 0\)
\[B = B_x = \int \frac{r}{\sqrt{r^2+x^2}}\cdot \frac{\mu_0 \alpha dx}{2\pi\sqrt{r^2+x^2}} =\int \frac{\mu_0 \alpha r dx}{2\pi (r^2+x^2)}
\]
\[=\frac{\mu_0 \alpha r}{2\pi}\int_{-\infty}^{+\infty}\frac{1}{r^2+x^2}dx=\frac{\mu_0 \alpha}{2}\tag{10}
\]
\[\Longrightarrow B = \frac{1}{2}\mu_0\alpha
\]
式中，\(r\) 表示\(P\)点距到无限大载流平面的距离，\(\alpha\) 表示流过单位长度的电流；
2.7 均匀密绕直螺线管
\[dB = \frac{\mu_0R^2dI'}{2(R^2+l^2)^{3/2}} = \frac{\mu_0R^2Indl}{2(R^2+l^2)^{3/2}}
\]
\[l = Rcot\beta\ ,\ \ \ dl = -Rcsc^2\beta d\beta\ , \ \ \ R^2+l^2 = R^2csc^2\beta
\]
\[\Rightarrow dB= -\frac{\mu_0}{2}nIsin\beta d\beta\tag{11}
\]
\[\Rightarrow B =\int_{\beta_1}^{\beta_2}-\frac{\mu_0}{2}nIsin\beta d\beta = \frac{\mu_0nI}{2}(cos\beta_2-cos\beta_1)
\]
【无限长】
\[L\gg R,\ \ \beta_1\rightarrow\pi, \ \ \beta_2\rightarrow 0 \Rightarrow B = \mu_0nI\tag{12}
\]
【半无限长】
端点处：
\[\beta_1 = \frac{\pi}{2}, \ \ \beta_2\rightarrow 0\ , or \ \ \beta_1\rightarrow \pi, \ \ \beta_2=\frac{\pi}{2}\Rightarrow B = \frac{\mu_0nI}{2}\tag{13}
\]
式中，\(n\) 表示单位长度上的线圈匝数；
2.8 均匀密绕圆环螺线管
\[B = n\mu I
\]
第三讲 磁通量 磁场的高斯定理
3.1 磁通量
\[\Phi_m = \int_S \boldsymbol{B}\cdot d\boldsymbol{S}\tag{14}
\]
3.2 高斯定理
\[\oint_S \boldsymbol{B}\cdot d\boldsymbol{S}=0\tag{15}
\]
第四讲 \(\bigstar\)安培环路定理
\[\oint_L\boldsymbol{B}\cdot d\boldsymbol{l}=\mu_0\sum_{(内)}I_i\tag{16}
\]
式中，\(I_i\) 的正（负）取决于电流方向与闭合路径 \(L\) 绕行方向满足（不满足）右螺旋法则；\(B\) 表示闭合路径 \(L\) 内外所有电流产生的总磁感应强度；
【无限大载流平面】
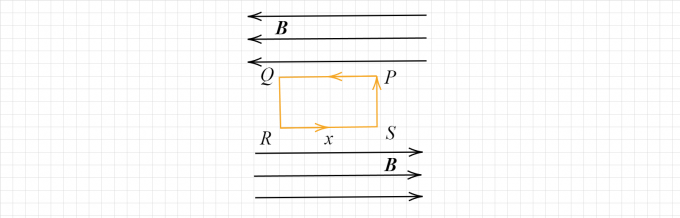
\[\oint_L\boldsymbol{B}\cdot d\boldsymbol{l} = \int_{PQ}\boldsymbol{B}\cdot d\boldsymbol{l}+\int_{QR}\boldsymbol{B}\cdot d\boldsymbol{l}+\int_{RS}\boldsymbol{B}\cdot d\boldsymbol{l}+\int_{SP}\boldsymbol{B}\cdot d\boldsymbol{l}
\]
\[=Bx+0+Bx+0 = 2Bx = \mu_0 \alpha x\tag{17}
\]
\[\Rightarrow B = \frac{1}{2}\mu_0\alpha
\]
第五讲 磁场对电流作用
5.1 载流导线
所受安培力：
\[\boldsymbol{F} = \int_LId\boldsymbol{l}\times\boldsymbol{B}\tag{18}
\]
5.2 载流线圈
所受磁力矩：
\[M = F_{ab}l_1sin\varphi=BIl_1l_2sin\varphi=BISsin\varphi
\]
\[\boldsymbol{p}_m = IS\boldsymbol{n}\tag{19}
\]
\[\Rightarrow \boldsymbol{M}=\boldsymbol{p}_m\times\boldsymbol{B}
\]
式中，\(\boldsymbol{n}\) 的方向按电流方向用右螺旋法则确定；
5.3 磁力的功
\[A = F\overline{aa'} = BIl\overline{aa'}=BI\vartriangle S = I\vartriangle\Phi
\]
\[\Rightarrow A = \int_{\Phi_1}^{\Phi_2}Id\Phi = I(\Phi_2-\Phi_1)=I\vartriangle\Phi\tag{20}
\]
5.4 磁偶极子势能
载流线圈相当于磁偶极子，因此载流线圈同理；
当 \(\varphi = \frac{\pi}{2}\) 时, \(W = 0\) (零势能点)
\[W = -A = -\int_\varphi^{\pi/2}Md\varphi = -p_mB\int_\varphi^{\pi/2}sin\varphi d\varphi = -p_mBcos\varphi
\]
\[\Rightarrow W = -\boldsymbol{p}_m\cdot \boldsymbol{B}\tag{21}
\]
第六讲 带电粒子在电场和磁场中的运动
6.1 洛伦兹力
\[\boldsymbol{F} = q\boldsymbol{v}\times\boldsymbol{B}\tag{22}
\]
式中，\(q\) 包含电荷正负特性符号；
6.2 霍尔效应
\[q\overline{v}B=qE\Rightarrow E = \overline{v}B\Rightarrow U = El = vBl
\]
\[I = nqS\overline{v}\Rightarrow U = \frac{IB}{nqd} = K\frac{IB}{d}\tag{23}
\]
\[K = \frac{1}{nq}
\]
式中，\(d\) 和 \(l\) 分别表示沿电流方向上导体截面的宽度和高度；\(n\) 表示单位体积的载流子数；
【载流子种类】
- p(positive)型半导体 \(\Rightarrow\) 空穴 \(\Rightarrow\) 空穴导电
- n(negative)型半导体 \(\Rightarrow\) 电子 \(\Rightarrow\) 电子导电
- 金属导体(大多数) \(\Rightarrow\) 电子 \(\Rightarrow\) 电子导电
第七讲 磁介质
7.1 相对磁导率
\[\mu_r = \frac{B}{B_0}\tag{24}
\]
式中，\(B_0\) 表示真空磁感应强度，\(\mu_r\) 表示磁介质的相对磁导率，\(B\) 表示磁介质的磁感应强度；
- \(\mu_r > 1\Rightarrow\) 顺磁质(弱/非磁性物质)
- \(\mu_r<1\Rightarrow\) 抗磁质(弱/非磁性物质)
- \(\mu_r\gg 1 \Rightarrow\) 铁磁质(强磁性物质)
7.2 \(\bigstar\) 磁介质的安培环路定理
\[\oint_L\boldsymbol{B}\cdot d\boldsymbol{l} = \mu_0\mu_r\sum_{(内)}I
\]
令 \(\mu = \mu_0\mu_r\) 得:
\[\oint_L \frac{\boldsymbol{B}}{\mu}\cdot d\boldsymbol{l}=\sum_{(内)}I
\]
令 \(\boldsymbol{H} = \frac{\boldsymbol{B}}{\mu}\) 得:
\[\oint_L\boldsymbol{H}\cdot d\boldsymbol{l}=\sum_{(内)}I\tag{25}
\]
式中，\(\mu\) 表示磁介质的磁导率，\(\boldsymbol{H}\) 表示磁场强度，对有介质存在的环路定理的处理可以参考电位移矢量 \(\boldsymbol{D}\)；
第八讲 经典习题
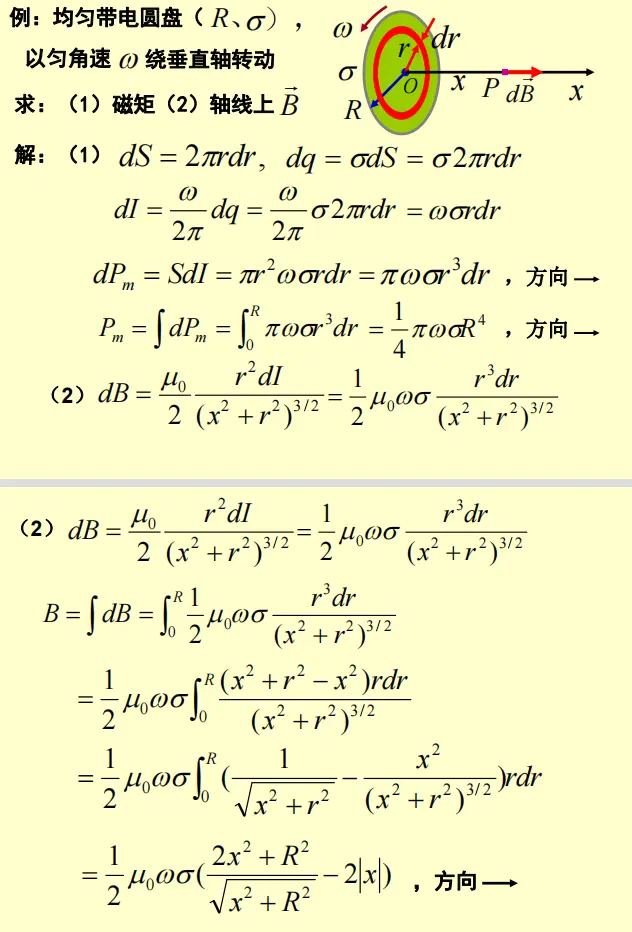
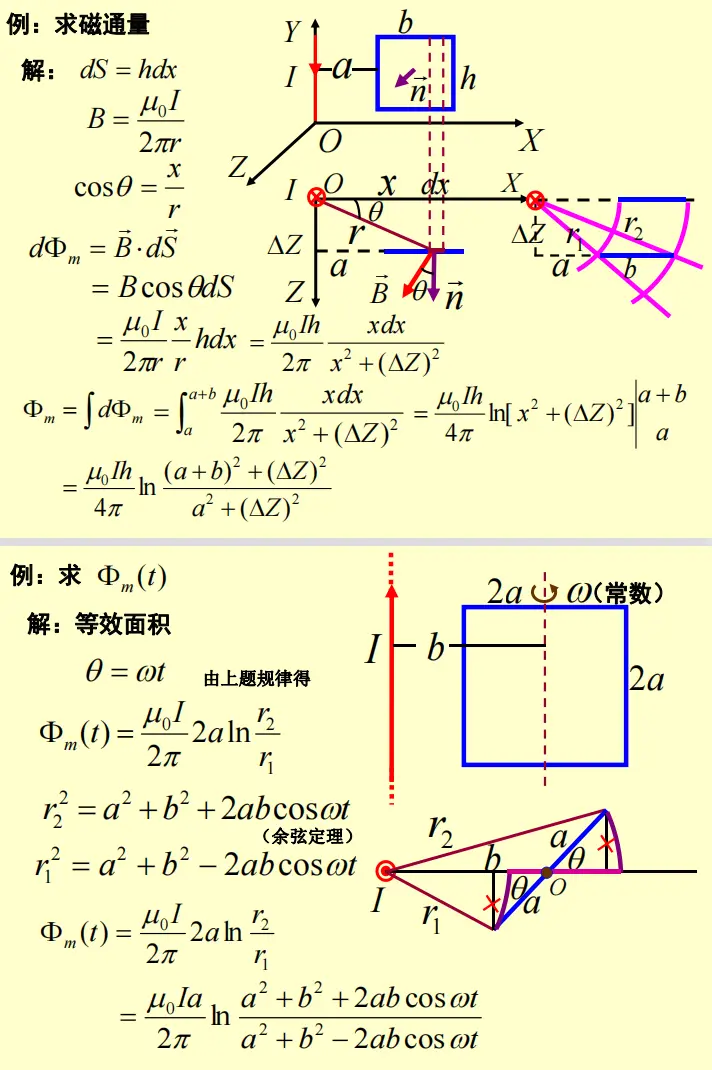
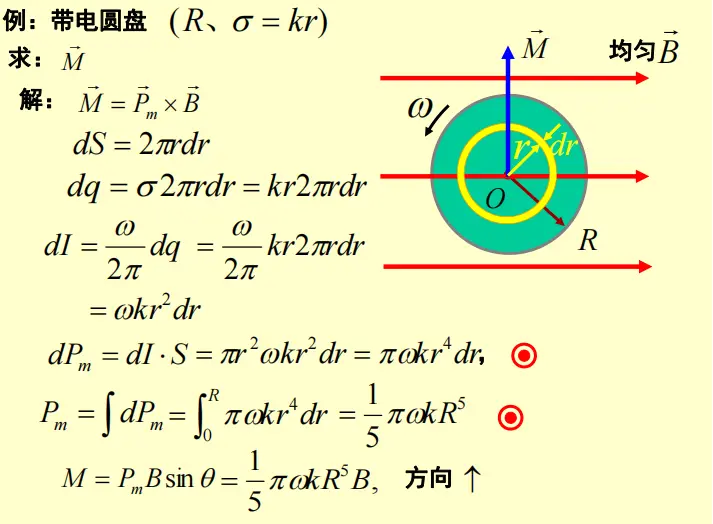
第三章 电磁感应与电磁场
第一讲 电磁感应的基本规律
1.1 电动势
闭合回路上：
\[\xi = \oint\boldsymbol{E}_k\cdot d\boldsymbol{l}\tag{1}
\]
对于一段电路\(ab\)：
\[\xi = \int_a^b\boldsymbol{E}_k\cdot d\boldsymbol{l}\tag{2}
\]
其中，\(\boldsymbol{E}_k\)表示非静电性电场强度；
1.2 法拉第电磁感应定律
\[\xi_i=-\frac{d\Phi}{dt}\tag{3}
\]
由楞次定律确定方向\(\Rightarrow\)方向相反；
1.3 多匝串联线圈
\[\xi_i=-\frac{d}{dt}(\sum_{k=1}^N\Phi_k)=-\frac{d\Psi}{dt}\tag{4}
\]
\[\xi_i=-\frac{d\Psi}{dt}=-N\frac{d\Phi}{dt}(\Phi_i=\Phi_j, 1 \leq i,j \leq N)\tag{5}
\]
其中，\(\Psi=\sum_{k=1}^N\Phi_k\)表示穿过各线圈的总磁通量，称为磁通链数；
1.4 长直螺线管
在长直螺线管外套一 \(N\) 匝，总内阻为 \(R\) 的圆线圈，\(S\) 表示螺线管截面积：
\[B=\mu_0nI\Rightarrow \Phi = \boldsymbol{B}\cdot\boldsymbol{S}=\mu_0nIS
\]
当通电电流均匀变化时，螺线管内的感应电动势:
\[\xi_i=-\frac{d\Psi}{dt}=-N\frac{d\Phi}{dt}=-\mu_0nNS\frac{dI}{dt}
\]
【螺线管内磁感应强度】
感应电流 \(I_i=\frac{\xi_i}{R}=-\frac{N}{R}\frac{d\Phi}{dt}\)
\[\Delta_{q_i}=\int_{t_1}^{t_2}I_idt=-\frac{N}{R}\int_{\Phi_1}^{\Phi_2}d\Phi=-\frac{N}{R}(\Phi_2-\Phi_1)
\]
\[\Longrightarrow \Phi_1-\Phi_2=\frac{\Delta_{q_i}R}{N}
\]
当 \(\Phi_1=0\vert_{t=t_1},\Phi_2=BS\vert_{t=t_2\rightarrow+\infty}\) 时，推出 \(B=\frac{\Delta_{q_i}R}{NS}\)
第二讲 动生电动势 感生电动势
2.1 动生电动势
导体棒 \(ab\) 产生的动生电动势：
\[\xi_i=\int_a^b\boldsymbol{E}_k\cdot d\boldsymbol{l}=\int_a^b(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{l}\tag{6}
\]
闭合回路产生的动生电动势：
\[\xi_i=\oint_Ld\xi_i=\oint_L(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{l}\tag{7}
\]
动生电动势方向由 \(\boldsymbol{v}\times\boldsymbol{B}\cdot d\boldsymbol{l}\) 判定：
注：积分路径：\(a\rightarrow b\)，在电源内部非静电性电场强度从负极指向正极， \(\boldsymbol{E}_k\) 与积分方向一致时积分值为正，否则为负；
2.2 感生电动势
| 感生电场假说\(\Longrightarrow\) 有旋电场 |
|---|
【回路固定不动】
\[\xi_i=\oint_L\boldsymbol{E}_V\cdot d\boldsymbol{l}=-\iint_S\frac{\partial \boldsymbol{B}}{\partial t}\cdot d\boldsymbol{S}\tag{9}
\]
感生电动势方向由楞次定律判定；有旋电场度 \(E_V\) 的方向判定：闭合回路由右螺旋法则指向磁场方向选定回路绕行正方向，由式 \((9)\) 代入符号计算，\(E_V\) 正负与回路绕行方向保持一致；
当 \(E_V\) 相等，磁场均匀变化时，
\[\xi_i=E_V\oint_Ldl=-\frac{\partial{B}}{\partial{t}}\iint_SdS=-\frac{\partial{B}}{\partial{t}}S\tag{10}
\]
第三讲 自感与互感
3.1 自感电动势
\[\Psi=LI\Rightarrow \xi_L=-\frac{d\Psi}{dt}=-L\frac{dI}{dt}\tag{11}
\]
式中 \(L\) 表示自感系数为常量，与 \(I\) 无关(存在铁磁质时与 \(I\) 有关)，仅有回路的匝数、几何形状、大小以及周围介质磁导率决定；
3.2 长直螺线管自感系数
【空心自感线圈】
\[B = \mu_0nI=\mu_0\frac{N}{l}I\Rightarrow \Psi=NBS=\mu_0\frac{N^2}{l}\pi R^2I
\]
\[\Longrightarrow L=\frac{\Psi}{I}=\frac{\mu_0N^2\pi R^2}{l}=\mu_0n^2V\ (V=\pi R^2l)\tag{12}
\]
3.3 传输线的分布电感
两长直平行导线电流 \(I\)，半径 \(r_0\)，轴线间距 \(d\)，且 \(r_0\leq d\)；
导线微元: \(d\Phi_1=BdS=\frac{\mu_0I}{2\pi r}ldr\)
\[\Rightarrow \Phi_1=\int_{r_0}^{d-r_0}\frac{\mu_0Il}{2\pi}\frac{dr}{r}=\frac{\mu_0Il}{2\pi}\ln(\frac{d-r_0}{r_0})
\]
3.4 互感电动势
- 回路 \(1\) 对回路 \(2\): \(\Psi_{21}=M_{21}I_1\)
- 回路 \(2\) 对回路 \(1\): \(\Psi_{12}=M_{12}I_2\)
\[M_{21}=M_{12}=M\Longrightarrow \xi_M=-M\frac{dI}{dt}\tag{14}
\]
式中 \(M_{21}\) 表示回路 \(1\) 对回路 \(2\) 的互感系数，\(M_{12}\) 表示回路 \(2\) 对回路 \(1\) 的互感系数；\(M\) 表示两个回路间的互感系数，与 \(I\) 无关(存在铁磁质时与 \(I\) 有关)，由回路的匝数、几何形状、尺寸、周围介质磁导率以及回路的相对位置决定；
| \(M_{12}=M_{21}=M\Rightarrow\) 转换研究对象简化计算互感系数\(\Rightarrow\) 互感电动势 |
|---|
第四讲 磁能
4.1 自感磁能
\[dA=-\xi_Lidt,\ \xi_L=-L\frac{di}{dt}
\]
\[\Longrightarrow dA=Lidi
\]
\[\Longrightarrow A=\int_0^ILidi=\frac{1}{2}LI^2\tag{15}
\]
| 即\(W_m=\frac{1}{2}LI^2\) (自感磁能) |
|---|
| 当有磁场能量时可以利用\(L=\frac{2W_m}{I^2}\) 计算自感系数 |
式中，\(L\) 表示线圈自感，\(I\) 表示线圈所通电流；
4.2 长直螺线管磁能
\[由式(12)\Rightarrow L=\mu n^2V\Rightarrow W_m=\frac{1}{2}LI^2=\frac{1}{2}\mu n^2I^2V
\]
\[B=\mu nI\Longrightarrow H=\frac{B}{\mu}=nI\tag{16}
\]
| \(W_m=\frac{1}{2}BHV\) |
|---|
| 磁能密度\(\omega_m=\frac{W_m}{V}=\frac{1}{2}BH=\frac{1}{2}\frac{B^2}{\mu_0\mu_r}\) |
4.3 有限体积内的磁能
\[W_m=\int_VdW_m=\frac{1}{2}\int_VBHdV\tag{17}
\]
第五讲 麦克斯韦电磁场理论
5.1 位移电流
- 传导电流 \(\Leftarrow\) 电荷定向移动形成的电流
- 位移电流 \(\Leftarrow\) 电位移通量的变化率(变化的电场)
\[\Phi_D=DS=\varepsilon ES=\varepsilon\cdot\frac{\sigma}{\varepsilon}S=\sigma S
\]
- 传导电流
\[\Longrightarrow \frac{d\Phi}{dt}=\frac{d}{dt}(\sigma S)=\frac{dq}{dt}=I\tag{18}
\]
- 位移电流
\[\Longrightarrow I_D = \frac{d\Phi_D}{dt}=\frac{dD}{dt}S=\varepsilon\frac{dE}{dt}S
\]
- 全电流
| 非恒定电路中传导电流不连续但全电流保持连续 |
|---|
5.2 全电流安培环路定理
\[\oint_L\boldsymbol{H}\cdot d\boldsymbol{l}=I+I_D,\ I_D =\frac{d\Phi_D}{dt}= \int_S\frac{d\boldsymbol{D}}{dt}\cdot\boldsymbol{S}\tag{19}
\]
5.3 麦克斯韦方程组
-
电场 \(\boldsymbol{E}, \boldsymbol{D}\)
- 自由电荷产生的静电场 \(\boldsymbol{E_1}\)、\(\boldsymbol{D_1}\)
-
$\Rightarrow\boldsymbol{E}=\boldsymbol{E_1}+\boldsymbol{E_2}$ - 变化磁场产生的有旋电场 \(\boldsymbol{E_2}\)、\(\boldsymbol{D_2}\)
-
$\Rightarrow\boldsymbol{D}=\boldsymbol{D_1}+\boldsymbol{D_2}$
-
磁场 \(\boldsymbol{B}, \boldsymbol{H}\)
- 传导电流产生的磁场 \(\boldsymbol{B_1}\)、\(\boldsymbol{H_1}\)
-
$\Rightarrow\boldsymbol{B}=\boldsymbol{B_1}+\boldsymbol{B_2}$ - 位移电流产生的磁场 \(\boldsymbol{B_2}\)、\(\boldsymbol{H_2}\)
-
$\Rightarrow\boldsymbol{H}=\boldsymbol{H_1}+\boldsymbol{H_2}$
| 电场的高斯定理 | \(\oint_S\boldsymbol{D}\cdot d\boldsymbol{S}=\sum_iq_i\) | 电场是有源场 |
|---|---|---|
| 法拉第电磁感应定律 | \(\oint_L\boldsymbol{E}\cdot d\boldsymbol{l}=-\iint_S\frac{\partial{\boldsymbol{B}}}{\partial{t}}\cdot d\boldsymbol{S}\) | 静电场是保守(无旋、有势)场 |
| 磁场的高斯定理 | \(\oint_S\boldsymbol{B}\cdot d\boldsymbol{S}=0\) | 磁场是无源场 |
| 全电流安培环路定理 | \(\oint_L\boldsymbol{H}\cdot d\boldsymbol{l}=\sum(I_D+I)\) | 磁场是有旋(非保守)场 |
- 位移电流 \(I_d\)
\[\Phi_D = \iint\boldsymbol{D}\cdot d\boldsymbol{S}\\
I_d = \frac{d\Phi_D}{dt}
\]
第四章 狭义相对论力学基础
第一讲 力学相对性原理
1.1 经典力学相对性原理
| 力学相对性原理 |
|---|
| 对于描述力学现象的规律而言，所有惯性系都是等价的 |
| 力学规律的数学表达式应具有伽利略坐标变换的不变性(协变性) |
1.2 伽利略坐标变化式
根据 \(\lambda_{PS'}+\lambda_{S'S}=\lambda_{PS}\) 推出:
\[\lambda' = \lambda-\mu t\ \ (\lambda=x,y,z,\boldsymbol{v},\boldsymbol{a},\mu=u),\ t'=t\tag{1}
\]
第二讲 狭义相对论基本假设
| 狭义相对论的相对性原理 |
|---|
| 在所有惯性系中，一切物理学定理都相同，即具有相同的数学表达式 |
| 对于描述一切物理现象的规律而言，所有惯性系都是等价的 |
- 光速不变原理
第三讲 狭义相对论的时空观
3.1 同时性的相对性
- 异地发生的两个同时事件，同时性具有相对性(对任意参考系)
- 同地发生的两个同时事件，同时性具有绝对性(对任意参考系)
3.2 时间延缓
- 时间间隔具有相对性
\[\tau=\frac{\tau_0}{\sqrt{1-(\frac{u}{c})^2}}=\gamma\tau_0\tag{2}
\]
式中，\(\gamma = \frac{1}{\sqrt{1-(\frac{u}{c})^2}}\)，\(\tau_0\) 表示同地不同时的两事件的时间间隔称为原时，且在不同参考系中测得的时间间隔以原时最短；
3.3 长度收缩
长度测量具有相对性
\[L'=L\sqrt{1-(\frac{u}{c})^2}\tag{3}
\]
式中，\(L\) 表示观测者静止时测得的长度(原长)，\(L'\) 表示在沿尺长度方向运动速度为 \(u\) 时测得的长度，且在不同参考系中测得的长度以原长最长；
第四讲 洛伦兹变换
4.1 时空坐标变换
式中，\(u\) 表示 \(S'\) 相对于 \(S\) 的速度(相对速度)，\(x'\) 表示待求坐标系中参量；
推导时间变换式: 由 \(x' = \frac{x-ut}{\sqrt{1-(\frac{u}{c})^2}}\) 及逆变换 \(x = \frac{x'+ut'}{\sqrt{1-(\frac{u}{c})^2}}\) 联立消去 \(x'\) 解 \(t'\)
4.2 时空间隔变换
4.3 爱因斯坦速度相加定律
由式 \((4)\) 求微分得:
\[dx'=\frac{(v_x-u)}{\sqrt{1-\beta^2}}dt,\ dy'= dy,\ dz'= dz,\ dt' = \frac{(1-\frac{u}{c^2}v_x)}{\sqrt{1-\beta^2}}dt
\]
\[\Rightarrow v_x'=\frac{dx'}{dt'}=\frac{v_x-u}{1-\frac{u}{c^2}v_x},\ v_y'=\frac{dy'}{dt'}=\frac{v_y\sqrt{1-\beta^2}}{1-\frac{u}{c^2}v_x},\ v_z'=\frac{dz'}{dt'}=\frac{v_z\sqrt{1-\beta^2}}{1-\frac{u}{c^2}v_x}\tag{6}
\]
第五讲 狭义相对论质点动力学
5.1 相对论动量和质量
质速关系式
\[m(v) = \frac{m_0}{\sqrt{1-(\frac{u}{c})^2}}
\]
\[\Longrightarrow \boldsymbol{p}=m\boldsymbol{v}=\frac{m_0}{\sqrt{1-(\frac{u}{c})^2}}\boldsymbol{v},\ \boldsymbol{F}=\frac{d\boldsymbol{p}}{dt}=\frac{d}{dt}(\frac{m_0}{\sqrt{1-(\frac{u}{c})^2}}\boldsymbol{v})\tag{7}
\]
式中，\(m_0\) 表示物体静止质量；
5.2 相对论动能
\[E_k = \int \boldsymbol{F}\cdot d\boldsymbol{r}=\int \frac{d(m\boldsymbol{v})}{dt}\cdot d\boldsymbol{r}=\int d(m\boldsymbol{v})\cdot \frac{d\boldsymbol{r}}{dt}=\int d(m\boldsymbol{v})\cdot\boldsymbol{v}
\]
5.3 质能方程
运动能量: \(E=mc^2\)
静止能量: \(E_0=m_0c^2\)
5.4 光子质量
- 爱因斯坦光子假说
光子能量: \(E= h\nu\)
\[\Longrightarrow m_\varphi=\frac{E}{c^2}=\frac{h\nu}{c^2}=\frac{h}{c\lambda}\tag{10}
\]
| 光子、中微子在真空中速率为\(c\)，不可能静止因此静止能量等于零 |
|---|
5.5 相对论能量与动量关系
由式 \((7)\) 得: \(m^2(1-\frac{v^2}{c^2})=m_0^2\)
第五章 量子物理基础
第一讲 普朗克量子假设
1.1 基本概念
| 热辐射 | 物体由其温度所决定的电磁辐射(温度越高，单位时间内辐射的能量越高) |
|---|---|
| 平衡热辐射 | 当辐射和吸收达到平衡时，物体的温度不再发生变化而处于热平衡状态时的热辐射 |
| 单色辐射出射度(单色辐出度) | 物体单位表面积在单位时间内发射的，波长在\(\lambda\rightarrow\lambda+d\lambda\) 范围内的辐射能 \(dM_\lambda\)与波长间隔 \(d\lambda\) 的比值 |
| 绝对黑体(黑体) | 能够全部吸收各种波长的辐射能而不发生发射和透射的物体 |
1.2 单色辐出度
\[M_\lambda(T)=\frac{dM_\lambda}{d\lambda}\tag{1}
\]
【单色辐出度图】
| 温度越高 | 单色辐出度越大，峰值波长越短 |
|---|
1.3 普朗克量子假设
\[\varepsilon=nh\nu\tag{2}
\]
式中，\(\varepsilon\) 表示腔壁中带电谐振子离散变化的能量，振子的频率为 \(\nu\)，\(n\) 表示量子数，\(h\nu\) 表示能量子——谐振子能量的最小单位(不是物质而是能量单位)；
第二讲 爱因斯坦光子理论
2.1 光电效应
| 金属及其化合物在光的照射下发射电子的现象 |
|---|
【光电效应伏安特性曲线】
| 照射光光强越大，饱和光电流越大 |
|---|
| 光电子最大初动能与照射光强度无关，而与频率成线性关系 |
2.2 光电效应方程
遏止电压: \(\frac{1}{2}mv_m^2=eU_a\)
光电效应方程: \(h\nu = A + \frac{1}{2}mv_m^2\)
截止频率: \(\nu_0=\frac{A}{h}\)
\[\Longrightarrow U_a = \frac{h}{e}\nu-\frac{A}{e}\tag{3}
\]
第三讲 康普顿效应及光子理论解释
3.1 康普顿效应
| 单色\(X\) 射线被物质散射时，散射光两种波长中有一种波长比入射线长的散射现象 |
|---|
3.2 光子理论解释
【微观机制】——等价于微观粒子的弹性碰撞
入射光子频率 \(\nu_0\),散射角为 \(\theta\) 的光子频率为 \(\nu\),电子沿着与入射线成 \(\varphi\) 角的方向运动,静质量 \(m_0\),动质量 \(m\)
由动量守恒定律得到:
由能量守恒定律得到:
第四讲 氢原子光谱 玻尔氢原子理论
4.1 氢原子光谱实验规律
氢原子光谱——线状光谱
【里德伯-里兹合并原则】
- 光谱线波数 \(\widetilde{\nu}=\frac{1}{\lambda}=T(k)-T(n)=R_H(\frac{1}{k^2}-\frac{1}{n^2})\) (\(k、n\in Z\) 且 \(n>k\))
- \(k = 1\ (n=2,3,4,\cdots)\) ——赖曼系 \(k = 2\ (n=3,4,5,\cdots)\)——巴耳末系
4.2 玻尔氢原子理论——氢原子或类氢原子
【辐射频率公式】——辐射或吸收一个频率为 \(\nu_{kn}\) 的光子
\[\nu_{kn} = \frac{|E_k-E_n|}{h}\tag{7}
\]
【角动量量子化条件】——轨道角动量不能连续变化
\[L=mvr=n\frac{h}{2\pi}=n\overline{h},\ \ n = 1,2,3,\cdots\tag{8}
\]
式中，\(\overline{h}=\frac{h}{2\pi}\) 表示约化普朗克常数；
【电子轨道半径】——电子轨道半径不能连续变化
\[m\frac{v^2}{r}=\frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}
\]
又由式 \((8)\) 得:
\[\Rightarrow r_n=n^2(\frac{\varepsilon_0h^2}{\pi me^2})=n^2r_1\ (n=1,2,3,\cdots)\tag{9}
\]
式中 \(r_1\) 表示氢原子中电子的最小轨道半径，称为玻尔半径；
\(n=1\) 的定态——基态
\(n=2,3,4,\cdots\) 各态——受激态
| 氢原子能量=电子动能+电子电势能 |
|---|
量子数为 \(n\) 的定态时氢原子能量：
\[E=\frac{1}{2}mv^2-\frac{1}{4\pi\varepsilon_0}\frac{e^2}{r}=-\frac{1}{8\pi\varepsilon_0}\frac{e^2}{r}
\]
\[\Longrightarrow E_n=-\frac{1}{8\pi\varepsilon_0}\frac{e^2}{r_n}=-\frac{1}{n^2}(\frac{me^4}{8\varepsilon_0^2h^2})\ \ \ (n=1,2,3,\cdots)\tag{10}
\]
当 \(n\rightarrow \infty\) 时,\(r_n\rightarrow \infty\)，\(\ E_n\rightarrow0\)，能级趋于连续，原子趋于电离；\(E>0\) 时，原子处于电离状态，能量可连续变化。
电离能: 使原子或分子电离所需要的能量
原子电离电势:电子使原子刚好电离所需的加速电势差
【氢原子跃迁】
高能态跃迁到低能态发射一个光子其频率和波数：
\[\nu_{nk}=\frac{E_n-E_k}{h}\ \ \ (n>k)
\]
\[\widetilde{\nu_{nk}}=\frac{1}{\lambda_{nk}}=\frac{\nu_{nk}}{c}=\frac{1}{hc}(E_n-E_k)\tag{11}
\]
常用物理常数
| 物理常数 | 物理符号 | 取值 |
|---|---|---|
| 普朗克常数 | \(h\) | \(6.62607015\times 10^{-34} \ \ J\cdot s\) |
| 电子电量 | \(e\) | \(1.6\times 10^{-19}\ \ C\) |
| 光速 | \(c\) | \(3\times 10^8\ \ m/s\) |
| 真空电容率/真空介电常量 | \(\varepsilon_0\) | \(8.85\times 10^{-12}\ \ C^2\cdot N^{-1}\cdot m^{-2}\) |