Revisiting linear regression 重新审视线性回归
课件翻译
Linear regression 线性回归
-
最经典的统计模型之一,但仍被广泛使用
-
用线性函数建模输入输出关系
\[y_{i}=\beta_1 x_{i 1}+\beta_2 x_{i 2}+\cdots+\beta_p x_{i p}+\varepsilon_i \]其中:
- \(y_{i}\) 是输出(预测目标)
- \(\boldsymbol{X}_i=\left(x_{i 1}, \ldots, x_{i p}\right)^{\top}\) 是输入向量
- \(\boldsymbol{\beta}=\left(\beta_1, \ldots, \beta_p\right)^{\top}\) 是参数(未知)
- \(\varepsilon_i\) 是一个观测噪声(随机)并假设 \(\mathbb{E}\left[\epsilon_i\right]=0\) ,\(\mathbb{V}\left[\epsilon_i\right]=\sigma^2\) 和 \(\left\{\epsilon_i\right\}_{i=1}^n\) 彼此独立(详情参见附录节)
-
从包括 \(\left(x_i, y_i\right)\) 的数据集中估算 \(\beta_i\)
例子
- y:销售量,x:产品信息
- y:燃料效率,x:引擎的设计
- y:电力消耗,x:电力消耗历史,温度
- y:毒性,x:化学成分信息
二维输入图
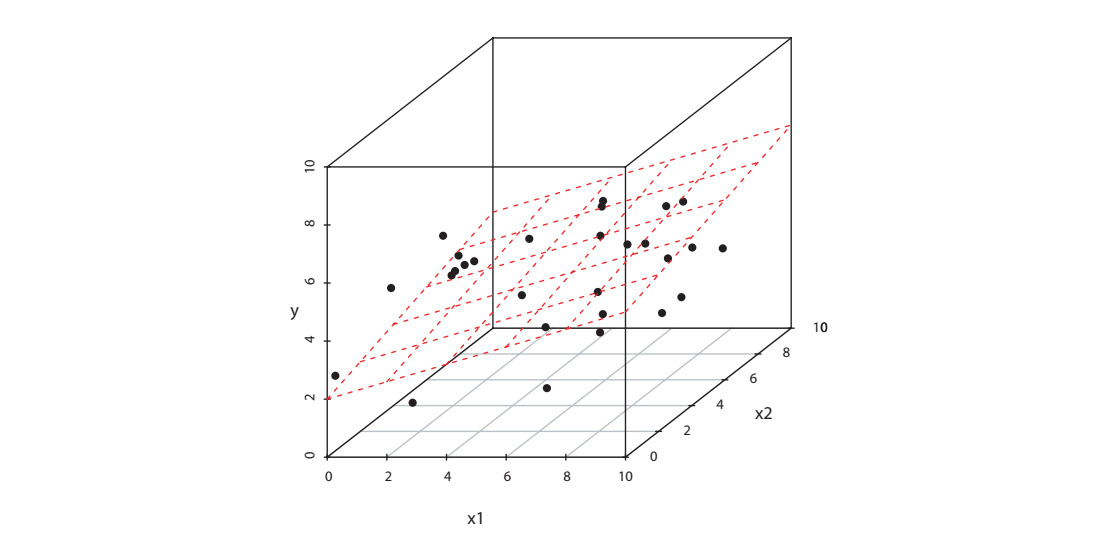
- 每个黑点都对应着 \((x_i,y_i)\)
- 红色平面表示 \(\boldsymbol{X}^{\top}\boldsymbol{\beta}\)
- 黑点和红色平面之间的差距就是 \(\varepsilon_i\)
向量矩阵符号
-
训练数据集 \(\left\{\left(x_{i},y_{i}\right)\right\}_{i=1}^{n}\)
\[\boldsymbol{X}=\left[\begin{array}{c} \boldsymbol{x}_{1}^{\top} \\ \vdots \\ \boldsymbol{x}_{n}^{\top} \end{array}\right]=\left[\begin{array}{ccc} x_{11} & \cdots & x_{1 p} \\ \vdots & & \vdots \\ x_{n 1} & \cdots & x_{n p} \end{array}\right] \in \mathbb{R}^{n \times p}, \boldsymbol{y}=\left[\begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array}\right] \in \mathbb{R}^{n} \] -
模型也可以被写成
\[\boldsymbol{y}=\boldsymbol{X}\boldsymbol{\beta}+\boldsymbol{\varepsilon} \]其中 \(\boldsymbol{\beta}=\left[\beta_{1}, \ldots, \beta_{p}\right]^{\top}\) , \(\boldsymbol{\varepsilon}=\left[\varepsilon_{1}, \ldots, \varepsilon_{n}\right]^{\top}\)
- 注意 \(\boldsymbol{y}\) 是一个随机变量,因为 \(\boldsymbol{\varepsilon}\) 是一个随机变量
- \(\mathbb{E}[\varepsilon]=\mathbf{0}\) , \(\mathbb{V}[\varepsilon]=\sigma^{2} \boldsymbol{I}\) ( \(\boldsymbol{I}\) 是单位矩阵)
Least-squares estimator (LSE) 最小二乘估计
-
误差平方和
\[\begin{aligned} \sum_{n}^{i=1} (y_i-x_i^{\top}\beta)^2 & = \begin{bmatrix}y_1-x_1^{\top}\beta&\cdots&y_n-x_n^{\top}\beta\end{bmatrix}\begin{bmatrix} y_1-x_1^{\top}\beta\\\vdots \\y_n-x_n^{\top}\beta\end{bmatrix}\\ & = (\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})^{\top}(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})\\ & = \begin{Vmatrix} \boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta} \end{Vmatrix}^{2} \end{aligned} \] -
最小二乘估计
\[\hat{\boldsymbol{\beta}} =\underset{\beta }{argmin} \begin{Vmatrix} \boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta} \end{Vmatrix}^{2} \]这是一个凸二次最小化问题,可以解析求解
Closed Form Solution of LSE 最小二乘估计的闭式解
-
取误差平方和的导数
\[\frac{\partial}{\partial \boldsymbol{\beta}}\|\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta}\|^{2} \] -
因为 \(\|\boldsymbol{y}-\boldsymbol{x} \boldsymbol{\beta}\|^{2}\) 是凸函数,最小值可以通过将导数设置为0来确定
\[\begin{aligned} \frac{\partial}{\partial \boldsymbol{\beta}}\|\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta}\|^{2} & = \frac{\partial}{\partial \boldsymbol{\beta}}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta})^{\top}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta})\\ & = \frac{\partial}{\partial \boldsymbol{\beta}}(\boldsymbol{y}^{\top }\boldsymbol{y}-\boldsymbol{y}^{\top }\boldsymbol{X}\boldsymbol{\beta}-(\boldsymbol{X}\boldsymbol{\beta})^{\top}\boldsymbol{y}-(\boldsymbol{X}\boldsymbol{\beta})^{\top}(\boldsymbol{X}\boldsymbol{\beta})) \end{aligned} \]其中
\[\begin{aligned} (\boldsymbol{X}\boldsymbol{\beta})^{\top}\boldsymbol{y} & = \boldsymbol{\beta}^{\top}\boldsymbol{X}^{\top}\boldsymbol{y}\\ \boldsymbol{y}^{\top}\boldsymbol{X}\boldsymbol{\beta} & = \boldsymbol{\beta}^{\top}(\boldsymbol{y}^{\top}\boldsymbol{X})^{\top}\\ & = \boldsymbol{\beta}^{\top}\boldsymbol{X}^{\top}\boldsymbol{y} \end{aligned} \]故
\[\begin{aligned} \frac{\partial}{\partial \boldsymbol{\beta}}\|\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta}\|^{2} & = \frac{\partial}{\partial \boldsymbol{\beta}}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta})^{\top}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\beta})\\ & = \frac{\partial}{\partial \boldsymbol{\beta}}(\boldsymbol{y}^{\top }\boldsymbol{y}-\boldsymbol{y}^{\top }\boldsymbol{X}\boldsymbol{\beta}-(\boldsymbol{X}\boldsymbol{\beta})^{\top}\boldsymbol{y}-(\boldsymbol{X}\boldsymbol{\beta})^{\top}(\boldsymbol{X}\boldsymbol{\beta}))\\ & = \frac{\partial}{\partial \boldsymbol{\beta}}(\boldsymbol{y}^{\top }\boldsymbol{y}-2\boldsymbol{\beta}^{\top}\boldsymbol{X}^{\top}\boldsymbol{y}-(\boldsymbol{X}\boldsymbol{\beta})^{\top}(\boldsymbol{X}\boldsymbol{\beta}))\\ & = -2\boldsymbol{X}^{\top}\boldsymbol{y}+2\boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{\beta} \end{aligned} \]令
\[\begin{aligned} -2\boldsymbol{X}^{\top}\boldsymbol{y}+2\boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{\beta} & = 0 \end{aligned} \]\[\begin{aligned} \boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{\beta} & = \boldsymbol{X}^{\top}\boldsymbol{y} \end{aligned} \]假设 \((\boldsymbol{x}^{\top}\boldsymbol{x})^{-1}\) 存在,我们得到LSE为
\[\hat{\boldsymbol{\beta}}=(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y} \]即正规方程
Estimation Bias and Variance 估计偏差和方差
-
当 \(\boldsymbol{y}\) 是随机的, \(\hat{\boldsymbol{\beta}}=(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y}\) 也是随机的
对具有随机性的数据进行的估计也包含随机性
-
\(\hat{\boldsymbol{\beta}}\) 遵循一些分布,从中我们只能获得一个使用给定数据集计算的实现
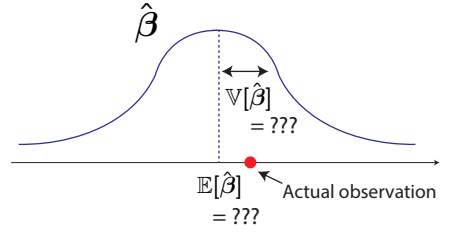
因为 \(\mathbb{E}[\boldsymbol{y}]=\mathbb{E}[\boldsymbol{X} \boldsymbol{\beta}+\varepsilon]=\boldsymbol{X} \boldsymbol{\beta}\) ,有
\[\begin{aligned} \mathbb{E}[\boldsymbol{\hat{\beta}}] & = \mathbb{E}[(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y}]\\ & = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\mathbb{E}[\boldsymbol{y}]\\ & = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{X}\boldsymbol{\beta} \end{aligned} \]因为
\[(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{X}=\boldsymbol{I} \]故
\[\mathbb{E}[\boldsymbol{\hat{\beta}}] = \boldsymbol{\beta} \]因为当 \(\boldsymbol{M}\) 为常数矩阵且 \(\boldsymbol{a}\) 为随机向量时,有
\[\mathbb{V}[\boldsymbol{M} \boldsymbol{a}]=\boldsymbol{M} \mathbb{V}[\boldsymbol{a}] \boldsymbol{M}^{\top} \]且 \(\mathbb{V}[\varepsilon]=\sigma^{2} \boldsymbol{I}\) 故
\[\begin{aligned} \mathbb{V}[\boldsymbol{\hat{\beta}}] & = \mathbb{V}[(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y}]\\ & = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\mathbb{V}[\boldsymbol{y}]\boldsymbol{X}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\sigma^{2} \boldsymbol{I}\boldsymbol{X}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = \sigma^{2}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{X}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = \sigma^{2}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1} \end{aligned} \] -
这种分布的性质在统计学中得到了广泛的研究,因为它有助于讨论LSE的优势(在假设检验中也很有用,尽管本课没有讨论它)
- 在这里,我们考虑的是 \(\hat{\beta}\)
-
Estimation Bias and Estimation Variance 估计偏差和估计方差
上边一节已经推导过了
- \(\hat{\beta}\) 被称作无偏估计量
- 估计方差的方程有助于评估估计器的不确定性
- 高斯-马尔可夫定理(详情见附录)
- LSE在所有无偏线性估计器中具有最小的估计方差,由此LSE被称为best linear unbiased estimator最佳线性无偏估计器(BLUE)
附录
范数
有 \(\boldsymbol{a}=\left(a_{1}, \ldots, a_{n}\right)^{\top}\) 时范数为
向量求导
一般来说,对于函数f相对于向量 \(\boldsymbol{v}=\left(v_{1}, \ldots, v_{n}\right)\)
对于常用的向量求导,参见Matrix Cookbook 2.4
期望与方差
-
对于连续的随机变量 \(x\in \mathbb{R}\)
\[\mathbb{E}[x]=\int_{x} x p(x) \mathrm{d} x \]如果x是离散变量 \(x\in \mathcal{X}\) , \(\mathcal{X}\) 是一组候选值
\[\mathbb{E}[x]=\sum_{x \in \mathcal{X}} x p(x) \] -
方差
\[\mathbb{V}[x]=\mathbb{E}\left[(x-\mathbb{E}[x])^{2}\right] \]两个随机变量x和y的协方差为
\[\operatorname{Cov}(x, y)=\mathbb{E}[(x-\mathbb{E}[x])(y-\mathbb{E}[y])] \]
期望与协方差矩阵
-
\(\mathbb{E}\) 表示随机变量的期望值,对于随机变量的向量 \(\boldsymbol{a}=\left(a_{1}, \ldots, a_{n}\right)^{\top}\) ,有
\[\mathbb{E}[\boldsymbol{a}]=\left[\begin{array}{c} \mathbb{E}\left[a_{1}\right] \\ \vdots \\ \mathbb{E}\left[a_{n}\right] \end{array}\right] \] -
对于随机变量的向量 \(\boldsymbol{a}=\left(a_{1}, \ldots, a_{n}\right)^{\top}\) ,协方差 \(\mathbb{V}[\mathbf{a}]\) 为
\[\mathbb{V}[\mathbf{a}]=\mathbb{E}\left[(\mathbf{a}-\mathbb{E}[\mathbf{a}])(\boldsymbol{a}-\mathbb{E}[\mathbf{a}])^{\top}\right] \]注意, \(\mathbb{V}[\mathbf{a}]\) 的 \(i\) , \(j\) 元素对应于协方差\(a_i\)和\(a_j\)的
例如, \(\operatorname{Cov}\left(a_{i}, a_{j}\right)=\mathbb{E}\left[\left(a_{i}-\mathbb{E}\left[a_{i}\right]\right)\left(a_{j}-\mathbb{E}\left[a_{j}\right]\right)\right]\)
线性变换向量的协方差矩阵
当 \(\boldsymbol{M}\) 为常数矩阵且 \(\boldsymbol{a}\) 为随机向量时,有
这可以通过 \(\mathbb{V}\) 的定义来证明
矩阵的不等式
-
矩阵 \(\boldsymbol{M}\) 的不等式
\[\boldsymbol{M}≥0 \]将其表示为半正定矩阵
\[\boldsymbol{x}^{\top}\boldsymbol{M}\boldsymbol{x}≥0 \]对于 \(\forall\boldsymbol{x}\) 等价地, \(\boldsymbol{M}\) 的所有特征值都是非负的
-
那么, \(\boldsymbol{A}≥\boldsymbol{B}\) 表示 \(\boldsymbol{A}-\boldsymbol{B}≥0\) ,这意味着 \(\boldsymbol{A}-\boldsymbol{B}\) 是半正定的
高斯-马尔可夫定理
-
假设一个矩阵 \(\boldsymbol{C}\in \mathbb{R}^{p×n}\) 满足
\[\boldsymbol{\beta} = \mathbb{E}[\boldsymbol{C}\boldsymbol{y}] \]- \(\boldsymbol{C}\boldsymbol{y}\) 称为无偏线性估计量,因为它是 \(\boldsymbol{y}\) 的无偏线性变换
- 当 \(\boldsymbol{C}=(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\) 时, \(\boldsymbol{C}\boldsymbol{y}\) 为LSE
- 当 \(\boldsymbol{\beta}=\mathbb{E}[\boldsymbol{C}(\boldsymbol{X} \boldsymbol{\beta}+\varepsilon)] \Rightarrow \boldsymbol{\beta}=\boldsymbol{C} \boldsymbol{X} \boldsymbol{\beta} \Rightarrow \mathbf{I}=\boldsymbol{C} \boldsymbol{X}\) 时,任何满足 \(\mathbf{I}=\boldsymbol{C} \boldsymbol{X}\) 的 \(\boldsymbol{C}\) 都会变成无偏(并且可以存在)
-
高斯-马尔可夫定理保证(省略证明)
\[\mathbb{V}[\hat{\boldsymbol{\beta}}] \leq \mathbb{V}[\boldsymbol{C y}] \]
习题
Exercise 0: Short Quiz
在适当的假设下,最小二乘估计量的期望值等于真实值。通常,具有这种性质的估计量称为[(A)]估计量。什么是[(A)]?
- 无偏估计量
Exercise 1
证明 \(\mathbb{V}[\boldsymbol{\hat{\beta}}] = \sigma^{2}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\)
- 上边已经证明过了\[\begin{aligned} \mathbb{V}[\boldsymbol{\hat{\beta}}] & = \mathbb{V}[(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{y}]\\ & = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\mathbb{V}[\boldsymbol{y}]\boldsymbol{X}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = (\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\sigma^{2} \boldsymbol{I}\boldsymbol{X}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = \sigma^{2}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\boldsymbol{X}^{\top}\boldsymbol{X}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = \sigma^{2}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1} \end{aligned} \]
Exercise 2
令
假设 \(\mathbf{X}\) 满足
-
每个维度的平均值为零:
\(\bar{x}_{j}=\frac{1}{n} \sum_{i=1}^{n} x_{i j}=0(\text { for } j=1,2)\)
-
每个维度的方差为一:
\(\frac{1}{n} \sum_{i=1}^{n}\left(x_{i j}-\bar{x}_{j}\right)^{2}=\frac{1}{n} \sum_{i=1}^{n} x_{i j}^{2}=1(\text { for } j=1,2)\)
-
两个维度的协方差为零:
\(\frac{1}{n} \sum_{i=1}^{n}\left(x_{i 1}-\bar{x}_{1}\right)\left(x_{i 2}-\bar{x}_{2}\right)=\frac{1}{n} \sum_{i=1}^{n} x_{i 1} x_{i 2}=0\)
写出 \(\mathbb{V}[\boldsymbol{\hat{\beta}}]\)
-
\[\begin{aligned} \mathbb{V}[\boldsymbol{\hat{\beta}}] & = \sigma^{2}(\boldsymbol{X}^{\top}\boldsymbol{X})^{-1}\\ & = \sigma^{2}(\left[\begin{array}{cc} x_{11} & \cdots & x_{n1} \\ x_{12} & \cdots & x_{n 2} \end{array}\right]\left[\begin{array}{cc} x_{11} & x_{12} \\ \vdots & \vdots \\ x_{n 2} & x_{n 2} \end{array}\right])^{-1}\\ & = \sigma^{2}\left[\begin{array}{cc} \sum_{i=1}^{n} x_{i2}^2 & \sum_{i=1}^{n} x_{i1}x_{i2}\\ \sum_{i=1}^{n} x_{i1}x_{i2} & \sum_{i=1}^{n} x_{i2}^2 \end{array}\right]^{-1}\\ & = \sigma^{2}\left[\begin{array}{cc} n & 0\\ 0 & n \end{array}\right]^{-1}\\ & = \sigma^{2}\left[\begin{array}{cc} \frac{1}{n} & 0\\ 0 & \frac{1}{n} \end{array}\right]\\ \end{aligned} \]