2023-06-18《计算方法》- 陈丽娟 - 方程的近似解法
在这里我先跳过了曲线拟合这一部分,这是因为我主要想快速切入到数值微积分部分,因此直接直接来到了方程的近似解部分。
一、二分法
二分法对如下问题进行求解:
设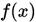 在区间
在区间 上连续,且
上连续,且 ,求
,求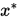 使得
使得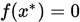 .
.
这里给出一个可调整的二分法算法:
- 给定参数
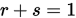 ,
, 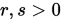 ;
; - 在区间
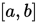 内取一点
内取一点 , 可知
, 可知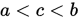 ;
; - 计算
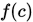 , 若
, 若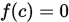 (
( ), 则
), 则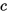 是解;
是解; - 若
 , 则令
, 则令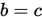 , 否则
, 否则 ;
; - 回到第2步。
这个算法含有可调节参数 , 其取值对逼近速度将产生影响,当
, 其取值对逼近速度将产生影响,当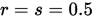 就是二分法。另外这里的二分法适用于一维情况(多维情况怎么做尚不清楚,没有搜索到,如知道请告知,谢谢)
就是二分法。另外这里的二分法适用于一维情况(多维情况怎么做尚不清楚,没有搜索到,如知道请告知,谢谢)
下面给出这个算法的对应程序(黄金比例):
- % r分法求解函数f在ab上的根,精度为epsilon
- function [xs xslog] = BiSection(f, a, b, r, epsilon)
- xslog = [];
- fa = feval(f, a);
- fb = feval(f, b);
- if abs(fa) <= epsilon
- xs = a;
- elseif abs(fb) <= epsilon
- xs = b;
- elseif fa * fb > 0
- xs = Inf;
- else
- while fa * fb < 0
- c = r*a + (1-r) * b;
- xslog = [xslog c];
- fc = feval(f, c);
- if abs(fc) <= epsilon
- xs = c;
- break
- else
- if fa * fc < 0
- b = c;
- else
- a = c;
- end
- end
- end
- end
- end
对应的测试用例
- % 二分法测试用例
- f = @(x) sin(x);
- r = 0.618;
- epsilon = 1e-8;
- %f(a) f(b) > 0
- a = 0.1;
- b = pi/2;
- [xs xslog] = BiSection(f, a, b, r, epsilon);
- %f(a) = 0
- a = 0;
- b = pi/2;
- [xs xslog] = BiSection(f, a, b, r, epsilon);
- %f(b) = 0
- a = 0.1;
- b = pi;
- [xs xslog] = BiSection(f, a, b, r, epsilon);
- % f(a)f(b)<0
- a = 0.3;
- b = 5;
- [xs xslog] = BiSection(f, a, b, r, epsilon);
- r = 0.5;
- [xs1 xslog1] = BiSection(f, a, b, r, epsilon);
- r = 0.7;
- [xs2 xslog2] = BiSection(f, a, b, r, epsilon);
- plot(xslog)
- hold on
- plot(xslog1)
- hold on
- plot(xslog2)
- legend(["0.3" "0.5" "0.7"])

enter description here
二、迭代法基本思想
对于求解 ,该式等价于
,该式等价于
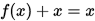
令
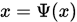 , 得到迭代格式
, 得到迭代格式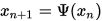
若
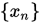 收敛, 则有
收敛, 则有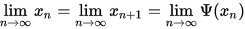
即
 ,也即是
,也即是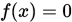 .
.不动点迭代法对于很多零点(不动点)问题都行之有效,但是基本的迭代格式要求
 满足一定的条件(非扩张映射),这部分可以参考不动点理论,这里给几个基本的不动点相关论文:
满足一定的条件(非扩张映射),这部分可以参考不动点理论,这里给几个基本的不动点相关论文:Xu H. Iterative Algorithms for Nonlinear Operators. Journal of the London Mathematical Society. 2002;66:240-56. doi: 10.1112/S0024610702003332.
Maingé P-E. Strong Convergence of Projected Subgradient Methods for Nonsmooth and Nonstrictly Convex Minimization. Set-Valued Analysis. 2008;16(7):899-912. doi: 10.1007/s11228-008-0102-z.
注:在构建迭代序列的时候,特别应该注意到构造的算子 尽量满足非扩张性(1-Lipschitiz连续)
尽量满足非扩张性(1-Lipschitiz连续)
- 定理1
- 如果
 满足下列条件:
满足下列条件:
- 当
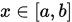 时,
时, ;
; - 当任意
 时,存在
时,存在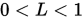 , 使
, 使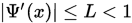 ,
,
则方程 在
在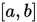 上有唯一的根
上有唯一的根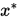 , 且对任意的
, 且对任意的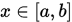 ,有:
,有: - 迭代公式
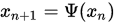 收敛于
收敛于 ;
; - 有误差估计式
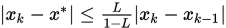 ;
; 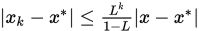
上述定理的证明由拉格朗日定理和迭代格式立即可得。
书中的局部收敛性和收敛速度这里不做讨论。
三、牛顿法
对函数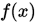 在
在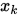 处做泰勒展开可得
处做泰勒展开可得
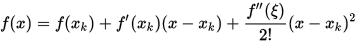
令
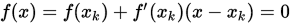 可以得到近似的不动点迭代格式
可以得到近似的不动点迭代格式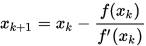
上述形式即牛顿迭代法。注意到一开始我们是使用的泰勒展开得到的,而一阶泰勒展开仅在很小的邻域内有较好的近似结果,因此牛顿法仅适用于初始点在零点附近处使用。为了能够得到对任意点均能收敛的牛顿迭代法,可以使用牛顿下山法
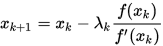
其中
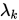 取值为
取值为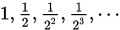 使得
使得 .
.这里我们给出程序:
- % f目标函数, x0初始点,epsilon, 用于求导的h
- function [xs, xslog] = NewtonDes(f, x0, epsilon, h, maxit)
- xs = x0;
- iter = 1;
- xslog = [];
- if abs(feval(f,x0)) <= epsilon
- else
- while abs(feval(f,xs)) > epsilon
- if iter > maxit
- break
- end
- x0 = xs;
- lambda = 1;
- fx0 = feval(f,x0);
- fxdiff = (feval(f,x0+h) - fx0)/ h;
- xs = x0 - lambda * fx0 / fxdiff;
- while abs(feval(f,xs)) > abs(fx0)
- lambda = lambda / 2;
- xs = x0 - lambda * fx0 / fxdiff;
- end
- xslog = [xslog xs];
- iter = iter + 1;
- end
- end
- end
例子
- f = @(x) 5 .* x.^3+x.^2-x+1;
- epsilon = 1e-8;
- x0 = 0.4;
- h = 1e-4;
- maxit = 1e3;
- [xs, xslog] = NewtonDes(f, x0, epsilon, h, maxit)
得到解为-0.7824。注意这里我们设置导数的计算间隔为 , 当间隔取得很小的时候,上述程序会有数值稳定性问题:
, 当间隔取得很小的时候,上述程序会有数值稳定性问题:
- f = @(x) 5 .* x.^3+x.^2-x+1;
- epsilon = 1e-8;
- x0 = 0.4;
- h = 1e-8;
- maxit = 1e3;
- [xs, xslog] = NewtonDes(f, x0, epsilon, h, maxit)
通过断点,这个问题来自于
- fxdiff = (feval(f,x0+h) - fx0)/ h;
- xs = x0 - lambda * fx0 / fxdiff;
由于这个函数本身中间部分很平滑,导致了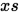 很大(2333), 然后又需要重新从2333开始通过lambda逼近到更好的解。然后又由于
很大(2333), 然后又需要重新从2333开始通过lambda逼近到更好的解。然后又由于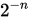 指数下降,导致最后几乎在一个非零解的地方不动。这个问题可以通过更换初始值得到缓解:
指数下降,导致最后几乎在一个非零解的地方不动。这个问题可以通过更换初始值得到缓解:
- f = @(x) 5 .* x.^3+x.^2-x+1;
- epsilon = 1e-8;
- x0 = -0.4;
- h = 1e-8;
- maxit = 1e3;
- [xs, xslog] = NewtonDes(f, x0, epsilon, h, maxit)
另外可以给出一个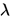 不重置的算法:
不重置的算法:
- % f目标函数, x0初始点,epsilon, 用于求导的h
- function [xs, xslog] = NewtonDes(f, x0, epsilon, h, maxit)
- xs = x0;
- iter = 1;
- xslog = [];
- lambda = 1;
- if abs(feval(f,x0)) <= epsilon
- else
- while abs(feval(f,xs)) > epsilon
- if iter > maxit
- break
- end
- x0 = xs;
- fx0 = feval(f,x0);
- fxdiff = (feval(f,x0+h) - fx0)/ h;
- xs = x0 - lambda * fx0 / fxdiff;
- while abs(feval(f,xs)) > abs(fx0)
- lambda = lambda / 2;
- xs = x0 - lambda * fx0 / fxdiff;
- end
- xslog = [xslog xs];
- iter = iter + 1;
- end
- end
- end
这个算法也可以逼近解,但是同样会存在对某些初始值在导数间隔很小的时候不能逼近到解。书中并未给出如何解决这个问题,因此高精度的牛顿下山法我并未实现。(希望书后面的数值微积分中能有更好的处理导数的方法)