Learning Semi-supervised Gaussian Mixture Models for Generalized Category Discovery
Abstract
在本文中,我们解决了广义类别发现(generalized category discovery, GCD)的问题,即给定一组图像,其中一部分被标记,其余部分未标记,任务是利用来自有标签数据的信息,在无标签数据中自动聚类图像,而无标签数据包含来自标记类的图像和新图像。
Introduction
Semi-supervised learning (SSL) 被提出作为在有标签数据和无标签数据上学习模型的解决方案。但是,SSL假定无标签数据中的所有对象类都已经提供了标记实例。
novel category discovery (NCD) 通过转移从已知类的标记实例中学习到的知识来自动发现新类,假设无标签数据仅包含来自新类的实例。
Generalized category discovery (GCD) 进一步放宽了NCD中的假设,并处理了一个更广义的设置,其中未标记的数据包含已知和新类别的实例。现有方法假设类数是已知的先验或预先计算好的。
在本文中,我们认为表征学习和类数估计应该一起考虑,并且可以相互加强,即好的表征可以帮助更准确地估计类数,准确的类数可以帮助学习更好的特征表示。
为此,我们提出了一个统一的类似EM算法的框架,在特征表示学习和类数估计之间交替进行,其中E步旨在自动估计无标签数据中的适当类数和类的原型,M步旨在利用估计的类数和类原型学习更好的表示。
贡献点:
- 我们证明了在广义类别发现中,类数估计和表示学习在学习过程中是相互加强的。好的表示可以给出更好的类数估计,反之亦然。
- 我们提出了一个类似EM的框架,它在基于GMM变体的原型估计(E -步)和基于原型对比学习的表示学习(M -步)之间交替进行。
- 我们引入了GMM的半监督变体,该变体具有随机分裂和合并机制,通过基于Metropolis-Hastings比率的聚类紧密性和可分离性检验,允许原型的动态变化。
- SOTA
related work
Novel category discovery
列举了NCD的方法,然后扩展到GCD上。提出大多数方法仍然假设新的类数是先验已知的,这在现实世界中往往不是这样,在本文中,我们证明了类数估计和表示学习可以共同考虑,以相互受益。
Contrastive learning
该方法中,原型被视为集群中心,它可以在GCD的部分监督设置中进行表示学习,以更好地适应将数据划分到不同集群的GCD任务。
Unsupervised clustering
最近,DeepDPM[37]通过采用类似的拆分/合并框架,改变推断的聚类数量,自动确定给定数据集的聚类数量。然而,由于这些方法的无监督性质,对于如何形成聚类没有先验知识或监督,因此可以产生遵循不同聚类标准的多个相同有效的聚类结果。我们希望模型使用由有标签数据隐式给出的唯一聚类标准。
Method
给定一个带有部分标记的数据的集合 \(\mathcal{D}=\mathcal{D}^l \cup \mathcal{D}^u\),其中 $\mathcal D^l= {(x_i,y_i^l) } \in \mathcal{X} \times \mathcal{Y}_l $ 是有标签数据,$\mathcal D^u= {(x_i,y_i^u) } \in \mathcal{X} \times \mathcal{Y}_u $ 是无标签数据,且 \(\mathcal{Y}_l \sub \mathcal{Y}_u\)。广义类别发现(GCD)旨在通过转移从 \(\mathcal{D}^l\) 中获得的知识,为 \(\mathcal{D}^u\) 中未标记的实例自动分配标签。
设 \(\mathcal{D}^l\) 中的类别个数为 \(K^l=|\mathcal{Y}_l|\) , \(\mathcal{D}^u\) 中的类别个数为 \(K^u =|\mathcal{Y}^u|\)。则新类别数 \(\mathcal{D}^u\) 为 \(K^n = |\mathcal{Y}^u \backslash \mathcal{Y}^l | = Ku−Kl\)。虽然 \(K^l\) 可以从标记的数据中获得,但我们不假设 \(K^n\) 或 \(K^u\) 是已知的。这是一个反映真实开放世界的现实设置,我们经常可以访问一些有标签数据,但在无标签数据中,我们也有来自未见过的新类别的实例。
GCD的主要挑战是表示学习、类别数量估计和标签分配。现有的NCD和GCD方法[16,43]分别处理这三个挑战。然而,我们相信它们彼此之间有着内在的联系。标签分配取决于表征和类别数量估计。一个好的类数估计可以促进表征学习,从而更好地分配标签,反之亦然。因此,在本文中,我们的目标是共同应对学习过程中的这些挑战,以获得更可靠的GCD。
我们提出了一个统一的类似EM的框架,该框架在表示学习和类数估计之间交替进行,而标签分配则是类数估计过程中的副产品。
在E步中,我们引入高斯混合模型(GMM)的半监督变体,基于当前学习的表征,动态拆分、合并簇,从而估计类数,形成一组seen类和unseen类的类原型。
在M步中,我们使用从E步得到的聚类中心,通过原型对比学习来训练模型产生判别表示。
训练后,每个实例可以通过简单地识别最近的原型来进行分类。
Representation learning
对比学习公式
原型对比学习使用一组原型 \(\mathcal{C}=\{\mu_1,\dots,\mu_K\}\) 来学习表征 \(z_i=f(x_i) \in \mathbb{R}^d\)。
其中 \(\mu_s\) 是\(z_i\) 所对应的原型。在我们的例子中,原型可以被解释为每个类的类中心。为了==获得 seen类别的原型,我们直接通过平均有标签实例的特征向量来计算类均值。对于unseen类别,我们使用高斯混合模型(GMM)的半监督变体获得原型,将在第3.2节中介绍。这样,通过找到最近的原型,可以很容易地实现对未标记图像的簇分配。==
我们观察到,只有少数几个主要维度已经可以恢复 \(z_i\) 的表示空间中的大部分方差,这被称为维度坍缩(dimensional collapse,DC)。为了减轻表征学习中的DC,我们将PCA应用于一个矩阵 \(Z\) 上,该矩阵 \(Z\) 由一组小批特征 \(z_i\) 组成,批大小为 \(n\),特征维数为\(d\),有效主方向数为\(q\)。因此得到 \(Z \approx U diag(S) V^T\),其中 \(U \in \mathbb{R}^{n \times q},S \in \mathbb{R}^q,V\in\mathbb{R}^{d \times q}\)。我们将 \(z_i\) 投影到主方向上,得到一个更紧凑的特征 \(v_i = V \cdot z_i\),并将PCL的 Eq.(2) 中的特征 \(z_i\) 替换为 \(v_i\)。原型也在投影空间中计算。
联合使用自监督对比学习和PCL来训练我们的模型
其中 \(\lambda(t)\) 是一个线性warmup函数,定义为 \(\lambda(t)=min(1,\frac{t}{T})\),其中 \(t\) 是当epoch,T是warmup的长度(在我们的实验中 \(T = 20\))。这是因为在开始时,表征不适合聚类,因此获得的原型不具有促进表示学习的信息。
Class number and prototypes estimation with semi-supervised Gaussian mixture model
其中 \(\mathcal{N}(z|\mu,\Sigma_i)\) 为高斯概率密度函数,其中均值为 \(\mu_i \in \mathbb{R}^d\),方差为 \(\Sigma_i \in \mathbb{R}^{d\times d}\),\(\pi_i\) 为第 \(i\) 个高斯混合的权重, \(\sum_{i=1}^N \pi_i = 1\)。
为了估计未知类数 \(K^u\),我们在建模过程中采用自动分割合并策略,从而得到最优 \(K\),使它尽可能接近 \(K^u\)。对于初始化,\(K\) 可以设置为大于 \(K_l\) 的任何数字。在我们的实验中,我们简单地将组件的初始数量设置为默认的 \(K_{init}=K^l+\frac{K^l}{2}\)
我们使用 \(k=K\) 的半监督k-means算法来获得混合模型中每个成分的 \(\mu\) 和 \(\Sigma\)。半监督k-means算法对于来自同一类的有标签实例,将其分配到同一集群;来自不同类的有标签实例不会被分配到同一集群。为了便于拆分和合并,对于每一个由 \(\mu_i\) 和 \(\Sigma_i\) 定义的高斯分量,我们运行 \(k = 2\) 的 k-means,得到 \(\mu_{i,1},\mu_{i,2},\Sigma_{i,1},\Sigma_{i,2}\),然后用具有两个子分量 \(\mu_{i,1},\mu_{i,2},\Sigma_{i,1},\Sigma_{i,2},\pi_{i,1}+\pi_{i,2}=1\)的的GMM来描述它。
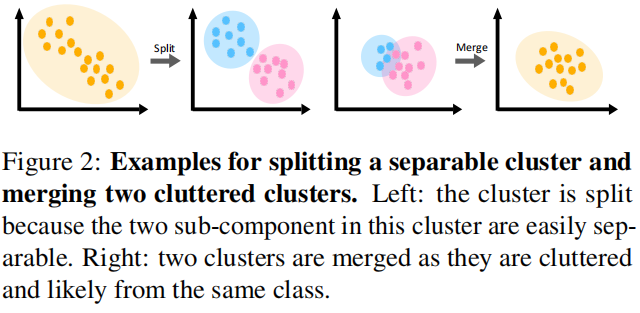
我们使用Metropolis-Hastings框架计算将集群随机分成两个的概率 \(p_s=\min(1, H_s)\) 。Hastings ratio定义为
其中,\(\Gamma\) 是阶乘函数,即,\(\Gamma(n) = n! = n \times (n - 1) \times \cdots \times 1\),\(\mathcal{Z}_i\) 是聚类 \(i\) 中的数据点集合,\(\mathcal{Z}_{i, j}\) 是聚类 \(i\) 中第 \(j\) 个子聚类的数据点集合,\(N_i = |\mathcal{Z}_i|\),\(N_{i, j} = |\mathcal{Z}_{i, j}|\),\(h(Z ; \theta)\) 是通过在高斯分布中积分出 \(\mu\) 和 \(\Sigma\) 参数后观察数据 \(\mathcal{Z}\) 的边际似然性,\(\theta\) 是 \(\mu\) 和 \(\Sigma\) 的先验分布。
这个 \(H_s\) 背后的直觉是,如果两个子组件中的数据点数量大致平衡(由 \(\Gamma(\cdot)\) 度量),两个子分量中的数据点是相互独立的(由 \(h(\cdot;\theta)\) 度量),则更应该将两个子分量分开。在执行拆分操作后,以前组件\(i\)的 \(\mu_i\) 和 \(\Sigma_i\) 将被替换为两个子组件中的 \(\mu_{i,1},\mu_{i,2},\Sigma_{i,1},\Sigma_{i,2}\)。当一个拆分结束后,我们将在两个新形成的组件中运行两个k-means来获得它们对应的子组件。
相反,如果两个集群相互混杂,则应该合并它们。与分割类似,我们通过 \(p_m=\min(1,H_m)\) 确定合并概率,其中 \(H_m\) 的计算方法如下:
注意,\(H_s\) 和 \(H_m\) 都在 \((0,+\infty)\) 的范围内,因此我们使用 \(p_s = \min(1, H_s)\) 和 \(p_m = \min(1, H_m)\) 将其转换为有效概率。
为了在拆分合并过程中考虑到有标签的实例,如果一个集群由有标签的实例组成,我们设置它的 \(p_s=0\);对于两个集群,如果包含来自两个不同标签的实例,我们设置它们的 \(P_m = 0\)。
在拆分和合并过程中,我们首先根据 \(p_s\) 进行拆分,然后根据 \(p_m\) 进行合并。通过拆分新形成的簇将不会在合并步骤中被重用。
pseudo-code

Experimental results
Experimental setup
在 通用图像分类基准 和 最近提出的语义转换基准 上做实验。数据划分如下:
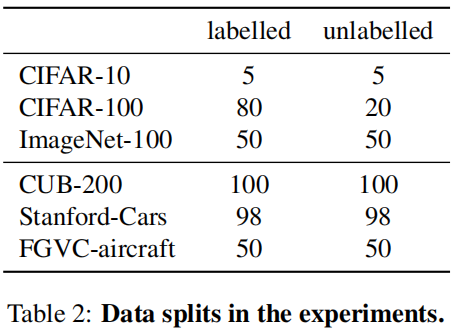
使用clustering accuracy (ACC) 进行评价。\(ACC=\frac{1}{M}\sum_{i=1}^M\mathbb{1}(y_i^*=g(\hat y_i))\)。其中 \(y^*\) 为真实标签,\(\hat y\) 为模型预测的聚类分配,\(g\) 将预测的聚类分配 \(\hat y\) 匹配到实际的类标签 \(y^*_i\) 的最优排列,\(M=|\mathcal{D}^u|\)
Comparison with the state-of-the-art
从第6行vs第7行,第10行vs第11行,我们可以看到,额外的PCA层可以有效地提高性能,而且PCA在“新”类上的性能改进比在“旧”类上的性能改进更大,这验证了PCA可以防止表示空间崩溃,并在不使用任何标签的情况下提高类的性能。
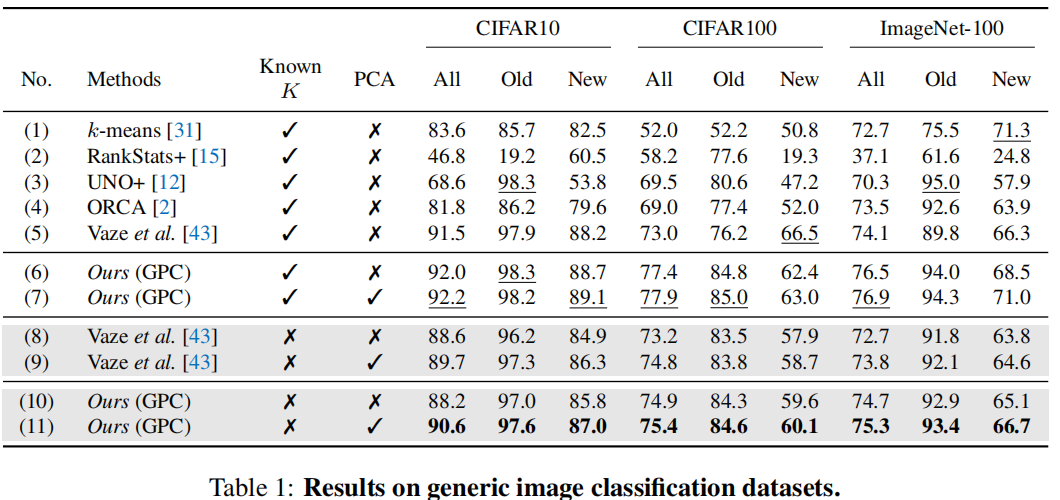
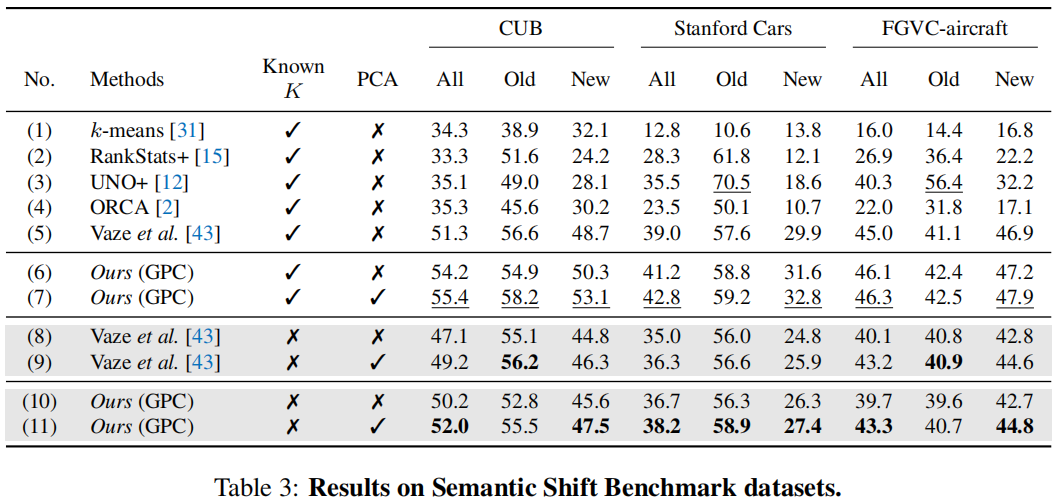
Novel class number estimation
我们验证了初始猜测\(K_{init}\) 的不同选择对估计的类数的影响。如表4所示,其中 \(K_{init}^n=K_{init}-K^l\) 。
我们发现 \(K_{init}=K^l+\frac{K^l}{2}\) 是一个简单而可靠的选择。

Ablation study
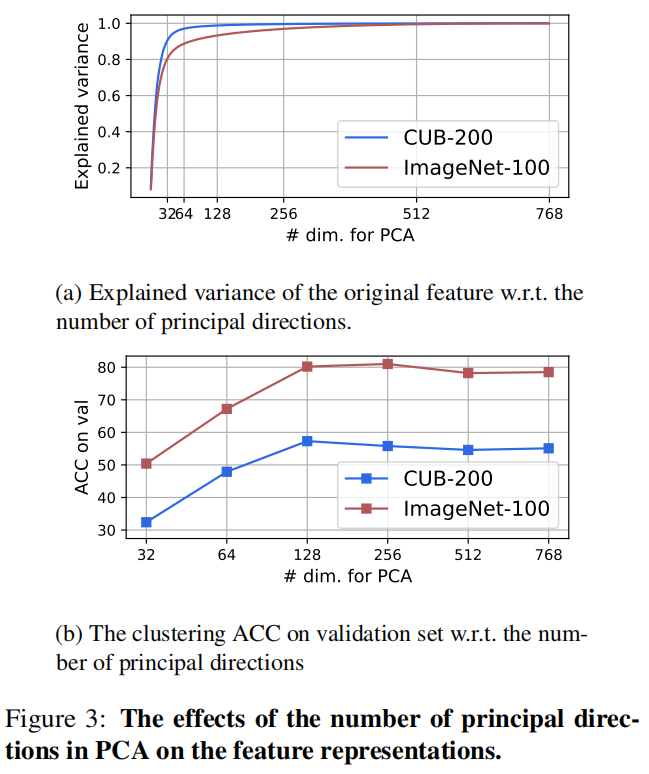
Number of dimensions in PCA
128个主方向已经可以解释数据中的大部分方差,且效果已经足够好,因此我们选择所有实验的PCA维数为128。
Different methods for prototype estimation
半监督gmm最好
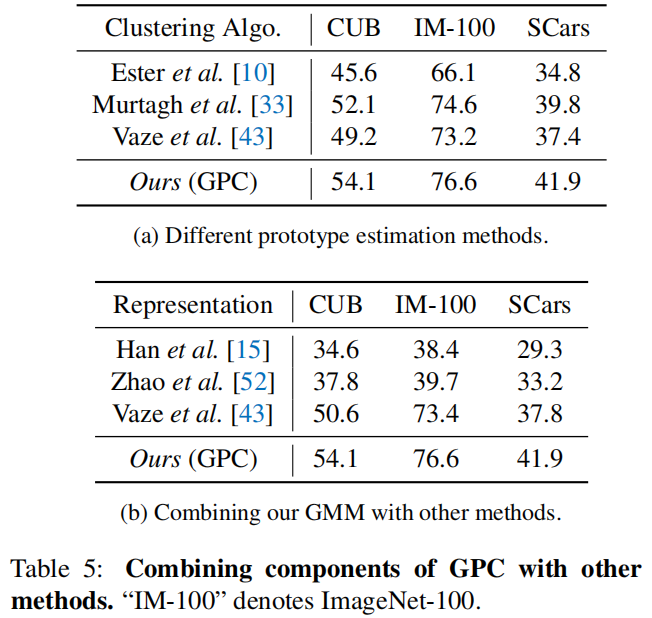
Combining our GMM with other GCD methods
与表1和表3中的第9行相比,我们可以看到使用我们的GMM也可以在CUB和Stanford Cars上得到改善[43],而我们提出的框架在所有数据集上都能始终取得更好的性能,再次验证了我们的设计选择
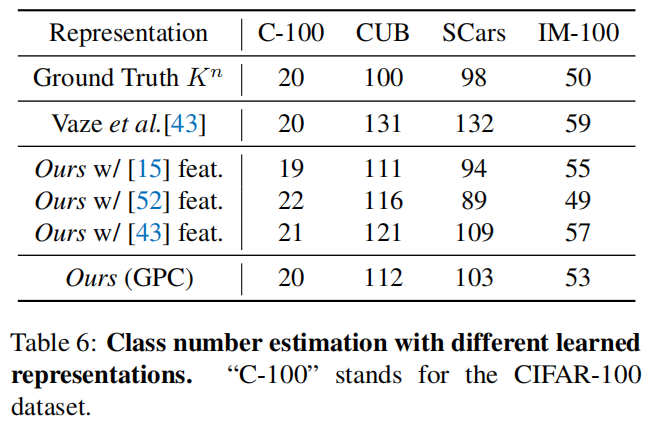
Class number estimation with different representations
将我们的类数量估计方法应用于其他GCD学习到的表征,也可以获得相当好的结果。
- Semi-supervised supervised Learning Gaussian Mixturesemi-supervised supervised learning gaussian semi-supervised supervised laplacian learning semi-supervised supervised semi-supervised regularization adversarial lstm-autoencoder semi-supervised autoencoder ecacl semi-supervised adaptation supervised mixmatch semi-supervised supervised holistic semi-supervised convolutional supervised insights semi-supervised pseudo-label adaptation supervised adaptation semi-supervised supervised标签