20230726
后缀数组
后缀数组 (SA, Suffix Array)
是将字符串的所有后缀排序得到的数组,主要包括两个数组:
\(sa[i]\):将所有后缀按字典序排序后第 \(i\) 小的后缀的开头位置。
\(rk[i]\):表示从第 \(i\) 个字符开始的后缀(我们将它称为后缀 \(i\))的字典序排名
它们满足 \(sa[rk[i]] = rk[sa[i]] = i\)
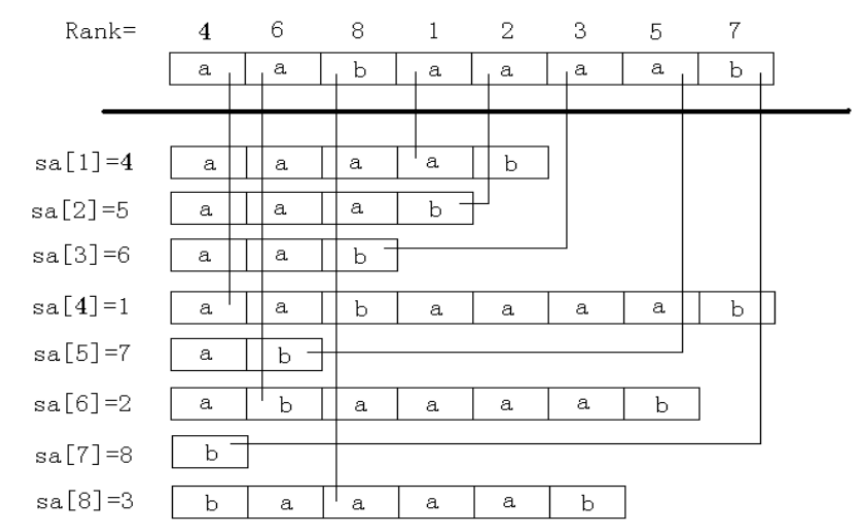
后缀数组能够帮助我们快速解决许多关于子串、后缀的字符串题目
这里介绍后缀数组的 \(O(n log n)\) 倍增求法。
正常比较字符串的字典序需要先比较第一位,再比较第二位 . . . 。
倍增法,顾名思义就是依次比较所有后缀的前 \(k = 1, 2, 4, . . . 2^c\) 位。
首先按照每个后缀的第一个字符对后缀进行排序
这相当于将这个字符串的每个字符进行排序。
接下来考虑已经对 \(k = n\) 排好了序,如何对 \(k = 2n\) 排序:
将每个子串拆分为前 \(k\) 位与第 \(k + 1 ∼ 2k\) 位,如果能分别求出这两部分的排序,
那么对 \(k = 2n\) 排序相当于对这样一个二元组进行双关键字排序。
前 \(k\) 位的排序已知,对于第 \(k + 1 ∼ 2k\) 位,
注意到后缀 \(i\) 的第 \(k + 1 ∼ 2k\) 位,
就是后缀 \(i + k\) 的前 \(k\) 位,
因此这部分的排序可以通过前 \(k\) 位的排序整体移 \(k\) 位 \(O(n)\) 得到。
最后的双关键字排序由于值域只有 \(n\),可以使用基数排序做到 \(O(n)\)。
这样就可以 \(O(n)\) 得到 \(k = 2n\) 的排序
总复杂度 \(O(n log n)\)
代码还是很优美的
P3809 【模板】后缀排序
题目描述
传送门
读入一个长度为 \(n\) 的由大小写英文字母或数字组成的字符串,
请把这个字符串的所有非空后缀按字典序(用 ASCII 数值比较)从小到大排序,
然后按顺序输出后缀的第一个字符在原串中的位置。
位置编号为 \(1\) 到 \(n\)。
用后缀 \(i\) 表示第 \(i\) 位开始的后缀。
\(n \le 10^6\)
Solution
模板题
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,rk[N],sa[N],y[N],c[N];
char s[N];
void getsa(){
m=122;
for(int i=1;i<=n;i++) rk[i]=s[i],c[rk[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=1;i<=n;i++) sa[c[rk[i]]--]=i;
for(int k=1;;k<<=1){
int num=0;
for(int i=n-k+1;i<=n;i++) y[++num]=i;
for(int i=1;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k;
for(int i=1;i<=m;i++) c[i]=0;
for(int i=1;i<=n;i++) c[rk[i]]++;
for(int i=1;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[rk[y[i]]]--]=y[i],y[i]=rk[i];
rk[sa[1]]=num=1;
for(int i=2;i<=n;i++){
if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]) rk[sa[i]]=num;
else rk[sa[i]]=++num;
}m=num;
if(num==n) break;
}
}
int main(){
/*2023.7.26 H_W_Y P3809 【模板】后缀排序 后缀数组*/
scanf("%s",s+1);n=strlen(s+1);
getsa();
for(int i=1;i<=n;i++) printf("%d ",sa[i]);
return 0;
}
最长公共前缀-LCP
定义 \(LCP(i, j)\) 表示后缀 \(sa[i]\) 与后缀 \(sa[j]\) 的最长公共前缀。
首先可以只用考虑 \(i \lt j\) 的情况:
- \(LCP(i, j) = LCP(j, i)\)
- \(LCP(i, i) = n − sa[i] + 1\)
LCP Lemma
\(LCP(i, j) = min(LCP(i, k), LCP(k, j))(1 \le i \le k \le j \le n)\)
证明:
令 \(t = min(LCP(i, k), LCP(k, j))\),
那么 \(LCP(i, k) \ge t, LCP(k, j) \ge t\),
后缀 \(sa[i]\) 前 \(t\) 位 \(= sa[k]\) 前 \(t\) 位 \(= sa[j]\) 的前 \(t\) 位,
故 \(LCP(i, j) \ge t\)。
若 \(LCP(i, j) = q \gt t\),
那么 \(i, j\) 的前 \(q\) 个字符相等,
因为 \(t = min(LCP(i, k), LCP(k, j))\),
所以要么 \(sa[i][t + 1]\)(表示后缀 \(sa[i]\) 的第 \(t + 1\)位)\(\lt sa[k][t + 1]\),
要么 \(sa[k][t + 1] \lt sa[j][t + 1]\),
并且 \(sa[i][t + 1] \le sa[k][t + 1] \le sa[j][t + 1]\),
所以 \(sa[i][t + 1] \ne sa[j][t + 1]\),
与假设矛盾,所以 \(LCP(i, j) = t\)
LCP Theorem
\(LCP(i, j) = min(LCP(k − 1, k)) , k \in (i, j]\)
证明:
由 LCP Lemma:
\(LCP(i, j) = min(LCP(i, i + 1), LCP(i + 1, j)\),
然后继续拆下去即可证明。
height数组
令 \(height[i] = LCP(i, i − 1), height[1] = 0\),
那么求出 height
LCP 就是个区间 min 了
令 \(h[i] = height[rk[i]]\),
于是 \(height[i] = h[sa[i]]\),
对 \(h[i]\),有定理:
\(h[i] \ge h[i − 1] − 1\)
证明:
首先我们假设 \(sa[rk[i] − 1] = j, sa[rk[i − 1] − 1] = k\),
于是 \(h[i] = LCP(j, i), h[i − 1] = LCP(k, i − 1)\),
于是我们只需证明 \(LCP(j, i) \ge LCP(k, i − 1) − 1\)
如果后缀 \(k\) 与后缀 \(i − 1\) 首字母不同,显然成立。
如果后缀 \(k\) 与后缀 \(i − 1\) 首字母相同,
那么分别去掉首字母后得到后缀 \(k + 1\) 与后缀 \(i\),
必有 \(rk[k + 1]\) 也 \(\lt rk[i]\),
于是 \(LCP(k + 1, i) = h[i − 1] − 1\),
对于字符串 \(i\),
所有排名比它靠前的字符串中,
与它相似度最高也就是 LCP 最大的一定是紧挨着它的字符串,即 \(j\),
但我们已知 \(k + 1\) 排在 \(i\) 前面并且
\(LCP(k + 1, i) = h[i − 1] − 1\),
那么必然有
\(LCP(j, i) \ge LCP(k + 1, i) = h[i − 1] − 1\),
即 \(h[i] \ge h[i − 1] + 1\)。