526互联

P8061 [JSOI2016] 炸弹攻击1 - 数据加强版

发布时间 2023-12-01 17:12:17作者: FAKUMARER

P8061 [JSOI2016] 炸弹攻击1 - 数据加强版

第一种情况现有的题解讲的很详细，这里只讨论第二种情况

也就是求 与两圆相切 且 过定点的圆 的方法

并且似乎现有的二分思路不严谨？

先来考虑正常二分的思路

选定 一个点 和 一个圆，二分 增加半径，求出扩张后 新的圆交点，然后与 判断与第二个圆的位置关系

如下图

image

淡灰的圆就是 选定点和选定圆 扩张半径后的圆（后称 扩张圆）

然后取之 交点 为圆心，二分的值为半径，可以得到当前二分的 答案圆

显然，这个答案圆可以保证 经过选定点 且 和选定圆相切

只要得到一个 半径 使得这个答案圆也和 判定圆（第二个建筑）相切，就完了

然后从上图看，此时 判定圆半径 \(r\) + 二分半径 \(Mid\)

是小于 判定圆圆心 到 扩张圆交点 的距离 \(Dis\) 的，从图中情况来看需要增加 \(Mid\)

然后如下

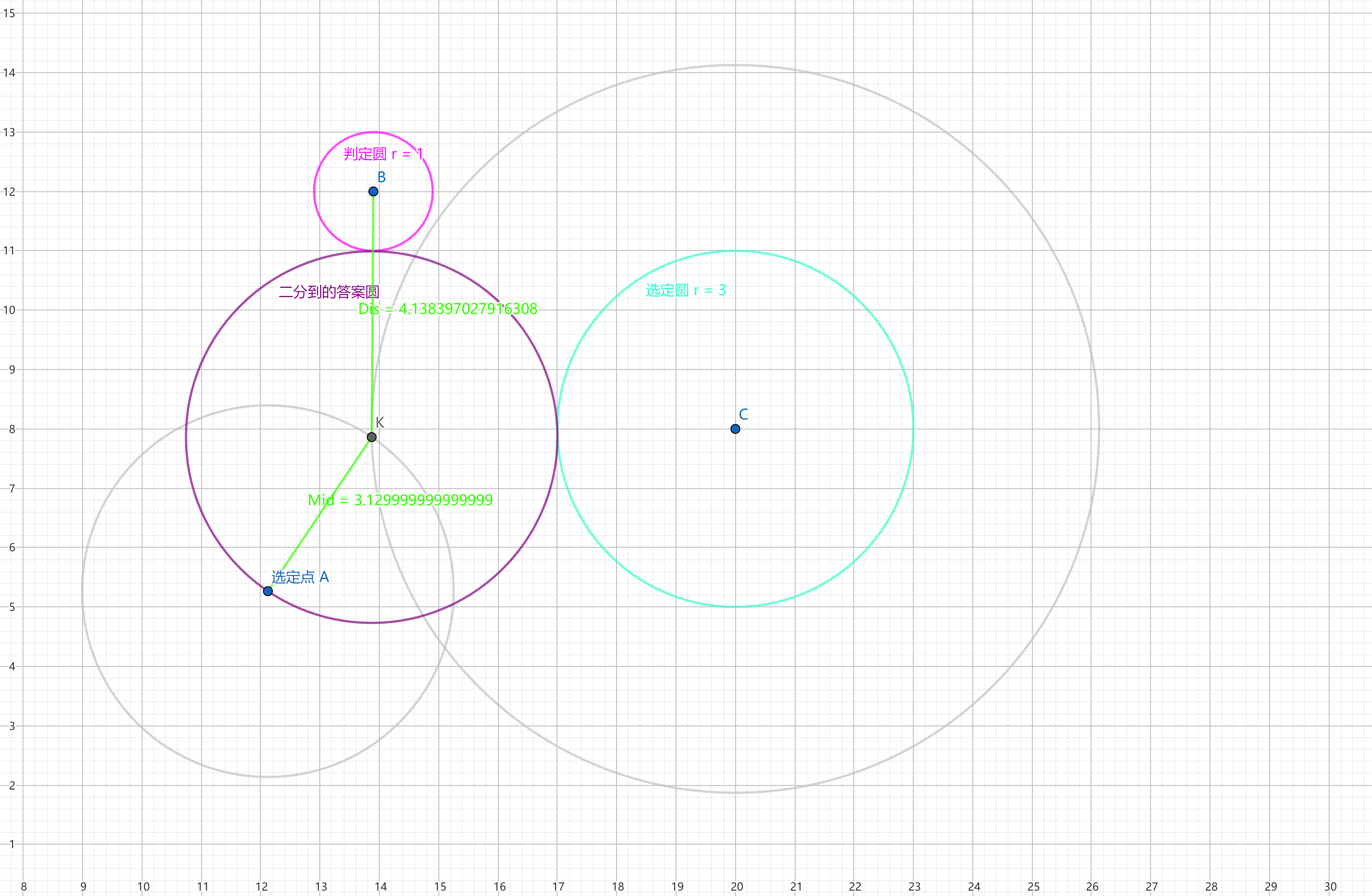
image

成功相切了！（可能图不是很精准，但却是有这个趋势）

于是可以猜 \(Mid\) 和 \(Dis\) 存在单调性关系

即当 \(Mid ~ + ~ r < Dis\) 时，增加 \(Mid\)，反之减少 \(Mid\)

于是二分之后得到答案圆，\(O(M)\) 判断圆中的 敌人，就可以 \(AC\)

但是神秘的是，似乎存在如下反例

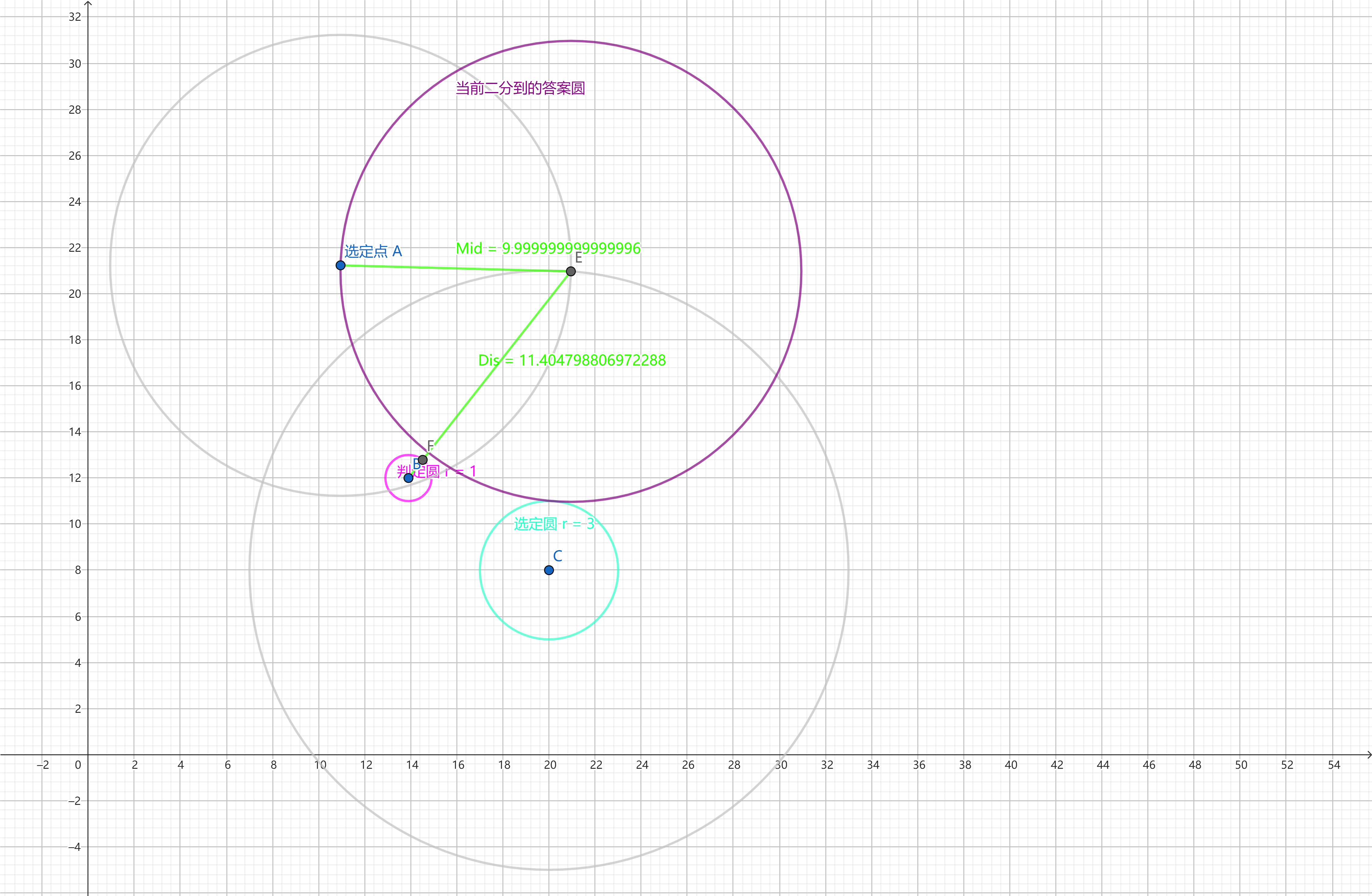
显然在这种时候，\(Mid ~ + ~ r < Dis\)，按理说应该增加 \(Mid\)

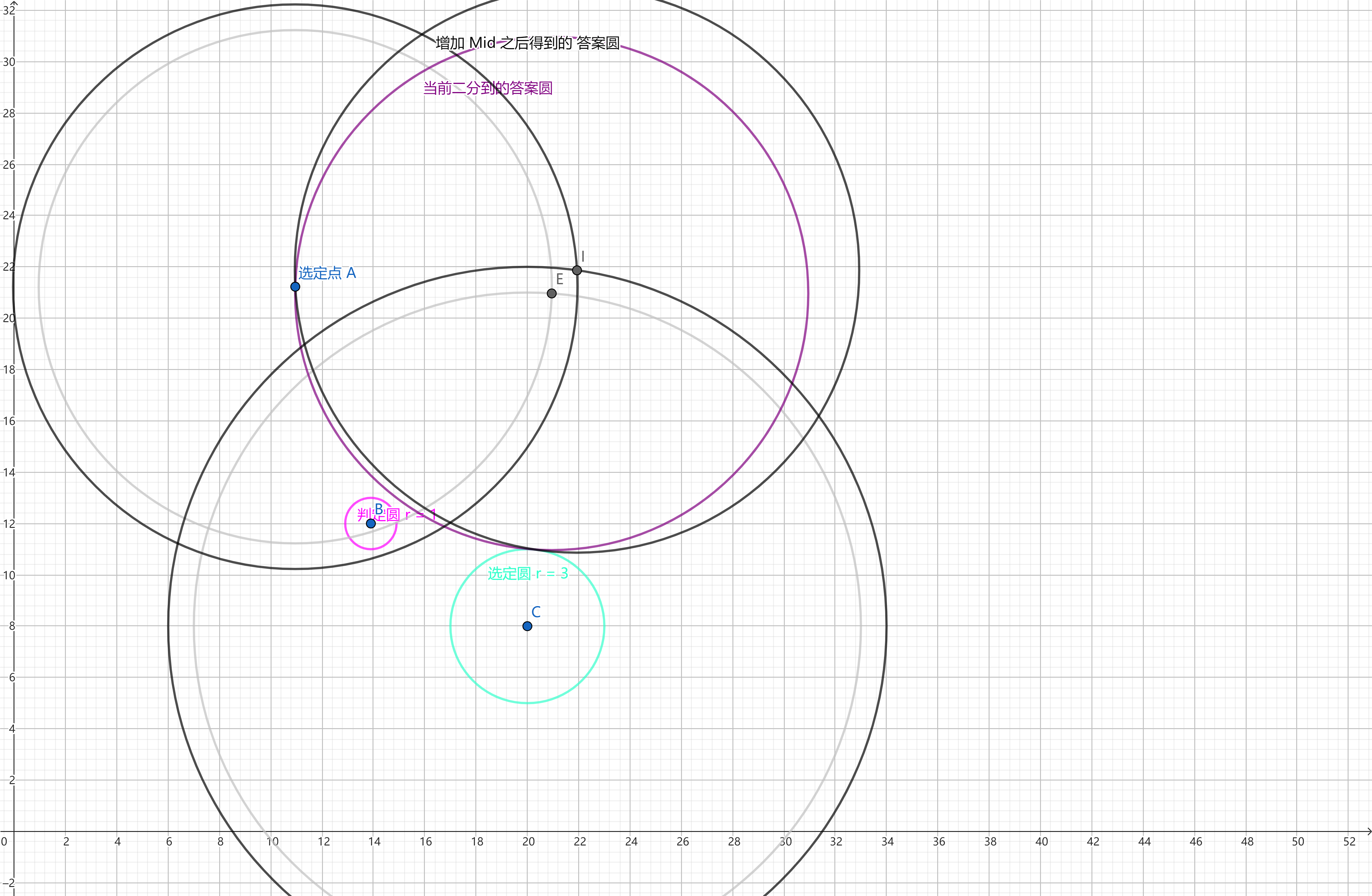
image

上图中新的 答案圆 \(Mid = 11\)

可以发现，新的 答案圆 离判定圆 并没有变近的趋势（\(Dis ~ - ~ Mid\) 的值在扩大）

但尝试将 圆缩小

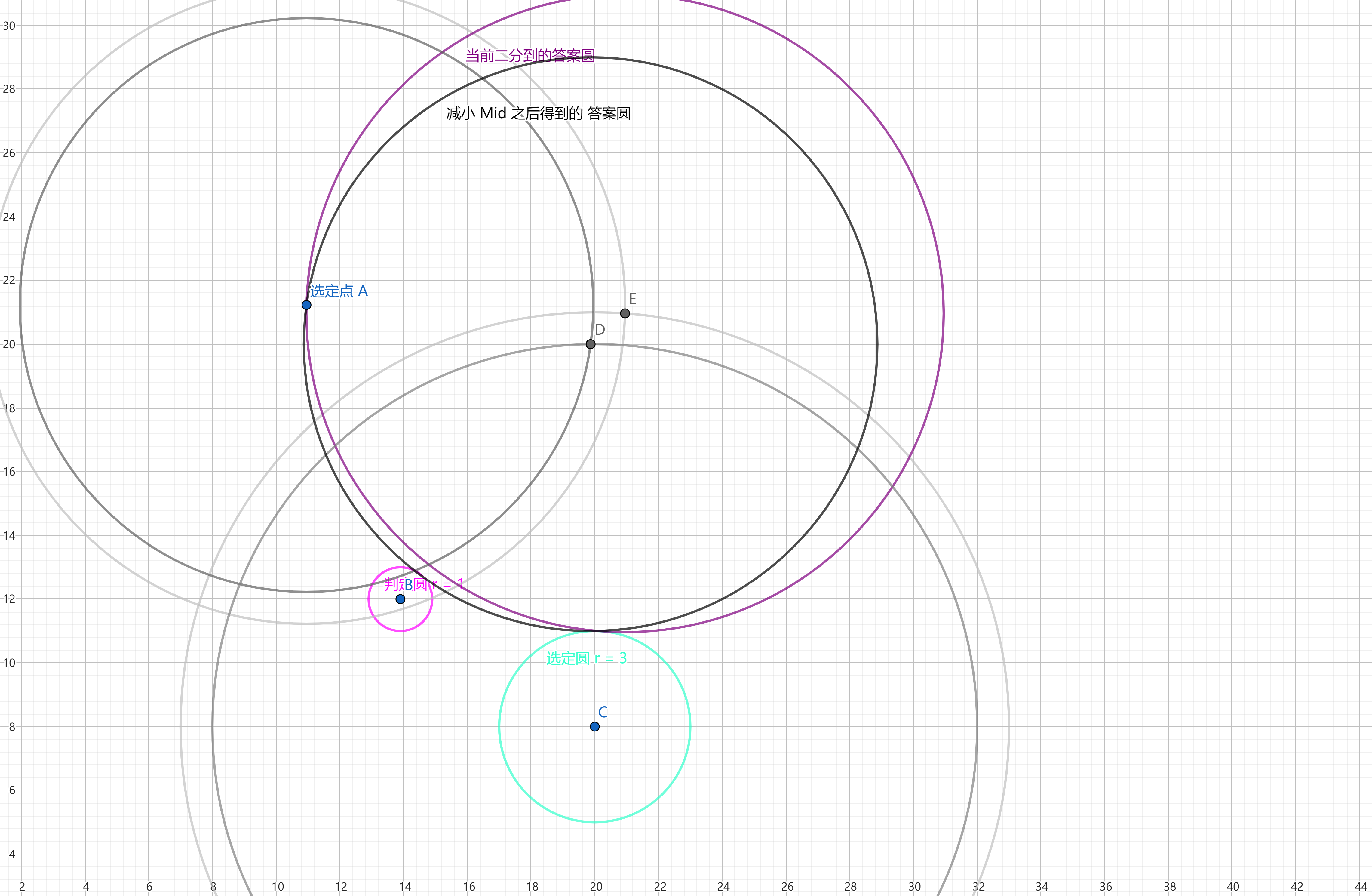
image

上图中新的 答案圆 \(Mid = 9\)

成功相切！

这下十分的 神秘 了，但是似乎 \(Mid\) 与 \(Dis\) 的关系会成一个 单峰函数，可以 三分？

但可能 还有一种方法，可以理论 \(O(1)\) 求到这个 答案圆，但是感觉有 \(INF\) 个细节

可以考虑到 有三个条件就可以确定一个圆，找这三个条件

分别是 经过一定点，与两圆相切，然后列出 三个方程

\[设答案圆圆心 ~ (x,y)，半径~r \\ 切半径为 ~ r_1 ~ 的圆 ~ (x_1, y_1)，半径为 ~ r_2 ~ 的圆 ~ (x_2, y_2)，并过定点 ~ (x_3, y_3) \\ 则有 \\ A:(x - x_1) ^ 2 + (y - y1) ^ 2 = (r + r1) ^ 2 ~~~ (半径和等于距离) \\ B:(x - x_2) ^ 2 + (y - y2) ^ 2 = (r + r2) ^ 2 ~~~ (半径和等于距离) \\ C:(x - x_3) ^ 2 + (y - y_3) ^ 2 = r ^ 2 ~~~ (过定点) \]

似乎很困难，但是好像 二次项可以抵消，于是

\[A - B \\ 2(x_2 - x_1)x + 2(y_2 - y_1)y + 2(r_2 - r_1)r + x_1 ^ 2 - x_2 ^ 2 + y_1 ^ 2 - y_2 ^ 2 + r_2 ^ 2 - r_1 ^ 2 = 0 \\ A - C \\ 2(x_3 - x_1)x + 2(y_3 - y_1)y - 2r_1r + x_1 ^ 2 - x_3 ^ 2 + y_1 ^ 2 - y_3 ^ 2 - r_1 ^ 2 = 0 \\ B - C \\ 2(x_3 - x_2)x + 2(y_3 - y_2)y - 2r_2r + x_2 ^ 2 - x_3 ^ 2 + y_2 ^ 2 - y_3 ^ 2 - r_2 ^ 2 = 0 \]

出现了三个 三元一次 的方程，但是这里注意，显然其中 任意两个可以推出另一个

所以实质上有效方程只有两个，可以 选定主元 并 消掉两个未知数

这里写三个是避免特定情况下 某些方程消元时除数为 0，此时可以换方程消元

然后带入原来的三个方程中 任意一个，可以得 两个解

画图可以发现 几何意义上的解也应该最多为两个

并需要注意

在前面 解一次方程 时，可能就会吧你选定的主元给 直接解出来

（比如选定 \(r\) 为主元，但通过一次方程得到了 \(r\) 的确切值和一个 \(x + y = 10\) 的式子）

这个时候再将 主元 代入二次方程就没有任何意义，应当特判处理

附上我的形式解（很有可能是错的...）

\[设 ~ x = py + qr + w = mr + n ~，~ y = kr + b \\ 则 \\ p = \dfrac{y_1 - y_3}{x_3 - x_1}，q = \dfrac{r_1}{x_3 - x_1}，r = \dfrac{x_3 ^ 2 - x_1 ^ 2 + y_3 ^ 2 - y_1 ^ 2 + r_1 ^ 2}{x_3 - x_1} \\ 然后 \\ k = \dfrac{r_1 - r_2 + x_1q - x_2q}{y_2 - y_1 + x_2p - x_1p}，b = \dfrac{2(x_1 - x_2)w + x_2^2 - x_1^2 + y_2^2 - y_1^2 + r_1^2 - r_2^2}{2(y_2 - y_1 + x_2p - x_1p)} \\ 再然后 \\ m = pk + q，n = pb+w \\ 最终代入 ~ C ~ 式，用求根公式 r = \dfrac{-B ~\pm~ \sqrt{B^2 - 4AC}}{2A} 即可 \\ 其中 \\ A = m ^ 2 + k ^ 2 - 1, B = 2(mn - mx_3 + bk - ky_3), C = n ^ 2 + x_3 ^ 2 + b^2 + y_3^2 - 2nx_3 - 2by_3 \]