3.1 线性回归

回归（regression）是能为一个或多个自变量与因变量之间关系建模的一类方法。在自然科学和社会科学领域，回归经常用来表示输入和输出之间的关系。

3.1.1 线性回归的基本元素

这一部分主要是各种原理及公式，还是需要直接去阅读全文~
总结部分要点如下：

线性回归的前提假设
假设自变量X和因变量y之间的关系是线性的，即y可以表示为X中元素的加权和，这里通常允许包含观测值的一些噪声；
其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。
公式的表示
由于在机器学习领域通常使用的是高纬数据集，建模时使用线性代数表示法会比较方便。
预测值可以从 $ y = w_1x_1 + ...+ w_dx_d+b $ 转为 $ y = Xw+b $ 表示。
损失函数（loss function）
损失函数（loss function）用于量化实际值与预测值间的差距，通常取负数，以符合数值越小损失越小的概念。
梯度下降（gradient descent）
本书中我们用到一种名为梯度下降的方法，这种方法几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。

梯度下降
梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值）关于模型参数的导数（在这里也可以称为梯度）
小批量随机梯度下降（minibatch stochastic gradient descent）
在每次需要计算更新的时候随机抽取一小批样本进行计算，是普通梯度下降的变种，可以减少计算量快速收敛

超参数与调参

超参数（hyperparameter）
可以调整但不在训练过程中更新的参数，如学习率（learning rate）、批量大小（batch size）
调参（hyperparameter tuning）
是选择超参数的过程，超参数通常是我们根据训练迭代结果来调整的，而训练迭代结果是在独立的验证数据集（validation dataset）上评估得到的

泛化（generalization）
线性回归恰好是一个在整个域中只有一个最小值的学习问题。但是对像深度神经网络这样复杂的模型来说，损失平面上通常包含多个最小值。深度学习实践者很少会去花费大力气寻找这样一组参数，使得在训练集上的损失达到最小。
事实上，更难做到的是找到一组参数，这组参数能够在我们从未见过的数据上实现较低的损失，这一挑战被称为泛化（generalization）。
预测（prediction）
给定“已学习”的线性回归模型 $ y = Xw+b $ ，现在我们可以通过房屋面积和房龄来估计一个（未包含在训练数据中的）新房屋价格。
给定特征估计目标的过程通常称为预测（prediction）或推断（inference）。

3.1.2 矢量化加速

在训练模型时，我们经常希望能够同时处理整个小批量的样本。
为了实现这一点，需要我们对计算进行矢量化，从而利用线性代数库，而不是在Python中编写开销高昂的for循环。

n = 10000
a = torch.ones([n])
b = torch.ones([n])
d = a + b  # 使用重载的+运算符来计算按元素的和

矢量化代码通常会带来数量级的加速。这一操作类似于在 pandas 中处理数据时，使用行/列操作的效率远远高于单独对每个单元格进行操作。

3.1.3 正态分布与平方损失

正态分布（normal distribution），也称为高斯分布（Gaussian distribution），若随机变量$x$具有均值$\mu$和方差$\sigma^2$（标准差$\sigma$），其正态分布概率密度函数如下：

\[p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right). \]

均方误差损失函数（简称均方损失）可以用于线性回归的一个原因是：我们假设了观测中包含噪声，其中噪声服从正态分布。
噪声正态分布如下式:

\[y = \mathbf{w}^\top \mathbf{x} + b + \epsilon, \]

其中，$\epsilon \sim \mathcal{N}(0, \sigma^2)$。

因此，我们现在可以写出通过给定的$\mathbf{x}$观测到特定$y$的似然（likelihood）：

\[P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right). \]

现在，根据极大似然估计法，参数$\mathbf{w}$和$b$的最优值是使整个数据集的似然最大的值：

\[P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}). \]

根据极大似然估计法选择的估计量称为极大似然估计量。
虽然使许多指数函数的乘积最大化看起来很困难，但是我们可以在不改变目标的前提下，通过最大化似然对数来简化。由于历史原因，优化通常是说最小化而不是最大化。我们可以改为最小化负对数似然$-\log P(\mathbf y \mid \mathbf X)$。
由此可以得到的数学公式是：

\[-\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2. \]

现在我们只需要假设$\sigma$是某个固定常数就可以忽略第一项，因为第一项不依赖于$\mathbf{w}$和$b$。
现在第二项除了常数$\frac{1}{\sigma^2}$外，其余部分和前面介绍的均方误差是一样的。
幸运的是，上面式子的解并不依赖于$\sigma$。
因此，在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计。

3.1.4 从线性回归到深度网络

我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。

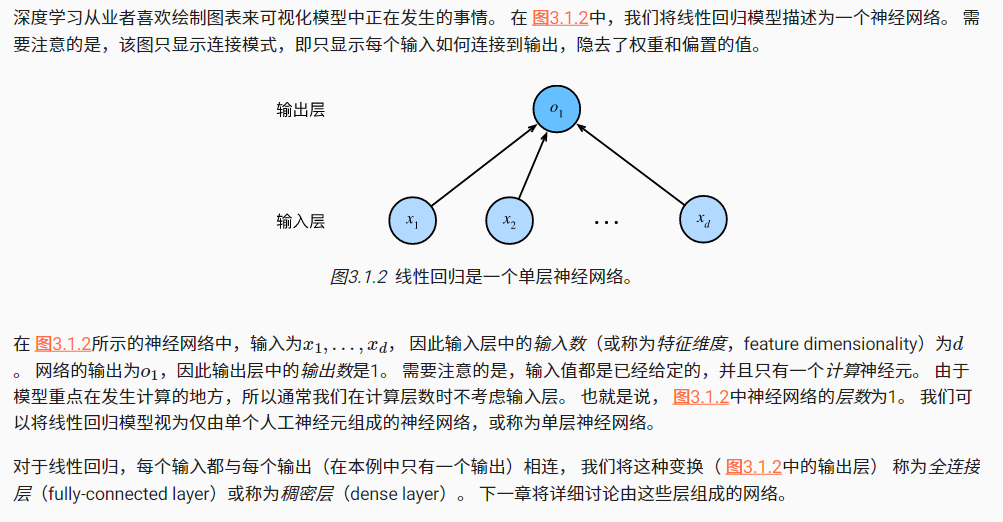
特征维度（feature dimensionality）：输入层中的输入数
层数：由于模型重点在发生计算的地方，所以通常我们在计算层数时不考虑输入层
全连接层（fully-connected layer）/ 稠密层（dense layer）:每个输入都与每个输出（在本例中只有一个输出）相连

3.1.5 总结

当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感。我们援引斯图尔特·罗素和彼得·诺维格在他们的经典人工智能教科书Artificial Intelligence:A Modern Approach :cite:Russell.Norvig.2016中所说的：虽然飞机可能受到鸟类的启发，但几个世纪以来，鸟类学并不是航空创新的主要驱动力。
同样地，如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。