POI 2015

\(\color{royalblue}{P3585\ [POI2015]\ PIE}\)

此题是简单题。

对于方格的一种状态，其中最前排最靠左需要打印的位置，能且只能用印章最前排最靠左的打印位置来打印。不难想到每次找到这样一个未被打印的位置，相对于印章打印位置进行匹配，直接模拟即可。

需要注意的是，印章中只有能打印的位置会造成贡献，所以我们无需考虑不能打印的位置，我们可以将所有能打印位置坐标存下并进行匹配，不合法的情况仅有以下两种：

当前（印章）能打印的位置在边界外。（印出纸张。）
能打印的位置对应方格位置无需打印。（误印。）

\(\color{royalblue}{P3594\ [POI2015]\ WIL}\)

此题是简单题。

直接二分区间长度，判断合法时从左往右枚举区间，对于一个固定的区间显然删除和最大的子区间（长度为 \(d\)）最优，考虑对于前缀和用单调队列维护 \(l\) 至 \(r\) 长度为 \(d\) 子区间和最大值即可。

\(\color{blueviolet}{P3589\ [POI2015]\ KUR}\)

此题是好题。

考虑设小串为 \(t\)，其出现的起始位置为 \(q+1\)（是众多出现位置的其中一个），即使得 \(c_{q+i}=t_i(1\le i\le m)\)，显然有对于 \(q>n-m\) 是不合法的。

我们将题意转化为求合法 \(q\) 的数量，考虑枚举每一个 \(t_i\)。

当 \(t_i=0\) 时，有 \(0\le\left(a(q+i)+b\right)\ \mathrm{mod}\ n<p\)。
当 \(t_i=1\) 时，有 \(p\le\left(a(q+i)+b\right)\ \mathrm{mod}\ n<n\)。

接下来以 \(t_i=0\) 为例，有 \(0\le\left(aq+ai+b\right)\ \mathrm{mod}\ n<p\)，其中 \(ai+b\) 可以看做常数，对于此不等式组可以解出 \(aq\) 的范围，是一或两个区间（因为 \(\mathrm{mod}\ n\) 后求出的区间可看做环上一段区间，可能是 \([0,x],[y,n-1]\) 的形式）。

于是我们得到了 \(m\) 个不等式限制 \(aq\) 的范围（在 \(\mathrm{mod}\ n\) 意义下），题目中给出了 \(a\perp n\) 的条件，所以一个 \(aq\) 也只对应一个 \(q\)。所以我们求所有满足不等式限制的 \(aq\) 个数减去不合法 \(q\) 的个数即可。

考虑到值域很大，所以把每个 \(l,r\) 离散化，差分地对于每个不等式解集区间加，最后前缀和还原，值等于 \(m\) 的位置就是满足不等式的 \(aq\)。至于不合法解，我们考虑预处理 \([n-m+1,n-1]\) 的不合法 \(q\) 对应的 \(aq\)，在统计 \(aq\) 时，减去在其中的不合法值，此操作双指针扫描即可。

\(\color{blueviolet}{P3596\ [POI2015]\ MOD}\)

此题是坏题，它让你输出方案。（代码打了 4.3k，维护直径端点肯定有黑了吧！）

假设固定断掉的边，现在整棵树被此边分割为两棵树，其直径分别为 \(d_1,d_2\)。最长情况显而易见将两直径拼接在一起即可，长度为 \(d_1+d_2+1\)。最短拼接方式一定是取两直径中点连接，长度为 \(\left\lceil\dfrac{d_1}{2}\right\rceil+\left\lceil\dfrac{d_2}{2}\right\rceil+1\)，但考虑到此长度可能短与两树原有直径，所以新直径长度为 \(\max\left\{d_1,d_2,\left\lceil\dfrac{d_1}{2}\right\rceil+\left\lceil\dfrac{d_2}{2}\right\rceil+1\right\}\)。

所以考虑求每个边的贡献，对于一个点（除了根节点）求出其子树内外直径即可，考虑树形 DP。（这里采用一种较为暴力的方法，题解区貌似有更巧妙的方法。）

常见地，我们维护子树内以此节点为一端点的最长、次长、次次长链，子树外向的以此节点为端点的最长链，子树内外直径。转移时注意分讨，考虑到所有转移即可，这道题要求输出方案，所以维护链的时候需要记录两端点。

介绍一个 Trick，在维护最长、次长、次次长数据时，可以采用结构体打包的方式，实现一个小数据结构支持插入值，求除去某一值的最大、次大值。

代码如下，此题中的 \(t1,t2,t3\) 可以换成结构体存储链。

struct Node
{
    int t1,t2,t3;
    void change(int x)
    {
        if(t1<=x)t3=t2,t2=t1,t1=x;
        else if(t2<=x)t3=t2,t2=x;
        else if(t3<=x)t3=x;
        return;
    }
    int query1(int val){if(val==t1)return t2;return t1;}
    int query2(int val){if(val==t1||val==t2)return t3;return t2;}
};

\(\color{blueviolet}{P3586\ [POI2015]\ LOG}\)

此题是好题。

给出结论：去除所有值大于 \(s\) 的数的贡献后，剩余数字和大于等于 \((c-x)\times k\) 时一定有解，其中 \(x\) 是值大于 \(s\) 的数的数量。

这种性质较为显著，手玩并不难发现当满足上述条件时一定存在一种构造使得操作进行完，此处只进行简略讨论。考虑将小于等于 \(s\) 的数从大到小排序，设序列为 \(a\)。将 \(a_2\) 补到 \(a_1\) 上使得 \(a_1\) 等于 \(s\)（若补不齐就用 \(a_3\) 接着补），在剩余 \(a_2\) 的基础上，再用 \(a_3\) 将 \(a_2\) 补齐，每次操作取补齐的最上层。

最后用平衡树维护一下即可，也可考虑离线下来用树状数组或线段树。

\(\color{blueviolet}{P3590\ [POI2015]\ TRZ}\)

此题是神仙思维题。

结论：一定存在一种答案要么左端点在 \(1,2,3\) 三个位置中，要么右端点在 \(n-2,n-1,n\) 三个位置中。

反证法，假设答案为串 \(s\)，其左右三个状态为 \(a\ b\ c\ s\ d\ e\ f\)。

若 \(s\) 中只有一种字符，当其长度一定等于 \(1\) 时，\(a\ b\ c\ s\ d\ e\ f\) 中一定有可以替代 \(s\) 的答案。不等于 \(1\) 时，\(s\) 一定可以向左右扩展至少一次。

若 \(s\) 中不只有一种字符，那我们不妨设 \(|\texttt{B}|>|\texttt{C}|>|\texttt{S}|\)，显然 \(c,d\) 都不是 \(\texttt{B}\)，否则答案一定可以扩展。

再假设 \(c,d\) 中有 \(\texttt{C}\)，设 \(c=\texttt{C}\)。此时 \(c\ s\) 不能被作为答案当且仅当 \(|\texttt{B}|=|\texttt{C}|+1\)。在此基础上，若 \(b,d\) 其中有 \(\texttt{C}\)，那么答案一定可以经过二次扩展使得 \(|\texttt C|'>|\texttt B|\)，所以 \(b,d\) 一定都为 \(\texttt S\)。现在状态来到 \(a\ \texttt S\ \texttt C\ s\ \texttt S\ e\ f\)，考虑 \(s\) 向右扩展的可能性，若 \(e=\texttt C\) 那么 \(\texttt C\ s\ \texttt S\ \texttt C\) 是可以作为答案的，\(e=\texttt B\) 同理，所以有 \(e=\texttt S\)。为了使得 \(s\ \texttt S\ \texttt S\ f\) 不是答案，\(f\) 只能是 \(\texttt C\)。

现在状态来到 \(a\ \texttt S\ \texttt C\ s\ \texttt S\ \texttt S\ \texttt C\)=，为了使得整个串不是答案要求 \(a=\texttt B\)，但此时 \(\texttt B\ \texttt S\ \texttt C\ s\) 是可行答案。

故答案在此假设下一定能扩展，与命题不符。

假设 \(c,d\) 中无 \(\texttt C\)，全为 \(\texttt S\)。考虑 \(\texttt S\ s\) 与 \(\texttt S\ s\ \texttt S\)，它们都不是答案那么一定有 \(|\texttt B|=|\texttt C|+2=|\texttt S|+2\)。考虑 \(b\ \texttt S\ s\ \texttt S\)，它不是答案一定有 \(b=\texttt C\)，同理 \(e=\texttt C\)。现在状态为 \(a\ \texttt C\ \texttt S\ s\ \texttt S\ \texttt C\ f\)，对于 \(s\ \texttt S\ \texttt C\ f\)，它不是答案一定有 \(f=\texttt S\)，同理 \(a=\texttt S\)。

现在状态来到 \(\texttt S\ \texttt C\ \texttt S\ s\ \texttt S\ \texttt C\ \texttt S\)，发现其本身就可以作为答案，与命题不符。

根据以上证明，一个合法的串一定可以一直扩展直到其有一端点在整串两端三个字符内。

暴力枚举左端点和右端点，扫一遍即可。

\(\color{blueviolet}{P3582\ [POI2015]\ KIN}\)

此题是平凡题。

不难想到按照大小关系进行建边，大数字向小数字建边，然后跑拓扑求方案。

但我们发现边的量级很大，考虑优化建图，对于每一个约束条件考虑建出一个超级源点令所有 \(x_i\) 指向它，并令它指向区间内其他点，如下图。

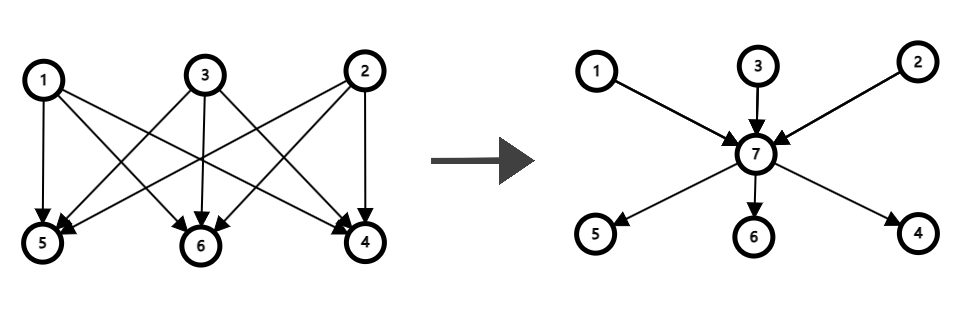
但是边的数量级仍然不小，我们考虑线段树优化建图，把每个超级源点拿到线段树里建边。

拓扑前首先要判环，有环是无解的，其次方案中的数字都不能小于 \(1\)。

\(\color{blueviolet}{P3592\ [POI2015]\ MYJ}\)

此题是好题。

我们只关心 \(c_i\) 的相对关系，所以把 \(c_i\) 离散化后在其上下功夫。

考虑区间 DP，设 \(f_{i,j,k}\) 表示区间 \([i,j]\) 的店，最小价格至少为 \(k\) 的最大收益，考虑枚举断点 \(t\)，有转移：\(f_{i,j,k}=\max\left\{f_{i,t-1,k}+f_{t+1,j,k}+val(i,j,k,t)\right\}\)。

\(val(i,j,k,t)\) 表示区间 \([i,j]\) 内的人，最小值在 \(t\) 处为 \(k\) 产生的贡献。显然可以看出其中包括的人的 \(a_x,b_x\) 一定满足 \(a_x\in[i,t]\and b_x\in[t,j]\)，因为只有他们才能产生贡献，每个人的贡献为 \(k\)，不妨设 \(sum(i,j)\) 表示被包括在区间 \([i,j]\) 中的人的个数，可以表示可以产生贡献的人数 \(sum(i,j)-sum(i,t-1)-sum(t+1,j)\)，故有 \(val(i,j,k,t)=k\times\left(sum(i,j)-sum(i,t-1)-sum(t+1,j)\right)\)。

具体地，考虑转移时 \(k\) 从大（\(c_i\) 最大值）向小枚举，每次加入可以产生贡献的人（\(c_i>=k\)），预处理 \(sum(i,j)\)，于是可以 \(\mathcal O(1)\) 转移。特殊地，考虑 \(f_{i,j,k}=f_{i,j,k+1}\)，显著此层的状态可以继承上一层。

对于方案只需要记录转移过来的层数以及断点即可。

\(\color{blueviolet}{P3587\ [POI2015]\ POD}\)

此题是套路好题。

可以考虑对于每一种颜色单独建立前缀和，即不考虑其他颜色，是这种颜色记 \(1\)，不是记 \(0\)。特殊地，若此位置以及往后没有此颜色，我们把此位置前缀和清 \(0\)（可以考虑是环状结构，所以能造成贡献的只有这种颜色所存在的区间）。对于两个位置是合法的切割点，当且仅当两个位置的所有颜色前缀和值都相等。

发现 \(k\) 是 \(10^6\) 级别的，我们考虑用哈希处理一个位置上的所有颜色前缀和，这样就可以做到 \(\mathcal O(1)\) 判断。

对于方案数，将哈希值排序，对于相等的一段计数即可；对于两段差的最小值，考虑在一段相等的哈希值中按照哈希值位置排序，双指针扫描即可。

\(\color{blueviolet}{P3597\ [POI2015]\ WYC}\)

注意到 \(k\) 是极大的，而且这道题要求我们在图上计路径条数（第 \(k\) 小），\(n\) 又很小，显而易见可以用矩阵乘法维护路径条数（\(mat_{i,j}\) 表示从 \(i\) 到 \(j\) 长度为定值的方案数，\(0\) 为中点起点）。对于边权的处理可以考虑拆点，对于点 \(x\) 拆为 \(x_1,x_2,x_3\) 三个点，顺序连边权为 \(1\) 的有向边，连边时连对应点即可。

考虑求第 \(k\) 小路径，如果一次一次乘显然超时，考虑倍增优化，设矩阵 \(s_i\) 维护长度为 \(2^i\) 的路径条数，这样可以用矩阵相乘拼凑出任意长度路径个数，先倍增到上界，然后从大到小累计答案。

\(\color{blueviolet}{P3591\ [POI2015]\ ODW}\)

此题是平凡题。

考虑根号分治，预处理每个点步幅小于根号的前缀和（从当前节点走到根或走出树），如果步幅小于根号就用我们预处理的前缀和采用类似树上差分的形式解决，如果步幅大于根号则暴力跳转。注意考虑 LCA 是否在路径上。额外地，可以写一个函数处理 \(k\) 级祖先。

\(\color{black}{P3584\ [POI2015]\ LAS}\)

此题是好题。

考虑对每个食物设状态 \(f_{i,0/1/2/3}\) 表示食物没被吃/被左边吃/被右边吃/被两边吃的可行决策点。考虑到本题只有合法与不合法状态，这里 \(f\) 可以恰好记录决策点来记录方案，有值即可行。转移时讨论 \(a_i,a_{i-1}\) 大小关系即可。

\(\color{black}{P3583\ [POI2015]\ KWA}\)

此题是神仙结论题。

打表找规律题，打很多的表，大概 \(10^4\)，发现其中只有 \(31\) 个数不能被表示出来，其中最大的为 \(128\)。另考虑有 \(9945=S(30)=1^2+2^2+\dots+30^2\)，其前面有 \(31\) 个数的 \(w(x)\) 值大于 \(w(9945)\)，并且是 \(w(9945)+1\)。不难想到这 \(31\) 个数就是 \(9945-p\)，\(p\) 是前文提到的不能被表示的数。简单推理若 \(p\) 可以被 \(30\) 以内平方和表示，那么 \(9945-p\) 也是可以的，否则就需要借助 \(31^2\)，我们猜测这 \(31\) 个 \(p\) 就是所有不能被表示的数。

考虑一下解的情况，设当前 \(x=S(i)-p\)（\(i\) 尽可能小）。

若 \(p\) 可以被表示，那么 \(w(x)=i\)。

若 \(p\) 是不可被表示的，那么一定有 \(x=S(i+1)-q\)，\(q\) 是可以被表示的。因为 \(q=S(i+1)-x\) 是极大的，显然不包括在刚才所说的不被表示的数中，所以 \(w(x)=i+1\)。

现在来考虑这道题的解法。我们先预处理一定范围内的 \(w(x)\) 值，若查询范围在此范围内，则直接输出 \(w(n)\) 并计数即可。若不在范围内考虑通过上述讨论递归计算 \(w(n)\)，计数则考虑对于每一个 \(S(i)\) 都有 \(31\) 个超重的数。特殊地，对于 \(S(w(n))-p\le n\) 的超重数需要单独计算累加。

具体地，我们可以预处理 \(10416\) 以内的值，\(10416=S(32)\)，我们通过刚才的推导得到 \(S(32)\sim S(33),S(33)\sim S(34)\dots\)，之间都有 \(31\) 个超重数，对于 \([S(i-1),n]\)（其中 \(i\) 是使得 \(n\le S(i)\) 的最小数）我们考虑枚举 \(S(i)-p\) 判断超重数是否在范围内即可。

\(\color{black}{P3581\ [POI2015]\ CZA}\)

此题是神仙题。

观察到 \(p\) 的范围很小，我们尝试进行分类讨论。

当 \(p=0\)：
显著地，当且仅当 \(n=1\) 时答案为 \(1\)，剩余情况为 \(0\)。

当 \(p=1\)：
同样显著地，此时当且仅当 \(n=1\or(n=2\and k=0)\) 时答案为 \(1\)，剩余情况为 \(0\)。

当 \(p=2\)：
考虑先放置 \(n\)，它两侧只有可能是 \(n-1,n-2\)，\(n-1\) 旁边只有可能放 \(n-3\)，\(n-2\) 旁边只有可能放 \(n-3\)，以此类推，这种情况下只有顺时针逆时针两种情况，构造并判断即可。

当 \(p=3\)：
我们尝试从 \(n\) 至 \(1\) 依次放进环内，考虑当前放置到编号为 \(i\) 的，显然它只能和 \(i+1,i+2,i+3,i-1,i-2,i-3\) 相邻，我们只需要考虑 \(i+1,i+2,i+3\)，它们都在环内，而 \(i-1,i-2,i-3\) 的情况会在放入它们的时候考虑。

我们现在考虑两个问题：

\(i+1,i+2,i+3\) 两两之间可能有已经放入的点，在此种情况中我们无法将 \(i\) 插入到这种位置，因为这显著是不合法的。
当我们放入 \(i\) 后，\(i+3\) 不能和接下来要放入的点相邻，这就意味着 \(i+3\) 一定要紧挨着两边的点，我们需要判断此时 \(i+3\) 的状态。（这种情况会产生上一个问题，可以理解为 \(i+3\) 与两边合并，使这一段不能放置接下来的东西）。

现在给出以下约定方便表述：

\(i+1,i+2\) 之间为位置 \(1\)，\(i+2,i+3\) 之间为位置 \(2\)，\(i+3,i+1\) 之间为位置 \(3\)。
设 DP 状态 \(f_{i,j,st}\) 表示放置完编号 \(i\) 的东西，是否是逆时针（\(j\)），\(i+1,i+2,i+3\) 之间的位置状态为 \(st\)（对位置 \(1,2,3\) 状态进行状压，分别对应 \(1,2,4\)）。
\(\mathrm{sit}(x,y)\) 表示 \(x\) 是否能坐在 \(y\) 右侧，合法为 \(1\)，不合法为 \(0\)。
\(1\in st\) 表示位置 \(1\) 在当前状态中是可行的，其他表达同理。