论文信息

论文标题：Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks
论文作者：Dong-Hyun Lee
论文来源：2013——ICML
论文地址：download
论文代码：download
视屏讲解：click

1 介绍

　　本文提出了一种简单有效的深度神经网络半监督学习方法。本文所提出的网络是在监督方式下同时使用标记和未标记数据进行训练。对于未标记数据，$\text{Pseudo-Label}$ 是选择具有最大预测概率的类，假设他们形如真实标签。

　　伪标签等同于熵正则化，它有利于类之间的低密度分离，这是半监督学习通常假设的先验。

2 方法

　　$\text{Pseudo-Label}$ 模型作为一个简单、有效的半监督学习方法早在 2013年就被提出，其核心思想包括两步：

- 第一步：运用训练好的模型给予无标签数据一个伪标签，可以用概率最高的类别作为无标签数据的伪标签；
- 第二步：运用 $\text{entropy regularization}$ 思想，将无监督数据转为目标函数(Loss)的正则项。实际中，就是将拥有伪标签的无标签数据视为有标签的数据，然后用交叉熵来评估误差大小；

　　目标函数：

　　　　$L=\frac{1}{n} \sum_{m=1}^{n} \sum_{i=1}^{C} L\left(y_{i}^{m}, f_{i}^{m}\right)+\alpha(t) \frac{1}{n^{\prime}} \sum_{m=1}^{n^{\prime}} \sum_{i=1}^{C} L\left(y_{i}^{\prime m}, f_{i}^{\prime m}\right)$

　　其中，左边第一项为交叉熵，用来评估有标签数据的误差。第二项即为 $\text{entropy regularization}$ 项，用来从无标签的数据中获取训练信号；

　　为了平衡有标签数据和无标签数据的信号强度，引入时变参数 $\alpha(t)$，随着训练时间的增加，$\alpha(t)$ 将会从零开始线性增长至某个饱和值。背后的核心想法也很直观，早期模型预测效果不佳，因此 $\text{entropy regularization}$ 产生信号的误差也较大，因而 $\alpha(t)$ 应该从零开始，由小逐渐增大；

　　　　$\alpha(t)=\left\{\begin{array}{ll}0 & t<T_{1} \\\frac{t-T_{1}}{T_{2}-T_{1}} \alpha_{f} & T_{1} \leq t<T_{2} \\\alpha_{f} & T_{2} \leq t\end{array}\right.$

　　　其中，$\alpha_{f}=3$、$T_{1}=100$、$T_{2}=600$。

3 为什么伪标签有效

低密度分离

　　聚类假设指出决策边界应位于低密度区域以提高泛化性能。

熵正则化

　　该方案通过最小化未标记数据的类概率的条件熵来支持类之间的低密度分离，而无需对密度进行任何建模。

　　　　$H\left(y \mid x^{\prime}\right)=-\frac{1}{n^{\prime}} \sum_{m=1}^{n^{\prime}} \sum_{i=1}^{C} P\left(y_{i}^{m}=1 \mid x^{\prime m}\right) \log P\left(y_{i}^{m}=1 \mid x^{\prime m}\right)$

　　熵是类重叠的量度，随着类别重叠的减少，决策边界处的数据点密度会降低。

使用伪标签作为熵正则化进行训练

　　可视化结果：
　　

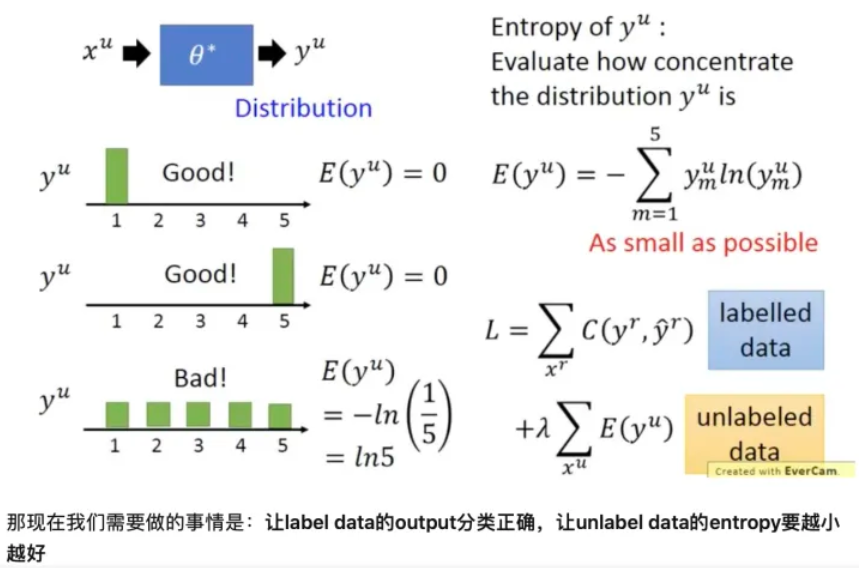
　　在使用神经网络进行分类时, $y^{u}=f_{\theta^{*}}^{*}\left(x^{u}\right)$ , 其中 $y_{u}$ 是 one-hot 编码。现在我们并不限制其必须是某个类别, 而是将其看做1个分布, 我们希望这个分布越集中越好("非黑即白"), 因为分布越集中时它的含义就是样本 $x^{u}$ 属于某类别的概率很大属于其它类别的概率很小。
我们可以使用 Entropy 评估分布 $ y^{\mu}$ 的集中程度 $ E\left(y^{\mu}\right)=-\sum_{m=1}^{5} y_{m}^{\mu} \ln \left(y_{m}^{\mu}\right)$ , 假设是5分类, 其值越小则表示分布 $ y^{\mu}$ 越集中。

　　如下图左侧所示, 上面两个的 $E$为 0 , 所以 $\mathrm{y}$ 的分布很集中; 最后一个 $\mathrm{E}=1 / 5 $, 比上面两个大, 我们只管也可以看出, 他的分布不那么集中。